Sujet de Master 2006-2007
Construction d'une représentation temporellement cohérente d'un modèle animé à partir d'un flux de points 3D
Constructing a temporally coherent representation of an animated model from 3D points flows
 |
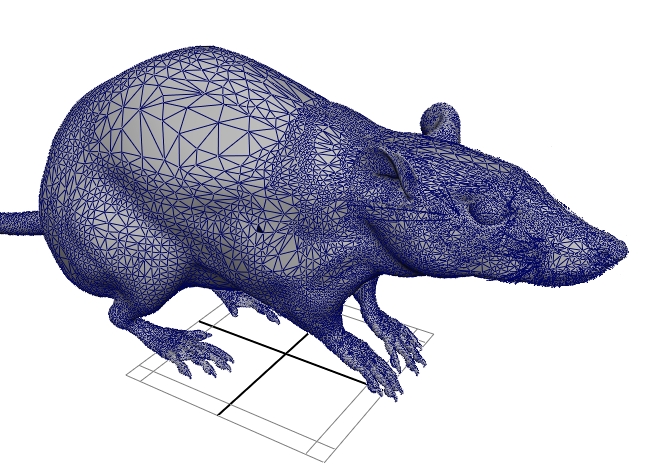 |
| Un nuage de points obtenu par scanner | Modèle maillé (statique) correspondant |
Responsables
| Franck Hétroy | Lionel Revéret |
| GRAVIR/EVASION | GRAVIR/EVASION |
| E-mail : Franck.Hetroy@imag.fr | E-mail : Lionel.Reveret@inrialpes.fr |
| Tél. : 04 76 61 55 04 | Tél. : 04 76 61 52 36 |
Contexte
Note to English-speaking readers: if you want information in English concerning this proposal, please contact me by e-mail.
Dans le cadre du projet ANR Kameleon, réunissant EVASION, le Muséum National d'Histoire Naturelle, le Laboratoire de Neurobiologie des Réseaux Sensorimoteurs de Paris et le Laboratoire de Physiologie et Biomécanique de l'Exercice Musculaire de Rennes, nous disposons de données spatio-temporelles anatomiques, acquises par scanner. Ces données sont représentées sous forme d'un nuage de points, évoluant au cours du temps. Malheureusement, ce nuage de points est triplement bruité :
- tous les points ne correspondent pas au modèle anatomique étudié (par exemple, certains correspondent au sol, à un objet voisin, etc.) ;
- les points acquis sur le modèle peuvent avoir une position géométrique légèrement erronée ;
- le nuage de points n'est pas cohérent d'un instant à un autre : le nombre de points peut varier, tout comme leur position sur le modèle.
Le but de ce stage est de proposer une représentation du
modèle évoluant au cours du temps de manière sémantiquement
cohérente. A priori, cette représentation sera un maillage dynamique, pour
lequel un point représentera toujours la même position sur le modèle, car il
s'agit du type de représentation le plus courant et le plus aisé à visualiser,
mais elle pourra éventuellement être un ensemble de splines caractérisant
chacune une zone du modèle, ou même simplement un ensemble de points
temporellement cohérent.
Il existe dans la littérature de nombreuses méthodes de
reconstruction robuste de surfaces, maillées ou non, à partir d'un nuage de
points 3D [1,3,4,5]. Malheureusement, celles-ci ne reconstruisent qu'une surface
statique, et pour peu que cette surface soit légèrement modifiée, la
reconstruction peut devenir complètement différente. Dans le domaine de la
simulation numérique ont été développées des méthodes de création de maillages
dynamiques, qui suivent l'évolution d'une surface en mouvement, à partir d'un
maillage de la surface à l'état initial [6]. Cependant, ces techniques
nécessitent une première reconstruction de surface statique par un maillage très
dense, et les caractéristiques géométriques de la surface ne sont pas
particulièrement suivies. Les techniques de segmentation de surfaces permettent
elles de partitionner une surface en zones ``homogènes'', éventuellement
délimitées par certaines caractéristiques géométriques précises du modèle, mais
rares sont celles qui travaillent directement sur un nuage de points [2].
Afin de résoudre le problème complexe de reconstruction
temporellement cohérente, on pourra essayer de mêler une méthode robuste (car
nos données sont géométriquement bruitées) de reconstruction de surface et une
méthode de segmentation, s'appuyant par exemple sur la détection de
caractéristiques géométriques. Ainsi, une région de la surface reconstruite
correspondra à chaque instant à la même région du modèle initial. Cette idée
reste néanmoins à étudier de manière rigoureuse, car les caractéristiques
dépendent du modèle et certaines peuvent éventuellement apparaître ou
disparaître lors du mouvement.
Le stagiaire développera en C/C++ et utilisera les
bibliothèques CGAL, GTS ou OpenMesh. L'interface de
visualisation sera réalisée sous OpenGL.
Mots-clés : reconstruction, représentation géométrique, cohérence
temporelle.
Objectifs
- Etudier les techniques existantes de reconstruction d'une part, et de segmentation de surfaces et détection de caractéristiques géométriques d'autre part.
- A partir d'une ou de plusieurs méthodes jugées pertinentes, proposer un algorithme de construction d'une représentation temporellement cohérente du modèle, à partir d'un ensemble de points évoluant au cours du temps.
- Tester et valider cette méthode sur des données fournies par les encadrants.
Références
- R. Allègre, R. Chaine, S. Akkouche. A Dynamic Surface Reconstruction Framework for Large Unstructured Point Sets. Symposium on Point-Based Graphics, 2006.
- R. Chaine. Segmentation d'Ensembles Non Organisés de Points 3D d'une Surface : Propagation Anisotrope d'Etiquettes Basée sur les Graphes. Thèse de doctorat, Université Claude Bernard-Lyon I, 2000.
- T.K. Dey. Curve and Surface Reconstruction: Algorithms with Mathematical Analysis. Cambridge University Press, à paraître le 31 octobre 2006.
- J. Esteve, P. Brunet, A. Vinacua. Approximation of a Cloud of Points by Shrinking a Discrete Membrane. Computer Graphics Forum, 24(4), 2005.
- A. Hornung, L. Kobbelt. Robust Reconstruction of Watertight 3D Models from Non-uniformly Sampled Point Clouds Without Normal Information. Symposium on Geometry Processing, 2006.
- X. Jiao, A. Colombi, X. Ni, J. Hart. Anisotropic Mesh Adaptation for Evolving Triangulated Surfaces. International Meshing Roundtable, 2006.