Master thesis proposal 2008-2009
Non-manifold object classification based on topological properties
 |
 |
Advisors
| Jean-Claude Léon | Franck Hétroy |
| LJK/EVASION | LJK/EVASION |
| E-mail : Jean-Claude.Leon@inpg.fr | E-mail : Franck.Hetroy@imag.fr |
| Tel. : 04 56 52 71 05 | Tel. : 04 76 61 55 04 |
Context
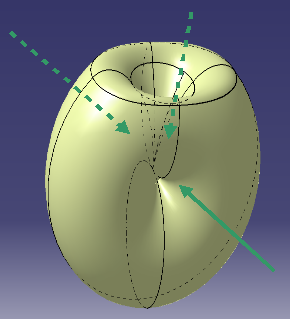
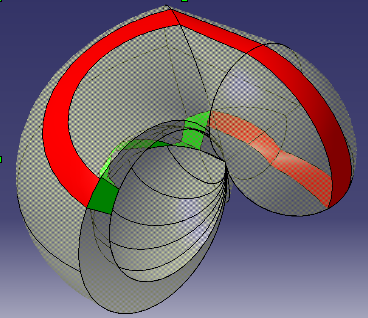
This project is part of a multi-disciplinary and international partnership with the university of Genova, Italy, existing for several years. Its aim is to structure, identify and carry out topological properties describing non-manifold objects, in order to set up new links between these properties and the shape of the corresponding objects. The internship consists in dealing with a specific category of non-manifold objects and characterizing "through holes", in order to create representative subclasses for different categories of "through holes".
Pre-requisites include interest and skills in applied geometry (for instance, MoSIG's second year course "Computational Geometry").
Objectives
For many applications, 3D objects are modeled using volumetric, surfacic and lineic subdomains, each one linked to the others. However, such a layout is often perceived as a set of subdomains, without any link to global topological properties related to the overall shape of the object [1]. Examples of such objects include meshes generated for Finite Element simulations in mechanical engineering, meshes used in architecture, but also leaf, cloth or hair models in computer graphics, for instance.Based on early work identifying representative topological configurations of non-manifold object classes [2, 3], we would like to make the most of some of the defined criteria, in order to both characterize classes of non-manifold objects described by simplicial complexes and define classification algorithms. This work will rely on the decomposition of a non-manifold object into a set of manifold connected components [4]. Studied non-manifold objects will be restricted to objects with 1- or 2-manifold connected components (no 3-manifold, i.e. volumetric, manifold).
Development will be done in C++; the library developed at the university of Genova which decomposes an object into manifold connected components can be used.
Keywords : non-manifold object, topology, mesh.
References
- M. K. Agoston. Computer graphics and geometric modelling: Mathematics. Springer, 2005.
- J-C. Léon, L. de Floriani. Contribution to a taxonomy of non-manifold models based on topological properties. Proceedings of ASME IDETC Int. Conf, 2008.
- C. Crovetto, L. De Floriani, F. Giannini. Form Features in Non-manifold Shapes: A First Classification and Analysis. Eurographics Italian Chapter, 2007.
- A. Hui, L. de Floriani. A two-level topological decomposition for non-manifold simplicial shapes. Solid and Physical Modeling conference, 2007.