Master thesis proposal 2010-2011
Hierarchical segmentation of tree-like structures, with application to medicine and botany
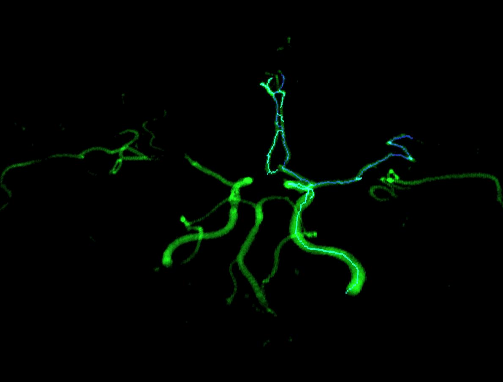 |
 |
| (Already segmented) Cerebral vascular tree | 3D scan of an olive tree |
Advisors
| Franck Hétroy | Michel Desvignes |
| LJK/EVASION | GIPSA-Lab/G-Pi-G |
| E-mail: Franck.Hetroy@grenoble-inp.fr | E-mail: Michel.Desvignes@grenoble-inp.fr |
| Tel. : 04 76 61 55 04 | Tel. : 04 76 82 64 21 |
Context
3D tree-like structures such as the vascular tree in the brain or leafless trees share interesting properties. For instance, they can be represented by 1D data structures such as graphs; branches can also be approximated by cylinders. However, numerical acquisition of real-life tree-like structures alone is often not possible. They must therefore be separated (we use the word segmented) from background or neighboring structures (such as leaves in the botanical context).
Objectives
The goal of this Master project is to propose a unified approach to segment tree-like structures in 3D medical images (IRM; in this case these structures correspond to the cerebral arterial system, see left image above) and in 3D point clouds (which correspond to laser scan acquisitions of real trees from the PlantScan3D project we are involved in, see right image). In both cases, a graph will first be built by connecting neighboring voxels/points and assigning a clever weight to each edge. This weight can be derived from a diffusion distance [CL06]. Then, a graph cut/spectral clustering method will be chosen and adapted to our data. In particular, the tree structure and the fact that branches can be approximated by cylinders need to be taken into account.
Since our data is huge (1 to 3 million points in the case of botanical trees), standard graph cut/spectral clustering techniques cannot be applied as they are. Consequently, in order to fasten the process, the segmentation needs to be hierarchical: the constructed graph will first be simplified several times, and the segmentation process will be initiated at each level using the previous (coarser) one.
As a result, input data should be partitioned into two sets: the voxels/points belonging to the tree structure and voxels/points corresponding to the background or to noise.
Pre-requisites
Required skills include image processing and computer graphics techniques, linear algebra, numerical analysis and statistics. Technical skills include C++ and OpenGL programming. Interest for medicine and botany will be a plus.
Keywords: tree structure, graph cut, spectral clustering, diffusion maps.
References
- [BH10] M. Bronstein, R. Horaud. Diffusion geometry in shape analysis. ECCV tutorial, 2010.
- [CL06] R. Coifman, S. Lafon. Diffusion maps. Applied and Computational Harmonic Analysis, 2006.
- [SM00] J. Shi, J. Malik. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2000.
- [vL07] U. von Luxburg. A tutorial on spectral clustering. Statistics and Computing, 2007.