Projet Image
Optimisation
de la complexité topologique et combinatoire d'isosurfaces
CHAFFARD Vincent
GOSSIAUX Philippe
Sommaire
V. Structures de données
"globales"
VI. Résultats obtenues
VIII. Ce qu'il reste
à
faire
I. Introduction
Le but de ce projet est d’effectuer une variante
du célèbre algorithme du Marching-Cubes
(présenté ci-dessous), d'après l'article "Optimizing the Topological and
Combinatorial Complexity of Isosurfaces" (www.lsi.upc.edu/~pere/papers/Minimac.pdf). Soit O un objet
solide
formé d'un ou
plusieurs composants. Une représentation discrète de O
peut être obtenue en disposant des noeuds sur une grille
régulière en trois dimensions. Les noeuds présents
à l'intérieur de O sont des noeuds noirs, ceux à
l'extérieur de l'objet sont des noeuds blancs. Un tel treillis peut
être obtenue par un procédé de voxélisation
(ce problème est traité dans un autre projet par le
binôme AUJAY-TOURNIER). Notre algorithme prendra donc en
paramètre un fichier décrivant un ensemble de voxels
(c'est à dire ici des cubes), et
devra construire en sortie une surface séparant les noeuds noirs
des noeuds blancs, chaque noeud correspondant au centre des cubes
initiaux. Notre algorithme devra pour construire cette surface
s'appuyer sur des critères globaux tels le genre ou le nombre de
composantes de l'objet.
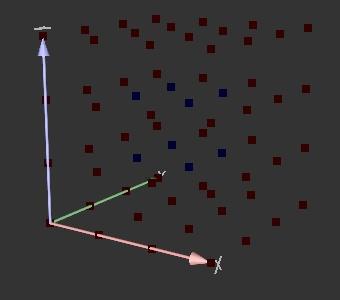
Exemple de voxels: il y a des noeuds bleus (à l'intérieur
de l'objet)
et des noeuds rouges (à l'extérieur)
II. Un algorithme d'extraction de surface: le Marching-Cubes
Le Marching-Cubes donne une solution au
problème d'extraction de surface. En voici le principe; on
découpe l'espace en cube suivant les voxels, tel que chaque
sommet du cube soit un noeud (blanc ou noir).
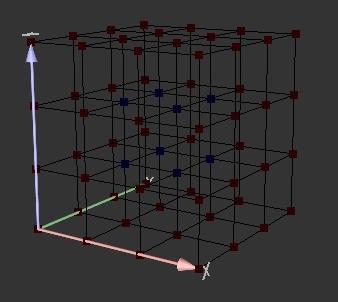
Cubes construits à partir de voxels
Chaque cube ainsi
construit
possède 8 sommets qui sont des noeuds de voxels (blancs ou
noirs). Si l'on considère les 6 faces de chaques cube, on peut
tracer sur chaque face une frontière séparant noeuds
noirs et noeuds blancs, ce qui nous permettra de tracer les
frontières en trois dimensions dans le cube, séparant
noeuds noirs-noeuds blanc;
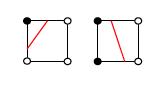
2 exemples de tracé de frontière (en rouge)
Ensuite on trace notre frontière dans le cube
en traçant
plusieurs triangles; un tel procédé s'appelle donc
triangulation.
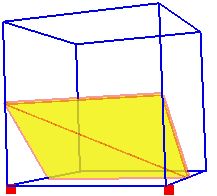
Un exemple simple de triangulation
B.
Limite du Marching-Cubes: cas d'ambiguité
i)
Xface
Le problème de cette algorithme est qu'il y a
différentes
configurations pour un cube qui provoque des ambiguités. Ainsi
si une face se trouve dans la configuration ci-dessous, on peut choisir
deux façons de tracer notre frontière:
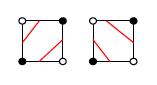
Exemple: une Xface
Il y a 2 façons de tracer une frontière séparant
noeuds noirs/noeuds blancs
(cf en rouge)
Une face présentant une configuration comme
ci-dessus s'appelle
une Xface.
ii)
Xcube
Une autre ambiguité se présente
lorsque le cube se présente sous la configuration ci-dessous; on
peut ou non "tracer un tunnel" entre les deux points de
même couleur:
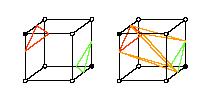
Exemple: un Xcube
Il y a 2 façons de trianguler cette configuration de cube
Un cube présentant une telle configuration
s'appelle un Xcube.
Le choix de couper ou non une Xface, ou de tracer un
tunnel ou non
dans un Xcube, est donc ici un problème local, propre
à chaque cube. L'algorithme du Marching-Cubes utilise pour tous
les cubes une même stratégie et va toujours couper les
Xfaces ou les Xcubes. Cependant, cet algorithme n'est pas envisageable
avec une stratégie globale, c'est à dire une
stratégie où l'on veut prendre en compte les
propriétés de l'objet entier pour tracer la surface
à l'intérieur d'un cube donné..
III. Présentation de
notre algorithme
A. Les stratégies globales pour lever les ambiguités
On propose des stratégie globales pour
optimiser différentes mesures topologiques et combinatoires de
l'isosurface: le nombre de triangles (mesure combinatoire) de
l'isosurface, le genre de
l'isosurface (genre =
nombre de "trou" dans la surface, c'est une mesure topologique) ou le
nombre de composantes de
l'objet (mesure topologique).
B.
Les stratégies pour les Xfaces
Ces différentes stratégies
décident comment tracer la frontière sur une Xface.
Critère 1:
toutes les Xfaces sont "coupées", ie on ne relie pas les deux
noeuds noirs formant la Xface.
Critère 2:
toutes les Xfaces sont "reliées", ie on relie les deux noeuds
noirs formant la Xface.
Critère 3:
si les deux noeuds noirs formant la Xface appartiennent à la
même
composante, on "relie" la Xface,
si les deux noeuds noirs formant la
Xface ne sont pas de même composante, on "coupe" la Xface.
L'algorithme tendra donc dans ce cas à maximiser le nombre de
classes
d'équivalence (classe d'équivalence = une composante),
car lorsque deux noeuds n'appartiennent pas à la même
classe, on ne les relie pas, et donc on ne fusionne pas les
composantes...
Critère
4: si les deux noeuds noirs formant la Xface ne sont
pas de même composante, on "relie" la Xface,
si les deux noeuds noirs formant la
Xface sont de même composante, on "coupe" la Xface.
L'algorihme tendra donc dans ce cas à minimiser le nombre de
classes
d'équivalence, car lorsque deux noeuds
n'appartiennent pas à la même classe, on les relie, et
donc on fusionne les composantes...
C.
Les stratégies pour les Xcubes
Ces différentes stratégies
décident si on trace ou non un tunnel entre les noeuds noirs
d'un Xcube.
Critère A:
pour tous les Xcubes, on ne trace aucun tunnel.
Critère B:
pour tous les Xcubes, on trace toujours un tunnel.
Critère C:
pour tous les Xcube:
un tunnel est tracé si les noeuds noirs du
Xcube appartiennent à la même classe, sinon on ne trace
pas le tunnel.
Ainsi, l'algorithme tendra à maximiser le
nombre de composantes de l'objet.
Critère D:
pour tous les Xcubes:
un tunnel est tracé si les noeuds noirs du
Xcube n'appartiennent pas à la même classe, sinon on trace
le tunnel.
Ainsi, l'algorithme tendra à minimiser le
nombre de composantes de l'objet.
D.
Les différentes décisions combinées
Seules quelques combinaisons de ces
critères sont intéressantes:
1A: on coupe toujours les Xfaces et on
ne
relie aucun tunnel dans les Xcubes. Cette stratégie aura donc
pour effet de maximiser le nombre de
composantes et l'objet sera alors
formé de
plein d'éléments ( nombre de composantes maximal). De
plus, le nombre de
triangles sera minimal (on a
besoin de
moins de triangles pour la triangulation lorsqu'on coupe une Xface ou
un Xcube).
2B: on relie les Xface et on
trace
tous les tunnels dans les Xcubes. Cette stratégie aura donc pour
effet de tout relier dans l'objet, ce qui minimisera alors
le nombre de composante. De
plus, le nombre de triangles sera maximal.
3C: on va maximiser le nombre de
composantes
car dans tous les cas (Xface ou Xcube), on ne va pas chercher à
diminuer le nombre de
composantes. De plus cette
stratégie relie deux isosurfaces si elles appartiennent à
la même composante, ce qui va augmenter le genre.
4D: on va minimiser le nombre de
composantes (cette stratégie relie deux isosurfaces si elles
n'appartiennent pas à la même composante). De plus on ne
relie
pas deux isosurfaces si elles appartiennent à la même
composante, ce qui minimise le genre.
IV.
Implémentation de l'algorithme
Notre algorithme prend en paramètre
le chemin du fichier contenant la description des voxels (un fichier
.vox), et construit en un seul parcours de ce fichier une structure de
donnée décrivant tous les cubes ayant comme sommet les
noeuds des voxels ainsi que la configuration de chaque cube.
Notre algorithme mettra ensuite à jour pour
chaque cube des
booléens permettant de savoir comment on va trianguler chaque
cube par la suite suivant les critères que l'on applique (1A, 3D
ou 4B par exemple...). Cela sera possible en construisant des
structures de données "globales": le Xface propagation graphe et
le Merge tree.
Enfin on effectuera la triangulation suivant les
booléens de
chaque cubes pour afficher notre isosurface.
V. Structures de
données "globales"
A.
Le Xface propagation graph (le graphe de propagation des Xfaces)
Le Xface propagation graph est un outil pour décider du
découpage des Xfaces. On considère le graphe, dans lequel
les cubes qui ont au moins une Xface sont les noeuds et dans lequel
les arêtes représentent un choix possible de
découper une Xface entre les 2 cubes correspondant.
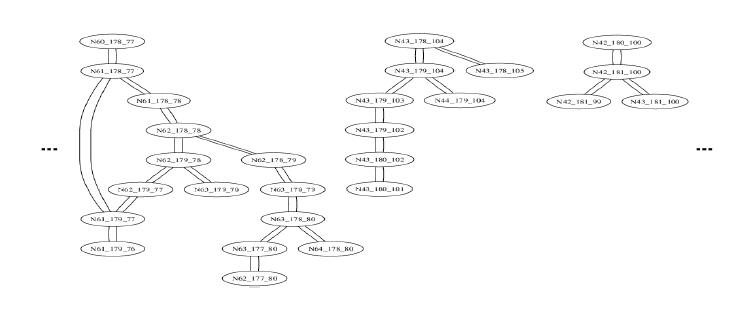
Exemple d'un Xface propagation graph
Voici l'algorithme qui nous a permis de construire le Xface propagation
graph :
Pour
chaque cube c {
Pour
chaque Xface de c {
Si
C a une Xface avec le cube c' {
Si
noeud_graphe(c) n'existe pas le créer;
Si noeud_graphe(c') n'existe pas
le créer;
}
Relier par une arête
noeud_graphe(c) et noeud_graphe(c');
}
}
B.
Le merge tree (l'arbre de fusion)
Cette seconde structure de donnée permet de
connaitre la
connectivité globale des composantes de notre objet. On commence
par construire les racines du merge tree qui sont les ensembles de
classe
d'équivalence, sans regarder les décisions de
découpe des Xfaces et des Xcubes (deux sommets appartiennent
initialement à la même classe d'équivalence si et
seulement si ils appartiennent à la même composante sans
regarder les Xfaces et Xcubes). Ensuite les pères de ces racines
(les classes d'équivalence) dans l'arbre sont des noeuds
représentant la Xface ou le Xcube pouvant faire fusionner ses
deux classes filles...
L'intérêt de cette structure de donnée repose sur
le fait que le nombre de composantes dépend de la
connectivité globale de la surface, et avec une telle structure,
on sait que si on "relie" une Xface, ses deux classes
d'équivalence filles seront fusionnées.
Voici l'algorithme qui nous a permis de construire le merge tree:
(Note: bien sur il faut prendre en compte dans cet algorithme qu'un
noeud peut faire partie de plusieurs cubes)
Initialisations:
classe = 0;
merge tree = vide ;
Pour tous noeuds n {
classe(n)
= -1; //signifie que le noeud n'a pas de classe
}
Pour chaque cube c {
Si
c possède une ou plusieurs ambiguités Xface ou un X cube
à cause de 2 noeuds N1 et N2 {
si N1 n'a pas de classe
{ //classe(N1)==-1
classe =
classe +1 ;
classe(N1) = classe ;
}
si N2 n'a pas de classe { //classe(N2)==-1
classe = classe +1 ;
classe(N2) = classe ;
}
Ajouter au merge tree le "mini-arbre" tel que noeud_merge_tree(C) a
pour fils classe(N1) et classe(N2) ;
}
sinon { //c ne
possède aucune ambiguité
Si
aucun noeud du cube n'a de classe et qu'il existe un noeud noir N parmi
les sommets du cube {
classe
= classe +1 ;
classe(N) = classe ;
}
}
}
Si il existe dans le cube un
noeud N avec classe { //à ce stade toujours vrai
sauf si le cube n'est compos que de noeuds blancs (qui n'ont pas de
classe)
Propager
la classe de N à ses voisins noirs dans le cube ;
Si conflit de classes pour un
noeud du cube {
fusionner
les deux classes conflictuelles en une seule ;
}
}
C.
Algorithme d'application des différentes stratégies
Maintenant que nous avons créé des
structures de données contenant des informations globales, on va
utiliser un algorithme permettant d'appliquer les différentes
stratégies de découpe des Xface et des Xcubes.
Construire
Xface Propagation Graph;
Construire Merge Tree ;
//On convertit le Xface propagation graph en un arbre (non
traité dans notre implémentation)
Si il y a des cycles dans le Xface Graph {
Pour chaque cycles C du graphe faire {
Choisir une Xface du cycle au hasard ;
Couper le cycle C en choisissant une découpe au hasard de la
Xface ;
}
}
//On fixe la
découpe de toutes les Xfaces
Pour toute noeud N du Xface_propagation_graphe {
Fixer la découpe des Xfaces
associée à N(stratégie sur les
Xfaces) ;
Si fusion de deux classes {
Mettre a jour le Merge tree ;
}
}
//pour
chaque Xcube, on décide si on trace un tunnel ou pas
Pour chaque Xcube c faire {
Fixer la
découpe du Xcube (stratégie sur les Xcubes) ;
Mettre a jour Merge tree ;
}
//triangulation finale
Pour chaque cube c {
Trianguler (c)
;
}
VI. Résultats obtenus
Pour plus de clarté dans
nos exemples, on trace en rouge les
cubes qui possèdent des Xfaces et en bleu les cubes qui
possèdent des Xcubes.
L'exemple parfait pour voir la différence entre toutes nos
stratégies est celui d'un cube avec quelques unes de ses
diagonales.
Résultat de la
stratégie 1-A:
Les Xfaces ne sont jamais reliées et les Xcubes ne sont jamais
"reliés".
|
Résultats de la
stratégie 2-B:
Les Xfaces et les Xcubes sont
toujours "reliés".
|
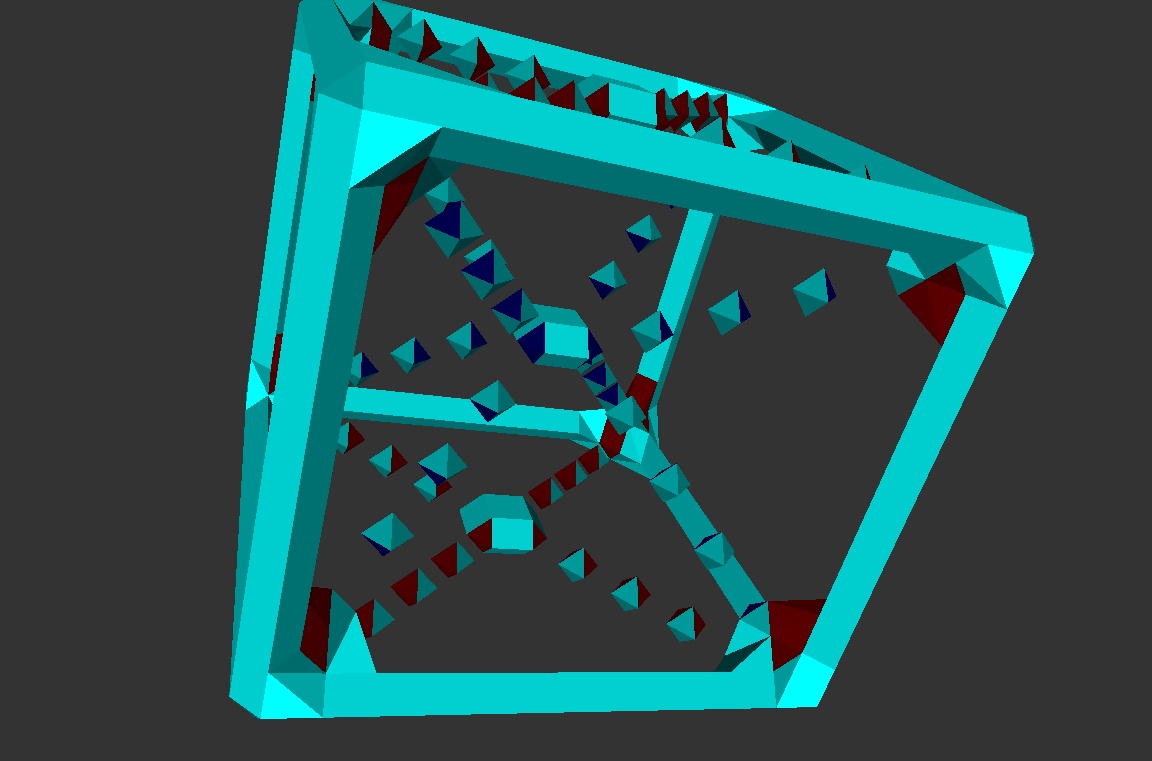
Résultat de la stratgéie 3-C:
Les Xfaces et les Xcubes sont reliés si cela ne fusionne pas
deux composantes
(cf dans les coins du cube...) |
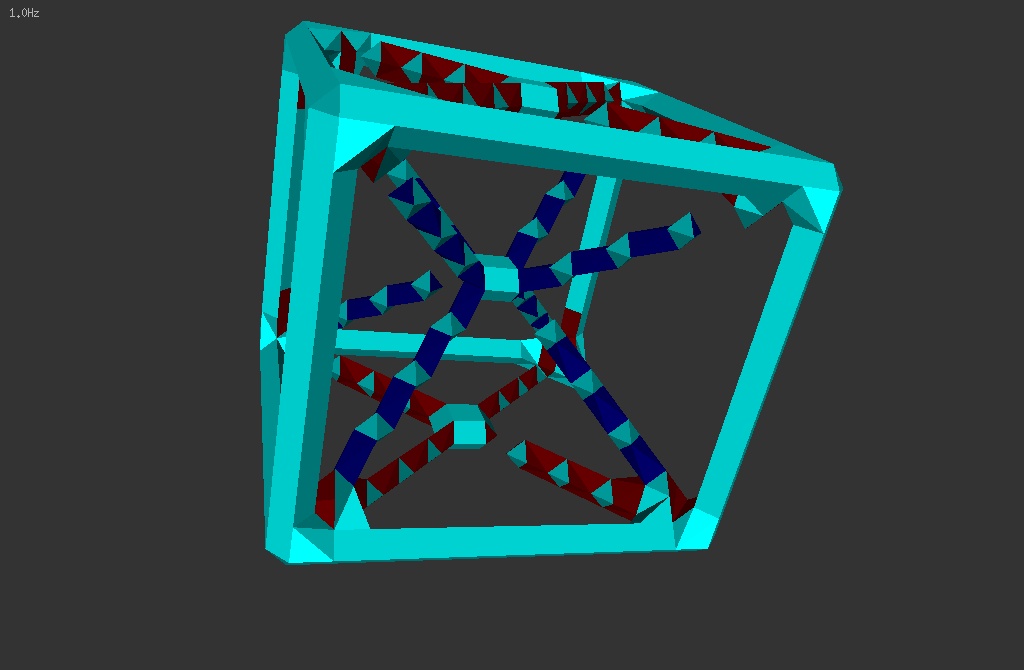
Résultat de la stratégie 4-D:
Les Xfaces et les Xcubes sont reliés si cela fusionne deux
composantes.
On remarque qu'il y a quelques "trous" sur les diagonales: par exemple
en haut à droite on ne relie pas la diagonale au cube car ils
appartiennent
à la même composante... |
Sur cette exemple, les stratégies 1-A et 3-C sont presque
identiques: il y a une Xface dans les coins qui sera reliée ou
non. Mais pour mieux visualiser la différence entre ces 2
stratégies, nous allons utiliser un autre exemple.
On peut aini
appliquer notre algorithme à d'autres
ensembles de
voxels. Pour voir une application de la stratégie 3C, on
construit une
surface à la main (elle ne représente rien de concret...)
qui n'a
qu'une seule composante et qui présente 1 Xface et 2 Xcubes:

Résultat de la stratégie 1-A:
On ne "relie" rien
|
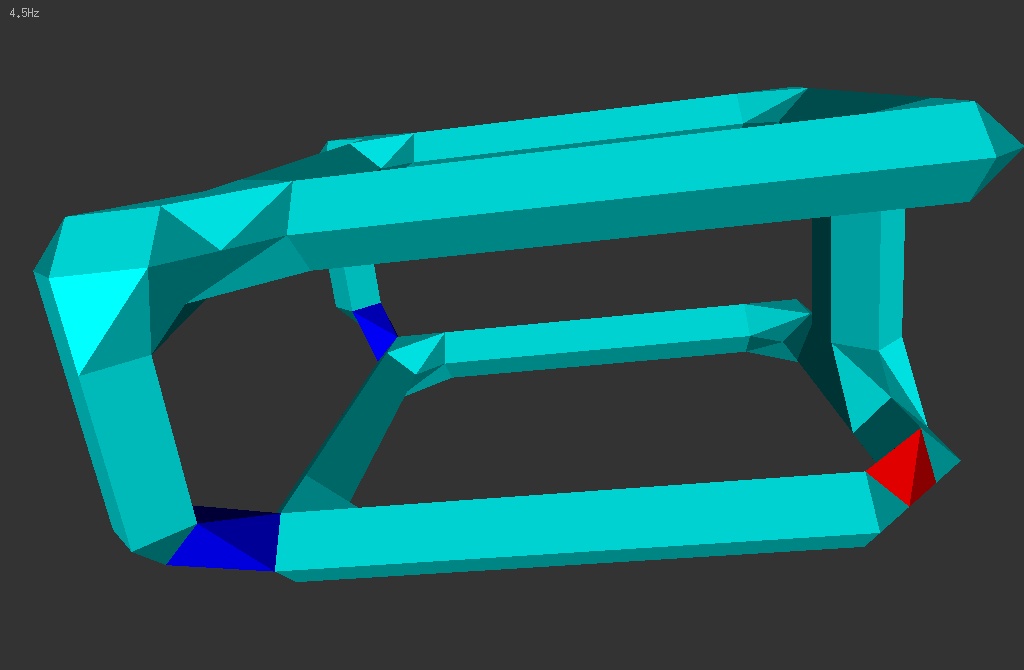
Résultat de la stratégie 3-C:
Puisque l'objet n'a qu'une composante, on "relie" tout
|
Une des raisons d'être de notre algorithme
était d'améliorer le
Marching-Cubes (note: le Marching-Cubes correspond à la
stratégie 1-A
de notre algorithme), en particulier lorsque le Marching-Cubes
"faisait" des trous dans un objet qui n'avait qu'une seule composante.
Ce problème peut quelques fois être résolu en
applicant la stratégie
3-C! En voici quelques exemples:

En applicant le Marching-Cubes,
il y a un trou entre les 2 boules
|

En applicant la stratégie 3-C, on "bouche" le trou !
|
On peut joué sur la connectivité des
éléments avec les différentes stratégies:

Stratégie 1-A:
Les deux "blocs" ne sont pas reliés
|

Stratégie 2-B:
Les deux "blocs" sont reliés par les 3 "tiges"
|

Stratégie 4-D:
Les deux "blocs" sont reliés par une seule "tige"
|
Pour terminer, on met bout à bout le
procédé de voxélisation
(développé par le binome AUJAY-TOURNIER dans un autre
projet). On
obtient ainsi des ensembles de voxels plus gros et représentant
des
objets réels:
Mais sur la plupart de ces exemples, notre algorithme est peu utile car
il n'y a que peu de cubes ambigus:
Le ventre du dinosaure:
il y a peu de cas d'ambiguité: 4 Xfaces (en rouge)
|
Néanmoins sur l'exemple suivant on peut discuter sur le choix de
stratégie:

Zoom sur squelette du pied:
stratégie 4-D
|

Zoom sur squlette du pied:
stratégie 3-C
|
La stratégie 4-D est mieux adaptée dans ce cas, car cela
permet de
mieux séparer les os des doigts de pied. On remarque
néanmoins que ces
os sont reliés à certains endroits non ambigüs. Ceci
est dû à une
voxélisation trop grosse. Cependant une voxélisation plus
petite (cf
quelques images plus haut) n'aurait pas été
intéressante pour nous, car
les os des doigts de pied aurait été trés
nettemment séparés, et il n'y
aurait aucune ambiguité...
VII. Critiques
L'algorithme que nous avons implémenté
nous a donc bien permis de pouvoir construire notre isosurface en
prenant en compte des problèmes globaux. Cependant, nous n'avons
pas exactement respecté sur certains points l'algorithme
proposé.
Tout d'abord, la grand différence se situe au
niveau de la triangulation. Nous avons décidé
d'effectuer la triangulation cube par cube (en prenant un cube dans sa
totalité), ce qui nous a obligé
à traiter toutes les configurations possibles pour un cube. Une
fois que l'on a
déterminé la configuration du cube et que l'on a
fixé l'ambiguité, on trace directement tous les triangles
qui sont à l'intérieur de ce cube là. Il aurait
été peut être plus judicieux de regarder uniquement
les arètes à tracer sur chaque face du cube, et ensuite
de déterminer les triangles de la surface à partir de ces
arêtes tracées. Cela nous aurait évité
d'avoir étudier tous les cas, ce qui est très lourd
à gérer car en plus des 256 configurations, il peut y
avoir (dans les cas ambigus) plusieurs possibilités de
triangulation pour une configuration donnée. L'exemple le plus
frappant est celui où on a 6 Xfaces (ce qui arrive pour 2
configurations) car selon que l'on décide de relier ou de couper
chacune des Xfaces, on aura 2^6=64 possibilités pour une
même configuration.
Ce choix nous avait semblé plus rapide au
départ au niveau implémentation car nous avions
récupéré des tables (lookUpTable.h)
nous donnant la triangulation à effectuer pour
chaque configuration, mais aussi au niveau du temps de calcul.
Cependant, il ne s'est pas avéré aussi judicieux au
final. En effet, nous avons quand même dû refaire toutes
les tables car elles n'étaient pas complétement
adaptées à notre problème. Il a donc fallu
dans un premier temps construire toutes les tables qui permettaient de
gérer toutes des configurations les différents cas,
puis de faire correspondre chaque table avec la stratégie
appliquée.
Ensuite, il existe 2 légères
différences par rapport à l'algorithme proposé
dans l'article "Optimizing the
Topological and Combinatorial Complexity of Isosurfaces", lors
du parcours du graphe de propagation des Xfaces:
- La
première est que nous ne gérons pas (par manque de temps
et non par difficulté...) le cas où il
existe des cycles dans le graphe. Cependant, ce problème n'est
pas très important étant donné que c'est un cas
qui se présente très rarement.
- L'autre différence
est que nous stockons les neuds du graphe dans un tableau et que l'on
parcourt le graphe en partant du 1er noeud stocké dans le
tableau. De son côté, l'algorithme de l'article nous
demandait de parcourir le graphe
en partant d'un noeud ayant une seule Xface. Là encore, cette
différence ne change rien au résultat final puisque ce
choix de commencer par un noeud avec une seule Xface ne se faisait que
pour pouvoir parcourir l'arbre en partant d'une feuille et donc pouvoir
la détruire une fois qu'elle a été traitée.
Ceci explique donc les petites variantes entre
l'algorithme présenté dans la partie V.C
et notre algorithme.
Le dernier point faible de notre
implémentation est son temps de calcul.
Par exemple en salle mac, on met 9 secondes pour obtenir le cheval
définit par 128 noeuds * 128 noeuds * 128 noeuds.
VIII. Ce qu'il reste
à faire
Comme il a déjà été dit
dans la partie
précédente, notre choix pour effectuer la triangulation
nous a empêché de traiter facilement tous les cas. En
effet, on ne gère pas au moment de la triangulation les cubes
qui ont plus de 2 Xfaces. Cela aurait demandé trop de cas
à gérer alors que ce sont des cas qui sont rarement
présents. C'est notamment l'objet de notre 1ère critique
ci-dessus car un autre choix d'implémentation pour la
triangulation
nous aurait peut être permis de gérer plus facilement tous
ces problèmes. Et au final, le temps perdu pour relier toutes
les arêtes entre elles aurait été gagné car
le problème des différentes configurations et
ambiguités aurait été peut être plus simple
à gérer.
Par ailleurs, toujours pour faire face à une
des critiques déjà effectuées, on pourrait
optimiser le code de manière à le rendre plus rapide.
IX. Bilan et organisation
Ce projet nous a donc permis de découvrir un
algorithme intéressant pour calculer des isosurfaces. Cependant,
on a pu se poser la question de l'intérêt de l'algorithme
par rapport au Marching Cubes. En effet, sur des images complexes mais
uniformes comme le dinosaure ou
le taureau, les cas ambigus ne sont pas très nombreux et cet
algorithme
pas très utile. En fait, c'est un algorithme qui sera surtout
intéressant dans des cas précis qui auront beaucoup de
cas ambigus comme le pied ou la main. Il sera aussi très utile
pour toutes les formes qui ont des trous.
Nous avons pu par ailleurs découvrir l'outil
OpenGL pour visualiser notre surface. Cependant, la partie la plus
importante de notre projet a été surtout une partie
algorithme et l'utilisation de structures de données complexes.
Il nous a fallu ainsi créer puis s'habituer à manipuler
les structures de données représentant les cubes par
exemple mais surtout les 2 grosses structures indispensables à
notre algorithme, à savoir le Xface propagation graphe et le
merge tree.
Nous nous sommes donc dans un premier temps habituer
à utiliser OpenGL pour la triangulation et à manipuler
nos stuctures de données. Nous avons donc tout d'abords
codé l'algorithme du Marching Cubes puis dans un deuxième
temps nous nous sommes intéressés à l'algorithme
de l'article et nous avons construit les structures du Xface
propagation graphe et du merge tree pour pouvoir utiliser les
différentes stratégies de l'algorithme.
Ce projet a donc été très
formateur car il nous a permis à la fois de découvrir de
nouveaux outils mais aussi de mener à bien un projet long (1
mois), ce qui nécessite une bonne organisation.