Projet Image
Calcul itératif de géodésiques discrètes
Antoine MELER & Adrien BERNHARDT

Le but de ce projet est d'écrire un programme calculant des géodésiques, c'est-à-dire des plus courts chemins locaux, entre deux sommets d'une surface 3D. Pour cela, il calcule un premier chemin entre les deux sommets, selon un algorithme proposé par Sethian et Kimmel en 1995, qu'il essaie ensuite itérativement d'optimiser. L'algorithme d'optimisation est décrit par Dimas Martinez, Luiz Velho et Paulo C. Carvalho.

Dans le but de nous initier à OpenGL, nous avons choisis d'écrire nous même le programme de rendu 3D à partir de l'excellent tutorial de NeHe. Les surfaces chargées sont au format OFF. Nous nous sommes limité aux surfaces ne possèdant que des triangles.

Description des algorithmes

Création d'un chemin initial

La création d'un chemin initial se fait en deux étapes:

Calcul de la distance de tous les points du maillage par rapport au point P0, d'où partira le chemin. (on utlise la méthode de "Fast Marching")
Construction du chemin en remontant le gradient de la fonction calculée.

La Méthode de "Fast Marching"

La méthode de "Fast Marching" est un algorithme numérique que nous utilisons pour résoudre l'équation Eikonal sur un maillage. (Ce qui était la première application de cette méthode)


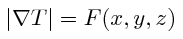
Equation Eikonal

Nous l'utilisons pour définir une fonction de distances entre les points du maillage avec F(x,y,z)=1.

Algorithme

Initialisation:

     Soit P₀ un point du maillage par rapport auquel on veut calculer la distance des autres points.
     On définit: T(P₀) = 0;
     Et pour tout les voisins P de P₀: T(P) = longueur(PP₀).
     P0 est mis dans Accepted et ses voisins dans Narrow band.

Itérations:

Trouver le point P de la liste Narrow band tel que T(P) est minimum.
C'est le Trial.
Mettre le point Trial dans les points Accepted. Le retirer de Narrow band.
Tous les points voisins de Trial qui ne sont pas encore dans Accepted rentrent dans Narrow band.
Pour tous les points P, voisins de Trial dans Narrow band, calculer T(P) en utilisant uniquement les points de Accepted.
Retour à l'étape 1 si Narrow band n'est pas vide.

Propagation de la FMM dans un torus.

En rouge: les points acceptés. (Accepted) En bleu: les points voisins non encore acceptés. (Narrow band)

Contrairement aux méthodes itératives, la FMM est une méthode à passage unique (même si une valeur T(P) est mise à jours plusieurs fois). Une fois qu'une valeur T(P) est acceptée, elle n'est plus recalculée.
Ceci en fait une méthode particulièrement rapide lorsqu'une mise à jour est un calcul complexe.

Le calcul de T(P)

Si l'angle est aigü

Considérons un triangle ABC du maillage pour lequel on suppose connues les valeurs T(A) et T(B) avec de plus T(A) <= T(B) et θ aigü.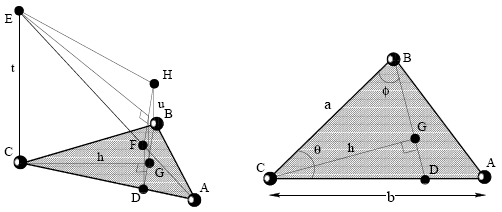

On note u = T(B)-T(A). On cherche à calculer T(C) = T(A) + t avec (t-u)/h = F.
On fixe le module du gradient F à 1 donc: t = h+u.
On peut montrer par des relations géométriques simples que t satisfait l'équation:

( a² + b² - 2ab cosθ ) t² + 2bu( a cosθ - b )t + b² (u² - a² sin²θ ) = 0

La solution doit satisfaire deux conditions:

t > u
a cosθ < h < a/cosθ

Ces conditions garantissent que le front arrive dans le triangle par le côté AB. Kimmel et Sethian démontrent en 1998 que seule la plus grande des deux solutions de l'équation peut satisfaire ces conditions. Si c'est le cas, alors on met à jour T(C) ainsi:

T(C) = min { T(C), t+T(A) }

Si ce n'est pas le cas, alors soit le front se déplace sur une arrète, soit il vient d'une autre direction.
On met alors à jour T(C) ainsi:

T(C) = min { T(C), b+T(A), a+T(B) }

Si le front vient d'une autre direction, alors T(C) ne sera pas changé car il est nécessairement plus petit que b+T(A) et a+T(B).

Si l'angle est obtu

Dans le cas d'un angle aigü, on est sûr que tout front arrivant par le côté d'un triangle va passer par les deux points de ce côté avant d'arriver au troisième. C'est pourquoi, on peut assurer la monotonie en restreignant les mises à jour de T à venir du triangle. Dans le cas ou le point à mettre à jour forme un angle obtu, ce n'est plus vrai. On ne peut donc plus se restreindre à calculer sa valeur T à partir de ses voisins directs.

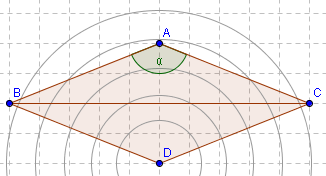
Le front venant de C passe par A avant de passer en B et C.

Une méthode simple pour gérer ce cas est d'ajouter des points de maillage pour découper tous les angles obtus en 2 angles aigüs. Mais nous préférons ne pas modifier le maillage pour que la solution calculée par notre programme reste conforme au fichier entré. Nous choisissons donc d'utiliser l'algorithme proposé par R. Kimmel et J.A. Sethian en 1998. Il consiste en le découpage de l'angle obtu grâce à un point bien choisi du maillage que l'on trouve ainsi:

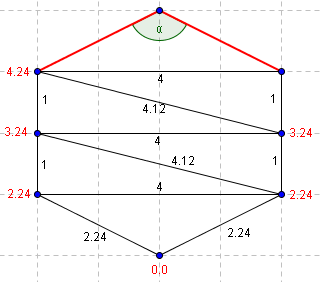
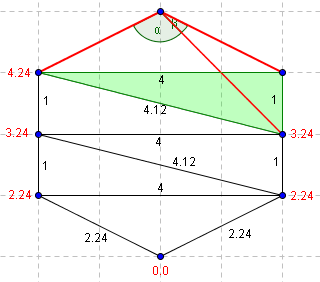
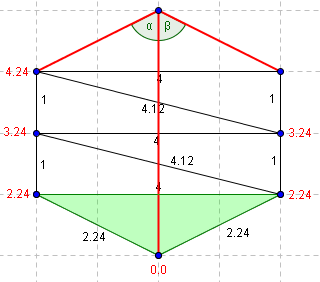
On cherche à déterminer la valeur de T du point du haut. Les valeurs déjas déterminées sont précisées en rouge sur le schéma.


Alpha est obtu, on ne cherche pas à déterminer T à partir des voisins directs du sommet	On se déplace au triangle adjacent (en vert). Le troisième point du triangle adjacent ne permet pas de former deux angles aigüs. (alpha > 90°)

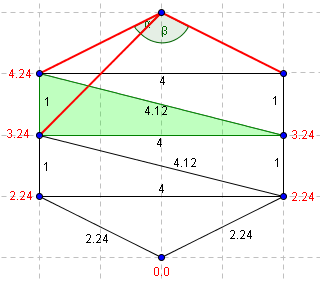
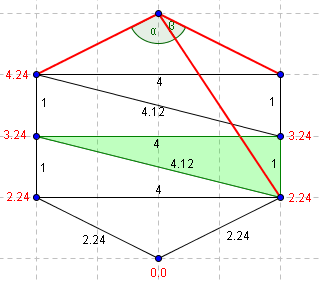
On se déplace au triangle adjacent. Le troisième point du triangle adjacent ne permet pas de former deux angles aigüs. (bêta > 90°)	On se déplace à nouveau. Alpha n'est toujours pas aigü.

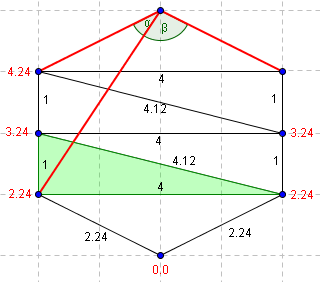
On se déplace à nouveau. Bêta n'est toujours pas aigü.	Le troisième point du triangle adjacent offre deux angles aigüs. On peut donc déterminer la valeur de T à partirs des deux triangles ainsi formés.

La valeur de T déterminée par cette correction est, dans ce cas, rigoureusement égale à la longueur géométrique entre le point du bas et celui du haut (4.0).

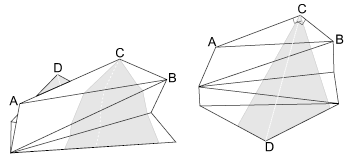
Si le maillage n'est pas plan, il est déplié par rotations successives des triangles selon le segment adjacent avec le triangle précédent.

Maillage avant et après dépliage (ou unfolding).
La zone grisée est la zone dans laquelle doit se trouver D pour que les angles ACD et DCB soient aigüs.

Le problème est que dans certaines configurations, cet algorithme peut tourner longtemps avant de trouver un point permettant de former deux angles aigüs. Dans ce cas, nous faisons le même choix que R. Kimmel et J.A. Sethian: si aucun point n'est trouvé après 10 itérations alors nous mettons à jour la valeur de T de la même façon que dans le cas d'un angle aigü. Dans la majorité des cas, l'erreur engendrée est très faible.

Concervation de la monotonicité

La valeur de T d'un angle obtu n'est pas déterminée par ses voisins directs. Donc cette valeur peut être inférieure à celle de tous les voisins directs du point. Or, il est important pour la suite que la fonction T soit monotone sur le maillage. (en particulier elle ne doit pas contenir de "puits de potentiel") Alors, nous ajoutons le point à partir duquel on a calculé T(P) dans la liste des voisins virtuels de P. Ainsi, tout point P possèdera un voisin (virtuel ou non) de T inférieur.

Construction d'un chemin

Une fois les valeurs de T calculées, l'algorithme de construction d'un chemin initial Γ₀ allant du point A vers B est très simple:

Mettre B dans Γ₀.
P₀=B, i=0
Tant que P_i != A
    P_i+1 = Voisin de P_i avec la plus petite distance T(P_i+1) à A.
    Mettre P_i+1 dans Γ₀.
    i = i+1.

Il s'agit simplement de remonter le gradient de la valeur de T sur le maillage. Cet algorithme fonctionne si la variation de T est monotone sur le maillage.

Lorsque que le voisin de P est virtuel, on ajoute également le mileu des arrètes traversées dans Γ₀.


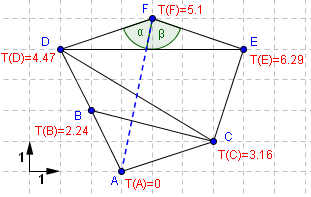
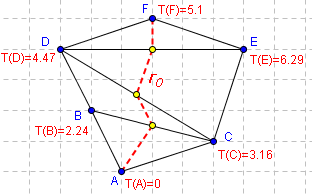
T(F) est déterminé à partir de T(A). A devient un voisin virtuel de F.	Γ₀ passe par le milieu des arrètes entre A et F.

Importance de la monotonicité de T

Sans une liste de voisins virtuels, cet algorithme pourrait boucler infiniment comme dans cet exemple:

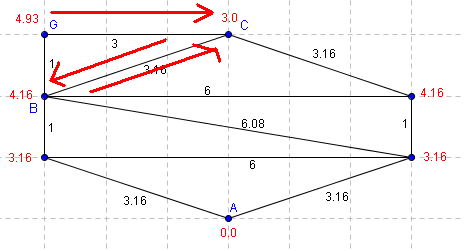
On cherche à construire un chemin de A vers G.
L'algorithme part du point G. Il va en C.
Le voisin de C non virtuel de T minimum est B.
Donc il va en B. Le voisin de B non virtuel de T minimum est C.
Il retourne en C et va boucler ainsi entre B et C...

Optimisation itérative du chemin

Dans cette partie on cherche des chemins nons discrets : les chemins passent par les arêtes des cotés du mech ainsi que par les sommets du mech.

Le but de cette partie est d'optimiser le chemin precedement trouvé afin de le rapprocher point par point d'un minimum local. L'optimisation se fait pour chaque point du chemin et il y a deux cas principaux à considérer. Dans le premier cas le point est sur une arête du mech et dans le second cas le point se trouve sur un sommet du mech.

Cas 1: le point se trouve sur une arête

Cette étape consiste à déplacer le point sur l'arête pour que le chemin soit minimum entre le point précédent et le point suivant. Pour faire cela on déplie la surface et on cherche l'intersection entre la ligne qui joint les points précédent et suivant et l'arête considérée.

Si cette ligne coupe l'arrete alors la nouvelle position de notre point est le point d'intersection.
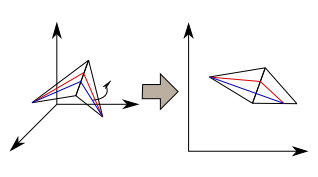
Si cette elle se trouve avant ou après alors la nouvelle position de notre point est le sommet de l'arête le plus proche du point d'intersection.

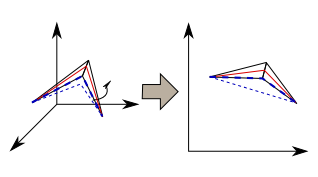
Cette étape est facile à implémenter et ne pose pas de problème dans la pratique.

Cas 2: le point se trouve sur un sommet

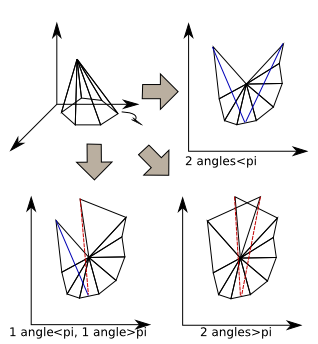
Dans cette étape on cherche à créer un cheminà partir d'un point se trouvant sur un sommet du mech. Pour faire cela on va déplier la surface comme si on la coupait au niveau du point suivant. On obtient alors un patron. Sur ce patron il y a une partie gauche et une partie droite. Si une partie fait un angle inférieur à pi alors on remarque qu'il existe une droite joignant le point précédent et le point suivant; dans ce cas ce chemin est plus court que le chemin précedent. A l'opposé si cet angle est suppérieur ou égal à pi alors un tel chemin n'existe pas. On arrive alors à plusieurs cas :

Dans un premier cas les angles à gauche et à droite sont supérieurs à pi : dans ce cas on ne peut minimiser le chemin actuel ni par la gauche ni par la droite donc notre point est déjà un minimum local : il reste donc à cette place.
Dans un second cas l'un des angles est inférieur à pi et l'autre non. Le seul moyen de minimiser la courbe est de passer du cote ou l'angle est inferieur à pi. Il faut donc passer de ce coté
Dans le dernier cas les deux angles sont inférieurs à pi : dans cette configuration passer à gauche ou à droite nous fait gagner du chemin. Ce pose alors ici un problème de choix. Un premier choix simple est de choisir le coté qui possède l'angle le plus petit. Ce faisant on obtient dans pas mal de cas la meilleur approximation.

Cette partie de l'algorithme pose déjà plus de problèmes :

L'implémentation est faite de cas particuliers pas toujours évidents et nécessite de bonne strutures de données.
Dans le dernier cas le choix de passer à gauche ou à droite est parfois difficille à prendre et d'autres critèrent pourraient se révéler plus efficaces comme par exemple en appliquant notre algorithme une fois aux chemins de gauche et de droite ainsi crée.
Enfin un dernier problème de cette partie est que on passe ici d'un point à un nombre indefini de point mais dans l'état de l'algorithme le contraire n'est pas possible car des points peuvent converger vers un seul et même point mais ce point ne sera jamais atteint et il y a alors bloquage de l'algorithme sur ce point.

Une solution assez simple à ce problème est de définir un critère d'aimantation : c'est à dire que si un point d'une arête est trop proche proportionnellement d'un sommet alors il s'y colle automatiquement. Utiliser cela permet de contourner la convergence lente de l'algorithme au moment de passer un chemin d'un coté à l'autre d'un sommet de mech.

Differrentes implémentations de l'algorithme

il y a plusieurs manières de choisir les sommets que l'on doit traiter ainsi que l'ordre dans lequel les traiter.

Une première méthode la plus simple est la méthode itérative ou l'on parcours tous le chemin et on traite les points du chemin un à un. On construit alors un nouveau chemin avec les points modifiés. Pour augmenter la convergence on peut prendre le dernier point créé comme précédent point pour l'itération suivante.

Une seconde méthode consiste à se doter d'une mesure de l'erreur et à traiter en premier les sommets donc l'erreur élémentaire est la plus grande. On parlera du choix de l'erreur dans la partie suivante. Une fois cette mesure de l'erreur trouvée on peut placer les sommets d'erreur non nulles dans le tas et les traiter dans l'ordre dans lequel ils arrivent en haut du tas. Quand on traite un élément on met à jour son erreur ainsi que l'erreur de ses voisins. Enfin si l'élément présent plusieurs fois dans le tas on ne le traite que celui donc l'erreur donnée est à jour.

Cette dernière implentation fait perdre du temps pour les petits mech car cela necessite plus de tri mais cela s'avère très pratique sur de grands mechs ou une partie du chemin de depart correspond presque avec un minimum local. Dans ce cas cette partie n'a plus besoin d'être traitée alors que d'autres parties peuvent être assez éloignée d'un chemin optimal.

Mesure de l'erreur du chemin

La mesure de l'erreur est assez instinctive. Etant donné que si l'on déplie le patrons d'un chemin optimal on doit obtenir une droite, exception faite des points cols, on peut prendre comme erreur la somme des angles de tous les points du chemin. Pour que cette erreur puisse tendre vers 0 on ne compte pas les points cols. Dans ce cas le chemin tend vers 0.

Implémentation des algorithmes

Représentation du mesh en mémoire

Nous avons écrit une fonction Objet3D* charger_off(char* filename) qui prend en entrée le chemin d'un fichier OFF et retourne un pointeur vers un objet Objet3D. Les variables membres les plus imporatantes de la class Objet3D sont:

	int       nb_points;     // Nombre de points dans le mesh
	int       nb_triangles;  // Nombre de triangles
	Point*    points;        // Tableau des points
	Triangle* triangles;     // Tableau des triangles

Dans le programme, les points et les triangles seront toujours identifés par leur indice dans ces deux tableaux.
La premiere action effectuée par la fonction Objet3D* charger_off(char* filename) est d'allouer puis de remplire ces tableaux en parcourant le fichier OFF.

Pour que la vitesse des algorithmes soit raisonable, on a aussi besoin pour chaque point du mesh de la liste de ses voisins et des faces auxquelles il appartient.
Ces informations sont stockées dans la class Point:

     class Point
     {
     public:
     	float x,y,z;        // Coordonnées du point
     	int* voisins;       // Tableau des points voisins
     	int  nb_voisins;    // Nombre de voisins
     	int* triangles;     // Tableau des faces du point
     	int  nb_triangles;  // Nombre de faces
     ...

La deuxième action de la fonction de chargement du fichier OFF est de créer et remplir ces deux tableaux. Pour ce faire, on parcours une fois l'ensemble des faces. Pour chaque face on ajoute 2 voisins par point, et une face par point (si pas déja présents). Comme on ne sait pas a priori combien chaque point aura de voisins et de faces, on commence à leur allouer des tableaux d'une taille t0. Si, au cours du chargement, on se rend compte que le tableau n'est pas assez grand, on fait:

Allocation d'un nouveau tableau de taille t0*2.
Copie de l'ancien tableau dans le nouveau.
Libération de l'ancien tableau.
Faire pointer l'objet point vers le nouveau tableau.

Ainsi, la place mémoire est suffisante et quasi-minimale sans que l'on ait à faire un parcours préliminaire du mesh pour compter le nombre de voisins et de faces.
Une autre solution serait de faire des listes chainées. Mais nous souhaitons les éviter pour pouvoir accèder à une information par un indice plutôt qu'un parcours de la liste.

En fin, pour l'algorithme d'optimisation du chemin, il est nécessaire de trier les voisins et les faces de chaque points. Cette action est effectuée juste après le chargement du fichier.

La Méthode de "fast marching"

La classe point possède deux membres spécifiques à cette étape:

     	float fmm_t;        // Distance calculée par la FMM
     	int   fmm_status;   // Status du point

fmm_status peut valoir: FMM_ACCEPTED, FMM_NARROWBAND ou FMM_FARAWAY.
L'algorithme de "fast marching" passe son temps à lister les points de la Narrow band. Ces points ne représentent qu'une faible fraction des points du mesh, il est donc important de créer une pile dans laquelle ils seront stockés. Nous utilisons la classe Vector de la STL pour cela.

Implémentation de l'algorithme:

          while(narrowband.size()!=0)
          {
               t_min = INF;
               trial = -1;
     
               /********************************************************
               step 1 :
               Trouver le NARROWBAND de T min, il devient le Trial
               *********************************************************/
     
               for (int pt=0; pt<narrowband.size(); pt++)
               {
                    if (obj->points[narrowband[pt]].fmm_t <= t_min)
                    {
                         trial = narrowband[pt];
                         t_min = obj->points[narrowband[pt]].fmm_t;
                    }
               }
     
               /********************************************************
               step 2 :
               Le Trial devient ACCEPTED
               *********************************************************/
     
               obj->points[trial].setStatus(FMM_ACCEPTED);
     
               /********************************************************
               step 3 :
               Tous les voisins du Trial qui ne sont pas ACCEPTED
               deviennent NARROWBAND
               *********************************************************/
     
               for (int v=0; v<obj->points[trial].nb_voisins; v++)
               {
                    if (obj->points[obj->points[trial].voisins[v]].fmm_status != FMM_ACCEPTED)
                    {
                         obj->points[obj->points[trial].voisins[v]].setStatus(FMM_NARROWBAND);
                    }
               }
     
               /********************************************************
               step 4 :
               Calcul du T de tous les voisins du Trial dans NARROWBAND
               en utilisant uniquement le T des ACCEPTED
               *********************************************************/
     
               for (v=0; v<obj->points[trial].nb_voisins; v++)
               {
                    // on a un voisin v du trial
                    if (obj->points[obj->points[trial].voisins[v]].fmm_status == FMM_NARROWBAND)
                    {
                         // il est dans la Narrow band
                         for (int f=0; f<obj->points[obj->points[trial].voisins[v]].nb_triangles; f++)
                         {
                              // il est dans la face f
                              int p1,p2;
                              for (int u=0; u<3; u++)
                              {
                                   if (obj->triangles[obj->points[obj->points[trial].voisins[v]].triangles[f]].points[u] != obj->points[trial].voisins[v])
                                   {
                                        p2 = p1;
                                        p1 = obj->triangles[obj->points[obj->points[trial].voisins[v]].triangles[f]].points[u];
                                   }
                              }
                              // p1 et p2 sont les deux autres points de la face f
                              calculer_T(obj->points[trial].voisins[v], p1, p2);
                         }
                    }
               }
          }

La fonction calculer_T(p,p1,p2) met à jour le membre fmm_t du point p à partir des points p1 et p2.

Si M est le nombre de points moyen dans la Narrow band, et N le nombre total de points de la surface, le complexité de cette implémentation est O(NM). M dépend fortement de la surface mais il est souvent d'ordre N^1/2.

Il est à noter que l'on peut se contenter d'arrèter l'algorithme lorsque l'on a accepté le point positionnant la fin du chemin.

Optimisation du chemin

La fonction d'itération se présente comme il suit :

Implémentation de l'algorithme:


   if(gamma->size()>0)
      pt_fin = new PointChemin(*(*gamma)[0]);
      gamma_suivant->push_back(pt_fin);
   if(gamma->size()>2){
      aimante((*gamma)[1],aimantation);
      for(int p=0; p<(int)gamma->size()-2;p++){

         aimante((*gamma)[p+2],aimantation);
         /**
          * Si les trois points appartiennent au même triangle alors on supprime le point du milieu
          */
         
         /* code pour supprimer le point et continuer */

         if((*gamma)[p+1]->isVertex()){
         /* code pour traiter le cas deux de l'algorithme */
         
         ....

         } else {

         /* code pour traiter le cas un de l'algorithme */

            PointChemin pcentre = PointChemin((*gamma)[p+1]->getP1());
            PointChemin pmilieu = PointChemin((*gamma)[p+1]->getP2());

            float coefficient = getCoefFromPoints(&pcentre,pt_fin,(*gamma)[p+2],&pmilieu,obj);
            pt_fin = new PointChemin((*gamma)[p+1]->getP1(),(*gamma)[p+1]->getP2(),coefficient);
            gamma_suivant->push_back(pt_fin);

         }
      }
   }
   if(gamma->size()>1){
      pt_fin = new PointChemin(*(*gamma)[gamma->size()-1]);
      gamma_suivant->push_back(pt_fin);
   }

On s'arrange ainsi pour travailler avec le précédent point calculer et améliorer ainsi la convergence de l'algorithme.

Analyse des résulatts obtenus

Quelques chemins initiaux obtenus

Les sommets du maillage faisant partie du chemin sont en vert et le chemin est dessiné en ligne blanche. On voit sur la première image que le chemin passe parfois par le milieu d'une arrète, du fait de la présence d'angles obtus (on le voit par les coupures dans la bande verte).

Quelques chemins finaux obtenus

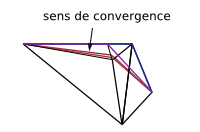
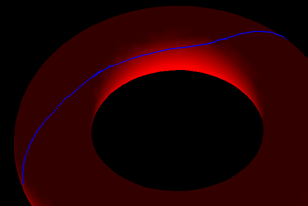
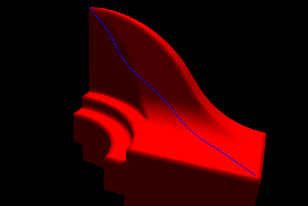
Convergence du chemin corrigé vers le chemin optimal

En rouge: chemin initial. En bleu: chemin corrigé itérativement.

Avantages de la FMM par rapport à l'algorithme de Dijkstra

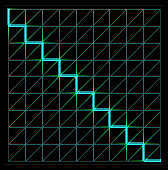
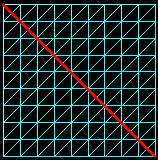
Lorsque l'algorithme de Dijkstra évalue les distances entre les points, il se contente de sommer des longueurs d'arrètes. Or, les distances calculées par la FMM sont plus prochent des distances réelles des points. Donc le chemin résultant est plus proche du chemin optimisé.

Exemple de résultat avec les 2 algorithmes

Chemin obtenu par l'algorithme de Dijkstra	Chemin (de même longueur) obtenu par notre programme	Chemin que l'on souhaite obtenir après optimisation

Inconvénients de l'algorithme de construction du chemin

Le chemin obtenu n'est pas toujours le meilleur. Considérons cet exemple:

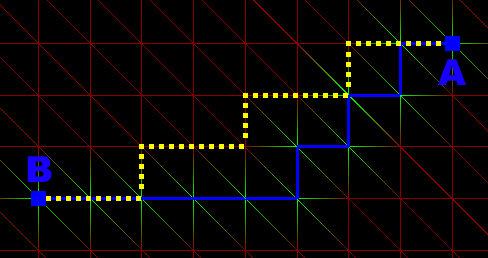
Bleu: chemin calculé par le programme.
Pointillés jaunes: chemin dont la vergence serait plus rapide.

L'algorithme commence à construire le chemin à partir du point B. Tant qu'il n'est pas à 45° de A il se rapproche plus de A en ce déplaçant à droite qu'en haut. Donc il va se déporter vers la droite avant de commencer à monter. Cela crée un chemin qui peut s'écarter très loin du chemin optimal.

On peut aussi voir sur cet exemple que l'algorithme n'est pas adapté à un maillage irrégulier (présentant des segments beaucoup plus longs que les autres).

Rouge: chemin calculé par le programme entre A et D.
Il existait un chemin direct.

En B, l'algorithme a le choix entre 2 points. Il choisit de passer par E, qui est plus proche que C de A.

Ces deux inconvenients sont dûs au caractère fortement discret de la construction du chemin initial.

Amélioration

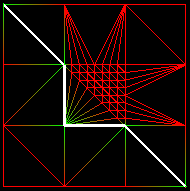
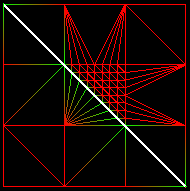
Afin de corriger le problème des maillages irréguliers, nous proposons une amélioration de l'algorithme de construction du chemin. Au lieu de prendre le voisin P_i+1 tel que T(P_i+1) est minimum, nous prenons P_i+1 tel que [T(P_i)-T(P_i+1)]/P_iP_i+1 est maximum. Ainsi, l'algorithme va plutôt chercher à ce déplacer dans la bonne direction que le plus vite possible.
Le résultat est positif:


Chemin obtenu en choisissant P_i+1 tel que T(P_i+1) est minimum.	Chemin obtenu en choisissant P_i+1 tel que [T(P_i)-T(P_i+1)]/P_iP_i+1 est maximum.

Analyse de l'erreur

Nous utilisons des maillages 2D pour mesurer l'erreur entre les valeurs de T calculées et les distances réelles entre les points. Dans le cadre de ce projet, nous utilisons la méthode de "fast marching" avec une source ponctuelle. Donc, le front de l'onde qui se propage possède une forte courbure près de la source, ce qui n'est pas très bien géré par notre calcul de T qui suppose un front droit à l'échelle d'un triangle. C'est la cause des erreurs dans le calcul de T.
Quelques résultats obtenus:
Plus un point est rouge, plus l'erreur y est importante, relativement à l'erreur maximale sur l'ensemble du maillage.
Les deux maillages utilisés on les même dimensions (80x60 de longueur), le même nombre de points et de triangles.
La distance est calculée par rapport au centre du maillage.

Maillage sans angle obtu.	Maillage avec angles obtus.	Même maillage en traitant les angles obtus comme des angles aigüs.

Norme infinie de l'erreur: 1.33 Norme 2 de l'erreur: 73100	Norme infinie de l'erreur: 1.26 Norme 2 de l'erreur: 66000	Norme infinie de l'erreur: 4.90 Norme 2 de l'erreur: 66000

Sur ces maillages, la patch pour mieux gérer les angles obtus permet donc de réduire considérablement la valeur maximale de l'erreur. L'erreur maximale n'est pas très importante compte tenu des dimensions. Pour donner une idée, 1.3/30 = 4.3% . Mais par contre, les variations de l'erreur sont assez importantes. Des points dont l'erreur est nulle sont quasiment voisins de points dont l'erreur est maximale, ce qui peut produire des chemins inatendus.

Avantages de l'algorithme d'optimisation du chemin

Dans l'ensemble le redressement du premier chemin se fait assez bien et en baissant l'erreur recherchée on trouve un chemin tout à fait cohérant qui redresse bien les écarts du premier algorithme.

Quand on a chemin qui part dans tous les sens alors ce chemin va tendre assez vite vers une bonne solution et l'erreur va donc rapidement tendre vers zero au debut.

De plus cet algo n'est vraiment pas optimisé et on pourrait facillement obtenir un algorithme qui converge plus rapidement en considérant moins de points lors de l'optimisation : par exemple une suite de points qui ont un sommet en commun empèche une convergence rapide car cela rapproche les points, de plusles données du premier et du dernier points nous suffisent à retrouver tous les autres points entre c'est deux point donc il y a je pense une bonne amélioration à faire ici.

Enfin une autre possibilité est de faire une aimantation adaptative en fonction de l'erreur restante. Si l'erreur est grande on choisi une aimantation grande ce qui permet de déplacer le chemin rapidement sur des grandes distances. Et quand l'erreur diminue on diminue l'aimantation pour avoir alors un chemin plus fin.

Inconvénients de l'algorithme d'optimisation du chemin

Cet algorithme ne fournit en aucun cas le chemin le plus court entre deux points, il fournis uniquement un minimum local
Dans le cas d'une courbure longue de légère l'algorithme va prendre beaucoup de temp à corriger l'erreur, et cela même dans le cas du tas car les erreurs ont toutes le même ordre

Performances

Nous effectuons des tests de performance sur un PC possèdant un processeur centrino à 1.73 GHz, 1 Go de mémoire vive et une carte 3D à 128 Mo.

Temps de calcul de la FMM

Temps mis sur différentes formes


Points - Faces:	505 - 968	1 572 - 3 152	4 245 - 8 490	6 475 - 12 946
Temps de la FMM:	78 ms	172 ms	531 ms	782 ms


Points - Faces:	12 358 - 24 860	48 485 - 96 966	50 184 - 100 400	100 000 - 199 114
Temps de la FMM:	2 063 ms	6 172 ms	9 500 ms	14 625 ms

Traitement des angles obtus

Pour évaluer le malus de temps engendré par le traitement des angles obtus, nous créons deux surfaces de 10000 points et 19602 faces. Une des deux est parfaitement régulière, et ne possède aucun angle obtu. L'autre est identique mais avec un "bruit" dans la position des sommets, créant une grande quantité d'angles obtus (puisqu'un angle à 90° sur deux devient obtu).


Maillage sans angle obtu Temps de la FMM: 125 ms	Maillage avec des angles obtus Temps de la FMM: 453 ms

Le traitement des angles obtus augmente donc significativement le temps d'une mise à jour de T(P) et donc de la FMM.

A propos du programme

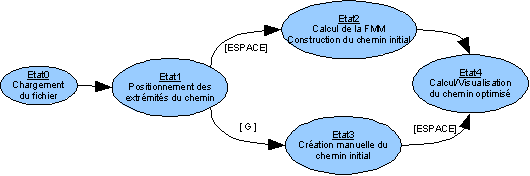
Notre programme ne possède malheureusement pas d'interface intuitive d'où l'intéret de cette section.

Automate des états du programme

Contrôles

[Entrée]	Sélection affichage des faces/arrètes.
[N]	Activation/Désactivation du gouraud shading.
[L]	Activation/Désactivation de la lumière.
[Gauche]/[Droite]	Zoom
Souris	Rotation de l'objet
[Page Up]/[Page Down]	Taille des deux sphères de sélection de points
[E]	Sélection du point PA, le plus proche du curseur de la souris.
[D]	Sélection du point PB, le plus proche du curseur de la souris.
[P]	Déplacement du point PA à l'opposé de PB.
[M]	Déplacement du point PB à l'opposé de PA.
Etat1
[ESPACE]	Lancement du calcul du chemin entre PA et PB.
[G]	Passage en mode Création du chemin à la main à partir du point PB.
Etat3
[<>]	Sélection du point suivant.
[Shift]	Validation du point sélectionné.
[ESPACE]	Passage à l'état 4.
Etat4
[Haut]/[Bas]	Réglage du nombre d'itérations de l'algorithme d'optimisation du chemin.
[I]	Afficher/Masquer le chemin initial.

Notes

Le chemin du fichier OFF est à rentrer dans le fichier Parametres.h
Il n'est pas possible de tracer plusieurs chemins dans une session du programme...
Le critère utlisé dans le programme pour la construction du chemin est: choisir le voisin P_i+1 tel que T(P_i+1) est minimum.

Bilan

Conclusions sur l'algorithme étudié

Le chemin initial semble assez approximatif par rapport aux algorithmes du sujet n°1. La FMM nous a paru trop générale pour traiter de façon optimale le problème spécifique d'une source ponctuelle. De plus, la convergence du chemin corrigé est trop lente pour corriger ces manquements. En effet, si le lissage du chemin est très rapide, le redressage à moyenne échelle est quand à lui très long.
Mais, même si nous n'avons pas eu le temps de mener une étude comparative, il semblerait que la FMM soit plus rapide. Cependant, il semble difficile de l'améliorer pour calculer des straightest geodesics. De plus le problème du choix d'un coté plutôt qu'un autre dans l'algorithme d'optimisation rend les straightest geodesics encore plus difficille à implémenter.

Ce que ce projet nous a apporté

Ce projet nous a permis de nous initié à OpenGL, ce qui était un de nos objectifs. En renonçant à utiliser CGAL, nous avons aussi eu la possibilité de créer et manipuler des structures de représentation de surfaces 3D assez complexes. Mais la partie la plus enrichissante fut certainement l'étude de publications de recherche assez récentes. Il n'a pas toujours été possible de répondre à nos questions par une recherche sur internet, ce qui nous a obligé à prendre des initiatives puis à les valider. Ce fut pour nous une première expérience du monde de la recherche qui nous a définivement donné envie d'en faire partie !
Ce projet a donc été très formateur parce qu'il nous a initié à la programmation 3D mais surtout parce qu'il nous a fait toucher aux différentes étapes de la recherche (documentation, développement/innovations et rédaction d'un rapport).
Nous avons eu beaucoup de plaisir à le faire.

Ce qu'il reste à faire

L'implémentation par tas ne fonctionne pas
Explorer l'idée de ne plus considérer certains points du chemin afin d'acélérer la convergence de l'algorithme

Nous regrettons également de ne pas avoir eu plus de temps pour faire un programme un peu plus convivial. Notre programme est en effet plus un laboratoire d'expérimentations pour tester les algorithmes qu'un délivrable utilisable par quelqun d'autre que nous...

Projet Image Calcul itératif de géodésiques discrètes Antoine MELER & Adrien BERNHARDT

Sommaire

Introduction