Variational Shape Approximation
Résultats
Variational Shape Approximation
Nous avons implémenté une classe VarShapeApprox qui donne un ensemble de méthodes pour appliquer notre algorithme. On trouve également la classe Proxy, qui rassemble tous les attributs et traitements propres à une région.
Initialisation

Il existe deux manières d'initialiser l'algorithme de création des régions:
- on choisit n triangles au hasard sur l'objet: ils constituent le point de départ des n régions. Ensuite il suffit d'appliquer la première étape de l'algorithme qui consiste à faire croître chaque région jusqu'à obtenir une partition du modèle (image de gauche).
- au départ, le modèle n'a qu'une région. Puis on ajoute les régions une à une jusqu'à obtenir le nombre de régions désiré par l'utilisateur. Cette initialisation s'adapte bien aux objets de forme géométrique (pièces mécaniques par exemple, comme sur l'image de droite). Cette méthode est néanmoins plus coûteuse en temps de calcul.
Algorithme d'approximation

Le but de l'algorithme est de créer des régions connexes, composées d'un ensemble de triangles du modèle. A chacune de ces régions est associé un plan qui approxime au mieux l'ensemble des triangles de la région, au sens d'une mesure (L2 ou L21 dans notre cas).
Nous avons découpé le coeur de l'algorithme en trois méthodes appelées respectivement initialSeeding, distMiniFlooding et proxyFitting: elles correspondent exactement aux étapes de l'algorithme décrit dans l'article Variational Shape Approximation de Cohen Steiner:
- pour chaque région on choisit le triangle le plus proche du plan: il sert de point de départ pour réappliquer la première étape de l'algorithme.
- une fois l'initialisation faite, il suffit d'associer à chaque région les triangles qui sont les plus proches du plan correspondant (toujours au sens d'une mesure donnée).
- enfin, les plans sont ensuite recalculés de manière à minimiser l'erreur d'approximation entre les triangles de la région et le plan.
Automatisation de l'algorithme
L'utilisateur peut modifier interactivement le nombre de régions du modèle. Pour cela, il dispose de 3 boutons: un pour l'ajout, un pour la suppression et un pour la téléportation de région. Mais il est également possible de rendre automatique l'algorithme: il s'applique tant qu'un seuil d'erreur totale sur le maillage n'est pas atteint. Il ajoute à chaque boucle une région, et téléporte de temps à autre.
Détection et découpage des régions non topologiquement équivalentes à un disque

Nous avons été confronté à un problème lors du codage de la phase de remaillage: en effet, bien que les régions soient connexes, il se peut qu'elles ne soient pas homéomorphes à un disque et possèdent donc plus d'une frontière. Les polygones créés à partir des points placés sur les frontières n'ont donc plus aucune raison d'être bien formés. Dans un premier temps, nous avons tenté de parcourir les frontières dans un certain ordre et de placer des segments pour passer d'une frontière à une autre de manière à créer un polygone correctement formé, mais cet algorithme très complexe n'a pas abouti car d'autres problèmes ont fait leur apparition, notamment lorsqu'il n'y a pas suffisamment de points sur une frontière (cf illustration ci-dessous).
Finalement, plutôt que de créer des polygones s'adaptant aux régions, nous avons décidé de modifier les régions elles-même. Ainsi, toutes les régions possédant plus d'une frontière sont divisées récursivement jusqu'à ce qu'elles soient toutes homéomorphes à un disque (cf image)
Remaillage
Extraction des ancres
Les premières ancres, qui sont en fait les sommets du modèle remaillé, sont placées aux intersections d'au moins trois régions. Cependant, il faut au minimum trois points par région pour créer un polygone, ce qui n'est absolument pas garanti à cette étape. Nous avons donc implémenté une fonction permettant d'ajouter ces points manquants en les répartissant équitablement sur la frontière.
Triangulation - Polygonisation

Cette étape consiste à trianguler les polygones obtenus précédemment. L'algorithme utilisé est un Dijkstra multisource, les ancres du polygone étant les sources (on leur attribut une couleur unique) et les longueurs des arêtes sont les poids. Ainsi, les sommets d'une région du modèle original sont colorés avec la couleur de l'ancre la plus proche jusqu'à obtenir une partition de celle-ci. Il ne reste qu'à rechercher les triangles dont les trois points ont des couleurs différentes. Ces trois couleurs indiquent quelles sont les ancres qui doivent être regroupées pour former un nouveau triangle.
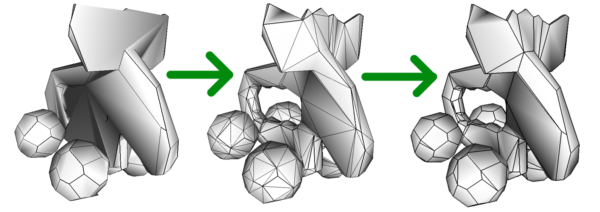
La dernière étape consiste à regrouper les triangles pour former des polygones. Il s'agit de choisir quels sont les triangles à regrouper de manière à former les meilleurs quadrilatères (au sens d'une mesure de qualité développée dans P. Pebay 2002). On procède ensuite à un dernier regroupement pour former des polygones: pour qu'il soit validé, le polygone doit rester convexe et la normale issue du regroupement ne doit pas dévier de plus de 20 degrés par rapport à celle d'origine.
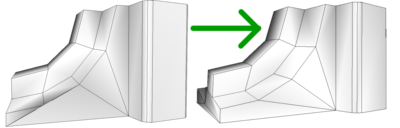
Nous avons amélioré le maillage final en inversant certains triangles adjacents. Sur l'image ci-contre vous pouvez observer l'action de la transformation. Certains triangles ont été modifiés et le maillage est a priori de meilleure qualité.
Analyse critique
Performances
Temps de fonctionnement
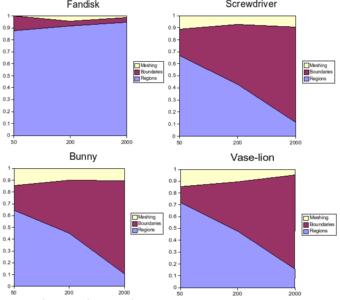
Nous avons effectué quelques tests sur des modèles de complexité variée. Dans tous ces tests, le nombre de régions est fixe et aucune téléportation n'a été effectuée. Pour la pièce mécanique (fandisk) nous avons utilisé l'initialisation prévue pour ce genre de modèles, ce qui augmente le temps de calcul mais donne de meilleurs résultats.
Les graphes donnent les temps que prennent chacune des étapes de l'algorithme en pourcentage du temps total: le calcul des régions ("Regions"), le calcul des frontières ("Boundaries") et le remaillage ("Meshing"). Les tests sont effectués avec 50, 200 et 2000 régions, et ceci pour quatre modèles:
- Fandisk.off : 13.000 faces
- Screwdriver.off : 54.000 faces
- Bunny.off : 70.000 faces
- Vase-lion.off : 400.000 faces
On remarque que dans le cas du fandisk, la plupart du temps est consacrée au calcul des régions: en effet, l'initialisation pour les objets géométriques est plus lourde puisqu'il y a autant d'itérations sur l'algorithme principal qu'il y a de régions.
Sur les trois autres graphes, on constate que lorsqu'on augmente le nombre de régions, le calcul des frontières devient un point critique de notre algorithme: il faut pour chaque région, parcourir les frontières, ce qui peut devenir lourd si le modèle possède énormément de faces et de régions. Le problème est également dû à notre implémentation qui pourrait être optimisée.
Enfin, les temps de calcul varient de 8 secondes pour fandisk avec 50 régions, à 5min30s pour vase-lion avec 5000 régions (tests effectu?s sur un pentium D 2.8GHz), ce qui reste raisonnable pour des objets d'une telle complexité.
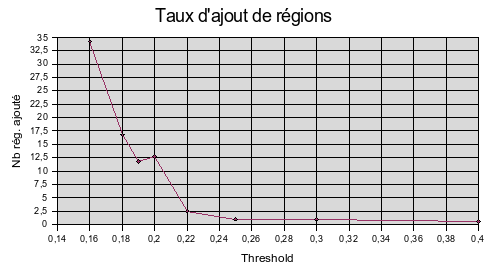
Taux d'ajout de régions
L'algorithme d'approximation automatique ajoute une région à chaque boucle et en téléporte une toutes les 5 boucles, jusqu'à ce que le seuil d'erreur totale exigé est atteint. Le graphe représente le nombre de régions ajouté à un nombre initial de 30 régions, sur le modèle suivant: horse-cyberware.off: 97.000 faces.
On remarque que tout d'un coup on vient ajouter beaucoup de régions. En connaître l'allure globale est impossible, ceci pour une raison non encore corrigée: l'algorithme sature et s'arrête.
Problèmes non résolus...
...avec la distance L2
Notre algorithme fonctionne avec deux mesures de distances différentes : L2 et L21. Or la distance L21 a donné des résultats satisfaisants dès le début, en revanche la distance L2 donne des colorations qui peuvent être très étranges. En effet, des strates apparaissent qui donnent du fil à retordre à l'algorithme de remaillage.
Au départ les résultats étaient véritablement abhérents, mais après la correction de l'erreur de la formule de calcul de la matrice de covariance présente dans une ancienne version de l'article de recherche de Cohen Steiner, le problème n'a plus l'air de se poser avec un nombre conséquent de régions.
...lors du remaillage

Certaines erreurs surviennent lors de l'exécution de notre algorithme, et plus particulièrement à l'étape de remaillage : ces erreurs sont directement liées à la géométrie particulière de certains modèles. Certaines ont été identifiées mais toutes n'ont pas été corrigées, faute de temps :
- à l'issue de l'étape de création des régions, les premiers sommets du nouveau modèle sont ajoutés à l'intersection de 3 régions. Même si toutes les régions sont homéomorphes à un disque, il se peut que le polygone constitué par les nouveaux sommets d'une région ne soit pas convexe, ce qui pose des problèmes de recoupement de surfaces.
- OpenMesh n'autorise pas les modèles qui ne sont pas 2-manifold. Ceci pose problème lorsque notre algorithme de remaillage tente d'associer plus de 2 faces à une même arête (cf illustration). L'un des deux cas que nous avons identifié a été traité.
- d'autres erreurs non expliquées (manque de temps pour les identifier) se produisent et sont sûrement une conséquence des précédentes.
Déroulement du projet
Compréhension du document
Tout notre projet s'est basé sur le document Variational Shape Approximation de D. Cohen-Steiner, P. Alliez et M. Desbrun. La difficulté n'a pas été la langue anglaise mais plutôt de comprendre ce qui manque dans les explications pour en déduire un algorithme fonctionnel.
Nous avons aussi été confronté à une erreur dans la version du document que nous avions au niveau de la formule de la matrice de covariance. Nous avons alors contacté P. Alliez qui nous a très rapidement répondu et nous a alors dirigé vers une version plus récente du document ainsi que son code source pour le calcul de la matrice de covariance. Par ailleurs nous avons mal compris le critère de subdivision, ce qui nous a amené à passer plusieurs jours sans réussir à le faire marcher.
Développement de VarShapeApprox
Pour cette partie le document est très clair, nous avons pu directement implémenter l'algorithme, tout du moins pour la distance L21. En effet le calcul des valeurs propres d'une matrice n'est pas chose facile et nous a donné du retard sur une distance L2 fonctionnelle.
Nous travaillions alors avec un nombre préfixé de régions. Pour l'ajout et la suppression nous devions passer à un nombre dynamique de régions, ce qui nous a amené à utiliser une deque<Proxy*> et modifié le code en conséquence.
Nous y sommes revenus à la fin de notre projet pour ajouter les fonctions permettant de supprimer les régions à multiples frontières, ainsi que pour regrouper des parties du code en une et une seule fonction d'accumulation et corriger la fonction de fusion de deux régions.
Développement de Meshing
Le remaillage a eu un développement simultané sur plusieurs étapes:
- Les premiéres étapes qui créent une esquisse du maillage ont été rapidement implémentées.
- L'étape de la coloration suivant les ancres s'est vu être reprise une fois car l'algorithme implémenté au départ était erroné.
- L'étape de triangulation a fonctionné tout de suite, en revanche l'utilisation de la fonction garbage_collection a posé quelques problèmes ainsi que les cas particuliers cités précédemment dont un a été réglé : le cas des triangles "double-face".
- La polygonisation s'est bien passée, en revanche un autre article a été consulté, Some Results about the Quality of Planar Mesh Elements de P.P. Pebay, pour trouver un bon critère de création des polygones aprés la transformation en quadrilatères.
- Une rapide fonction pour faire en sorte que chaque région possède au moins 3 ancres.
- Rapidement nous avons remarqué des petites erreurs dans le maillage triangulé, que nous avons corrigées en inversant certains triangles adjacents. Le critère de décision a aussi été difficile à rendre fonctionnel.
- Un essai de correction des frontières multiples. La complexité nous a poussé à abandonner l'idée.
Apports du projet
Par ce projet, nous avons été amené à comprendre une publication de la recherche, ce que nous n'avons pratiquement jamais fait auparavant dans nos études. Nous avons aussi dû concevoir une structure entière du programme pour nous permettre d'arriver à nos fins. Les heures de débogage ne nous empêcherons jamais de ne pas avoir à déboguer à l'avenir mais nous ont permis de véritablement acquérir une certaine méthodologie. Nous avons été amené à améliorer une interface autant pour faciliter le débogage, que mettre en valeur notre travail. Beaucoup de projets logiciel demandent cette étape dans leur développement.
Le contenu est aussi quelque chose qui nous intéresse. Nous avons déjà touché à des logiciels de conception de maillages, été subjugué par des effets spéciaux dans des films et ce projet nous a permis d'entrevoir l'envers du décor, le code source de ce genre de logiciel et la manière dont ils peuvent fonctionner.