Julien Barrois, Sami Bendouba, Mélissa Faucher & Rémi Fayolle
Tuteur : Franck Hetroy



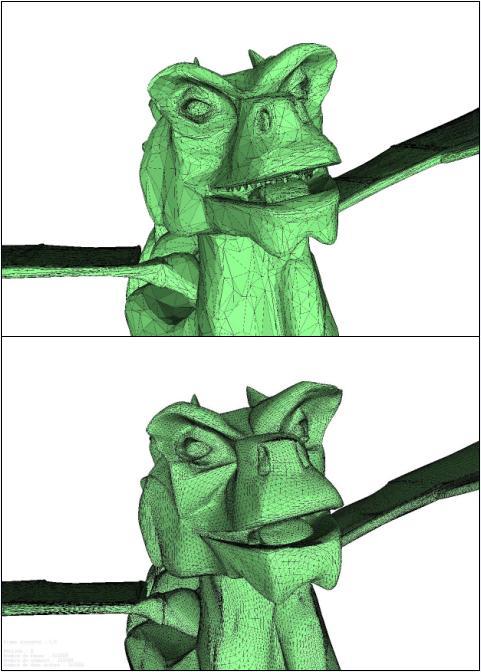
dragon de base, dragon simplifié (95% des sommets avec Garland-Heckbert) et dragon remaillé (3 itérations)
Sommaire
Introduction

Le but de ce projet était d'implémenter un remaillage semi-régulier de séquences en vue de les compresser. On s'est basé sur l'article Semi-Regular Representation and Progressive Compression of 3-D Dynamic Mesh Sequences, par J.-H. Yang, C.-S. Kim et S.-U. Lee (IEEE Trans. Image Processing 2006). La méthode se déroule selon le schéma suivant :
- simplification des maillages
- remaillage du premier maillage de la séquence
- estimation du mouvement entre les maillages
- remaillage de chaque maillage à partir des étapes précédentes
On voit tout de suite l'intérêt que représente un tel projet. En effet, l'animation 3D est aujoud'hui au coeur de la communication et des applications industrielles. Tout au long du projet, on a pu voir que les limites matérielles (de machines pourtant très puissantes avec 2 processeurs cadencés chacun à 2.8GHz, 1Go de RAM et 2Go de cache) étaient vite atteintes par notre application. La nécessité de compression de ces animations est donc évidente.
1. Technologie et interface
Le développement de l'interface a fait appel à diverses technologies logicielles. En effet, nous sommes partis d'une interface basique affichant de simples maillages pour finalement arriver à quelque chose d'assez complet, permettant de visualiser des séquences d'animation dans un format VRML simplifié, ainsi que de les remailler de façon semi-régulière. Détaillons les différentes composantes du logiciel.
1.1 L'interface, une QApplication

L'implémentation de l'interface proprement dite s'est faite en utilisant la librairie Qt. En effet, lorsque l'on maitrise un peu la technologie, cela permet de gérer assez bien une application grâce au mécanisme de signaux et de slots. La gestion des menus avec les modifications des propriétés d'affichage et des réglages est donc gérée grâce à Qt. L'interface communique donc avec le viewer, expliqué ci-dessous.

1.2 Le viewer, une extension d'un QGLViewer

L'interface de visualisation utilisée est une extension d'un viewer qui a été développé dans les locaux de l'IMAG : QGL Viewer. Il permet d'afficher des scènes 3D ou des séquences d'animation grâce à la librairie fournie avec : libQGLViewer. Il utilise le moteur de rendu OpenGL pour afficher les objets à l'écran.
Nous avons modifié le viewer basique pour pouvoir charger des animations (fichier VRML parsés). On a aussi rajouté plein d'options (plus ou moins utiles) : choix des couleurs (fond, faces, arêtes), affichage d'infos à l'écran sur la séquence, fonctions pour l'animation (frame suivante, frame précédente, lecture, pause, marche avant/arrière) ...
La principale modification vient de l'ajout d'un menu "Modeling" qui nous permet d'utiliser les algorithmes implémentés lors de ce projet, notamment la simplification et le remaillage des modèles. En effet, le viewer charge en mémoire le ou les maillages (selon si c'est une animation ou non). On peut alors les modifier à souhaits grâce à des procedures extérieures, et il permet de visualiser les résultats.
Le viewer affiche les objets grâce à une méthode draw() qui parcourt l'objet contenant le maillage et qui affiche les données souhaitées (faces, sommets, arêtes, ...). Cette méthode utilise la librairie OpenGL qui permet d'afficher ce qu'on veut. Lorsqu'il s'agit d'une animation, la méthode draw() alterne avec la méthode animate() qui s'occupe de l'animation. En fait, il suffit de modifier le numéro de la frame courante pour que la bonne frame s'affiche.
1.3 OpenGL, la librairie d'affichage

Dans le viewer, on utilise la librairie OpenGL pour afficher les faces, les sommets, les arêtes, ou même pour gérer la lumière et le lissage d'un maillage (grâce aux normales). Nous avons donc principalement utilisé l'affichage des faces grâce au parcours des sommets, l'affichages des arêtes, ainsi que la gestion de la lumière grâce aux normales.
Structures de données
Le sujet nous proposait de travailler avec OpenMesh, une librairie de manipulation de maillages 3D. Cependant, après plusieurs échecs pour compiler des programmes simples avec cette librairies, nous avons décider de construire nous même nos classes pour manipuler des Mesh, PimpMyMesh.
Cette structure de données se rapproche de celle proposée pas OpenMesh :
- Chaque demie-arête a référence à son sommet de départ, son sommet d'arrivée, la face triangulaire qui lui correspond, l'arête suivante dans cettes face et une référence vers son arête opposée dans le mailage.
- Chaque Sommet possède les références des aretes dont il est le départ
- Chaque face pointe vers une des arêtes qui la bordent.
Un maillage est une collection de face, de sommets et d'arêtes.
Simplification d'un maillage
La simplification du maillage a été implémentée suivant l'algorithme de Garland et Heckbert. Cette algorithme qui consiste à contracter des sommets entre eux peut être résumé ainsi :
- On sélectionne les couples de sommets qui pourront être contractés. Chacun de ces couple constitue une paire valide pour chacun des quel on calcule le sommet résultant de la contraction, et un coùt. Dans notre algorithme, nous considérons que les paires valides sont celles où il y a une arête dans les deux sens entre les deux sommets.
- On effectue les contractions une à une en effectuant toujours celle de coût minimum.
- Après chaque contraction, on mais à jour les paires contenant un des deux sommets de la contraction.
Pour trier les paires en fonction de leur coût, on utilise un arbre binaire de recherche, ainsi le recherche du minimum et la suppression et l'insertion sont en temps logarithmique. Cette implémentation permet d'atteindre des performances proche de ce que l'on peut trouver dans le commerce.
Il existe certains cas où nous n'effectuons pas la contraction car la configuration n'est pas propice à une contraction simple. Dans ce cas, nous multiplions le coût de la contraction par 100 avant de réinsérer la paire dans l'arbre.
Voilà quelques exemples de ce que l'on obtient :
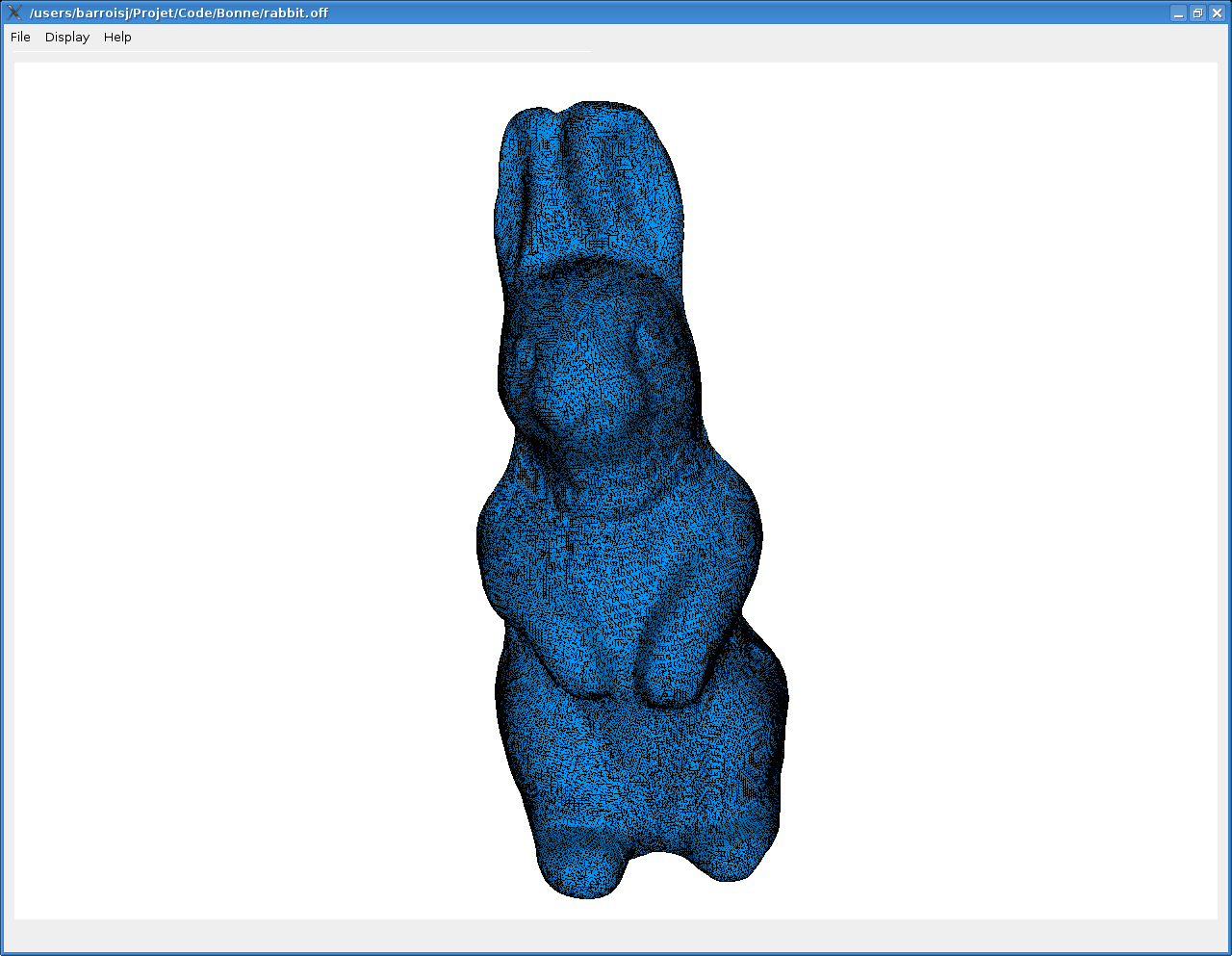
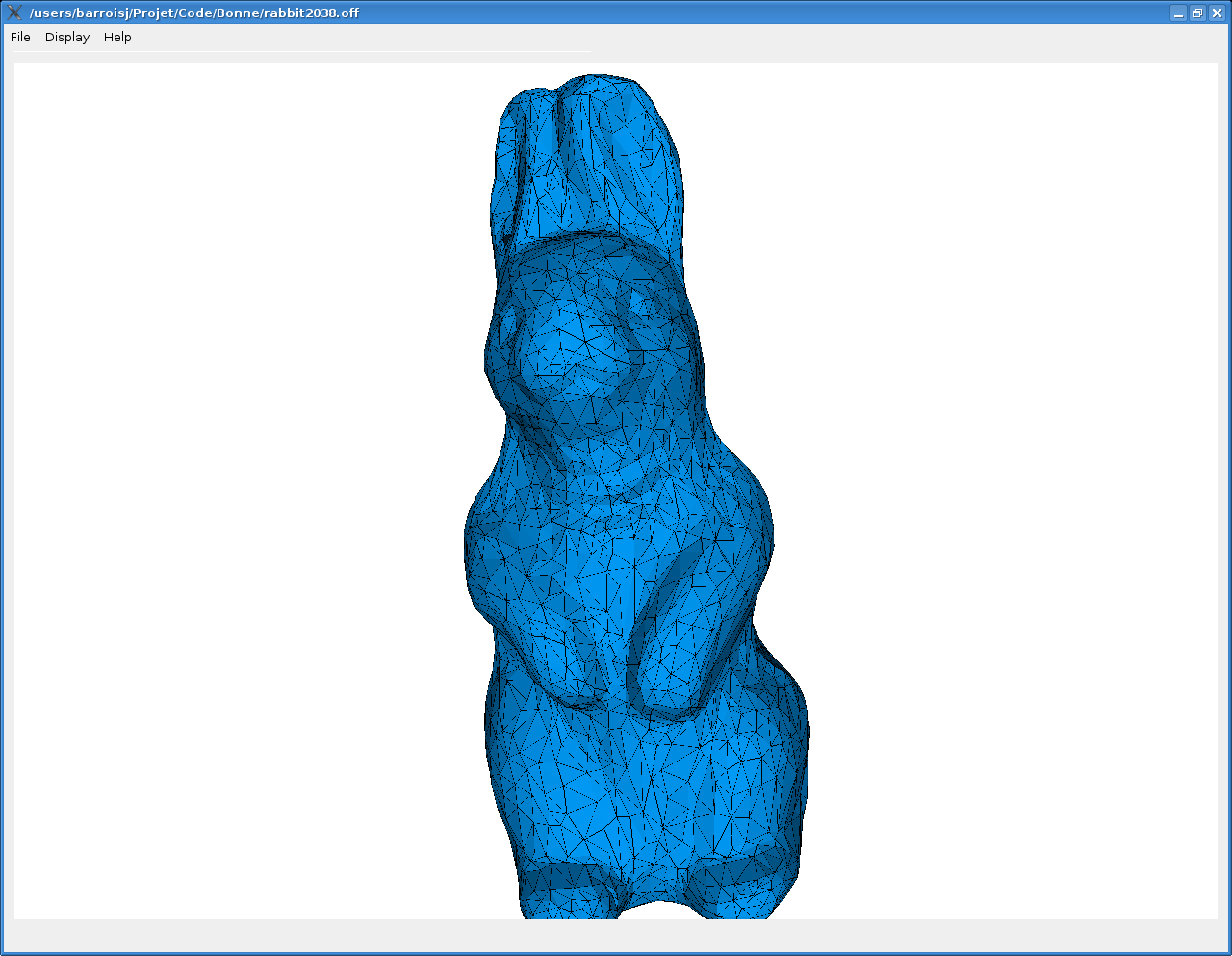
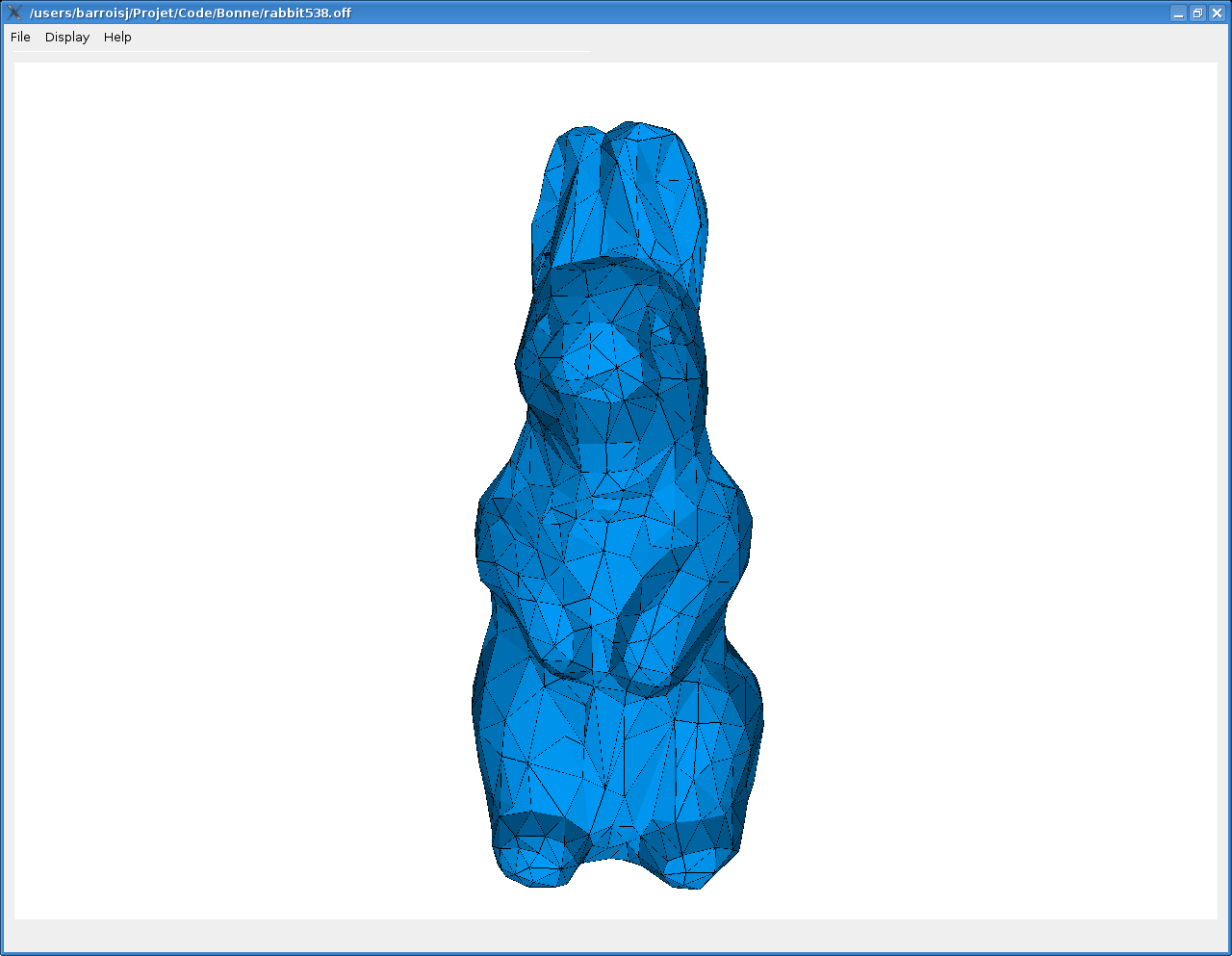


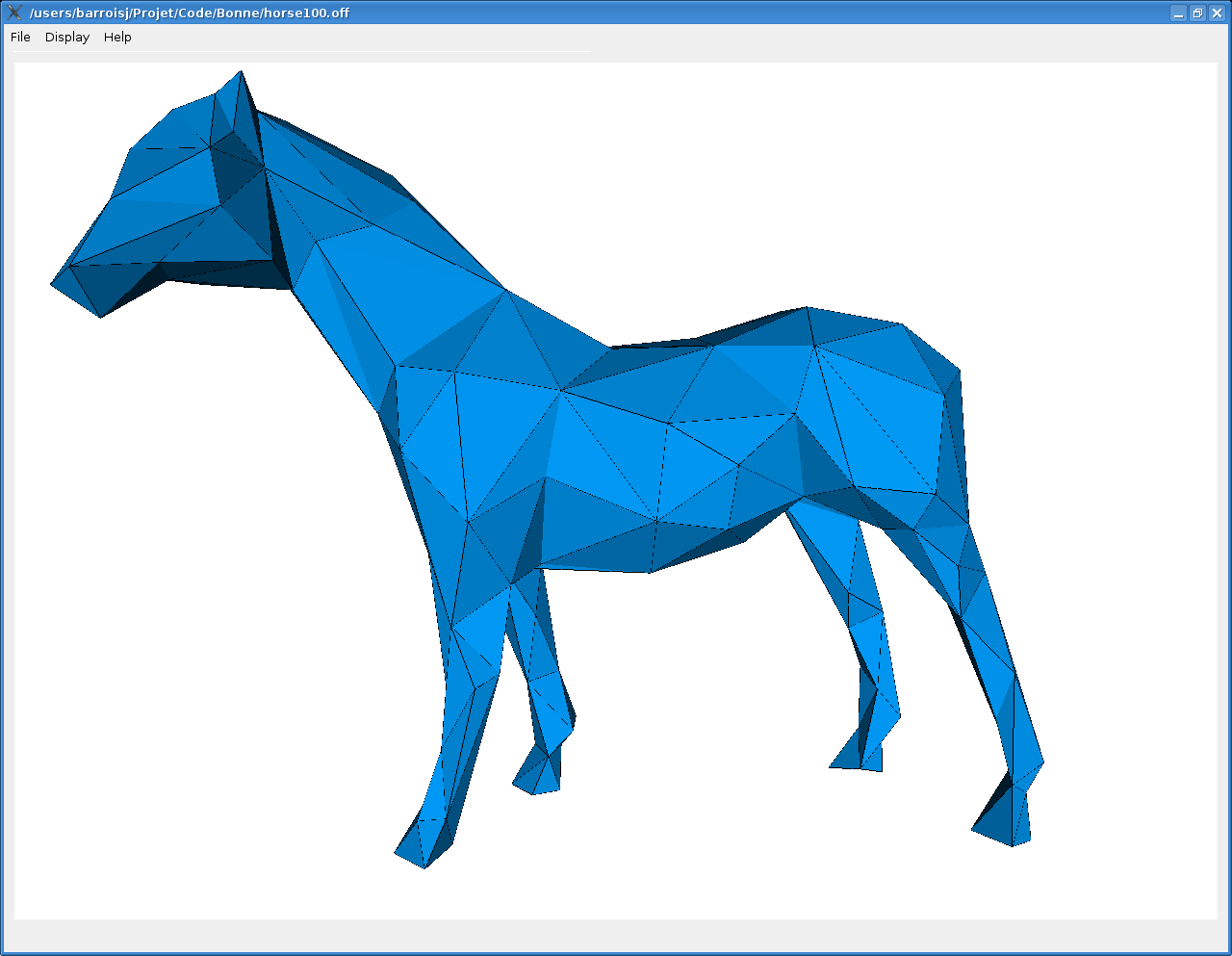
On peut remarquer plusieurs choses :
La qualité globale de la simplification est putôt bonne, on arrive à préserver la forme général de l'objet.
On traite de la même manière tout les points du maillage, alors qu'il serait judicieuxde porter l'accent sur certains sommets qui somt plus importants dans la forme gloable de l'objet.
C'est ce que l'on a essayé de faire en ajoutant un critère de sallience à nos sommets. Ce critère prend on compte la sallience à plusieurs échelles comme il est expliqué dans l'article "Mesh saliency". Il s'agit de mettre en valeur les sommets étant le plus sur des "coins" et des "pics" par rapport à d'autre qui sont situés sur plan par rapport à leur voisin. Cette mise en valeur se traduit par une augmentation du coût des contractions correspondantes à ces sommets. De cette manière, nous arrivons à préserver plus d'informations importantes quant à la forme générale de l'objet :
On voit pas exemple sur l'image suivante qu'avec un critère de sallience, le détail des doigts d'homer sont beaucoup mieux préservés avec un ritère de sallience.
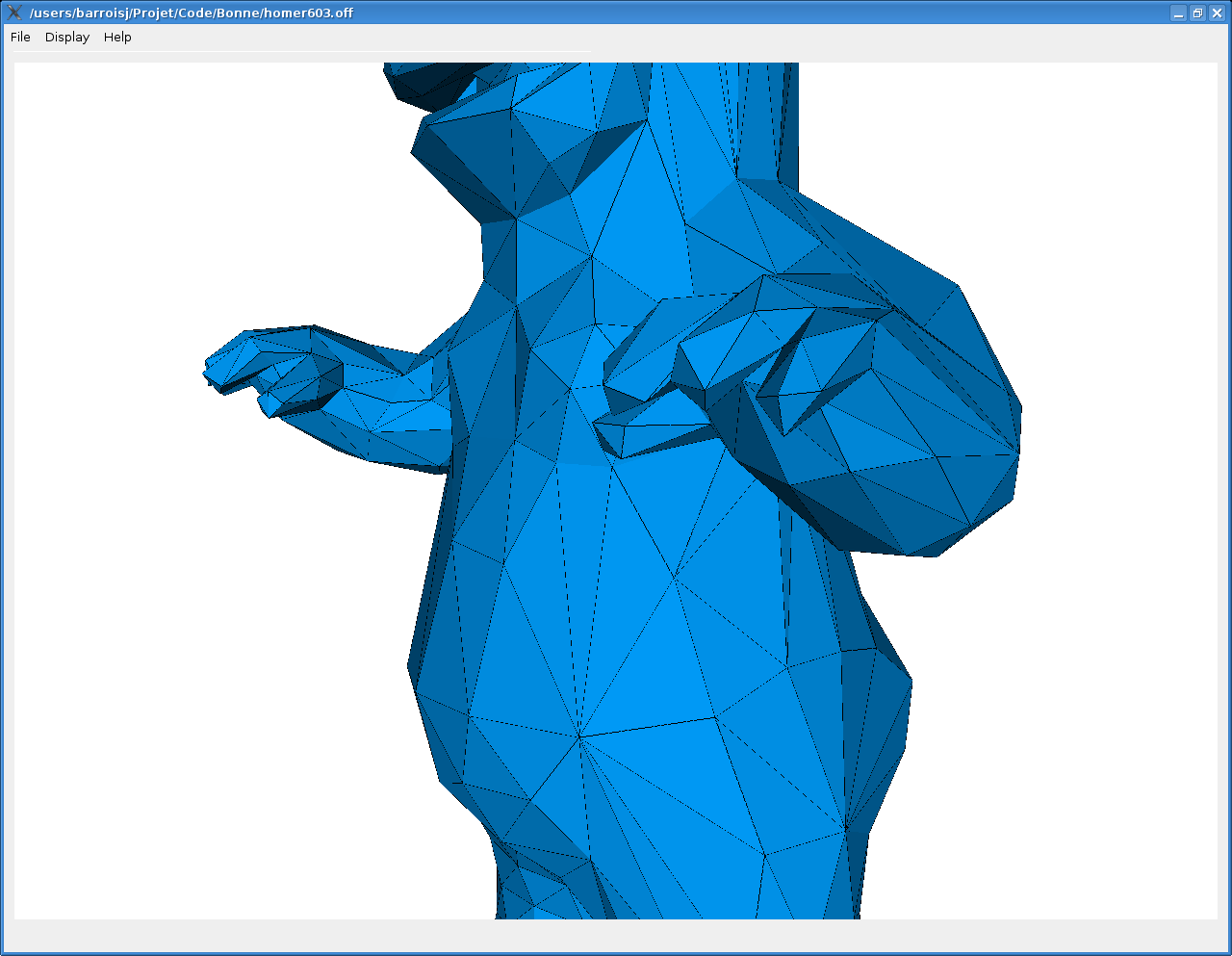
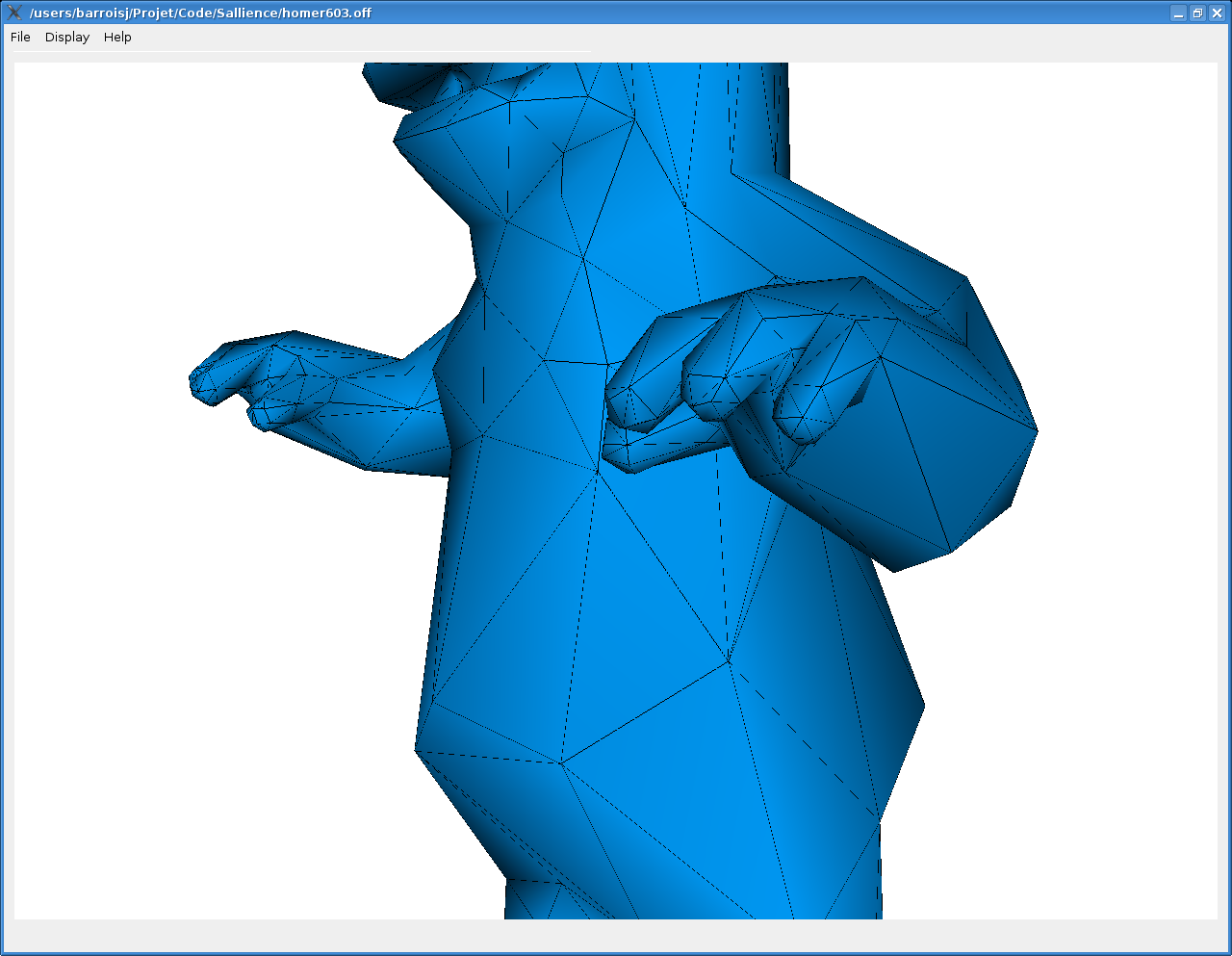
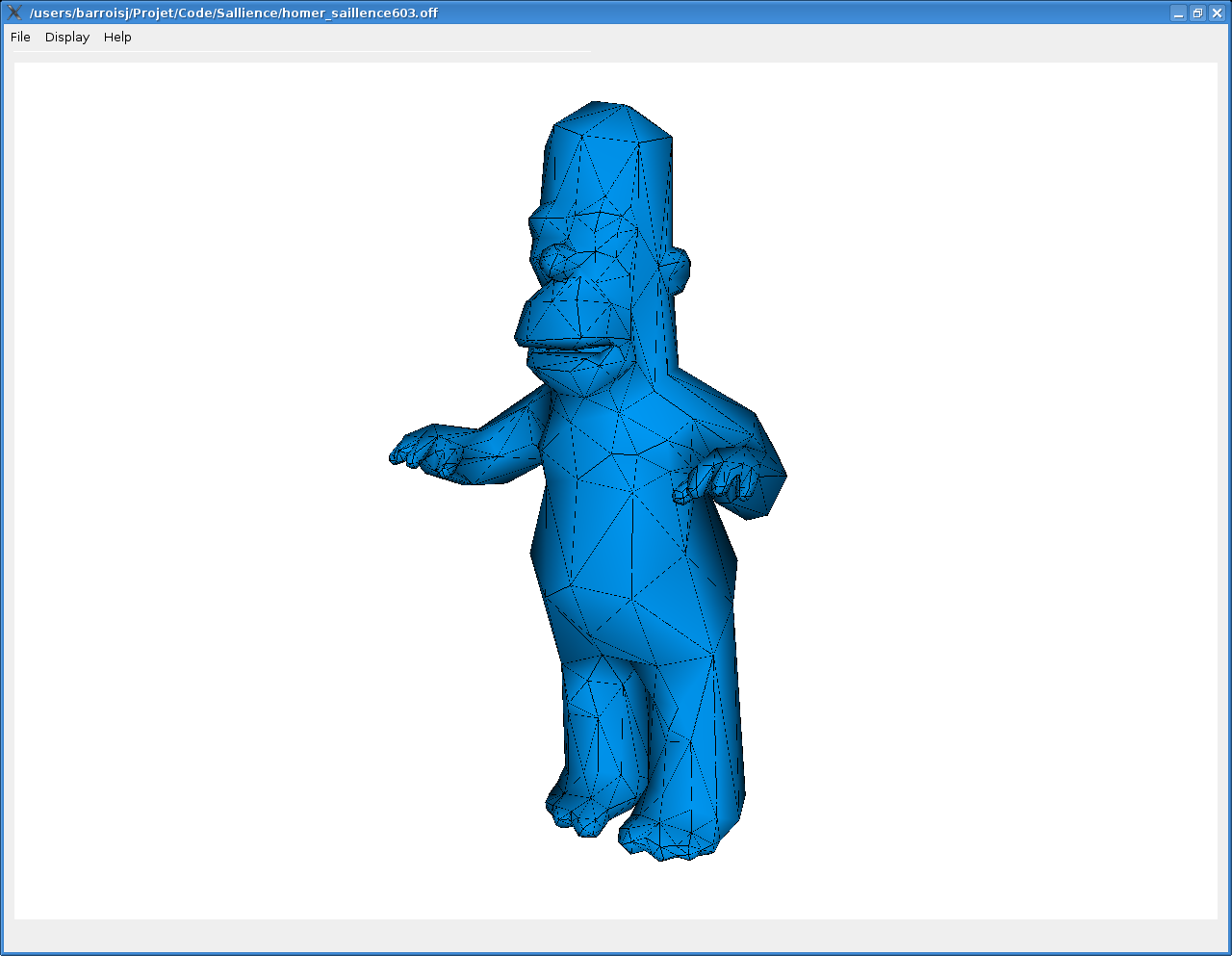
Cependant, cette technique dépend de plusieurs paramètres dont il est difficile d'intuiter les valeurs optimales pour un maillage donné.
- La taille des échelle qui correspond à un certain pourcentage de la diagonale de la boite englobant le maillage ( 0.003 dans l'exemple précédent)
- le seuil à partir duquel on favorise un sommet du maillage ( nous avons choisi 0.. fois la valeur maximale )
- le facteur par lequels on multiplie le critère de sallience des sommets étant au dessus du seuil ( que l'on a fixé arbitrairement à 50)
Le bon choix de ces paramètres permet de trouver l'équilibre entre le fait de favoriser les sommets important sans trop négliger les autres parties du maillages.
Cette technique à un autre inconvénient(qui dépend certainement de la façon dont nous l'avons implémenté), c'est le temps de calcul des critères de sallience de chaque sommet. En effet, pour chaque sommet, on doit parcourir tous les sommets voisins (directement ou indirectement) situés à une certaines distance, et ce pour tous les sommets du maillage. Ce temps pourrait peut-être améliorer avec du multi-threading, mais certaines autres contraintes apparaitraient alors ( exclusion mutuelle lors du marquage des sommets déjà visité, ...).
4. Remaillage
4.1 Projection des sommets supprimés sur les faces du maillage simplifié
L'article de référence principale (Semi-Regular Representation and Progressive Compression of 3-D Dynamic Mesh Sequences, par J.-H. Yang, C.-S. Kim et S.-U. Lee) propose d'accompagner lors de la simplification du maillage l'algorithme de Garland et Heckbert par une projection des sommets supprimés sur une face nouvellement créée. Pour cela, on construit un plan minimisant la distorsion métrique entre du voisinage du point à modifier : la conformal map.
On travaille ensuite dans cette conformal map : on affecte un SommetTemoin (barycentre de 3 points) au projeté du sommet supprimé. On met également à jour les SommetTemoin préalablement calculés, appartenant à une face affectée par la suppression du sommet.
A la fin de la simplification, certaines faces du maillages possèdent ainsi une liste de SommetTemoin, identifiés par leurs coefficients barycentriques par rapport à ses sommets. Ces SommetTemoin constituent des informations utiles au remaillage du mesh.
4.2 Butterfly
La technique Butterfly permet de subdiviser chacune des faces (triangulaires) en 4 nouvelles faces.
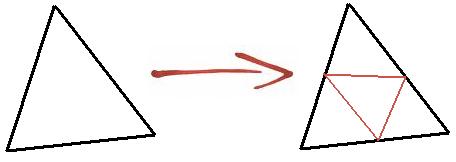
Principe de subdivision d'une face du mesh
Il consiste à choisir un sommet sur chacune des arêtes de la face prenant en compte les positions des 8 sommets environnants : pour ce faire, on calcule le barycentre des voisins de l'arête dotés des coefficients ci-dessous :
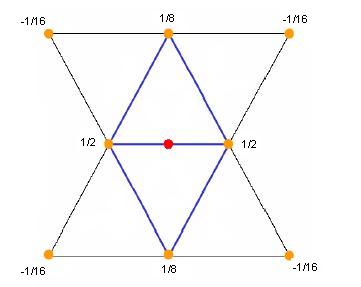
Subdivision Butterfly
En jaune : les 8 sommets utilisés pour le calcul du Butterfly
En rouge : le sommet Butterfly, barycentre des voisins affectés de leurs coefficients
Ces sommets Butterfly sont construits et rajoutés au mesh, ainsi les demi-arêtes et les faces créées, dans la fonction Mesh::Remaillage.
4.3 Remaillage du mesh
Pour le remaillage, l'article de Yang-Kim-Lee préconise le calcul sur chaque arête du sommet Butterfly, et sa translation suivant la normale afin de trouver le sommet du maillage d'origine dont il est le plus proche : ce sommet devient le nouveau sommet utilisé pour la subdivision. Pour cela, il se sert des informations fournies par les SommetTemoins calculés au préalable et se trouvant sur les faces environnantes du Butterfly.
Nous n'avons pas réussi à temps à développer cette méthode, nous nous sommes donc contentés d'une simple subdivision Butterfly des faces, sans translation suivant la normale, qui donne cependant des résultats déja satisfaisants.
Les images ci-dessus montrent bien qu'une simplification Garland-Heckbert à 95% suivie d'un remaillage (constitué de 3 subdivisions Butterfly) n'affecte que peu la forme générale du maillage de départ : des détails tels que les narines, les arcades sourcilières ou les cornes, ainsi que le relief du visage, sont conservés, et le maillage résultant est très similaire à celui de départ. On peut cependant déplorer la disparition des dents du dragon, information perdue durant la simplification Garland-Heckbert. Une simplification basée sur le critère de salience pourrait permettre de pallier ce problème.
L'affichage des arêtes des maillages source et résultat ne laissent aucun doute sur l'efficacité de la semi-régularisation effectuée.
5. Estimation du mouvement
On a précédement réussi à simplifier, et à remailler un maillage. Pour remailler toute une séquence, on ne va pas appliquer ces algorithmes sur chacune des frames séparément, on va se contenter de remailler la première frame, et on va déduire grâce à l'algorithme ICP le mouvement entre les deux frames, et donc le maillage de la frame suivante.
5.1 L'algorithme ICP
L'algorithme ICP nous donne entre deux nuages de points la rotation et la translation optimale pour minimiser la distance moyenne entre les deux ensembles. Dans notre cas toutefois, on ne prendra pas la distance moyenne, mais on ponderera chaque distance en fonction des normales aux sommets, la manière de calculer ces poids n'étant pas détaillée dans l'article, on a pris la liberté de les rendre inversement proportionels à l'angle entre les deux normales (poids 1 pour un angle nul, 0 pour un angle de 180°).
5.2 Estimation du mouvement
On va ainsi partir de la première frame, simplifiée, pour chaque sommet de ce maillage, on lui associe le sommet du second maillage le plus proche de lui. On a ainsi deux ensembles de points comportant le même nombre d'éléments, on peut ainsi par plusieurs calculs ( notamment de cross-covariance) obtenir une matrice de rotation associée à un quaternion, et un vecteur translation.
Le problème étant que si cette méthode convient lorsque l'objet ne se déforme pas au cours du temps, elle pose problème dans le cas contraire. C'est pourquoi on va tout d'abord appliquer cet algorithme à tout le maillage de base, puis on va repérer les points s'écartant trop. On divise cet ensemble de points en ensembles connexes, et pour chacune de ces parties, on réapplique l'algorithme. On continue ainsi tant que la distance moyenne n'est pas descendue en dessous d'un seuil fixé. Typiquement sur un exemple comme le danseur, on va d'abord déplacer tout le danseur, puis comme les bras et les jambes s'écartent trop, on va traiter séparément ces quatres éléments. Une fois déplacés, les mains et les pieds seront mal placés, on va donc réappliquer de la même manière l'algorithme ICP sur ces parties.
5.3 Coût de l'algorithme
Soit n est le nombre de sommet de la première frame, et m celui de la seconde la recherche du voisin le plus proche se fait en n*m. Le calcul du vecteur translation et de la matrice de rotation se fait en n. Et enfin l'application des modifications en n. On a donc un algorithme qui calcule la simplification d'un mesh en O(n*m), la partie la plus lourde étant le calcul du point le plus proche.
5.4 Résultats
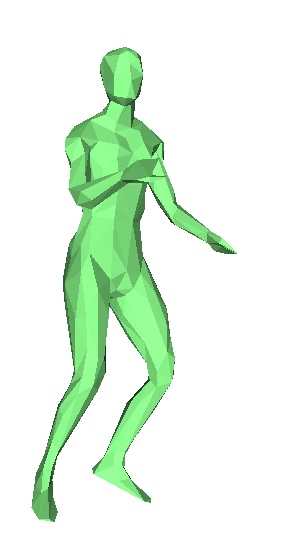
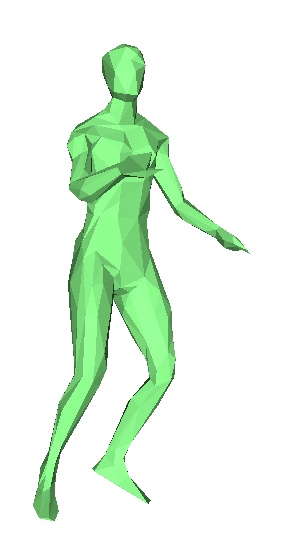
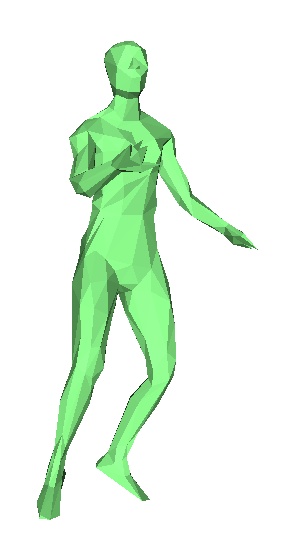
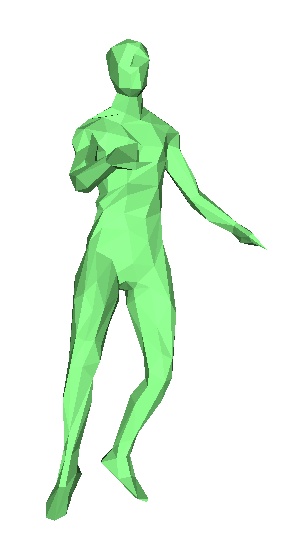
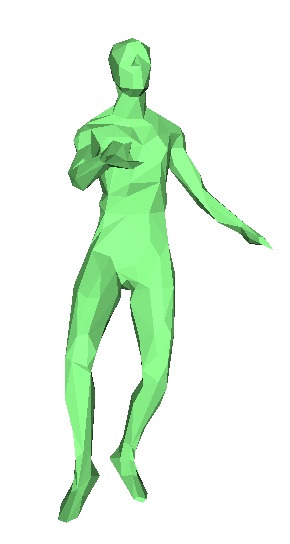
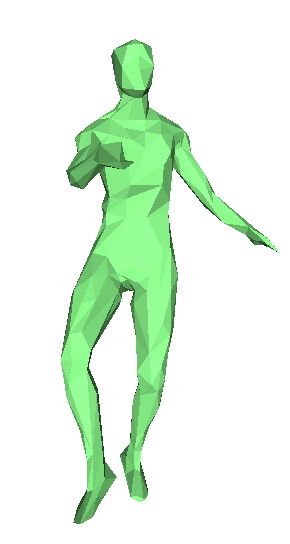
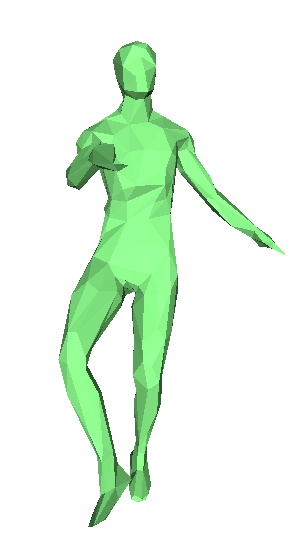
Le danseur originel, frames 1,2,3,4,5,6,7.
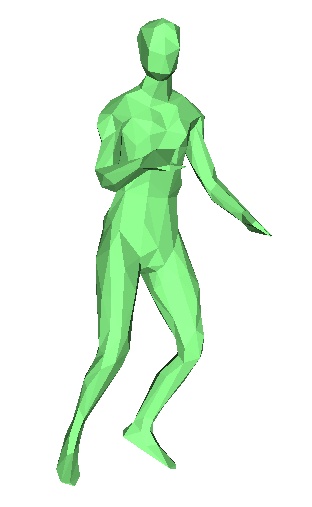
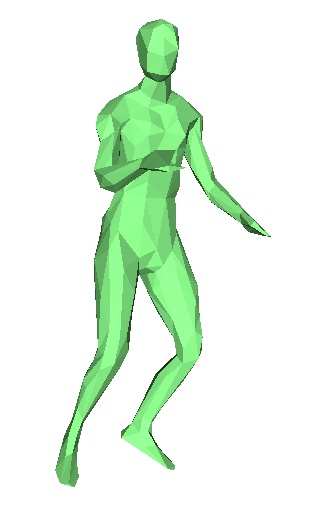
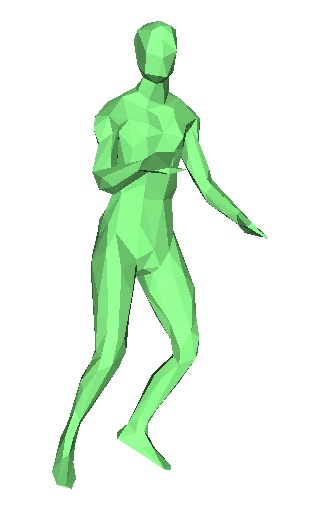

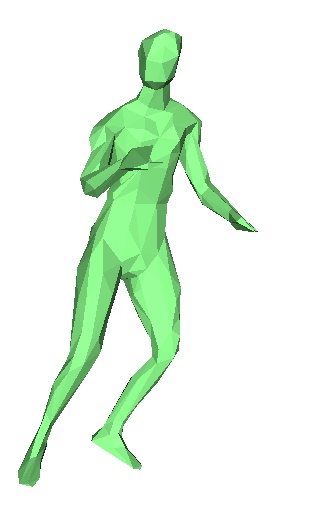


Le danseur après application de l'algorithme, frames 1,2,3,4,5,6,7.
En pratique, nous n'avons pas réussi à faire fonctionner correctement cet algorithme. En effet on observe rapidement au cours des frames des erreurs de plus en plus importantes. Chaque frame étant déduite de la précédente, la moindre erreur est rapidement accentuée. Toutefois on observe que le programme essaie bien de modifier les bonnes zones du maillages, pour le danseur par exemple, il va tenter de modifier pieds et jambes , mais les modifications ne sont pas correctes, et on se retrouve rapidement avec des énormes erreurs. Nous ne savons toujours pas à ce jour d'où vient l'erreur.
Conclusion
Pour conclure, nous pouvons affirmer que notre projet marche globalement, à l'exception de l'estimation du mouvement qui a encore quelques (gros) problèmes. Cependant, tout peut encore être amélioré. Par exemple, pour remailler l'objet, on pourrait subdiviser les faces en tenant compte des sommets de départ (utilisation de la conformal map et des SommetTemoin, abordée en 4.1).
Si nous trouvons le sujet très ambitieux, il en reste toutefois très intéressant. Nous avons apprécié la grande liberté de manoeuvre dont nous avons bénéficié durant ce projet. Nous sommes satisfaits d'être arrivés à un résultat final qui tient la route. Néanmoins, nous avons trouvé que les articles à rallonge et les algorithmes à tiroirs posaient problème : en effet, il était dur que chacun touche à tous les domaines de ce projet.