Introduction
Le but de notre projet est de reconstituer une animation à partir de maillages réels qui représentent le même objet articulé dans des positions différentes. Pour obtenir des maillages à partir d'objets réels, nous avons eu à notre disposition un scanner 3D.
Notre travail a donc consisté à apprendre à utiliser le scanner de façon à ce que les modèles soient utilisables par la suite, puis à réflechir à plusieurs méthodes d'approche du problème, pour enfin essayer d'implémenter la méthode choisie.
Utilisation du scanner
Pour notre projet, un scanner 3D nous a été prété par l'INRIA de Grenoble. Ce scanner permet de scanner des objets de taille petite à moyenne en trois dimensions. Il fonctionne à l'aide d'une interface qui est assez intuitive. Les paramètres à entrer pour effectuer le scan sont : le nombre de scan (nombre de rotation pour une position), la résolution du scan, la clareté de l'objet scannée, et la simplification du maillage souhaitée. Une fois les scans effectués, le logiciel essaie d'aligner les différents scans afin de reconstituer l'objet en 3D.
Problèmes rencontrés
Nous avons rencontré certains problèmes d'utilisation.
Après une première utilisation, et un premier résultat négatif sur un sujet présentant beaucoup de détails, et un second tout aussi négatif sur un objet de même taille, mais avec un niveau de détail peu élevé, nous nous sommes rendu compte qu'il fallait qu'on ajuste la distance entre la source laser et le sujet à scanner. Nous avons donc commencé par regarder à suelle distance devaient être scanner les objet.
Pour traiter le sujet proposé, il est utile d'avoir des modèles 3D relativement élaborés qui permettent de bien apprécier le mouvement. Nous avons donc essayé de scanner plusieurs personnages, avec un niveau de détail assez élevé. Le problème rencontré ici concerne justement le niveau de détail. Pour avoir un personnage articulé qui soit bien scanné, il faut que le maillage reproduise au plus près les détails des articulations. Il faut de plus que le maillage soit bien fermé, et 2-variété. Pour cela, il est nécessaire de le scanner avec un nombre de scan suffisant, et sous différents angles. Il est difficile de scanner un personnage articulé sous différents angles sans que celui-ci ne perde sa pose. Nous avons donc obté pour un personnage articulé, mais avec peu d'articulation. Ceci permet de le scanner de façon optimale. Par contre, on perd des degrés de liberté pour l'animation 3D. Ce qui fait que le nombre de mouvement est limité.
Fig 1. Utilisation du scanner
Le dernier gros problème concerne la qualité du scan. En effet, pour les utiliser ensuite, il est necessaire que les maillages soient simplifiés et 2-variété. Le problème vient du fait qu'on ne peut pas controler les propriétés du maillage via l'interface. L'alignement des différentes faces obtenues n'est pas toujours parfait, et compte tenu des différences de texture qu'on peut rencontrer sur les personnages, il y a souvent des "trous" dans le maillage. Il est donc difficile de pouvoir utiliser les scans obtenus sans procéder à un traitement supplémentaire, à l'aide d'autres logiciels.
Résultats
Nous vous présentons ci-dessous le résultat de nos scans. Certains de ces modèles seront réutilisés ensuite.
Pour commencer, nous avons voulu scanner un objet avec peu de relief et une forme simple. Il faut quand même que l'objet est un certain niveau de détail afin que l'alignement des scnas se fasse normalement. Nous avons prit une balle de baseball.
Fig 2. Résultat du scan d'une balle de baseball en mode texture, et en mode maillage.
Le rendu de ce scan est de bonne qualité. Le logiciel est arrivé, grace aux petites détails comme les coutures, à aligner automatiquement les différentes prises. Mais ce genre d'objet ne peut être utilisé pour notre projet. Nous avons donc aussi scanné des personnages articulés. Commençons par oscar :
Fig 3. Oscar pose pour nous ("Waouh, il est très souple oscar !!!")
Oscar fait partie de ces bonhommes qu'il est difficile de scanner parce qu'ils ont beaucoup d'articulations. Lorsqu'il prend la pose, il a du mal à la tenir pendant tout le temps du scan. De plus, lorsque certaines zones sont dans l'ombre du scanner, il faut refaire des scans en changeant la normale des faces. Il est encore plus difficile pour Oscar de tenir la pose ... Nous n'avons donc pas réussi à prendre Oscar pour plusieurs poses. Mais en voici une :
Fig 4. Résultats pour Oscar avec le logiciel du scanner, puis sous Blender
Compte tenu du nombre d'articulations et de la façon dont elles sont visibles sur Oscar, nous n'avons pas pu obtenir un maillage fermé (donc encore moins un maillage 2-variété). Nous n'avons donc pas pu utiliser Oscar comme modèle pour l'animation. Un second modèle a prit sa place : Sanosuké.
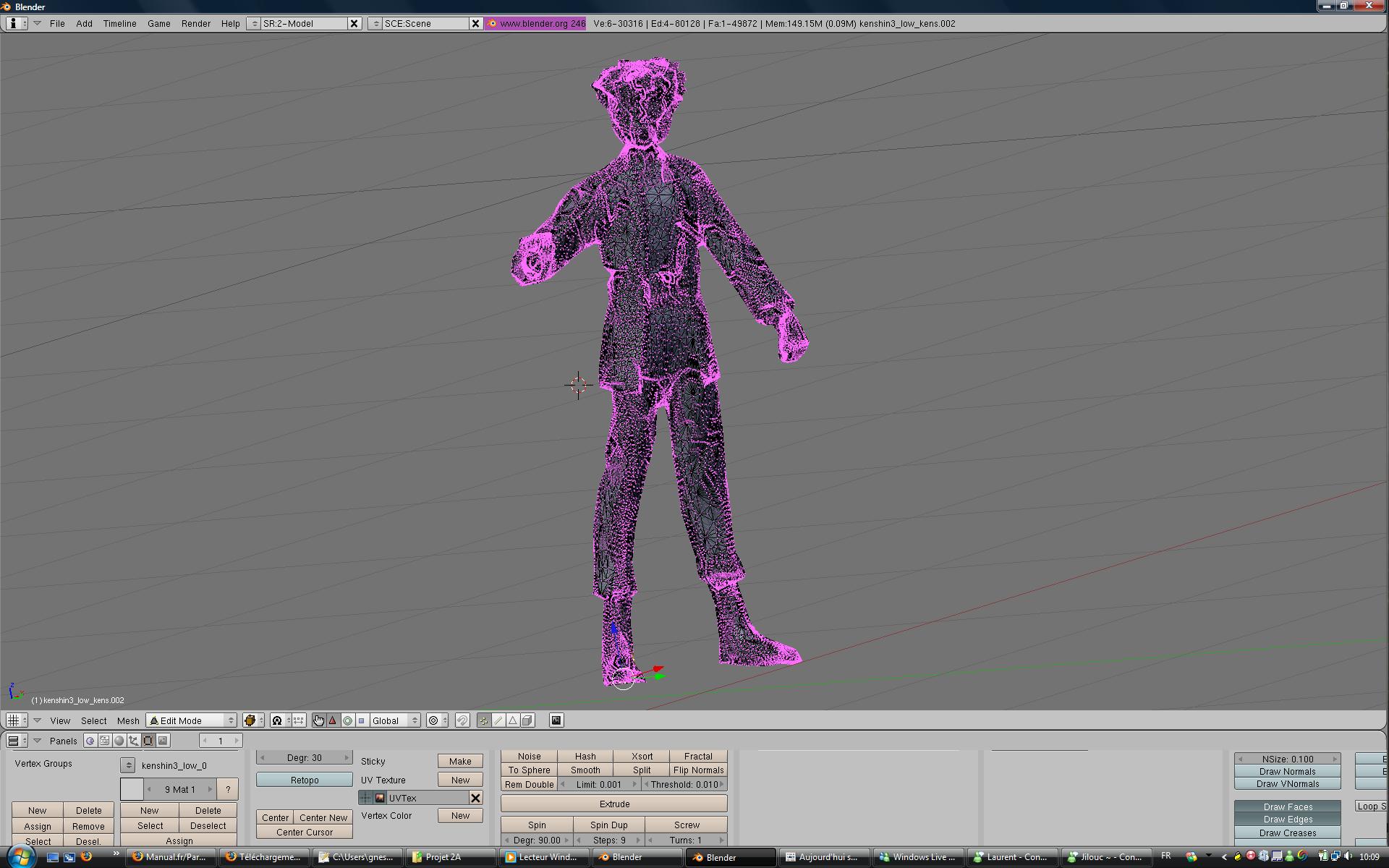
Fig 5. Résultats pour Sanosuké avec le logiciel du scanner, puis sous Blender
Ce modèle est peu articulé, mais juste assez pour nous. Nous allons donc l'utiliser par la suite, avec d'autres modèles qui ne sont pas des scans, mais des modèles déjà définis virtuellement. Pour l'utiliser ensuite, il est nécessaire qu'il soit fermé et 2-variété. Nous avons dû effectuer un travail supplémentaire sur le maillage grace à Blender. En effet, le maillage n'était pas 2-variété. Certaines faces et certains noeuds étaient doublés. De plus, les faces n'étaient pas toutes triangulées. Une fois que toutes ces opérations ont été effectuées, nous pouvons utiliser le maillage pour nos calculs.
Phase de recherche
La première partie du projet nous a amené à faire des recherches afin de trouver une façon de procéder. Nous avons pour cela lu plusieurs articles (voir bibliographie) afin de nous faire une idée des différentes façons d'appréhender le sujet. Ces articles nous ont donné plusieurs idées, avec leurs points positifs, et négatifs. Nous les détaillons en partie ci-dessous.
Transformations directes
Nous avions pensé à deux transformations directes différentes. La première est basée sur l'analyse des topologies des deux maillages utilisés. La deuxième ne tient plus compte des différences de topologie et se base entièrement sur une analyse des volumes.
Transformation directe du maillage
Nous partons du principe que nous avons deux maillages représentant le même objet dans deux positions différentes. Nous avons alors pensé à faire le morphing directement sur le maillage. Le problème vient du fait que les deux maillages n'ont pas tout à fait la même topologie.

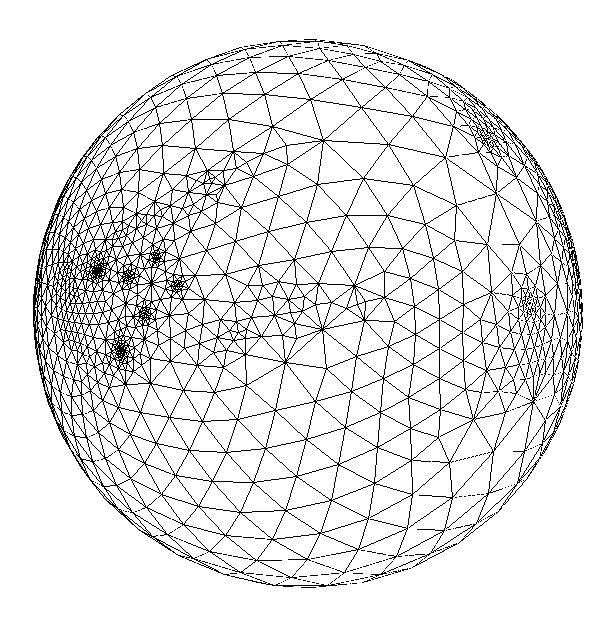
Fig 6. Exemple de projection d'une vache sur la sphère unité
L'idée serait alors de faire une projection sur la sphère unité des deux maillages, et d'effectuer le morphing à ce niveau-là. Cette projection permet de simplifier le problème de la différence des topologies. Il est plus facile d'unifier les topologies sur un espace plus simple. Mais le problème des topologies reste quand même complexe.
Transformation basée sur un calcul de volume
Le principe de cette transformation repose sur la voxelisation des deux maillages. Les différences de topologies ne présentent alors plus un problème. Le problème vient de la difficulté à convertir les maillages en volume.
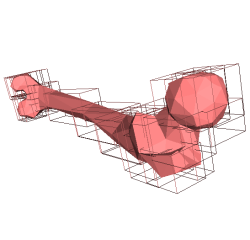


Fig 7. Exemple de voxelisation extrait du Projet Image 2005 de G. Aujay et M. Tournier
Le détail du principe de mise en volume est décrit dans [LGL95], ainsi que dans le compte rendu du Projet Image 2005 : Voxelisation d'une scène polygonale.
Transformations indirectes
Ici, la transformation ne s'applique pas directement au maillage, mais à un intermédiaire qui nous permet ensuite de recalculer le maillage.
Utilisation d'un exo-squelette
Le principe est de construire un exo-squelette autour des points du maillage. Ce procédé repose sur un calcul d'interpolation des points à partir de cette structure. Le problème principal problème est celui des comparaisons des topologies. Nous avons donc obté pour une solution ne faisant pas appel à un calcul de topologie.
Skinning
Le principe du skinning (cf. [TVD06]) se rapproche de celui de l'exo-squelette. La différence est que le squelette calculé se rapproche plus du squelette anatomique de l'objet. A partir de ce constat, nous avons décidé de nous concentrer sur des objets articulés de type être vivant. En effet, calculer le squelette d'une balle de baseball n'a pas de sens.
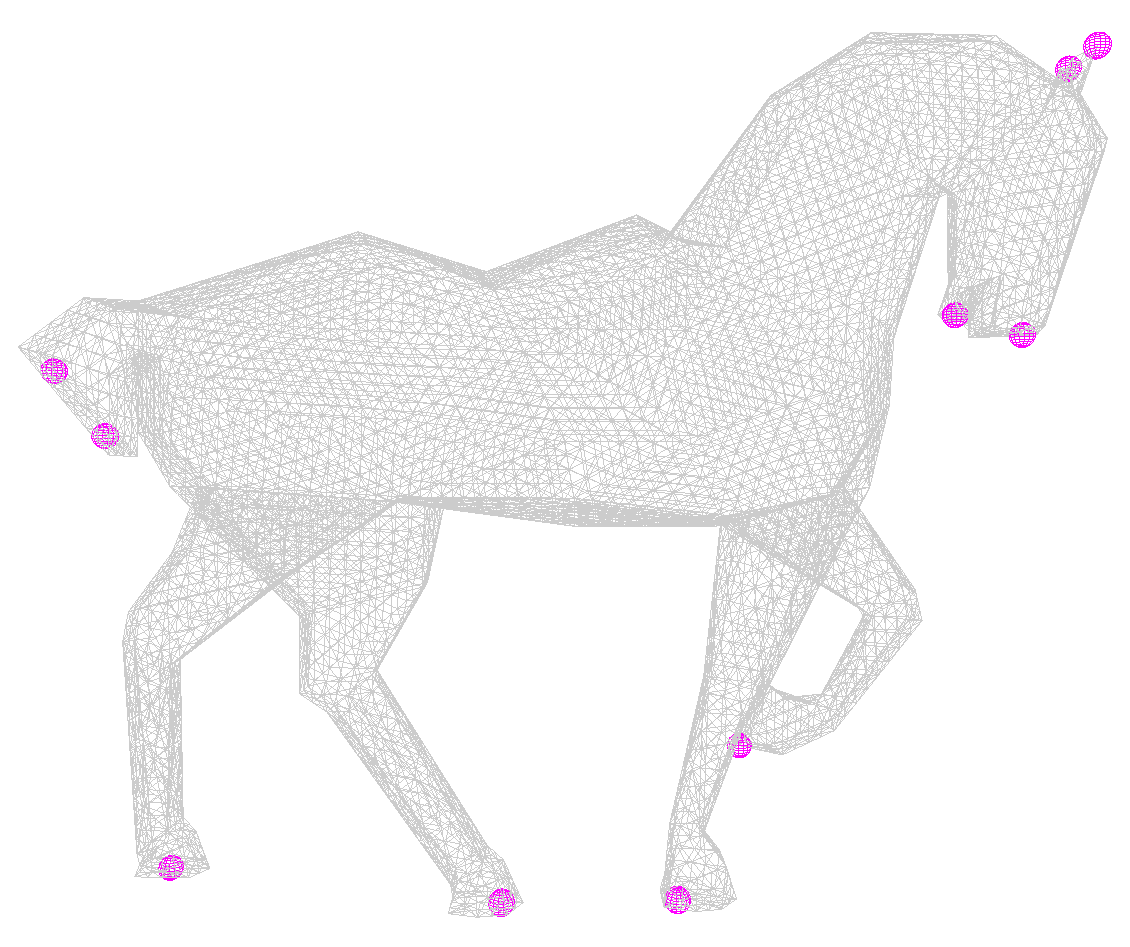
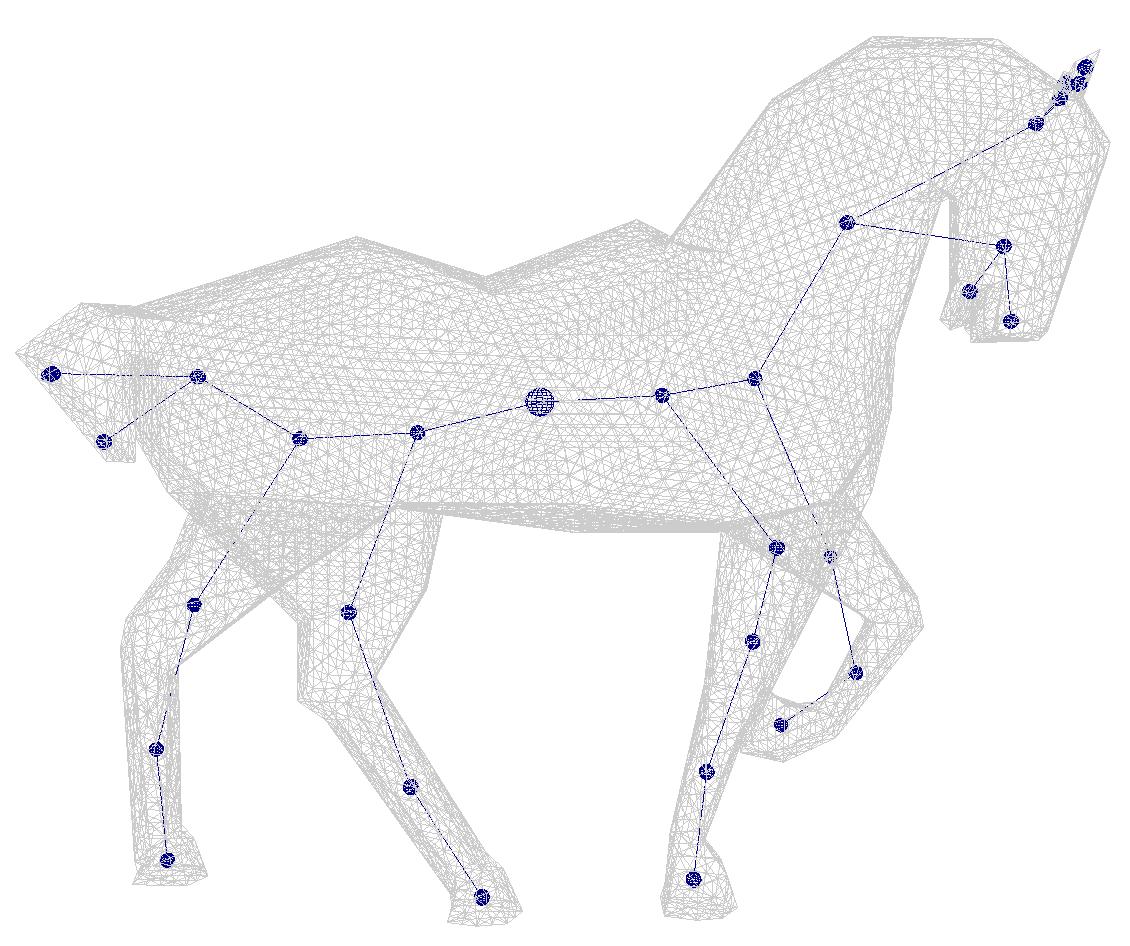
Fig 8. Exemple de calcul de squelette avec les graphes de Reeb
Le calcul du squelette se fait à partir des graphes de Reeb et d'une fonction de Morse. La méthode de calcul est détaillée ci-dessous.
Algorithme de création du squelette
Pour calculer le squelette à partir du maillage 3D obtenu par le scanner, nous avons utilisé l'algorithme de création de squelette conçu par Grégoir Aujay, Franck Hétroy et Francis Lazarus dans [AHL06]. Le principe est le suivant :
A chaque point du maillage, on fait correspondre la valeur d'une fonction
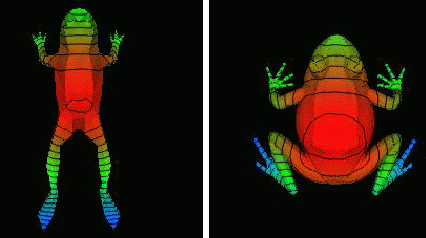
Fig 9. Exemple d'une fonction de Morse sur un modèle de grenouille
Maintenant que nos sommets sont "décorés", nous allons créer le graphe de Reeb. Le graphe de Reeb associe aux iso-f (courbe sur le maillage de même valeur de la fonction de Morse) de gradient nul un point sur le graphe.
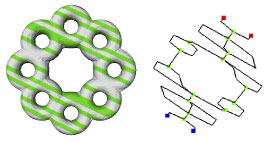
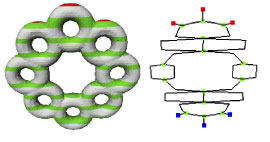
Fig 10. Exemples de deux graphe de Reeb pour des fonctions de Morse différentes sur le même maillage
On doit maintenant créer un squelette à partir de ce graphe de Reeb. Pour cela, on place les "os" du squelette au centre des iso-f et on va supprimer les noeuds inutiles. On va aussi chercher à détecter les symétries possibles du graphe.
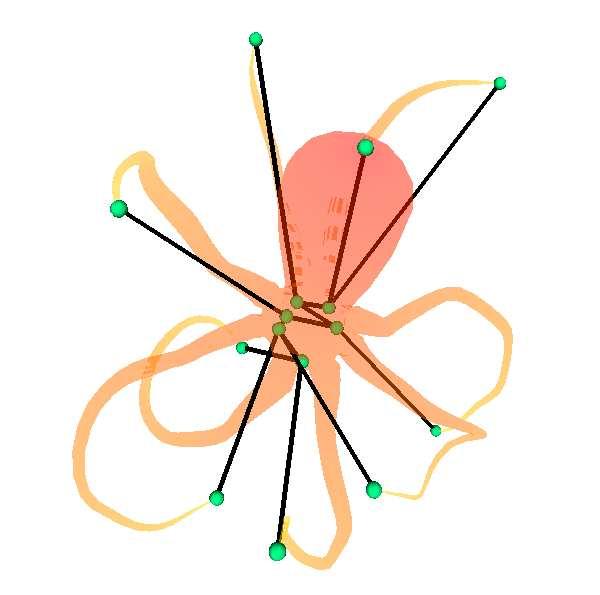
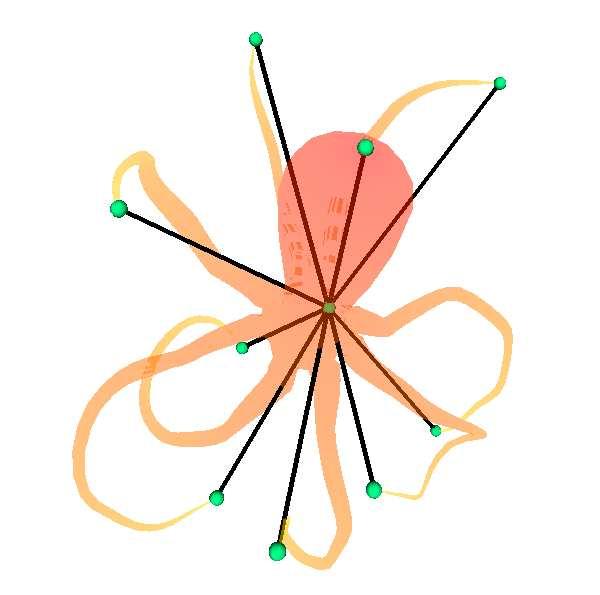
Fig 11. Passage d'un graphe de Reeb à un squelette
Pour notre projet, nous avons utilisé le code source de Grégoire Aujay qui permet de créer des squelettes. Pour pouvoir l'inclure dans notrre travail, il a fallut recoder le programme en utilisant la librairie OpenMesh (le code de Grégoire Aujay étant en CGAL).
Matching entre deux squelettes
La mise en correspondance des squelettes se fait en plusieurs étape. Le but est de rassembler un maximum d'information sur la structure du graphe. On pourra ainsi caractériser les éléments le constituant les ranger dans des catégories morphologique pour un matching plus pertinent.
Calcul des attributs topologiques du graphe
La première étape est plutôt simple. On commence par calculer, pour chacun des sommets du squelette, un ensemble d'attributs permettant de décrire sa position dans le graphe. Le squelette est un arbre, on peut donc partir d'une racine, lui associer une arborescence et calculer :
- le nombre de fils directs
- le nombre de feuille du sous-arbre
- le nombre de sommets du sous-arbre
- la profondeur
pour chacun des sommets de l'arbre. Ce calcul se fait de façon très simple avec un algorithme récursif.
Recherche de structures morphologiques
Nous allons commencer par définir de façon intuitive puis formelle les structures susceptibles de se trouver dans un arbre représentant un squelette comme celui-ci :
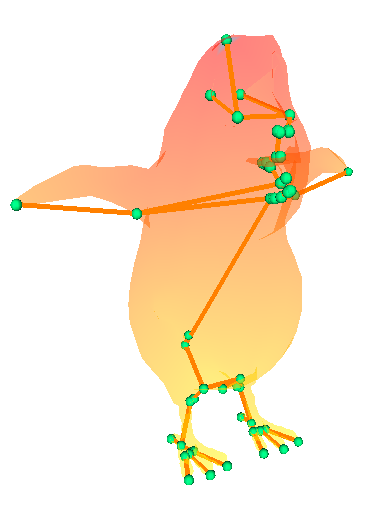
Fig 12. Image d'un squelette
On peut repérer certains éléments type de la morphologie des être articulés (vertébrés). Notamment : une colonne vertebrale, des membres, des mains, une tête :
- La tête : La tête est le sommet qui sert de point chaud à la construction du graphe.
- Les mains, les doigts et les coudes : Une main est une extremité du corps composées de doigts et reliée au reste par un coude. On appelera donc main tout sommet dont tous les fils sont des feuilles de l'arbre. Ces fils sont les doigts associés à cette main. Le ou les coudes sont les sommets sur le chemin qu'on peut construire en remontant les sommets pères de la main jusqu'à la colonne vertebrale.
- Les membres : Un membre est défini comme étant une feuille de l'arbre qui n'a pas été associée à une main. Font partie du même membre tous les sommets du chemin qu'on peut construire de la même façon que les coudes d'une main en partant de cette feuille.
- La colonne vertebrale : C'est le plus long chemin qu'on peut construire de façon déterministe en partant de la tête en descendant le long du corps sans passer par des membes ou des coudes. Autrement dit, on part de la tête, tant que le sommet courant n'a qu'un seul successeur, on ajoute celui-ci à la colonne, s'il a plusieurs successeurs, on éliminé ceux qui sont des coudes ou des membres, s'il n'en reste qu'un on continue, sinon on arrête.
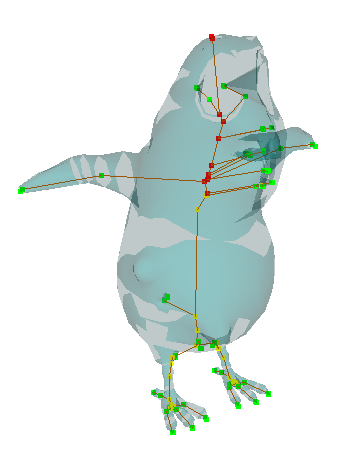
Fig 13. Image d'un squelette avec une structure colorée correspondant aux différents membres.
Les éléments de chacune des structures possèdent deux indices. Un indice qui permet d'identifer le numéro de la structure à laquelle ils appartiennent et un indice qui donne leur ordre d'apparition au sein de la structure. Ce dernier est important car il faut mettre un ordre sur les éléments d'une même entité pour le matching. Par exemple, les doigts d'une main doivent être numérotés pour pouvoir être associés aux doigts de la même main sur l'autre squelette. Ce numéro peut être calculé de différentes façon. Celles que nous avons retenues sont l'ordre par rapport à la valeur de la fonction de Morse ou par rapport à une direction spatiale (l'abscisse par exemple).
Matching
Maintenant qu'on est passé à un niveau d'abstraction supérieur en adoptant une description morphologique des squelettes, il est relativement facile les mettre en correspondance en utilisant les structures qu'on a calculées dans la partie précédente. La colonne vertebrale de l'un correspond à la colonne vertebrale de l'autre, les mains de l'un correspondent aux mains de l'autre et de même pour les membres et la tête.
Un certains nombres de problèmes se posent alors. Nous n'avons pas su tous les résoudre de façon systématique mais nous avons trouvé des idées (des heuristiques) pour certains cas.
Les colonnes vertébrales n'ont pas toujours le même nombre de sommets.
Les colonnes vertebrales sont des chemins dans l'arbre. Pour les matcher, on les parcourt dans le même sens en cherchant pour chaque sommet le plus proche (par rapport à la valeur de la fonction de Morse) dans l'autre colonne quitte à "sauter" des sommets et sans jamais repartir dans le sens inverse.
Si on a plusieurs mains ou membres, comment savoir lesquelles vont ensemble ?
Ces structures sont toujours attachées à la colonne vertebrale. On considère donc qu'on peut les associer s'ils sont attachés à des sommets correspondant des colonnes. S'il y a plusieurs mains ou membres sur le même sommet de la colonne, on peut les numéroter par rapport à un critère (direction spatiale, valeur de la fonction de Morse ...).
Plus le nombre de sommet du squelette est important, moins le matching est efficace.
Nous utilisons une technique de multi-résolution pour tirer avantage de l'efficacité de l'algorithme sur des squelettes simples. On commence par faire un matching avec un nombre de sommets assez faible. On recalcule ensuite un squelette avec un nombre de sommets plus important pour lequel on réapplique l'algorithme. Pour les structures qui n'ont pas pu être mises en correspondance, on utilise les informations du premier matching - par exemple on sait qu'un membre peut-être associé à tel autre, ...
Comment choisir automatiquement un bon nombre de sommets pour les squelettes ?
Nous avons utilisé la stratégie suivante : Pour les squelettes définitif qui serviront au second matching, on cherche le plus grand nombre de sommets pour lequel l'algorithme réussit à tous les associer à une structure morphologique. Pour le squelette simple, qui servira au premier matching, on cherche le nombre de sommets plus petit que le précédent qui minimise le nombre de sommets non matchés par l'algorithme.
Malgrè tout il reste des sommets non matchés.
Avoir des sommets statiques dans l'animation de squelettes peut saboter le résultat. Si certains sommets ne suivent pas le mouvement local du squelette, ceci donne une déformation abberante pendant l'animation. Pour minimiser ce genre d'erreur, on dira que chaque sommet non matché aura un mouvement pendant l'animation qui correspondra à la moyenne des mouvements de ses voisins.
Morphing entre deux squelettes
Comme nous avons décidé d'utiliser le skinning, nous appliquons la déformation sur le squelette calculé plus haut. Pour cela, nous avons décidé dans un premier temps d'appliquer une transformation linéaire. Nous regardons les points ayant bougé entre les deux squelettes, et nous calculons le vecteur de déplacement entre les deux. Nous calculons ensuite les squelettes intermédiaire en spécifiant le nombre de squelettes voulu. Ci dessous un exemple d'animation sur le squelette de l'oiseau du film Big Buck Bunny.
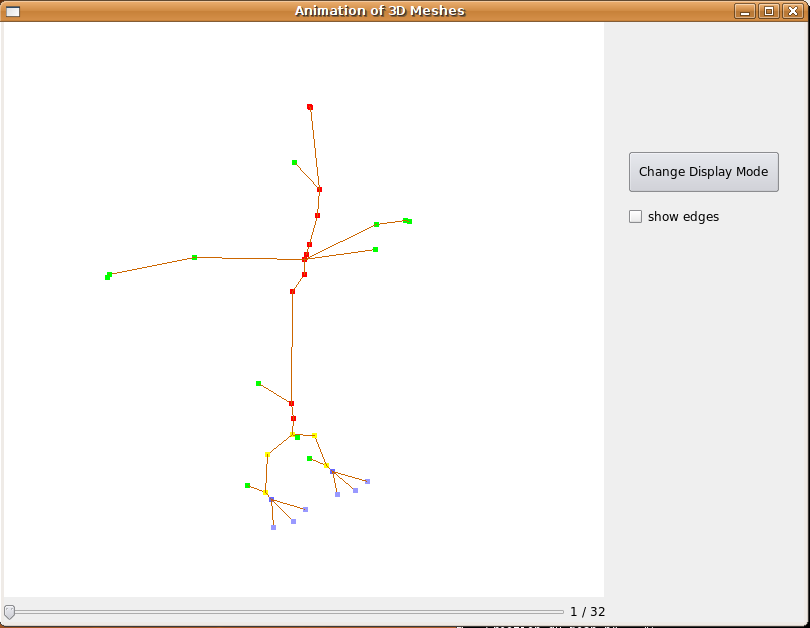
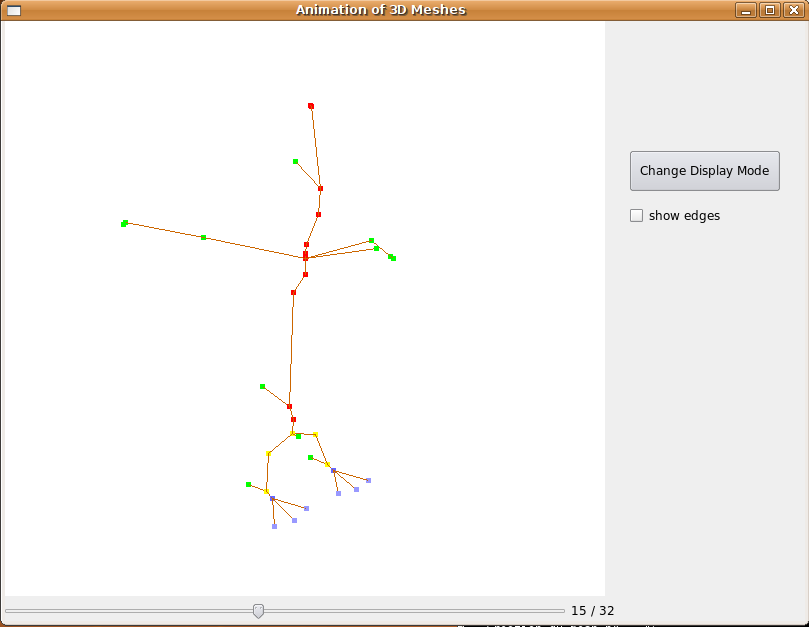
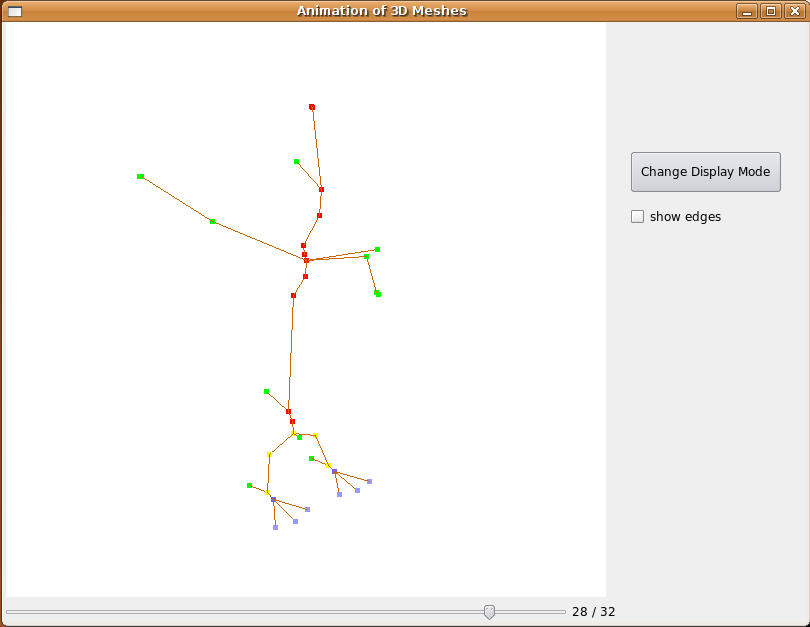
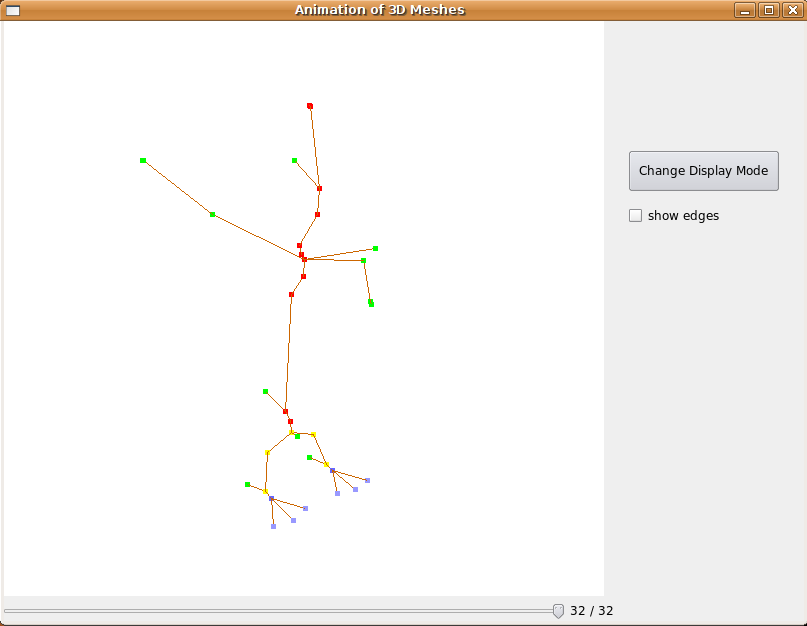
Fig 14. Quelques squelettes intermédiaires pour l'animation
Nous avons pas eu le temps de changer le mouvement, mais nous pensons qu'il faudrait, à terme, utiliser une autre forme de mouvement pour le squelette afin de rendre l'animation plus réaliste. Si nous partons du principe que les os qui se correspondent dans les deux squelettes sont de même longueur, il faudrait calculer l'arc de cercle dans l'espace qui relie les deux noeuds correspondant, et utiliser une ligne polygonale entre les deux pour faire le mouvement. Le problème est que, dans la plupart des cas, les deux os n'ont pas là même longueur. L'idée serait alors de procéder comme s'ils avaient la même longueur pour le calcul de l'arc de cercle, puis de faire une réduction linéaire de la longueur de l'os. Le mouvement serait alors plus fluide, et donc, bien plus réaliste
Amélioration de l'interface
Pour pouvoir afficher l'animation et la construction du squelette nous avons codé une petite interface. Cela nous à permit d'utiliser la librairie QGLViewer et la librairie Qt
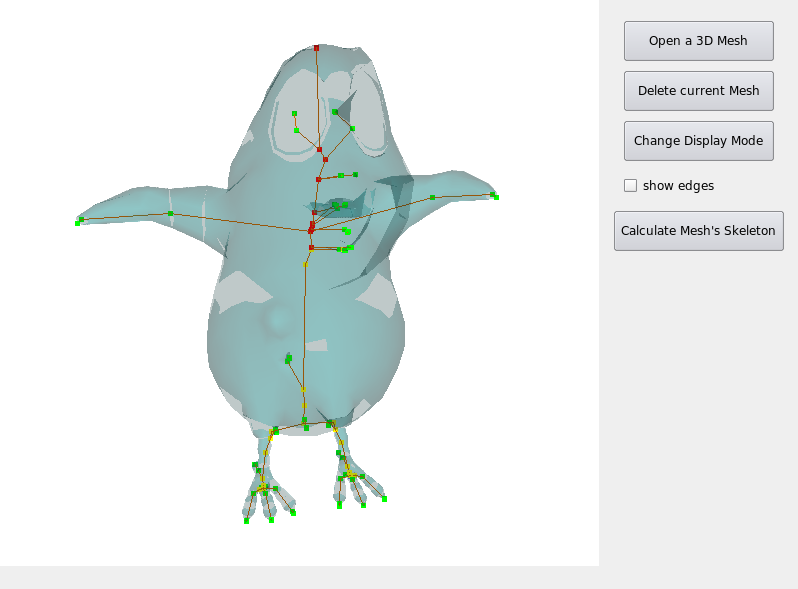
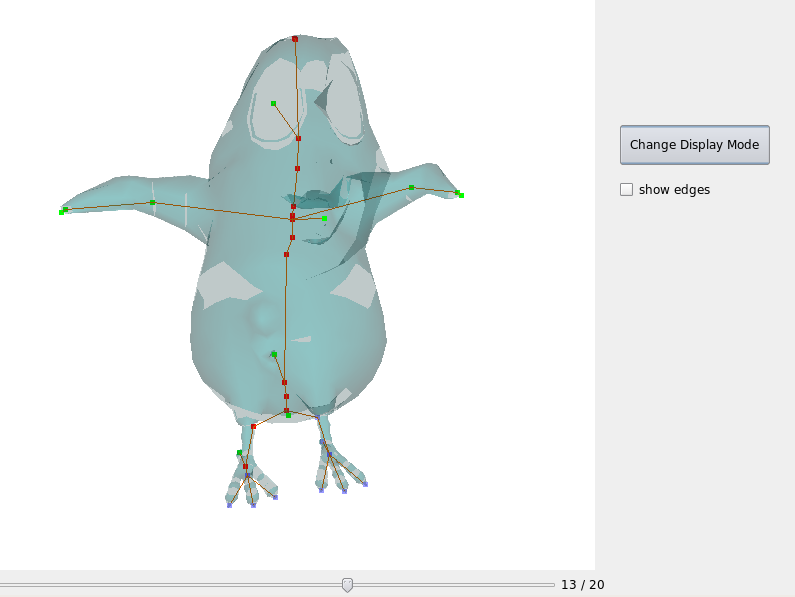
Fig 15. Aperçu de l'interface
Résultats
Nous présentons ci dessous quelques résultats obtenus grâce à notre programme.
Le premier aperçu montre l'oiseau utilisé avec son squelette. Le squelette n'a pas encore été raffiné. Le calcul du squelette se faisant de manière automatique (nous ne précisons pas, à part la tête, la position des points caractéristiques), nous pouvons remarquer les arêtes allant dans le bec. Nous remarquons aussi qu'il y a différentes articulations sur la colonne vertébrale. La position de ces noeuds est importante.
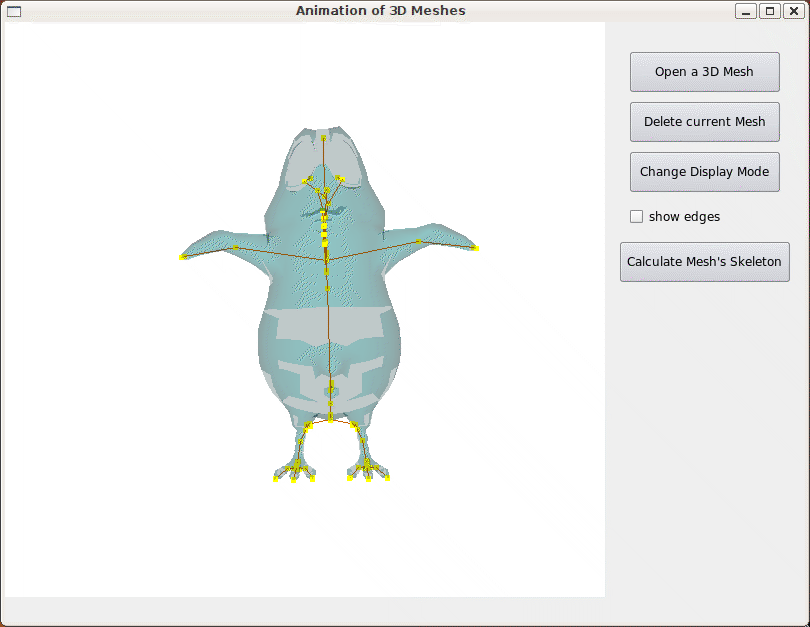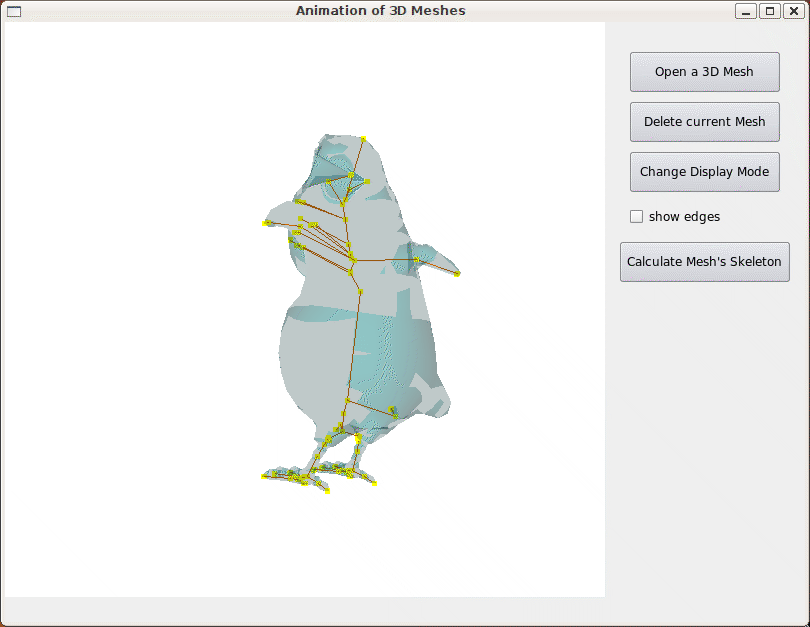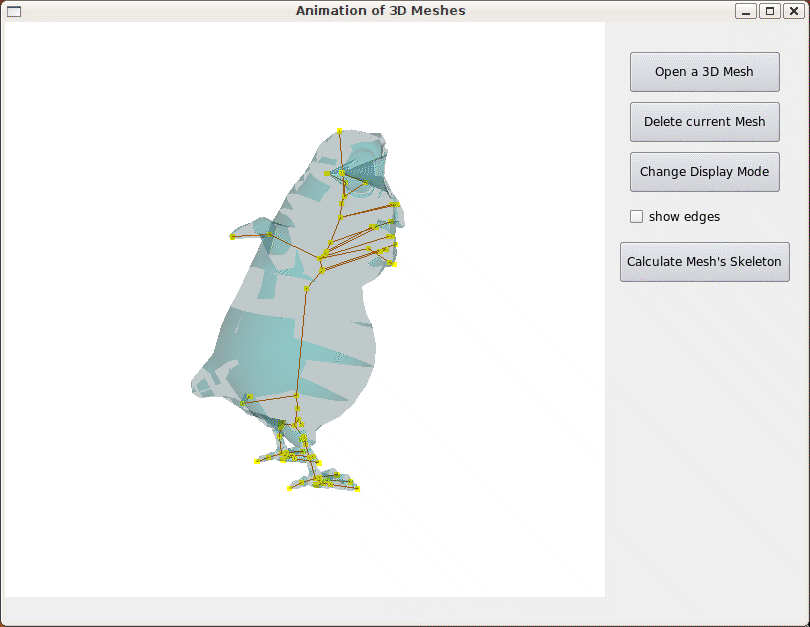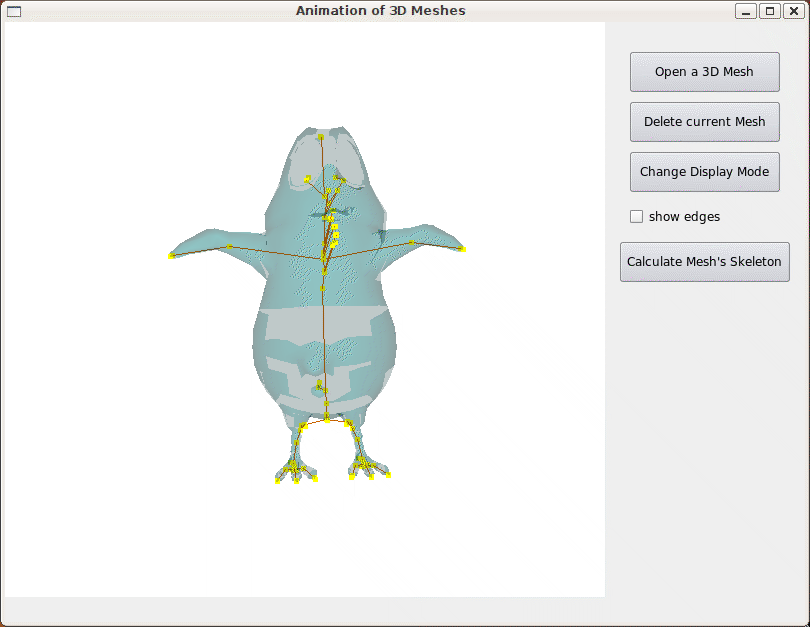
Fig 16. Aperçu du rendu après calcul du squelette.
Lorsque nous voulons calculer l'animation entre deux positions du modèle, nous donnons à l'interface deux fichiers .OFF contenant les deux maillages. Nous calculons les squelettes des maillages, et nous faisons l'animation à partir du squelette. L'animation ci-dessous présente un cas pour lequel notre algorithme est assez peu fonctionnel.
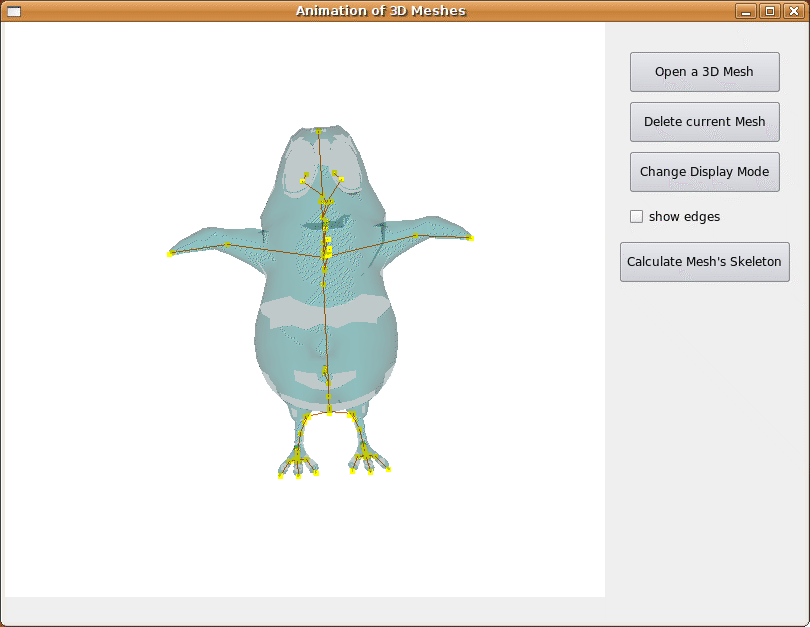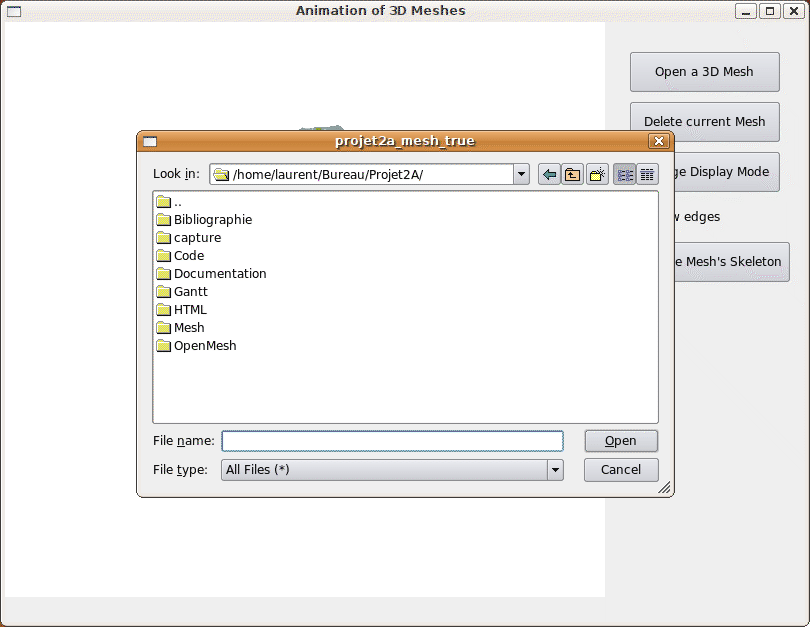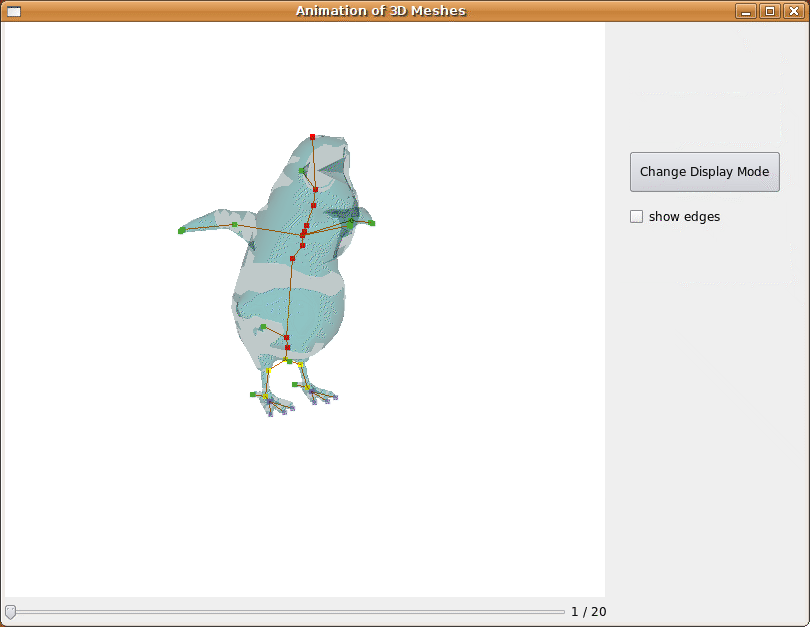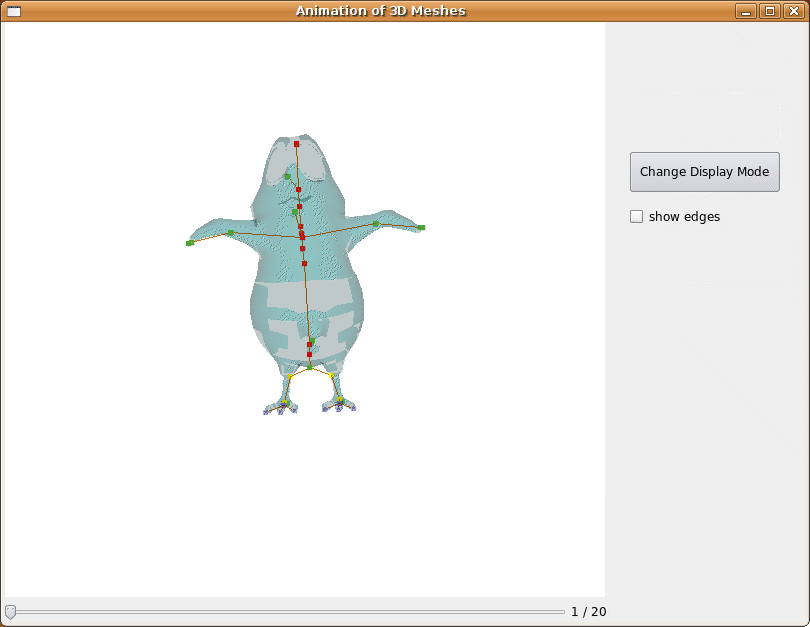
Fig 17. Aperçu du rendu pour deux positions assez éloignées.
Nous remarquons que la première chose que fait le programme est de raffiner le squelette. De cette façon, on limite les erreurs commises dans l'animation. Mais certains points, qui ne sont à priori pas impliqués dans l'animation peuvent être matchés, et ne pas être exactement à la même place dans le squelette. Le mouvement des points du maillage étant calculé en fonction du mouvement des articulations et des os, il y a un effet papillon sur l'animation. La somme des mouvements annexes devient de plus en plus génante au fur et à mesure que le mouvement s'effectue. Ce qui fait que sur ce genre de mouvement, le résultat est assez médiocre.
Dans l'exemple suivant, le mouvement est de petite ampleur. Le résultat est donc meilleur. On peut aussi apprécier de façon plus précise l'influence sur l'animation des erreurs commises par le calcul de squelette totallement automatique.
Fig 18. Aperçu du rendu pour deux positions assez proches.
Nous avions choisi de faire nos calculs de façon automatisée. Nous nous sommes donc rendu compte que le calcul de squelette n'était pas satisfaaisant pour avoir une animation correcte. Deux solutions pourraient s'offrir à nous : trouver un autre algorithme de calcul de squelette plus précis, ou laisser tomber l'automatisation du calcul. La deuxième solution ferait perdre un peu d'intérêt au sujet.
Il reste aussi un problème non négligeable pour le matching de squelettes. En effet, le calcul du matching se fait avec des heuristiques qui ne marchent que dans certains cas. Il faudrait donc pouvoir généraliser ce principe.
Impressions sur le projet
Ce projet a été très intéressant. C'est une bonne première expérience en réalité virtuelle (pour deux d'entre nous, l'autre ayant déjà travailler sur des maillages 3D pour son TER). Cela nous a permis d'utiliser plusieurs librairies utiles au traitement des maillages 3D. Nous retiendrons que CGAL permet de faire plus de chose qu'OpenMesh. Cependant, les primitives d'OpenMesh nous ont suffit pour notre projet. Nous retiendrons aussi que la documentation disponible pour OpenMesh est un peu légère. Nous avons donc mis un certain temps avant de pouvoir utiliser l'algorithme de calcul de squelettes sous OpenMesh.
Nous avons tout fait pour finir le projet, et pour pouvoir présenter des résultats complets. Pour cela, nous n'avons pas pu optimiser les calculs et le rendu. Nous en concluons que notre résultat est un premier jet, mais qu'une ou deux semaines de plus nous auraient permis de nous pencher sur des détails de l'implémentation. Nous avons déjà parlé du morphing de squelettes, mais d'autres problèmes persistent.
Nous n'avons pas pu utiliser les personnages que nous avons réussi à scanner. En effet, le Sanosuké présenté plus haut déclenche un arrêt du programme. Nous n'avons pas eu le temps de regarder pourquoi, mais nous pensons que le problème vient du calcul de squelettes. Nous pensions que les maillages scannés seraient plus facilement utilisables pour les calculs. Nous aurions donc dû passer plus de temps sur le traitement des maillages scannés.
Finalement, nous retiendrons que le projet été vraiment intéressant, avec une grosse part de recherche. Le manque de temps est peut être dû au fait que nous étions assez libre dans la mise en place du cahier de charges, et de ce fait, nous avons peut être passé trop de temps sur la reflexion du début. Nous savions dès le début que le code n'était pas le plus important, mais il représente pourtant une grande partie du travail. Rappelons aussi que la première semaine a été consacrée aux soutenances de TER et de CECA, ce qui a fait que nous avons vraiment commencé le projet le lundi de la deuxième semaine.
Layout de cette page web utilise le stylesheet de l'équipe "Antoine MELER & Adrien BERNHARDT" de l'année 2006.
top