Présentation de notre algorithme
Segmentation
Cette première partie consistait à découper le maillage animé en k parties approximativement rigides.
Pour déterminer les k clusters, il faut utiliser l points prélevés dans le mesh. Ces l points représentent le "centre" des régions obtenues par l'algorithme Varshape Approximation à un temps de référence t=0. Nous avons pu réaliser cette étape en intégrant le projet de Damien Rumiano et Emile de Weerd puis en utilisant leur algorithme. Cependant, au delà de la compréhension de leur algorithme, nous avons dû ajouter des méthodes et des structures de données pour prélever les informations qui nous sont utiles en sortie de leur algorithme.
Une fois les coordonées des l points prélevées pour t=0, il a fallu récupérer les coordonnées de ces points pour chaque frame en parcourant méthodiquement le fichier .WRL.
Pour résumer cette étape, on échantillone l points du mesh et à chaque triangle est affectée une zone à l'aide du Varshape Approximation. L'étape suivante permet de réunir ces l zones en k clusters cinématiquement rigide.
Nous avons donc implémenté une fonction qui prenait un nuage de points animés, et qui retournait la répartition des points entre les différents clusters. Pour cela, nous nous sommes appuyés sur un article de Ng, Jordan et Weiss intitulé On Spectral Clustering: Analysis and an algorithm. L'algorithme en question s'appuyait sur la méthode des k-means, appliquée à des points en dimension k obtenus après diverses transformations de la matrice d'affinité du nuage de points. L'algorithme concernait un nuage de points statique : c'est pourquoi nous avons eu à le modifier pour pouvoir l'appliquer à un nuage de points animé. Ainsi, il a fallu générer une matrice d'affinité différente, qui prenait en compte l'évolution des points, les moyennes et écarts-types de leurs distances mutuelles au cours du temps.
Topologie
Nous parcourons pour déterminer l'adjacence des clusters les triangles du mesh puis nous regardons leur cluster et ceux de leurs voisins. S'il y'a une différence, les deux clusters en questions sont considérés comme voisins et les sommets du triangle sont ajoutés à la frontière entre les deux clusters. On calcule le barycentre de ces points pour déterminer l'articulation barycentrique qui est une première approximation des articulations retenues pour le squelette. Nous n'avons pas limité le nombre de clusters voisins possibles. En effet, dans la publication, il est question d'une heuristique visant à limiter les clusters voisins à deux pour le calcul des articulations.On a procédé différement en utilisant tous les voisins et en reportant le problème au calcul des articulations. En effet, on a observé que par exemple, dans le cas d'un personnage animé, le torse est cinématiquement articulé avec la tête et les deux bras. Nous n'avons donc pas voulu nous limiter à l'heuristique qui peut cependant améliorer le temps de calcul.
Articulations
Dans cette partie, on récupère en entrée les points échantillonnés et leur position au cours du temps. Ensuite, on calcule les matrices de transformation Mi,tr->t. Ces matrices permettent de calculer la position du cluster i au temps t, à partir de la position du cluster i au temps tr, c'est-à-dire que
Mi,tr->tpi,tr,n = pi,t,n
où pi,t,n est la position du ne point du ie cluster au temps t. Les matrices permettent de ramener les deux clusters (dont on veut étudier l'articulation qui les lie) à la position-référence d'un des deux clusters, afin de n'avoir comme inconnue à déterminer qu'une seule position (x,y,z) (au lieu d'une séquence de positions).
Une fois ces matrices obtenues, on minimise une formule spécialement élaborée pour ce problème par les auteurs de l'article. L'argument réalisant le minimum est la position de l'articulation que l'on étudie. Pour obtenir la position de l'articulation au cours du temps, il suffit de multiplier le résultat de la minimisation par .5*(Mi,tr->t+Mj,tr->t) où i et j sont les numéros des segments reliés par cette articulation. On obtient alors la position au cours du temps de toutes les articulations entre clusters contigus. Cependant, deux zones contiguës n'ont parfois pas besoin d'une articulation entre elles, car cela n'a pas de réalité cinématique.
Pour résoudre ce problème, nous n'avons pas suivi l'heuristique proposée car elle n'est pas efficace pour les clusters ayant plus de deux clusters cinématiquement voisins. Nous avons suivi une autre méthode proposée dans une publication citée dans l'article : élaborer un graphe des articulations et des clusters, et en extraire l'arbre couvrant de poids minimal (Automatic Learning of Articulated Skeletons from 3D Markers Trajectories de Edilson De Aguiar, Christian Theobalt et Hans-Peter Seidel, 2006). Cela permet de bâtir la hiérarchie des articulations et des os, utile pour la partie suivante.
Os
À ce stade de l'algorithme, on a obtenu les points d'articulation, mais les os qui les relient ne sont pas de longueurs constantes au cours du temps. C'est dû au fait que les parties rigides du maillage ne le sont qu'approximativement. Afin d'imposer à chaque os une longueur fixe, nous avons parcouru les articulations les unes à la suite des autres, en calculant à chaque fois la longueur optimale de l'os adjacent. La longueur optimale était obtenue en minimisant une fonction qui cumulait les écarts entre les longueurs d'os, et entre les positions des articulations. On obtient alors le squelette final, aux os de longueurs fixes.
Il s'agit ensuite de recréer l'animation, mais sous forme de modèle animé par squelette. Nous n'avons pas eu le temps d'implémenter cette fonction. Il s'agissait de définir une position de référence pour le squelette, et, pour chaque position, de calculer les angles d'Euler des rotations aux articulations à l'aide de l'algorithme CCD décrit dans l'article Multi-dimensional input techniques and articulated figure positioning by multiple constraints de Badler, Manoochehri et Baraff (1987).
Poids de skinning
Dans cette partie, que nous n'avons pas eu le temps d'implémenter, on attribue, pour chaque point du mesh, des "poids de skinning" c'est-à-dire que l'on calcule la dépendance de chaque point vis-à-vis des os voisins pour la déformation pendant l'animation. Ce calcul se fait via la résolution d'une équation de la chaleur, décrite dans l'article Discrete Laplacian Operators: No Free Lunch de Wardetzky, Mathur, Kaelberer et Grinspun (2007). Nous pensons que cela n'aurait pas été la partie du programme la plus difficile à implémenter, étant donné le nombre de publications à ce sujet. Ensuite il aurait fallu concevoir une fonction animant le mesh à l'aide du squelette en utilisant les paramètres d'animation calculés dans la partie "Os" et les poids de skinning. La documentation pour cette partie est tout aussi abondante, et l'implémentation aurait ainsi été sans difficultés. Les problèmes à résoudre auraient plutôt concerné les petits bugs à corriger (certainement ardus à débusquer), et l'optimisation du temps de calcul.
Résultats obtenus
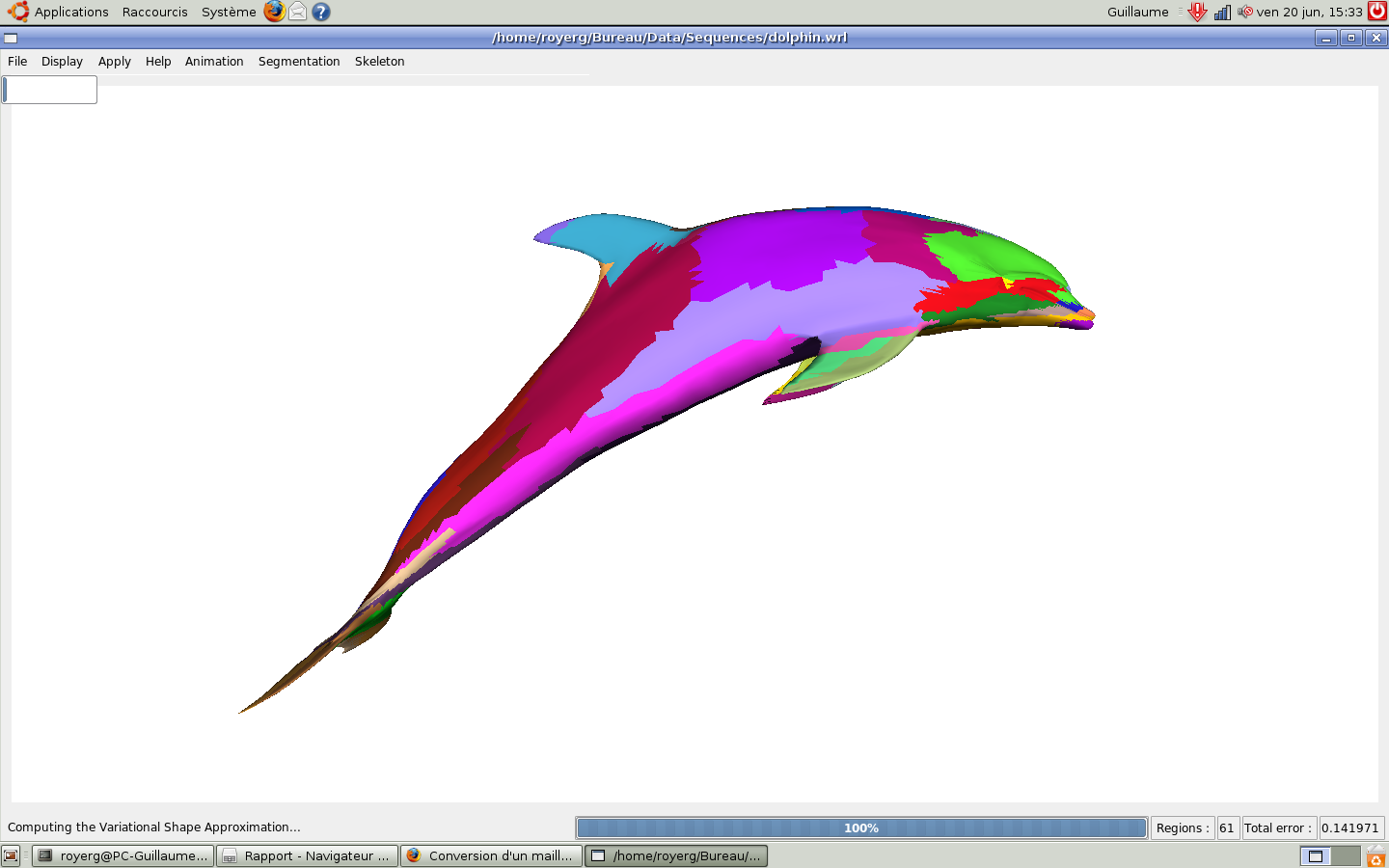
Nous observons l'ensemble des résultats avec le dauphin animé. La première étape que l'on observe est l'application du VSA sur t=0. On demande en nombre de régions 1% du nombre de sommets.
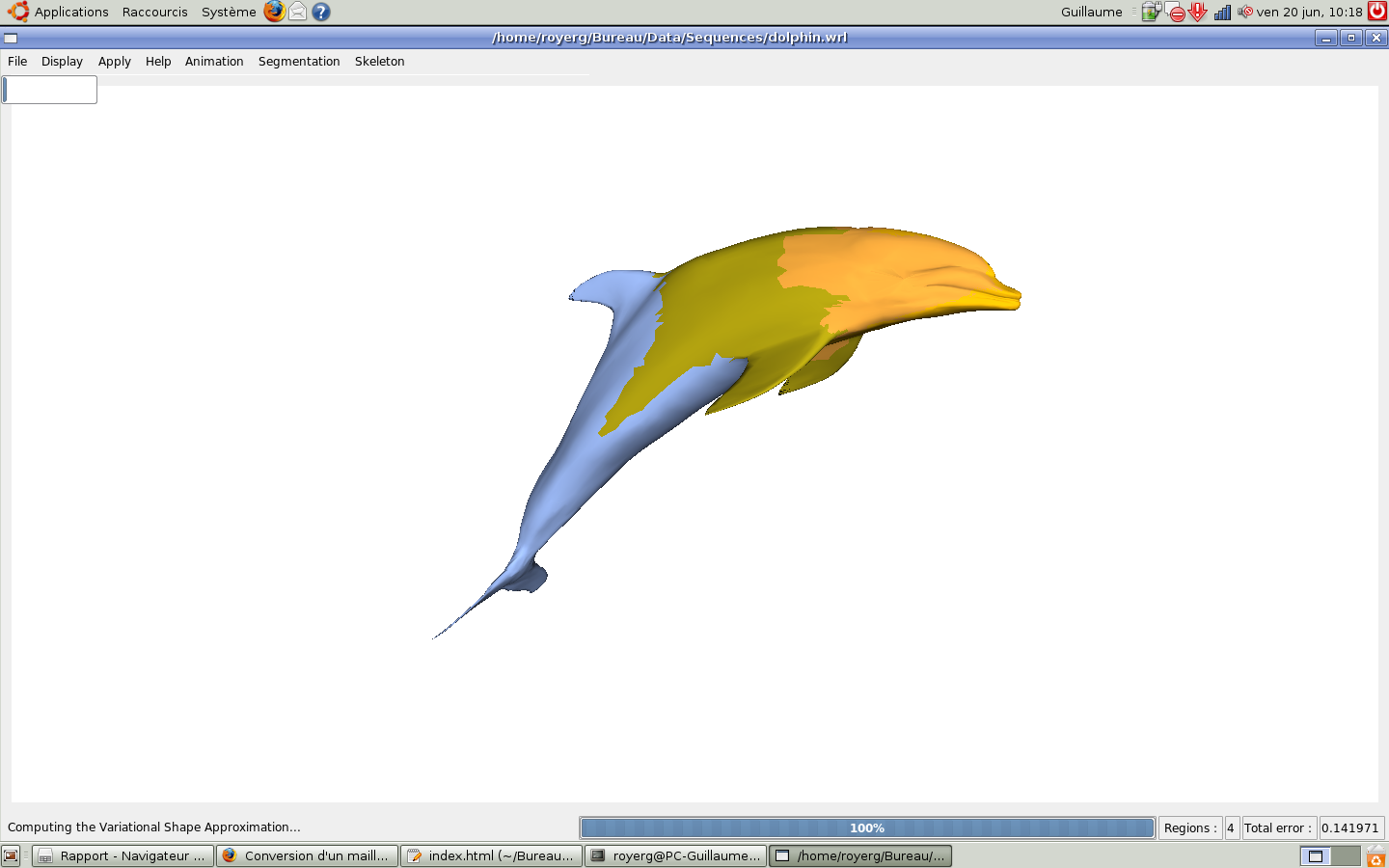
On applique ensuite l'application des clusters : les régions se regroupent par régions rigides dans l'animation. (ici avec k=4 clusters)
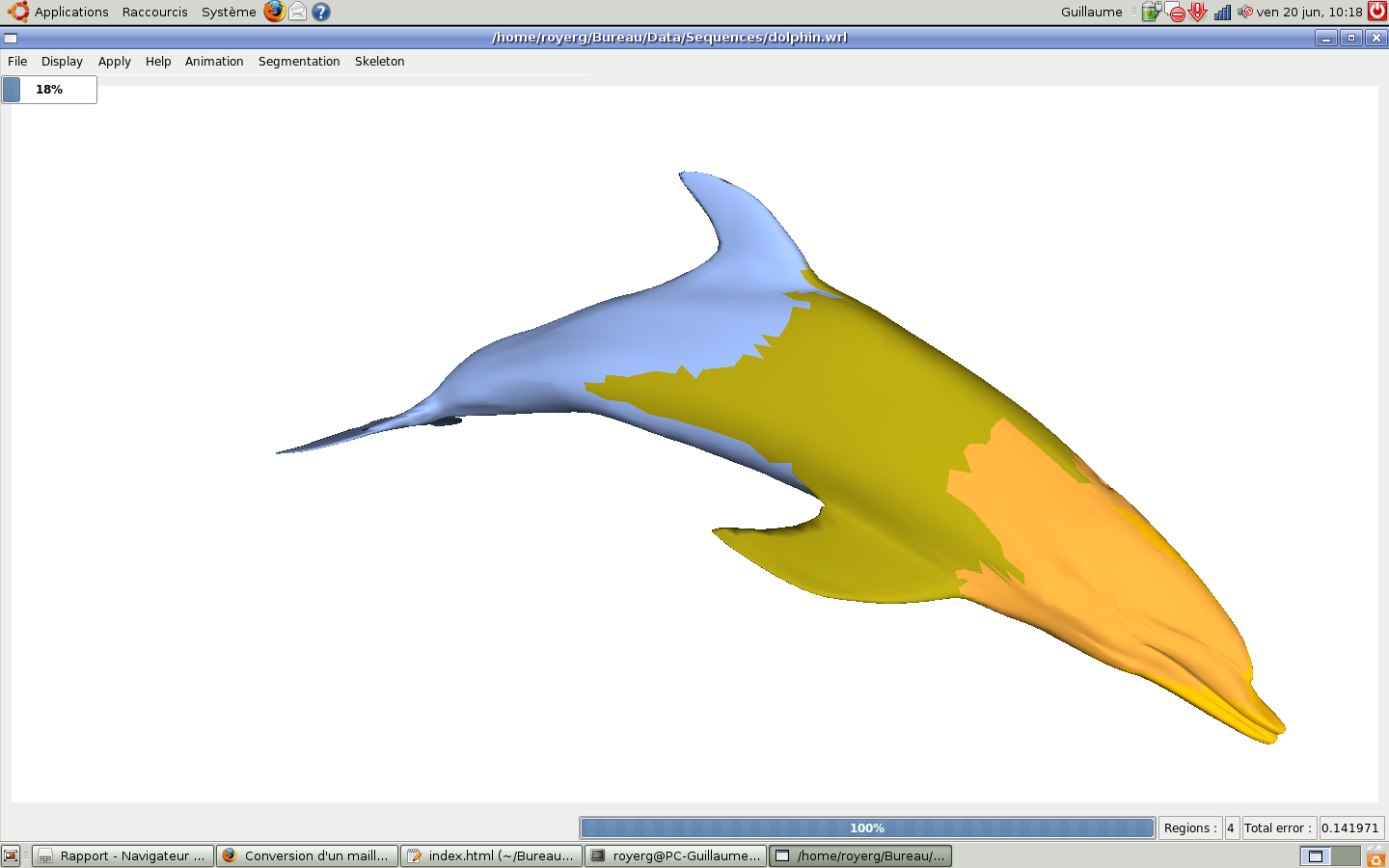
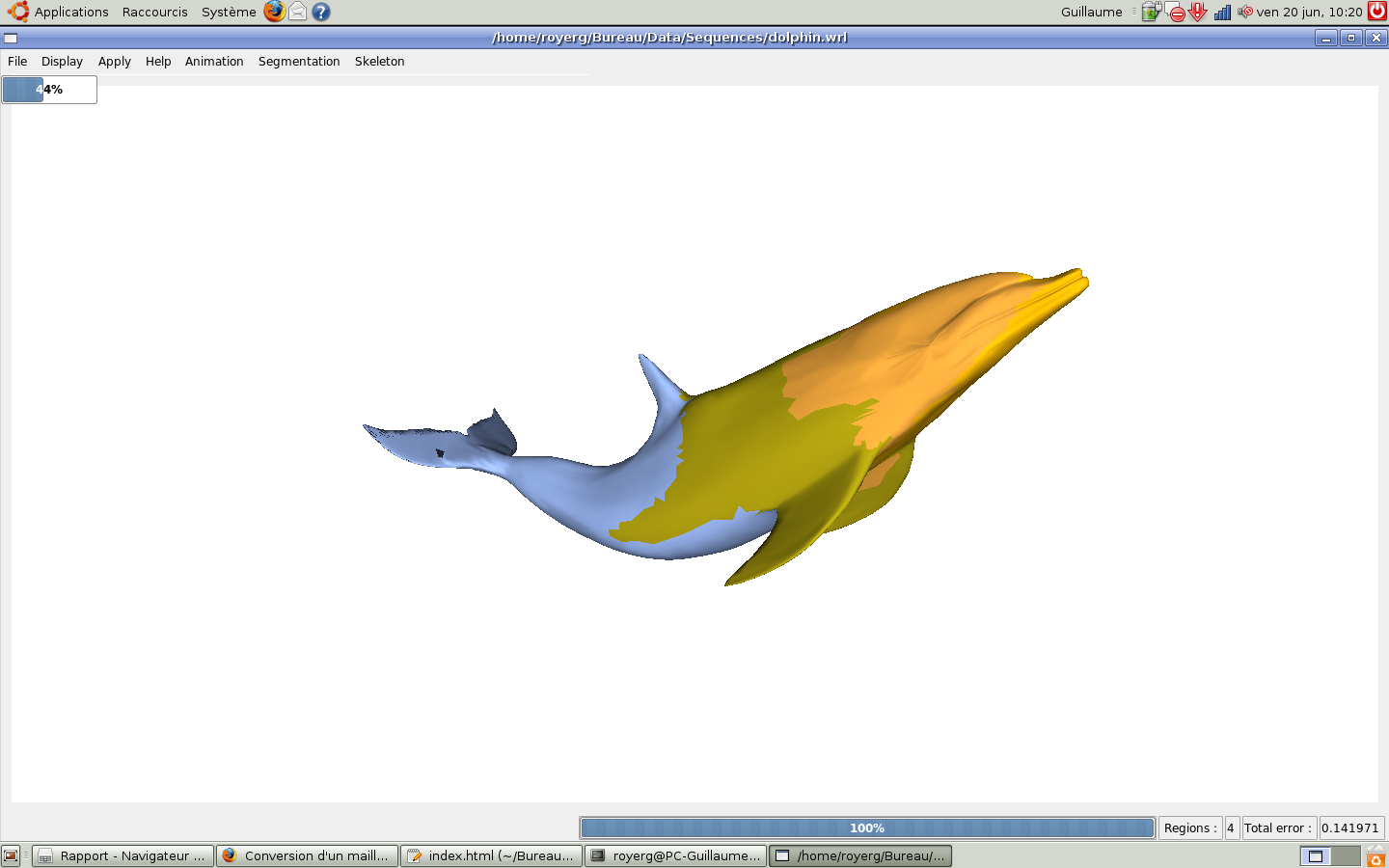
Nous avons pu ensuite observé à l'aide de messages de debuggage que le tableau de booleans stockant l'adjacence des clusters et le tableau des articulations barycentriques semblent corrects. Le reste n'a pas pu être observé à cause de notre problème avec les librairies.
Analyse critique
Problèmes rencontrés
Nos trois principales difficultés ont été les suivantes :
Comprendre l'article et les articles cités
Le problème était que les articles cités étaient nombreux, faisant eux-mêmes référence à d'autres articles. Pour pouvoir commencer à implémenter, il fallait imaginer une structure de données adaptée, et cela aussi a pris du temps, car il fallait pouvoir extraire ces données des fichiers VRML.
Comprendre, faire marcher et modifier l'implémentation de l'algorithme VSA de 2007, ainsi que l'interface, OpenMesh, QT, et QGLViewer pour pouvoir faire marcher le programme final sur ensipsys et nos pc personnels
Cela a occupé plus d'une semaine, du fait de problèmes d'installation à répétition. Les libraires n'étaient pas simples à installer, et comme nous n'avions pas assez d'expérience en Linux cela ne nous a pas facilité la tâche.
Intégrer des librairies extérieures comme NewMat (de Robert Davies), levmar (de Manolis Lourakis) et graph (dans les librairies boost)
C'est le principal problème rencontré en fin de projet. Nous avons dû procéder par tâtonnement, et passer en fin de compte plus de temps à essayer de faire marcher ces librairies extérieures plutôt qu'à implémenter/déboguer l'algorithme. Cela nous a vraiment beaucoup ralentis.
Pistes pour l'amélioration
Rendre le code plus robuste
C'est-à-dire intégrer une gestion des erreurs approfondie, que ce soit pour les inversions de matrices, ou le manque de points dans les clusters (source d'erreurs dynamiques).
Intégrer les librairies extérieures
C'est le principal point bloquant, une grande partie du code, la plus intéressante, n'a pas pu être testée à cause de cela. Les essais/erreurs d'inclusion de librairies étaient vraiment fastidieux.
Tester les différentes variantes dans le code
De nombreux paramètres sont à notre disposition pour améliorer le programme : options d'optimisation dans les librairies extérieures, variantes locales dans le code comme l'utilisation des articulations barycentriques ou les moyennes de matrices.
Tester la valeur de différents paramètres comme K (nombre de clusters)
Et même à long terme rajouter le calcul de K optimal comme suggéré, dans l'algorithme des K-means lui-même.
Bilan du projet
Notre principal regret est de n'avoir pas pu nous concentrer sur les points essentiels de l'algorithme à cause de problèmes extérieurs. Alors que nous abordions la partie centrale du programme, que les résultats les plus intéressants allaient pouvoir être obtenus, nous avons été confrontés à des problèmes sans fin d'intégration de librairies.
Mais les points positifs, au bout de ces 4 semaines, sont nombreux : nous avons appris des points plus fins de C++ (comme le passage de pointeur de fonction en paramètre), nous avons amélioré notre connaissance de Linux, nous avons appris à nous immerger rapidement dans du code inconnu, et enfin nous avons découvert QT et OpenMesh. Nous avons aussi appris à travailler en groupe en autonomie, à gérer les problèmes de toutes sortes en répartissant le travail le plus efficacement possible en gardant un oeil sur les ressources disponibles (temporelles, informatiques, humaines).