Zoé Dubois Dit Laroy, Sarah Kandil, Thibault Serot, Damien Wetterwald
Tuteurs : Cédric Gérot, Franck Hetroy
Sommaire
Introduction
Notre projet s'inscrit dans le Projet Jeunes Chercheurs du GdR ISIS. Son but était de développer des techniques d'analyse multirésolution pour les séquences 3D animées dans le cas de maillages triangulés.
Nous avons divisé notre travail en deux parties.
- Dans un premier temps, nous avons créé l'interface pour travailler sur nos maillage et les afficher et nous avons implémenté les schémas de subdivision spatiale, temporelle et spatio-temporelle couplée pour le cas régulier.
- Ensuite, deux d'entre nous ont géré le cas irrégulier pour les subdivisions, et les deux autres ont travaillé sur l'analyse multirésolution.
Cette page web présente l'ensemble de nos travaux.
1. L'interface
Nous avons repris l'interface déjà existante qui permettait d'afficher les cas statiques (.off) et nous l'avons améliorée afin qu'elle puisse traiter les fichiers dynamiques (.wrl). Cette interface permet aussi de choisir quel type et combien de subdivisions l'on souhaite appliquer à notre fichier. Afin de travailler sur un cas régulier, l'interface nous permet de créer un tore paramétrable que l'on peut animer. L'interface est composée de 2 parties : à gauche se trouve l’affichage des mesh 3D et à droite se trouve l’onglet de configuration.
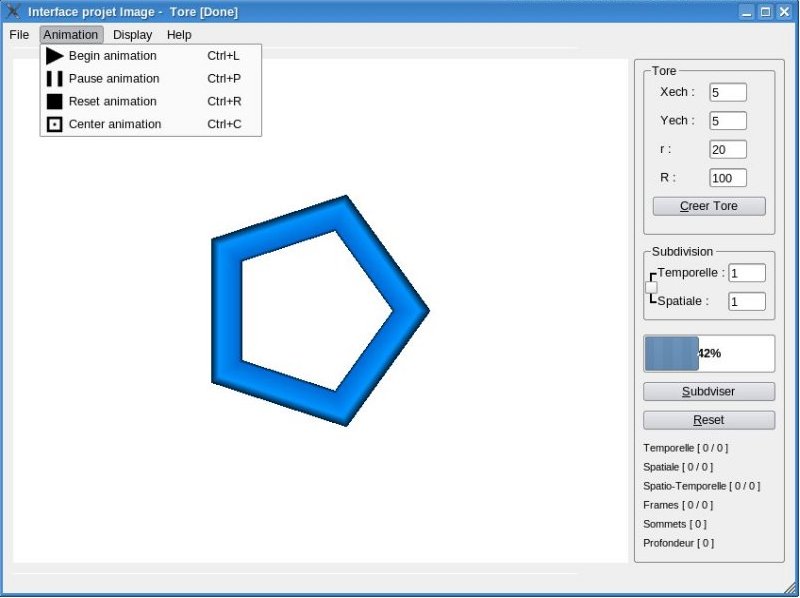
1.1 Onglet de configuration de l'interface
Création d’un tore
- Fonction : permet de créer un Tore
- Paramètres :
- R : Rayon du grand anneau
- r : Rayon de l’anneau
- echX : échantillonnage horizontal
- echY : échantillonnage vertical
La subdivision
- Fonction : Permet de subdiviser un mesh de façon spatiale, temporelle ou spatio-temporelle
- Paramètres :
- Spatial : nombre de subdivisions spatiales
- Temporelle : nombre de subdivisions temporelles
- Case à cocher : couplé ou non
- Principe : lorsque l’on est dans le cas couplé, on va faire min(spatiale, temporelle) subdivisions spatio-temporelles, puis on exécutera les divisions restantes
Les détails d’affichage
- Fonction : Avoir des informations sur le nombre de sommets, de frame, la profondeur de subdivision, le nombre de subdivisions effectuées, la position dans l’animation
- Paramètres :
- Bouton reset : fait un reset de l’environnement
1.2 Les commandes clavier
- 4 : permet de passer à un niveau de subdivision plus grossier
- 6 : permet de passer à un niveau de subdivision plus fin
- + : permet de passer à la frame suivante
- - : permet de passer à la frame précedente
- ctrl + L : lance l’animation
- ctrl + P : met en pause
Schéma de subdivision dans le cas régulier
La séquence d'entrée : construction du tore
Les schémas de subdivision
Définition d'un masque et méthode d'application d'un stencil
Un masque est une matrice dont on peut extraire les stencil pour subdiviser un maillage. Dans le cas d'un maillage composé de quadrilatères, ce masque est une matrice. Dans notre cas, notre maillage est composé de triangles, donc chaque ligne d'une matrice est un peu décalée par rapport à celles du dessus et du dessous.
A partir du masque, pour récupérer les stencils, il faut prendre une valeur sur deux en partant du milieu, puis en partant des valeurs autour du milieu. L'exemple dans le cas spatial devrait bien aider à comprendre le fonctionnement.
Le schéma spatial pur
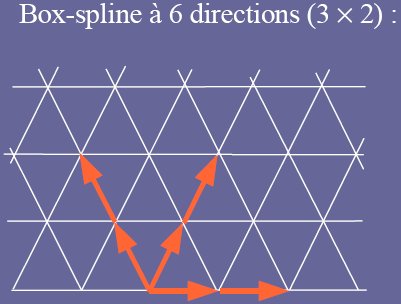
Nous avons utilisé le schéma de Loop pour implémenter la subdivision spatiale. C'est une subdivision avec une box-spline à 6 directions et qui nous garantit une continuité C2.
Construction du masque: Pour construire le masque, il faut regarder la box-spline six directions du schéma de Loop. Chaque direction décrit la manière de translater le masque temporaire pour arriver à la version suivante du masque.
Translation vers la droite
Translation vers la droite
Translation en diagonale vers la droite
Translation en diagonale vers la droite

Translation en diagonale vers la gauche
Translation en diagonale vers la gauche

Finalement, nous obtenons le masque suivant :
Pour implémenter cet algorithme, nous faisons cela en trois étapes :
- Un premier parcours de toutes les faces, afin de calculer les coordonnées des nouveaux sommets à partir des anciens (en utilisant le stencil du bas),
- Un parcours de tous les sommets, afin de calculer leurs nouvelles coordonnées (en utilisant le stencil du haut),
- Un second parcours de toutes les faces, afin de supprimer les anciennes faces et de recréer les nouvelles.
La deuxième étape ne pose pas de problème particulier car, comme cela peut se voir avec le stencil, nous n'avons besoin que des sommets voisins du sommet sur lequel nous sommes en train de travailler. Un simple VertexVertexIterator d'OpenMesh suffit donc.
En revanche, la première étape était un peu plus difficile à implémenter. En effet, nous travaillons sur les faces, et comme le montre le schéma ci-dessous, lorsque nous travaillons sur la face hachurée en vert, nous avons besoin des coordonnées des points pointés par une flèche bleue pour calculer le nouveau point indiqué par la croix.
Or, OpenMesh ne nous permet pas d'avoir accès directement au point qui ne se trouve pas sur la face. Nous avons donc rajouté deux propriétés aux demi-arêtes :
- un booléen DejaPasse, qui nous informe si nous sommes déjà passés sur l'arête (et non la demi-arête),
- un vertexHandle NouveauSommet, qui stocke la coordonnée du point opposé à la demi-arête.
Les résultats de cet algoritme ont été très concluants, et ce pratiquement immédiatement. Voici une image du tore avant subdivision et une image du tore après subdivision :
|
Le schéma temporel pur
Pour le schéma temporel pur, nous avons utilisé une box-spline à 4 directions dans le temps. Elle nous permet d'avoir une continuité C2 de même.
Le masque obtenu est le masque [1 4 6 4 1] que nous appliquons à chaque frame.
L'implémentation de cet algoritme n'a posé aucune réelle difficulté, et les tests ont été passés avec succès rapidement.
Le schéma spatio-temporel découplé
Ce schéma n'est pas le but de notre projet, mais il est intéressant de noter que le schéma spatio-temporel découplé revient en fait à faire une subdivision purement spatiale suivie d'une subdivision purement temporelle. Nous avons obtenus de très bons résultats, justes et rapides, très rapidement puisque ce n'était que la concaténation de deux algorithmes déjà implémentés et testés.
Le schéma spatio-temporel couplé
Ce point était vraiment l'objectif principal de notre projet. Nous devions implémenter le schéma spatio-temporel couplé à une seule direction temporelle, comme ceci :
Cependant, après avoir implémenté ce schéma, nous nous sommes aperçus qu'il ne donnait pas les résultats escomptés. En effet, lors d'une séquence avec un maillage qui ne bouge pas, les anciens points sont influencés par leur voisins dans l'espace alors que les nouveaux points ne le sont pas.
Nous avons donc essayé d'implémenter un schéma spatio-temporel couplé un peu différent, en rajoutant une direction temporelle :
Avec ce schéma, nous avons obtenu le masque suivant :
puis nous en avons déduit les stencils suivants :
| a | la nouvelle coordonnée des sommets existants à la frame t |
| b | la nouvelle coordonnée des nouveaux sommets à la frame t |
| a' | la nouvelle coordonnée des sommets existants à la frame t+1 |
| b' | la nouvelle coordonnée des sommets existants à la frame t+1 |
L'implémentation de l'algorithme a été assez rapide là aussi. Mais cette fois ci, les résultats étaient bons.
Schéma de subdivision dans le cas irrégulier
Le schéma spatio-temporel découplé
Il n'y a rien à faire du point de vue temporel, seul le cas spatial doit être revu afin de traiter les sommets irréguliers, c'est-à-dire dont la valence (v) est différente de 6.
Les stencils de Loop modifiés nous ont été donnés :
L'implémentation de cet algoritme n'a pas été très difficile, compte-tenu de la façon dont nous avions implémenté le cas régulier. Les résultats avec un maillage semi-régulier (cheval de Basile Sauvage) sont très bons.
Le schéma spatio-temporel couplé
Nous avons appliqué la même méthode que dans le cas découplé, ce qui nous donne les stencils suivants :
L'idée était de généraliser la méthode appliquée dans le cas régulier.
Pour cela, on cherche à trouver alpha et beta de manière à ce que le schéma de subdivision soit convergent et continu.
Nous avons utilisé la méthode de calcul des valeurs propres de la matrice de subdivision dans le domaine de Fourier développé dans l'article de recherche de L. Barthe, C. Gerot, M.A. Sabin and L. Kobbelt intitulé "Simple computation of the eigencomponents of a subdivision matrix in the Fourier domain"
Le point fort de cette méthode est que la taille des blocs de la matrice de subdivision ne dépend plus de la valence du sommet irrégulier, on a donc plus qu'un unique calcul à effectuer pour toutes les valences.
Nous avons donc calculé la transformée de Fourier de la matrice de subdivision et plus précisement le bloc pour la fréquence w=0.On obtient une matrice du type suivant.

On a cherché les valeurs propres dans le cas général mais nous n'avions pas une puissance de calcul suffisante pour obtenir un résultat probant.
Nous avons alors remarqué que dans le cas régulier alpha=2*beta, on a donc imposé alpha=2*beta dans le cas général. Cela nous a permis d'obtenir un résultat très interessant: pour beta = 6/v, on obtient exactement les mêmes valeurs propres que dans le cas régulier. Il est à noter que pour v=6, on retombe bien sur les valeurs d'alpha et beta du cas régulier
L'implémentation nous donne de bons résultats, cette méthode semble être valide.
Analyse Multirésolution
Théorie de l'analyse multirésolution
L'analyse multirésolution consiste à étudier la subdivision afin de pouvoir déterminer les valeurs d'un "ancien" point seulement à partir des nouveaux points . Cela permet ainsi d'avoir une méthode de calcul réversible. Les équations pour le cas spatial pur du schéma de Loop nous ont été fournies. Nous avons du les comprendre et les implémenter dans notre interface. Nous avons de même déterminé les équations réversibles dans le cas temporel pur.
Le cas découplé est simple, il faut alterner le spatial pur et le temporel pur. La seule difficulté est de stocker les détails dans le bon ordre, c'est-à-dire ne pas mélanger les détails spatiaux et les détails temporels (en intervertissant, il est possible de chercher des détails qui n'existent pas).
Le but du projet est néanmoins l'implémentation d'une analyse spatio-temporel couplée. Nous avons cherché à déterminer les équations sans néanmoins arriver à des résultats concluants, ni pour le spatio-temporel à six directions, ni pour le spatio-temporel couplé en rajoutant les deux directions temporelles. Dans chacun des cas, les équations étaient plus compliquées et n'aboutissaient pas.
Avec plus de temps, il aurait fallu creuser les schémas, peut-être changer la modélisation, et essayer avec d'autres stencils (notamment un mélange du couplé et du non couplé).
Méthode de calcul pour le schéma
L'image suivant nous montre bien comment le schéma fonctionne dans le cas spatial pur. Les anciens points et les détails (ici nuls dans la subdivion) sont en entrée. En ressort l'ensemble des nouveaux points. On obtient ainsi les équations suivantes pour coder l'analyse :
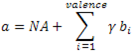
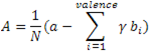
Structure de données
Pour les coordonnées : un tableau de vecteur de coordonnées
Nous avons fait ce choix plutôt qu’un vecteur de vecteur de coordonnées car le nombre de points augmente seulement lors de subdivisions spatiales ou spatio-temporelles et que nous avons jugé plus intéressant de rajouter les nouveaux points après les anciens points.
Les coordonnées se composent des informations (x, y, z) mais aussi du niveau de profondeur du point donné par le champs depth, de son handle donné dans openMesh par le champs v_it (ATTENTION : on ne modifie le handle du point que pour la première frame, il est inintéressant de modifier cette donnée sur toutes les frames)
Pour les faces : un arbre quaternaire
La structure de l’arbre ne force pas un arbre quaternaire, il est possible d’augmenter ou de diminuer le nombre de nœuds.
Il est possible d’afficher l’arbre complet, ou seulement les faces d’un niveau de profondeur donné.
Pour l’ordre de subdivision : un vecteur de booleen
Les subdivisions inverses ne marchant pas sur les subdivisions couplées, nous avons décidé de prendre comme convention qu’une subdivision couplée correspondait à la succession d’une subdivision spatiale puis temporelle.
Les formats de fichiers supportés
- .dat : importe et crée des fichiers multirésolutions statiques
- .wrl : importe et crée des séquences animées
- .off : possibilité de créer des fichiers statiques .off, il est possible d’ouvrir ce type de format aussi, mais on ne peut le subdiviser, pour cela il aurait fallu réécrire la fonction parsant les .off déjà existante dans openMesh. Le but du projet étant de travailler sur des maillages animés, nous n’avons pas jugé utile de refaire le parser.
- .dat + .cro : importe et crée des fichiers multirésolutions animés :
- Le format .dat contient les coordonnées des points à leur niveau de détails le plus fin, ainsi que les informations de construction des faces
- Le format .cro est un format créé par nos soins. Il s’organise ainsi : La première ligne contient l’ordre dans lequel les subdivisions spatiales et temporelles ont été exécutées. Ensuite viennent les coordonnées des points pour chaque frame.
Nous avons choisi ce format plutôt qu’une succession de .dat car les faces restant les même au cours de l’animation, il nous semblait que cela serait une perte de mémoire que de dupliquer cette information.
Exemple: le félin
|
Conclusion
Tout d'abord, ce projet nous a permis de connaitre des librairies connues en image. OpenMesh est une librairie qui est fort utile dans les cas simples mais dès que l'on rentre dans des cas plus complexes, elle est beaucoup moins pratique! Nous avons pu par ailleurs découvrir l'outil OpenGL pour visualiser notre surface
Il nous a aussi permis d'appréhender le travail de chercheur: on peut passer beaucoup de temps sur un problème sans pouvoir malheureusement implémenter quoi que ce soit. On peut aussi tomber sur des résultats auxquels on ne s'attendait pas qui nécessite de revoir la théorie sous un autre angle.
Ce projet a été très formateur car il nous a permis à la fois de découvrir de nouveaux outils mais aussi de mener à bien un projet long (1 mois), ce qui nécessite une bonne organisation surtout lorsque l'on est un groupe de 4 personnes.