Projet Image 2009

Mise en correspondance de deux maillages bruités

par Simon COURTEMANCHE, Antoine KUHN, Xavier MARCHAL et Bertrand RICHARD

Introduction

Tuteurs de projet

Franck Hétroy est maître de conférences à l'Ensimag, titulaire d'un master de mathématiques appliquées (Ensimag et UJF) et d'un doctorat de Grenoble INP. Il est co-responsable de la spécialité "Graphics, Vision and Robotics" du Master of Science in Informatics at Grenoble (MoSIG). Il est en charge, d'un point de vue pédagogique, de l'atelier de réalité virtuelle de Grenoble INP. Il est membre des associations Eurographics et SPECIF. Ses travaux de recherche se font actuellement au sein de l'équipe EVASION de l'INRIA, située à Montbonnot.

Romain Arcila est doctorant 1^ère année, et travaille sur la segmentation de séquences de maillages. Son co-directeur de thèse est Franck Hetroy. Il développe actuellement une librairie/application de segmentation de séquences de maillages. Il a donné des cours d'algorithmique à l'Ensimag en début d'année.

Lieux de travail

Nous avons effectué la première semaine de notre projet dans l'atelier de réalité virtuelle de l'Ensimag, situé à Montbonnot, pour utiliser le scanner 3D dont nous avions besoin. Puis, nous avons travaillé dans la salle E303 de l'Ensimag, car il s'agissait de la seule salle qui disposait des bibliothèques C++ dont nous avions besoin.

Contexte du sujet

L'Ensimag a acquis à l'automne 2007 un scanner 3D de bureau. Ce scanner permet de convertir des modèles 3D réels en maillages virtuels, qui peuvent ensuite être visualisés et manipulés pour des applications très diverses :

effets spéciaux pour le cinéma

prototypage virtuel pour l'industrie (automobile, aéronautique, ...)

restauration virtuelle d'oeuvres d'art

analyse scientifique d'échantillons géologiques

Un premier projet l'an dernier avait pour but de tester ce scanner, ainsi que le logiciel fourni. Il a constaté que le logiciel ne fonctionnait pas aussi bien qu'indiqué en publicité et que les maillages générés avaient de nombreux artefacts. Ainsi, notre sujet proposait d'implémenter un algorithme permettant de mettre en correspondance deux maillages bruités d'un même objet à des positions différentes. Ceci serait très utile pour le scan d'objets 3D, car un scan n'est jamais parfait. En scannant l'objet plusieurs fois à des positions différentes, on pourrait reconstituer l'objet entier.

Outils utiles au projet

Utilisation du scanner

Le scanner 3D dont nous avons disposé a un fonctionnement assez simple, il parcourt un objet à l'aide d'un faisceau laser et crée un maillage de la partie visible de l'objet. Pour avoir l'objet complet, il faut donc faire plusieurs passages, en tournant un peu l'objet à chaque fois, pour cela, l'appareil dispose d'un plateau rotatif automatisé.

Ensuite une fois tous les scans exécutés, il faut assembler les différents maillages ensemble. Il y a une option pour le faire automatiquement mais nous nous sommes vite rendus compte qu'elle n'est pas vraiment au point, l'assemblage ayant échoué sur tous nos essais. Il faut alors placer des pins sur deux des maillages, en essayant de les faire correspondre le plus possible. Une fois les pins placés (au moins trois), on clique sur le bouton align, le programme tente alors, sûrement grâce à l'algorithme ICP de trouver la meilleure correspondance entre ces maillages. Cela marche la plupart du temps, cependant il est déjà arrivé que l'alignement ne marche pas. Nous n'avons pas trouvé de solution dans le programme pour remédier à ce problème.

Placement de 4 pins sur deux maillages d'un objet

Une fois les maillages mis en correspondance, il reste à les fusionner, grâce à l'option fuse. Ici encore ça ne fonctionne pas toujours, cela dépend de l'erreur des correspondances, de plus, les maillages capturés ont très souvent des trous, l'objet final est donc difficilement parfait, cependant cet appareil reste intéressant, bien qu'il faille passer du temps sur les options, et sur les fonctionnalités du programme pour avoir un maillage correct à la fin.

Maillage final d'un playmobil

Utilisation et installation des différents logiciels

QGL Viewer

La librairie QGL Viewer fournie permet de visualiser des données 3D. Elle utilise Qt. Cette librairie était déjà installée sur les machines que nous avons utilisées. Cependant, selon les machines, cette librairie se nomme soit libQGLViewer, soit libqglviewer, ce qui nous a posé quelques soucis pour l'inclusion de cette librairie à la compilation.

Open Mesh

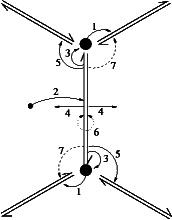
OpenMesh est la librairie que l'on a utilisée pour gérer les maillages dans tout le projet. Elle fonctionne sur une structure de maillage appelée "demi-ailée". Le principe est assez simple, les sommets du maillage sont reliés par des demi-arêtes orientées. Ainsi une face, triangulaire par exemple, sera composée de trois sommets et trois demi-arêtes, qui définiront un circuit. Le sens de parcours des arêtes permet de définir une normale à la face, et si une autre face est adjacente à la première, l'arête qu'elles auront en commun sera composée de deux demi-arêtes, de sens opposés. Cette structure permet de stocker facilement un grand nombre d'informations sur le maillage et est très utilisée.

Schéma de la structure demi-ailée (ou halfedge)

Cette librarie dispose d'un bon nombre de méthodes et d'opérations prédéfinies sur les maillages et est globalement assez simple à comprendre, la documentation est par contre assez mal organisée et il est parfois difficile de trouver ce que l'on cherche. Elle est disponible à cette adresse.

Pour notre projet, nous avons utilisé les Trimesh, qui sont des meshs à face exclusivement triangulaires. l'accès simple aux sommets et aux voisins des sommets nous a particulièrement bien servi pendant le projet.

Conversion QT3/QT4

Qt permet de créer des interfaces graphiques. Les versions récentes des packages Qt4 comportent des extensions pour supporter les programmes écrits en Qt3 (comme l'interface qui nous avait été fournie par exemple). Nous avons néanmoins rencontré quelques soucis avec des versions apparemment anciennes du package Qt4. Ceux-ci nous ont poussés à convertir le code en qt4, d'une part avec le logiciel qt3to4, et d'autre part manuellement. (qt3to4 ne fait pas tout.) L'ensemble de ces modifications sont regroupées dans le fichier README du package que nous avons implémenté.

Ubuntu 9.04 et carte graphique Intel

En essayant de faire tourner notre interface sur la distribution 9.04 d'Ubuntu, nous avons rencontré le message d'erreur suivant :

"freeglut (./mytest): Unable to create direct context rendering for window 'MyTest'
This may hurt performance."

Notre programme s'est lancé correctement, mais l'affichage était complètement saccadé. Apparemment, ceci venait d'un bug au niveau du driver de carte graphique Intel. Ce bug est répertorié dans les notes de réalisations d'Ubuntu 9.04.

Cas d'une transformation rigide: Iterative Closest Points (Horn, 1987)

On dit d'une transformation qu'elle est rigide si elle peut se décomposer en une rotation et une translation. L'algorithme ICP permet la mise en correspondance de maillage rigide en utilisant ces transformations. Nous avons implémenté l'algorithme ICP comme décrit dans le papier de recherche [BK92]

Les grandes étapes de cet algorithme itératif sont les suivantes:

La première étape consiste à calculer pour chaque sommet de la source un correspondant dans le maillage cible. Cette étape est effectuée en prenant le point le plus proche avec la distance euclidienne (Closest Point step). L'étape suivante consiste à calculer la transformation à partir des deux ensembles de points calculés. Ici une méthode utilisant les quaternions et un travail de calcul matriciel (essentiellement construction d'une matrice symétrique à partir de centre des masses des maillages source et cible permettant de trouver la rotation et la translation). La deuxieme étape applique la transformation sur le maillage source et la dernière calcule l'erreur quadratique entre le maillage source transformé et la cible. L'algorithme recommence ensuite la première étape en prenant en considération le nouveau maillage transformé. L'algorithme se termine lorsque l'on a dépassé un nombre d'itérations défini par l'utilisateur ou lorsque l'erreur calculée entre deux étapes successives est inferieure à un seuil fixé.

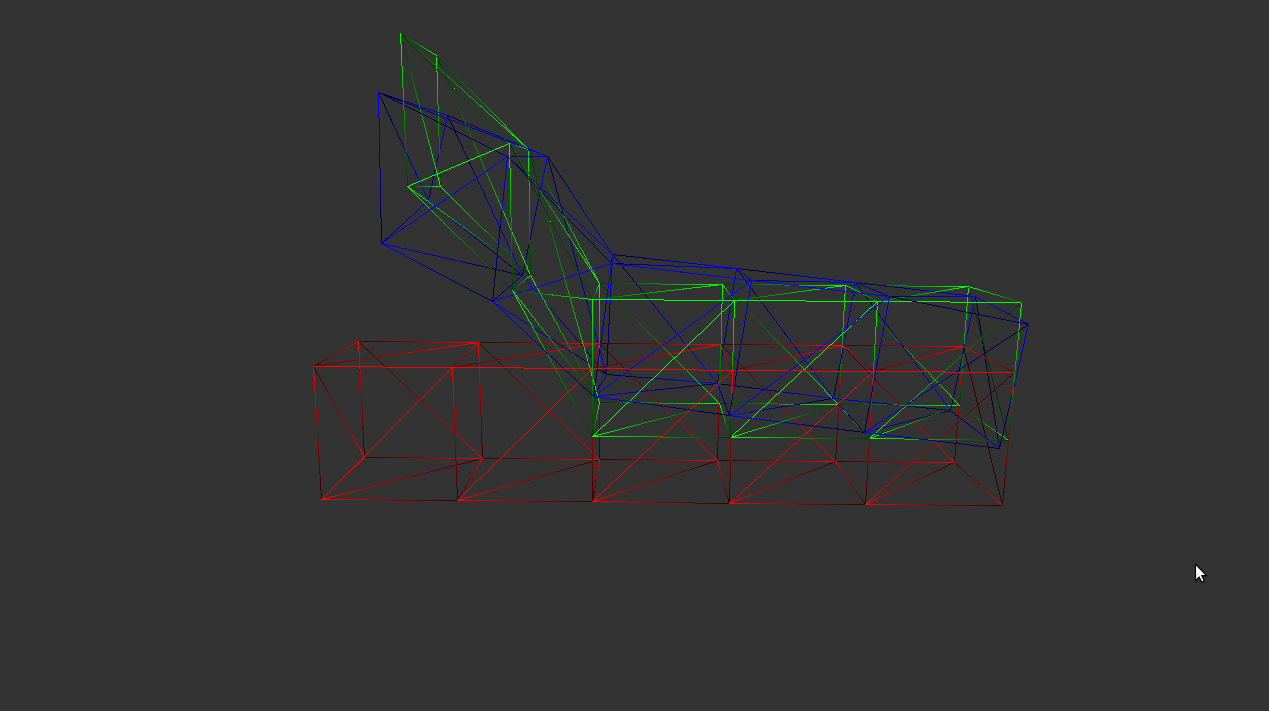
Cet algorithme a été testé sur différents maillages. Le premier maillage est un triangle auquel on fait subir une rotation. La transformation est calculée immédiatement en une itération par le programme. Nous en donnons le resultat graphique obtenu avec notre interface :

On affiche en rouge le maillage source et la cible en vert. Les correspondances sont données par les lignes bleues. Le resultat est confondu avec le maillage cible et n'est pas visible.

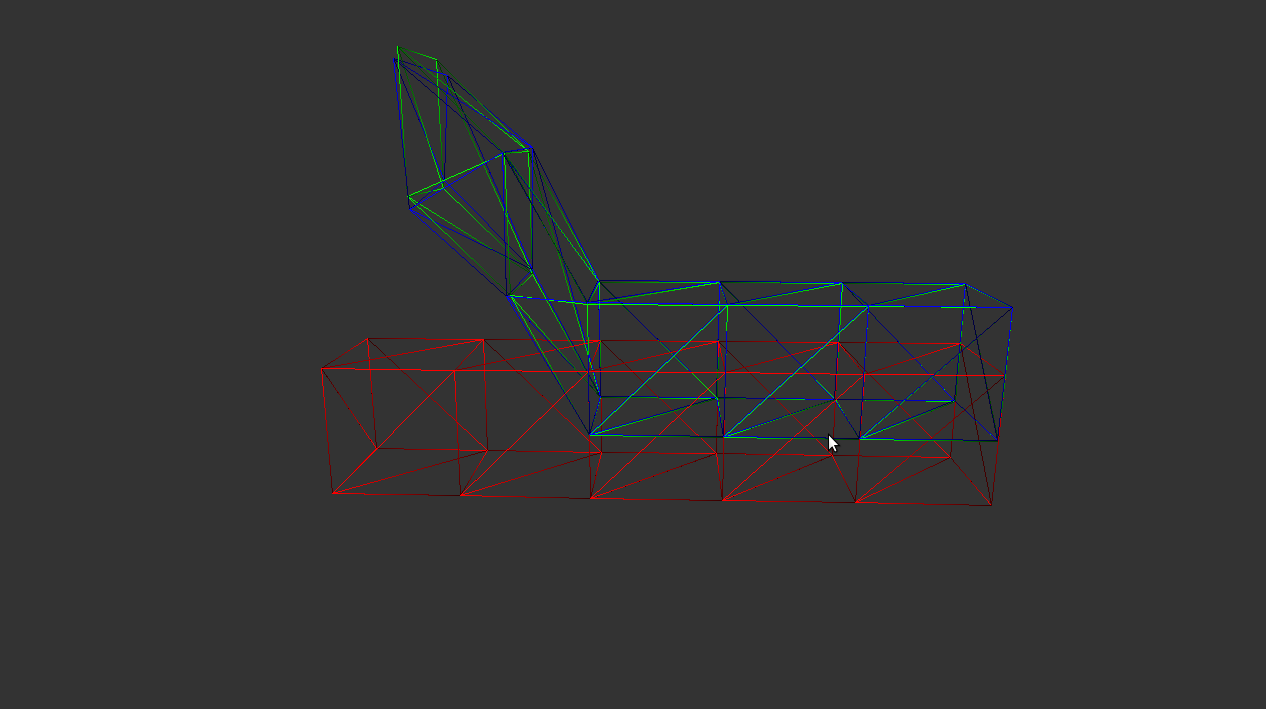
Un autre exemple montre le résultat obtenu sur un maillage légérement deformé de 2900 sommets et de 5500 faces. On effectue quinze itérations de l'algorithme ICP et on stocke les différents maillages obtenus à chaque étape dans des fichiers .OFF. On visionne ensuite le résultat avec le logiciel Meshlab en affichant un résultat intermédiaire :

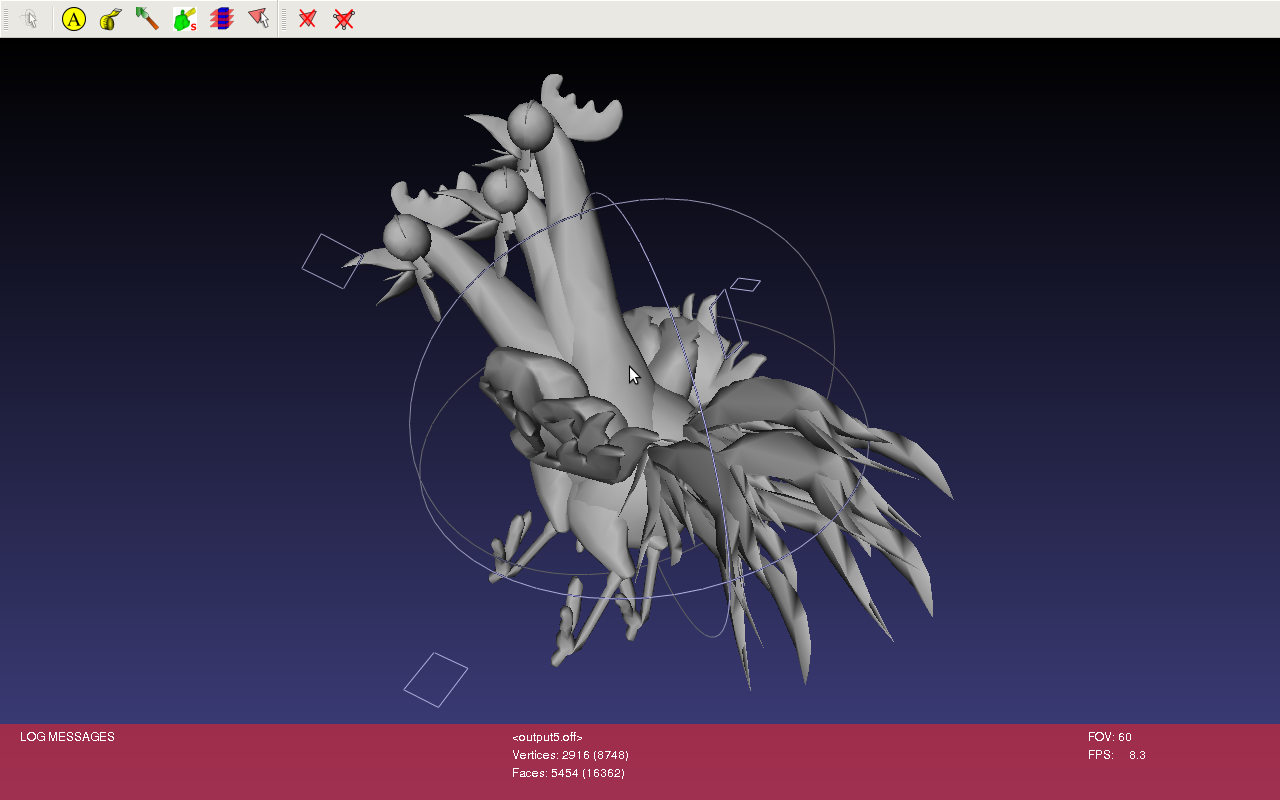
L'algorithme ICP est efficace pour la mise en correspondance de maillages rigides. Son implémentation nous a permis de nous familiariser avec la librairie OpenMesh.

Description et implémentation des différentes étapes de l'algorithme pour traiter le cas des transformations non rigides

Description globale

Comme précisé précédemment, ICP ne peut être efficace dans le cas où la transformation entre les deux maillages n'est pas rigide. Il existe actuellement de nombreuses recherches pour traiter le cas d'une transformation non rigide. Ainsi, une équipe de Stanford university a proposé une méthode l'an dernier [HAWG08] pour résoudre ce problème. Nous devions implémenter cette méthode.

Celle-ci est composée de 3 étapes majeures :

Un prétraitement ("Preprocessing", implémenté par Antoine) des maillages pour calculer leurs différentes propriétés nécessaires à l'algorithme.

Un calcul des correspondances ("Correspondence computation", implémenté par Bertrand) les plus cohérentes entre les points du maillage source et ceux du maillage cible.

Une déformation du maillage source pour qu'il ressemble de manière précise au maillage cible. Cette étape se décompose en deux parties :

• Une recherche des parties du maillage qui pourraient être approchées par une transformation rigide ("Clustering", implémentée par Xavier)
• Une recherche des déformations les plus adaptées pour chaque partie en utilisant une minimisation d'énergie (voir la partie "Energy Minimization", implémentée par Simon)

On donne ci-dessous le schéma global de l'algorithme :

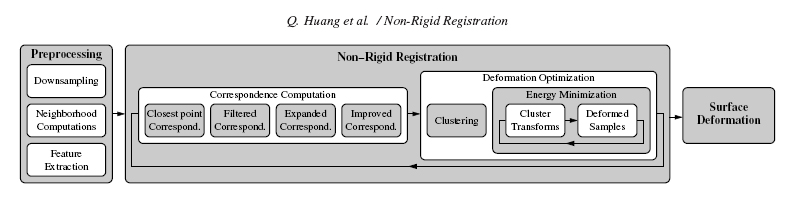
Preprocessing

Cette partie comporte trois tâches principales :

"DownSampling"

"Neighborhood Computation"

"Feature Extraction"

DownSampling

Cette partie consiste à simplifier le maillage. En effet, l'algorithme que l'on applique ensuite est assez coûteux, et l'on peut avoir des maillages de plusieurs centaines de milliers de points, on veut donc toujours se ramener à un maillage d'au plus quelques milliers de points (moins de 3000 généralement). Nous avons rencontré des problèmes importants sur cette partie, dûs au techniques employées par les auteurs de l'article.

Premièrement, on utilise un échantillonnage uniforme de l'espace. En partitionnant l'espace de manière uniforme, on prend pour chaque cube de l'espace, un point du maillage, celui qui est le plus proche du centre du cube. Ensuite, on ajoute des points, avec la méthode explicitée dans le papier [RL01]. Elle consiste en la projection des normales de la surface sur une sphère, puis à l'échantillonnage uniforme de cette sphère. C'est à dire que l'on prend des points afin d'avoir une répartition uniforme des normales.

Pour la première partie, nous avons utilisé une grille, afin de partitionner l'espace. Ensuite pour chaque point de la grille nous avons cherché le point le plus proche, et l'avons copié dans un autre maillage. Ici se posent deux problèmes. Le premier, est que cette méthode prend un peu de temps, environ 50 secondes pour un mesh de quelques milliers de points. Le deuxième, bien plus important, est qu'elle ne garde que les points, nous n'avons ensuite plus aucune information sur les arêtes, sur la connexité entre les sommets, alors que celle-ci doit être utilisée dans la suite. Pour pallier à ces problèmes, deux solutions ont été trouvées. La première consiste en l'utilisation de la structure de donnée "Octree" pour la partition de l'espace. Cette méthode permettrait de gagner du temps à l'execution. Cependant pour des raisons de temps, elle n'a pas été implémentée. La deuxième consiste en l'application successive de la fusion de deux points. Cela permet de garder les arêtes au fur et à mesure de l'execution. De la même façon, nous ne l'avons pas implémenté faute de temps.

La deuxième méthode étant bien plus complexe, le papier de recherche s'appuyant sur un autre, et comme l'on avait déjà des problèmes avec le downsample uniforme, nous avons décidé d'abandonner cette partie, et d'utiliser directement des meshs de quelques milliers de sommets.

Neighborhood Computation

Pour cette partie, le but est de pré-calculer, et de stocker, les 15 plus proches voisins de chaque point du maillage, par rapport à la distance géodésique. La distance géodésique entre deux points est la distance entre ces points en ne passant que sur la surface du maillage. Ici elle est approximée par la distance minimale entre deux sommets en ne passant que par les arêtes du maillage.

La distance géodésique minimale entre deux points est réutilisée ensuite, nous avons donc décidé de la pré-calculer également et de la stocker dans un tableau. Nous avons pour cela utilisé l'algorithme de Floyd Warshall et stocké le résultat dans un tableau n x n ou n est le nombre de sommets du maillage. Cette méthode est en O(n³) ce qui peut prendre très longtemps pour des maillages avec beaucoup de sommets. Ici, avec l'option de compilation -O2, cette opération prend une minute pour deux mille sommets.

Comme une fois qu'on a le tableau, Tab[i][j] est la distance entre les points i et j, on n'a plus qu'à rechercher les 15 plus petites valeurs pour chaque ligne i et on a les indices des quinze plus proches voisins du point i. On stocke ces valeurs sous la forme d'un autre tableau, qui donne pour chaque ligne i les quinze plus proches voisins du point i.

Feature Extraction

Dans les autres parties, on utilise une fonction f d'un point, afin de comparer la forme du mesh aux alentours du point. Cette fonction, appelée Feature Vector, renvoie un vecteur composé des courbures principales estimées au point considéré. On pré-calcule ces valeurs lors de l'étape de préprocessing pour plus de rapidité ensuite. On a un vecteur à plusieurs niveaux, c'est-à-dire que l'on prend plusieurs ensembles de voisins pour estimer les courbures principales, de tailles différentes.

Comme assez souvent dans l'article, la méthode utilisée pour calculer les courbures principales est assez floue et se repose sur un autre papier. Nous avons pour notre part utilisé la méthode du papier [Curvatures estimation on triangular mesh], qui est assez simple à comprendre et bien expliquée. On calcule les courbures principales à différentes échelles, en prenant plus ou moins de points autours du point considéré. Cela nous amène à un resultat sous la forme d'un vecteur de huit valeurs, quatre paires de deux courbures. Cette partie a été réalisée assez facilement une fois la méthode pour l'estimation des courbures trouvée.

Correspondence computation

La mise en correspondance entre le maillage source et le maillage cible comporte 4 étapes principales:

Initial Correspondence Computation

Correspondence Prunning

Correspondence Propagation

Correspondence Fine-Tunning

La première étape consiste à calculer les correspondances initiales avec la méthode 'Closest Points' utilisée dans l'algorithme ICP. On applique la méthode en travaillant sur les subdivisions des maillages source et cible. Dans notre algorithme nous travaillons directement sur les maillages source et cible car la phase de subdivision nécessite un temps de calcul trop long. L'exemple suivant affiche les correspondances calculées avec cette méthode entre la source couleur argent et la cible couleur or :

Les correspondances sont ensuites ameliorées en deux étapes : Premièrement, pour chaque sommet de la source on cherche parmi les voisins de son correspondant dans le maillage cible le sommet qui a la courbure la plus proche du sommet source. On utilise principalement les ensembles de voisins calculés dans l'étape de Preprocessing (Neighborhood Computation) et les courbures principales autour du point (Feature Extraction).

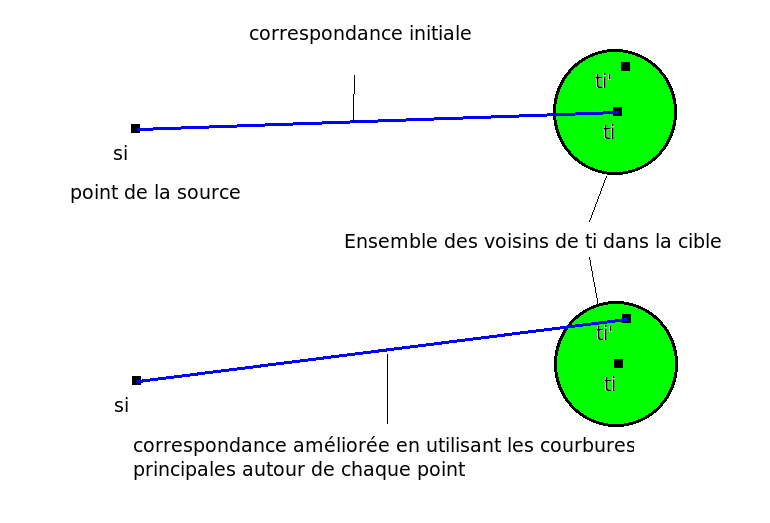
On effectue une deuxième étape dans le sens inverse : pour chaque sommet de la cible mis en correspondance, on modifie le sommet de la source de la même manière en regardant parmi ses voisins. L'exemple suivant montre le résultat obtenu à partir des correspondances de l'image précédente :

La deuxieme étape est l'étape de Correspondence Prunning. Il s'agit ici d'enlever parmi les correspondances calculées celles qui ne sont pas consistantes par rapport aux autres. On dit que deux correspondances (s_i,t_i) et (s_j,t_j) sont consistantes si le rapport d(s_i,s_j)/d(t_i,t_j) est proche de 1 (d est ici la distance géodésique entre deux points du même maillage).

On utilise une méthode provenant du papier de recherche suivant : [LH05]

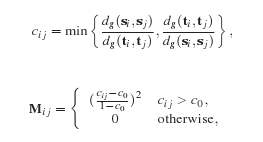
On calcule la matrice symétrique M en la remplissant avec les coefficients c_ij. Les coefficients dépendent du seuil c0 qui détermine l'erreur que l'on accorde dans la consistence des correspondances. On calcule ensuite le vecteur propre principal de la matrice M. Un algorithme itératif à partir des valeurs de ce vecteur permet de remplir un noyau de correspondances.

L'exemple suivant montre le noyau de correspondences obtenu:

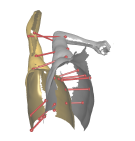
La méthode suivante permet de propager les éléments du noyau de correspondances dans tout le maillage. A la fin de cette étape, tout point du maillage source a un correspondant dans le maillage cible.

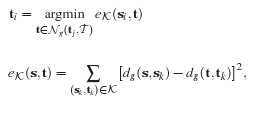
Pour chaque point s_i n'ayant pas de correspondant, on calcule son plus proche voisin s_j qui possède une correspondance (s_j,t_j). On choisit ensuite un correspondant à s_i en prenant un point t parmi l'ensemble des voisins de t_j dans le maillage cible. Ce choix est effectué en calculant l'élément qui a la plus petite erreur de consistence comme décrit sur le schéma ci-dessus. On obtient le résultat suivant:

Nous avons testé l'algorithme de calcul des correspondances sur un rectangle subissant une déformation. Les différentes étapes conduisent au résultat suivant:

Closest Points	Prunning
Propagation

Nous avons ensuite testé cet algorithme sur un maillage de plus de 2000 points. Nous obtenons les correspondances finales suivantes:

Clustering (deformation optimisation)

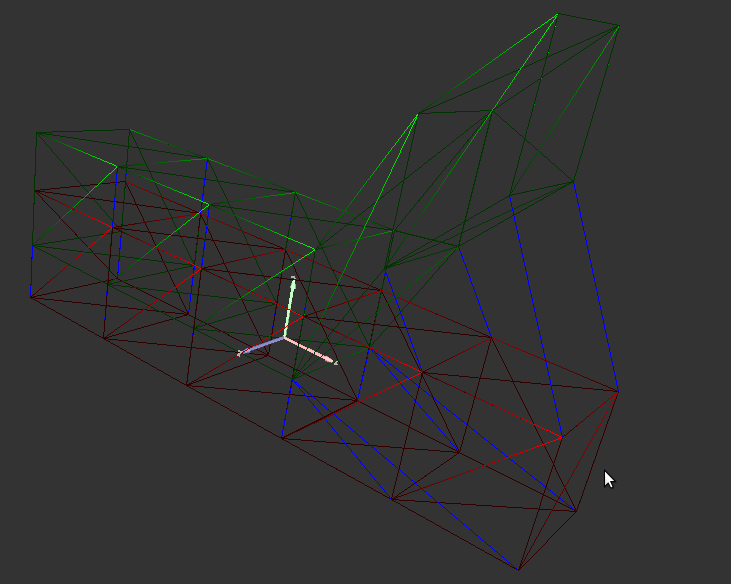
Cette étape consiste à trouver des ensembles de points (appelés des clusters) du maillage qui ont à peu près la même transformation rigide. En effet, nous avons vu que la méthode ICP permettait d'approcher de manière efficace la transformation entre deux maillages proches dans ce cas. La recherche de clusters est décrite dans la partie 5-1 du papier publié par l'équipe de Standford [HAWG08].

Au départ, nous considérons que chaque point du maillage source représente un cluster, auquel est associé une transformation rigide (le cluster associé sur la cible est celui dont le point est la correspondance du point du cluster source). Pour avoir une transformation qui traduit au mieux la forme du maillage au point source, on recherche une transformation sur le cluster dit étendu, constitué du cluster traité et de l'ensemble des voisins des points du cluster. Cette transformation n'est donc pas exacte, car les points d'un cluster n'ont pas tous un par un la même transformation rigide, même si elle est proche a priori. Ainsi, on associe à un cluster l'erreur faite lors de sa transformation. De ce fait, lors de l'implémentation informatique, nous avons défini une structure "Cluster" qui possède notamment comme attributs la liste de ses points, sa transformation associée, et son erreur.

Structure des clusters

struct _Cluster{ //nom du cluster (un numéro) int name; //proprietes de chaque point du cluster list V_set; //points du cluster list pts_source; //points de la cible associés list pts_cible; //liste des clusters voisins list clust_voisins; };

// Rotation et Translation optimum double ** transfo; //erreur associée double erreur; //couleur associée au cluster (pout l'affichage) int ind_color; //entier qui dit si on a déja essayé de fusionner le cluster avec ses voisins int traiter;

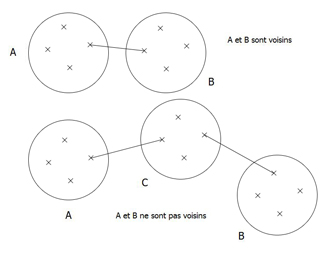
Une fois l'initialisation effectuée, on va chercher à fusionner les clusters entre eux s'ils sont proches et possèdent des transformations proches. Pour cela, on doit définir une relation de voisinage entre les clusters. La publication de l'équipe de Standford nous explique que deux clusters sont voisins si leurs clusters étendus intersectent. Cependant, il nous a semblé que cette définition pouvait poser des problèmes au moment de la fusion car il pourrait exister deux clusters voisins qui n'ont pas d'arètes en commun. Ainsi, on pourrait être amenés à définir un cluster comme la réunion de deux parties du maillage, ce qui nous a semblé, après discussion avec Romain Arcila, flou.
Nous avons donc décider de modifier pour notre algorithme la définition de cluster "voisin": Dans notre étude, deux clusters seront voisins s'ils sont reliés par une arète.

Ainsi, pour chaque cluster non traité appelé C_k, on regarde ses clusters voisins. On applique la tranformation de C_k à ceux-ci et on regarde l'erreur effectué. Si cette erreur est inférieure à un seuil donné, on fusionne les deux clusters. On effectue ceci pour tous les clusters du maillage, autant que l'on peut fusionner des clusters.
Le papier de l'équipe de Standford ne précisait pas la valeur du seuil de fusion à définir. Romain Arcila a envoyé un email à cette équipe qui nous a répondu que cette valeur "valait en général 1/20ième de la densité d'échantillonage"... Cette phrase nous semblant assez mystérieuse, nous avons décidé de fixer l'erreur E_max à la main pour le moment, défini en fonction du maillage traité.

Ainsi, notre algorithme garantit que chaque cluster possède des transformations rigides associées inférieures au seuil fixé, sauf les clusters d'un point qui possèderait des erreurs supérieures au seuil dès le départ. Cependant, il semble judicieux de penser que quelques points isolés ne faussent pas le principe de l'algorithme.

On donne ci dessous quelques screenshots des résultats obtenus pour cette partie. Chaque cluster est représenté par une couleur.

Seuil Emax fixé à 0.8 les clusters des jambes sont appropriés	Seuil Emax fixé à 0.8 Ventre du pinguin
Seuil d'erreur fixé à 3 Le mouvement de la jambe n'est plus pris en compte.	Seuil d'erreur à 0.01 : les clusters des jambes sont très corrects malgré une erreur basse.

Energy minimization (deformation optimisation)

Le but de cette partie est de trouver la déformation du maillage initial qui minimise une énergie E.
Cette énergie est définie comme la somme d'une énergie de correspondance E_corr et d'une énergie de rigidité E_rigid.

Les paramètres λ_corr et λ_rigid sont fixés par l'utilisateur. Nous avons pris λ_corr = 2 et λ_rigid = 1.

Soit S' le maillage recherché, qui approxime le maillage cible en minimisant E. Soit s'_i un sommet de S'. Soit t_i le sommet du maillage cible en correspondance avec s'_i. L'énergie de correspondance E_corr regroupe les sommes des distances de s'_i à t_i, et de s'_i au plan tangent au maillage cible en t_i.

n_i est la normale au maillage cible en t_i. w_i sont des poids calculés à l'étape de propagation des correspondances. α et β sont des constantes. Nous avons pris α = 0.6 et β = 0.4.

Soit S le maillage courant que l'on désire déformer pour approximer le maillage cible. Soient C_k les clusters obtenus à l'étape de clusterisation, C^~_k les clusters étendus correspondants et (R_k,T_k) la transformation correspondante pour approximer le maillage cible, comme défini précédemment. L'énergie de rigidité E_rigid correspond à la distance entre les C^~_k dans le maillage recherché, et le résultat de l'application des transformations (R_k,T_k) aux C^tilde_k dans S.

La minimisation se fait en deux temps. D'abord nous calculons les tranformations (R_k,T_k) comme décrit dans la partie précédente. Ensuite nous minimisons E par rapport à chaque s'_i. La solution correspond à l'annulation du gradient de E selon le vecteur s'_i. Comme E est de degré 2 en s'_i, grad E est de degré 1 en s'_i. Nous obtenons donc un système du type A.s'_i = b, que nous résolvons avec la fonction gsl_linalg_HH_solve de la library [gsl].

En changeant S' en S, nous pouvons itérer. Nous effectuons ainsi 10 itérations.

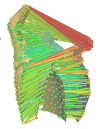
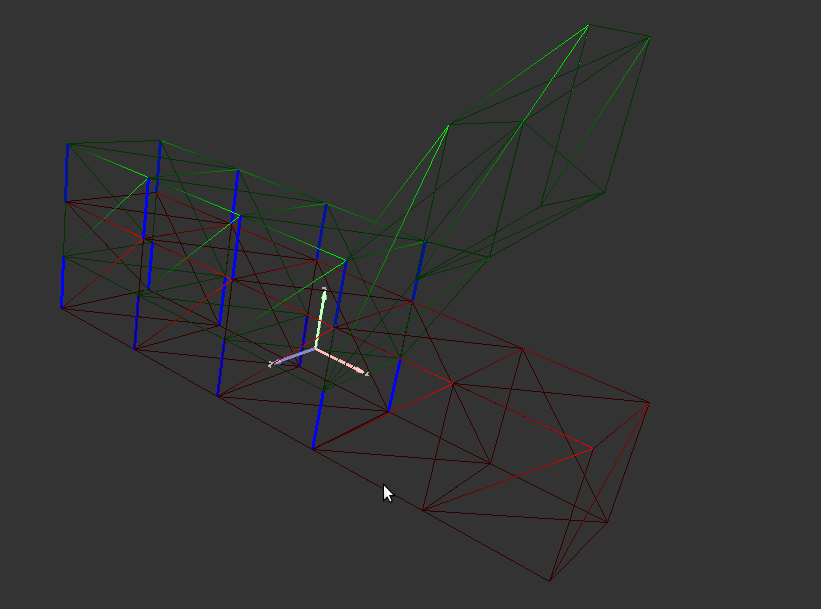
Avec un maillage de 24 sommets et de correspondances idéales, nous obtenons les resultats suivants:

En rouge : le maillage initial.

En vert : le maillage cible.

En bleu : le maillage modifié.

Itération 1	Itération 5
Itération 10	Itération 50 (pour voir)

Assemblage

Une fois l'implémentation des quatre parties terminée, nous avons pu construire un programme qui effectuait la mise en correspondance dans le cas non rigide. Nous devons ci-dessous l'algorithme du programme principal. Nous avons suivi les informations données par l'équipe de Standorf university pour l'implémenter. L'équipe précisait notamment que la mise en correspondance s'effectuait grâce à une boucle itérative, où on alternait un calcul des correspondances et une déformation du maillage. De plus, pour respecter au mieux les informations de l'équipe, le clustering n'est effectué qu'au bout de la dixième itération.

Par manque de temps, nous n'avons pas pu effectuer la boucle finale sur la déformation. Tous nos résultats ont été trouvés avec une seule itération.

Algorithme principal

Compute_Preprocessing(); while(erreur< threshold && iteration< N{    Correspondence_Computation();    init_clusters();    process_clustering();    Init_E();    Minimise_E();    iteration++; }

Interface utilisateur

Nous avons implémenté une interface pour visualiser nos résultats. L'interface permet d'afficher simplement un maillage contenu dans un fichiers .OFF et d'afficher les normales en mode plein ou lignes. L'interface permet ensuite de lancer différentes étapes de notre algorithme à partir d'un maillage source et cible en entrée. On peut calculer les correspondances, les clusters et changer certains paramètres importants.

Nous pensons que cette interface pourrait servir à d'autres groupes lors des prochaines pour commencer leurs projets, car celle-ci permet de visualiser facilement des maillages, des normales, des clusters... Franck Hétroy possède les sources de notre interface. Faites attention si vous voulez la faire fonctionner à bien respecter les instructions conseillées lors de l'installation de QGLViewer ou Open Mesh. Vous devrez modifier votre Makefile afin d'inclure les bon chemins vers les librairies.

sources de l'interface.

Conclusion

Bilan scientifique

Durant tout le projet, il nous a fallu réfléchir sur les explications floues du papier de l'équipe de Standford. En effet, chacun de nous s'est posé de nombreuses questions sur les valeurs des paramètres "magiques" que l'équipe prenait pour obtenir de bons résultats, ou sur leur manière d'implémenter le sujet, car les chiffres donnés concernant la vitesse d'éxecution sont largement inférieurs aux nôtres. Nous expliquons donc les différentes bilans auxquelles nous sommes arrivés sur les différentes parties du sujet :

La partie Preprocessing s'est révélée assez difficile finalement, principalement à cause du manque d'informations et de précision du papier de recherche. Nous avons pu contourner les problèmes pour la plupart des fonctions, sauf pour le downsampling, faute de temps.

La partie de calculs des correspondances semble être la partie la plus facile à implementer par rapport aux autres. Seule la partie de prunning correspondences nécessite de la recherche documentaire. Cette partie est essentielle dans cet algorithme. Le prunning nécessite un calcul de vecteur principal qui peut être optimisé dans notre implémentation en utilisant des librairies traitant ce cas particulier comme la fonction "eigs" de la librairie Matlab qui a été proposée dans le sujet.

Lors de la partie Clustering, l'équipe "oublie" de préciser comment choisir la valeur du seuil d'erreur pour la fusion des clusters. Nous n'avons pas trouvé de manière d'automatiser le choix de cette valeur. Nous le choississons à la main pour chaque maillage

D'un point de vue théorique comme d'un point de vue pratique, la minimisation d'énergie s'applique très bien à des maillages ayant des correspondances idéales. Les résultats obtenus sont visuellement très satisfaisants. Cependant, son application à des maillages ayant des correspondances approximatives produit des résultats totalement incohérents au niveau visuel.

Perspectives

Nous pouvons encore et toujours améliorer les performances de notre programme. En effet, le langage C++ utilise de nombreuses structures optimisées comme les vecteurs, les listes... Nous avons globalement utilisé ces structures, mais il reste encore quelques parties où nous pourrions les utiliser. Cependant, nous avons énormément utilisé des pointeurs en entrée de nos fonctions, afin de ne pas surcharger la pile lors de recopies de variables, nous avons toujours passé l'adresse.

En plus de l'aspect strictement programmation, nous pouvons encore améliorer l'algorithme proposé. En effet, les résultats trouvés sont corrects, mais on peut légitimement penser que nous pouvons encore les affiner. Par exemple, lors de l'étape de recherche des clusters, nous voyons à l'oeil nu que des clusters pourraient être fusionnés, mais l'algorithme ne le fait pas par son implémentation. La valeur de E_max est mystérieuse, on pourrait essayer de rechercher la valeur adéquate de ce paramètre. De même pour le prétraitement où nous pourrions essayer d'effectuer un sous échantillonage efficace, ce qui n'est pas le cas actuellement.

Cependant, nous retiendrons que ce genre de sujet est un axe de recherche actuel, donc que de nombreuses pistes d'améliorations vont sûrement être trouvées lors des prochaines années. Notre algorithme fait appel à de nombreuses méthodes, et si une méthode est améliorée, nos résultats seront plus précis. Ainsi, notre algorithme possède de nombreuses perspectives d'améliorations.

Bilan personnel

Notre groupe est composé de quatre étudiants qui choisiront a priori la filière IRV (nouvellement appelée MMIS) l'an prochain. Nous voulions donc choisir un sujet porté sur l'image. Notre bilan ne peut être que positif. Nous avons pris beaucoup de plaisir à voir des résultats visuels, et il est toujours plus agréable de travailler en riant des résultats obtenues (souvent amusants lorsque les correspondances trouvées étaient complètement fausses!). Le sujet était relativement dur pour plusieurs raisons :

Le sujet comportait de nombreuses coquilles, difficiles à résoudre.

L'implémentation nécessitait un niveau en informatique assez bon. Sur ce point, nous pensons nous être amélioré grandement.

Le sujet était long.

Il a fallu donc être assez rigoureux pour pouvoir finir l'implémentation à quatre. Le travail de groupe s'est bien passé, même s'il est difficile de programmer tous de la même façon, afin d'uniformiser le code global. Ce projet nous a permis, une fois de plus, d'apprendre à travailler en groupe, et à prendre des décisions d'implémentation ensemble, car les fonctions dépendent les unes des autres.

Enfin, le groupe a pu apprécier la bonne disponibilité des tuteurs de stages, qui étaient assez souvent là, et répondaient vite aux questions posées par mail. Merci Franck! Merci Romain !