Introduction
Le principe général du projet est d'adapter et d'implémenter une méthode de reconstruction d'une séquence de maillages à partir d'un flux de points. Les données sont obtenues en filmant un objet en mouvement à l'aide de deux caméras dont la position est fixée. En recoupant les deux images obtenues à un temps t, on extrapole un nuage de points dans l'espace qui servira de support à l'application de la méthode implémentée. Le but est d'obtenir, au final, une reconstitution du mouvement de l'objet sous la forme d'une séquence de maillages temporellement cohérents.
Pour celà, nous nous sommes basés sur une technique récente, décrite dans l'article "Space-time Surface Reconstruction Using Incompressible Flow". Elle s'appuie sur une modélisation de l'objet sous la forme d'un fluide incompressible, dont la masse doit être conservée dans le temps.
Les images sont présentées sous forme de screenshot de notre logiciel AnimViewer, concu en java+java3D spécialement pour ce projet. Sur les images, le rouge désigne l'intérieur des objets, et les petits cubes bleus, leur surface.
Pour l'implémentation, nous avons utilisé la librairie CGAL.
Principe général de la méthode
La méthode s'effectue en trois étapes principales :
Réduction du problème à un ensemble d'éléments finis
Nous avons créé, pour simplifier notre implémentation, et surtout réduire l'espace mémoire nécessaire au stockage de notre maillage, d'utiliser un maillage implicite, c'est-à-dire un maillage "hyper-cubique" (ensemble de points de la forme (x,y,z,t) de coordonnées entières et positives). La résolution du maillage est adaptative. En effet, le nombre d'éléments finis suivant chacune des coordonnées spatiales est déterminé par le rapport entre l'étendue spatiale, sur l'ensemble du flux de points, de cette coordonnée, et la somme des étendues de toutes les coordonnées spatiales. La coordonnée temporelle elle est déterminée par le nombre de nuages de points en entrée.
On détermine les résolutions en déterminant Xmin, Ymin et Zmin (respectivement Xmax, Ymax et Zmax) les valeurs minimales (respectivement maximales) des coordonnées des points. On applique alors à un facteur de résolution unique le ratio de l'étendue de chacune des coordonnées sur l'étendue totale, afin d'obtenir un maillage relativement cubique, dont la précision est déterminée par un facteur unique.
On peut ensuite adapter ces points afin de former un maillage tétrahédrique en 3D, voire hyper-tétrahédrique en 4D, au moyen de formules simples.
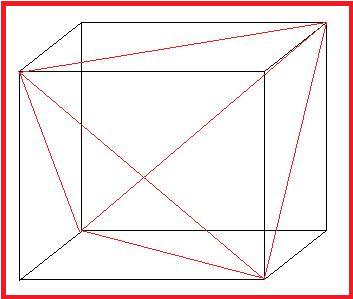
Découpage d'un cube en tétrahèdres 3D
Alors que découper un maillage cubique en maillage tétrahédrique reste assez simple en 3D (ici en 5 tétrahédre), il est bien plus difficile de découper en hyper-tétrahédre un hyper-cube. Afin de simplifier le maillage, nous ne remplirons pas entièrement l'hyper-cube, mais nous voulons tout de même que chaque face du cube soit recouverte, laissant l'intérieur des hyper-cubes vides et non utilisés par la méthode des éléments finies. De laisser des morceaux vides dans chaque hyper-cube n'a pas d'importance dans la méthode des éléments finies, puisque nous ne recherchons pas une méthode des éléments finies de grande précision Dans cet optique, en utilisant simplement les 16 sommets de l'hyper-cube, nous obtenons 8 hyper-tétrahèdres.
Les construire est assez simple, nous prenons simplement un des 16 points, et ses 4 points adjacents. Puis pour chaque face découpée en deux, nous prenons le point non utilisé et nous recommencons. Lorsque nous placons les points à l'intérieur des tétrahèdres, nous supposons que si le cube possède un point, alors le tétrahèdre aussi
La construction de ce maillage permet de facilement constituer la matrice recherchée dans la résolution du système linéaire.
Pré-traitement du maillage
Nous souhaitons déterminer une première ébauche de l'intérieur et de l'extérieur de l'objet, au moyen d'une interpolation de la fonction d'appartenance à l'objet, sur le maillage. Cette étape se subdvise en trois sous-parties :
Pré-initialisation
Nous initialisons les points du maillage comme étant indéfinis partout, si ce n'est aux endroits où des points de données sont présents, auquel cas les éléments du maillage correspondant sont étiquetés comme appartenant à la bordure de l'objet.
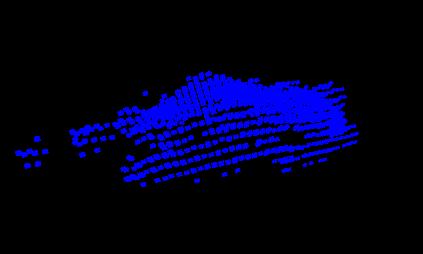
Bordure de l'objet
Première ébauche de l'intérieur et de l'extérieur.
Pour déterminer une première ébauche de l'extérieur de l'objet, nous déterminons l'enveloppe convexe du nuage de points donné, pour chaque image, en labellisant l'extérieur de cet espace convexe.

Enveloppe convexe
A.sharf suggère que nous cherchions à établir les maxima locaux de la fonction de distance aux points de données pour déterminer une première ébauche de l'intérieur de l'objet. Cependant, ces minima étant très peu nombreux et lourds à calculer, nous avons décider de déterminer ces points intérieurs en prenant le barycentre de trois points de données choisi aléatoirement, et un quatrième maximisant la distance aux trois autres points.
A l'issue de cette étape, nous disposons donc de points labellisés comme étant intérieurs à l'objet, extérieurs, et de points de bordure (les points donnés).
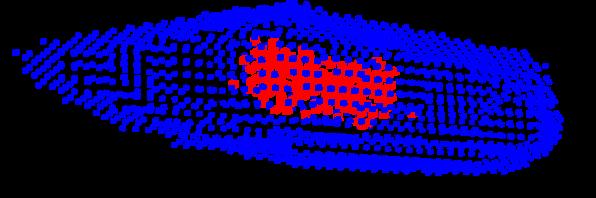
Première ébauche de l'intérieur à partir de l'enveloppe convexe
Raffinement des données : la méthode des éléments finis
On utilise ensuite la méthode d'interpolation de fonction implicite dans le contexte des éléments finis pour affiner notre ébauche d'intérieur/extérieur de l'objet.
Le principe est d'interpoler au mieux la fonction d'existence comme décrit dans Interactive Topology-Aware Surface Reconstruction. Nous avons adapté la méthode en fixant les poids à 1 pour les points étiquetés comme intérieurs ou extérieurs, et à 20 pour les points de la bordure.
Pour appliquer la méthode des éléments finis, nous devons de construire la matrice K. Il nous est expliqué comment la construire dans le cas d'un maillage 3D tétrahédrique. Afin de construire K, nous adaptons la méthode à un maillage 4D. Ainsi, nous calculons Jj = [x1-x5, x2-x5, ...; y1-y5, ... ; z1-z5, ...; t1-t5, ...] A partir, de cela, nous cherchons à résoudre afin d'obtenir les Ej. Ceci est rapidement retrouvé grâce à la méthode du Pivot de Gauss. Il nous reste à multiplier Ej par son dual afin d'obtenir Kj à un facteur près. Nous effectuons celà pour les 8 hyper-tétrahèdres constituant hyper-cube. Comme c'est un maillage régulier, il n'existe pas d'autre sous-matrice Kj à calculer. Enfin il reste à construire la matrice finale en fonction des différentes combinaisons de points existantes, et de la numérotation des points.
Une fois ces matrics construites, il ne reste plus qu'à utiliser CHOLMOD pour résoudre le système, et ainsi obtenir une interpolation de la fonction d'appartenance à l'objet Um.
Cette fonction est positive à l'intérieure de l'objet, et négative à l'extérieur (à l'inverse de ce qui a été décrit dans l'article). Nous pouvons dès exploiter cette fonction pour :
Remarque : les matrices Kj sont calculées à un facteur près (det(Jj)/6 dans le cas d'un maillage 3D), mais ce facteur n'a pas d'importance
Remarque bis : Dans le cas d'un maillage régulier, les Kj sont identiques par construction.
Remarque ter : Les librairies nécessaires à un fonctionnement optimal de CHOLMOD (Lapack, GotoBLAS et metis) n'étant vraiment pas adaptées à un environnement windows, nous avons donc dû nous en passer, au détriment de l'efficacité du programme, notamment en terme de mémoire.
Résultats :

Image après application de la FEM partielle
Nous n'utilisons que certains résultats partiels de la FEM. En effet, si l'on essaie d'étiqueter comme intérieur tous les points où Um>0, on obtient des résultats incohérents :
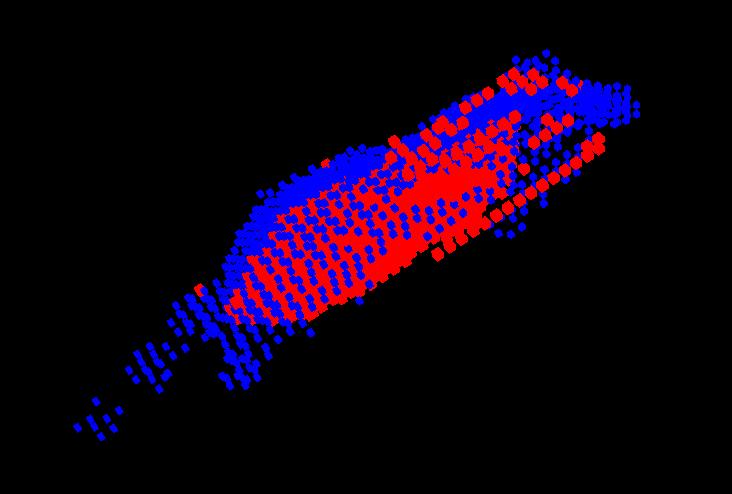
Image après application de la FEM complête
Nous avons également dû traiter la fonction Um après résolution du système car nous obtenions des résultats très étranges :

Protubérances en sortie de la FEM
Optimisation
Une fois les résultats précédents obtenus, l'article nous propose d'utiliser un procédé de résolution d'une équation des moindres carrés non linéaire à l'aide de la méthode Iteratively Reweighted Least Squares
Cependant, ayant été limités par le temps pour l'implémentation de cette résolution, nous avons décidé de prendre une autre direction afin d'essayer d'obtenir des résultats cohérents avant la fin du projet.
Nous avons utilisé une méthode de remplissage itérative de l'intérieur des objets dont le principe est le suivant :
Ce procédé est très rapide à calculer, et converge en général en ~200 itérations (quelques secondes de calculs pour une résolution moyenne), en labellant ~85% des points du maillage.
On obtient alors des résultats proches de l'intérieur recherché. Cependant, nous n'avons pas eu le temps d'intégrer aux itérations la régularisation dûe à la contrainte de conservation des flux.
Résultats :

Aperçu de l'objet en sortie du début de l'optimisation
L'intérêt est également que les zones non étiquetées sont celles se trouvant aux alentours de la bordure (entre l'intérieur et l'extérieur par "continuité" des valeurs itérées") Par conséquent, les intérieurs ainsi calculés peuvent servir de support à la résolution d'une équation de conservation de la masse et de minimisation des flux entre les images. En effet, les zones "clés" déterminées par cette méthode sont justement les zones de contestation qui ne sont pas encore étiquetées.

Aperçu des zones non initialisés
Evolutions et Améliorations
Nous n'avons pas pu mener à terme ce projet, notamment en raison de sa difficulté. Par conséquent il reste de nombreux points améliorables. En effet, comme énoncé précédemment, nos résultats actuels se prêtent relativement bien, à priori, à la résolution de l'équation de conservation de la masse, pilier de la méthode présentée par Sharf.
Cependant, cette avancée présuppose que l'on soit capable de résoudre des systèmes linéaires à base de matrices creuses encore plus volumineuses que celle vue dans la méthode des éléments finis. Par conséquent, le plus judicieux serait tout d'abord d'adapter les librairies Lapack, GotoBLAS et metis au projet, en configurant CHOLMOD (cf FEM) afin d'en tirer parti.
Ensuite, il faudrait exprimer le problème formulé par Sharf sous forme matricielle, le résoudre, et y inclure ensuite le terme de régularisation basé sur la conservation de la masse.
Enfin, une fois la plupart des éléments du maillage étiquetés (environ 95% selon Sharf), il convient alors de déterminer puis lisser la surface de l'ensemble des points intérieurs et de bordure pour obtenir le résultat désiré.
Le Layout de cette page web utilise le stylesheet de l'équipe "Antoine MELER & Adrien BERNHARDT" de l'année 2006.
top