Sujet 1 :
manipulation interactive de maillages en mouvement


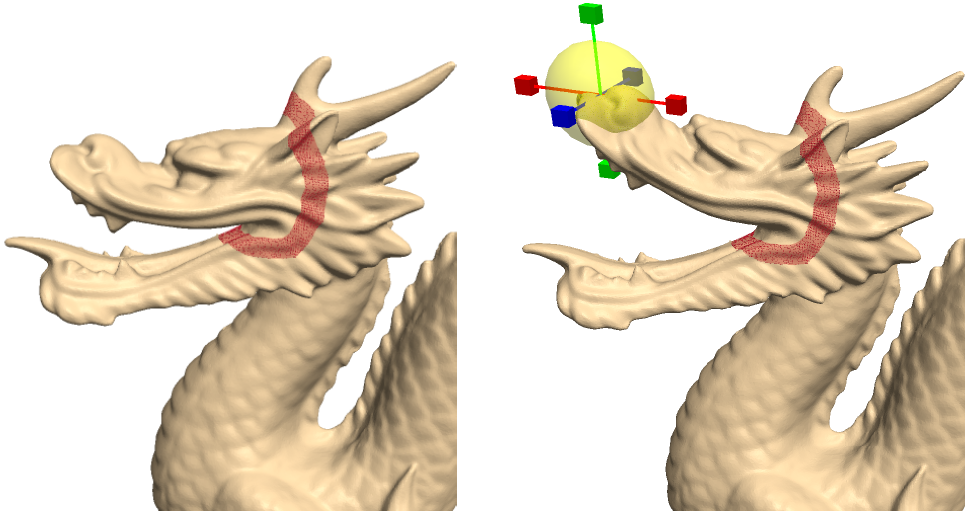
Laplacian editing
Déformation interactive d'un maillage statique [2]

Cadre du projet

Encadrant : Franck Hétroy.
Nombre d'étudiants : 2 à 4.
Lieu : le projet aura lieu en salle D200, ou équivalente, à l'Ensimag.
Prérequis : cours de la filière MMIS + cours d'algorithmique et de programmation de 1A et 2A.

Contexte

Il existe de nombreuses techniques pour déformer interactivement un maillage 3D, afin par exemple de créer de nouvelles poses, et éventuellement une animation. La plus populaire, que vous étudirez pour certains d'entre vous en troisième année dans le cours d'ingénierie de l'animation 3D, consiste à créer un "squelette d'animation", à déformer ce squelette puis à répercuter les déformations sur le maillage. En 2004 a été proposée une nouvelle technique [2], beaucoup plus simple pour l'utilisateur : celui-ci délimite la frontière de la zone à déformer puis sélectionne un sommet qu'il déplace (voir la figure ci-dessus). Les sommets voisins, dans la limite de la zone, sont déformés de manière assez naturelle : voir cette vidéo pour un exemple.

La méthode proposée dans [2] repose sur un concept simple : il consiste à travailler non pas sur les coordonnées globales des sommets du maillage, mais sur une représentation locale de ces sommets. A chaque sommet est associé la différence entre ses coordonnées et la moyenne des coordonnées des sommets voisins. C'est ce qu'on appelle les coordonnées différentielles du sommet. L'opérateur mathématique qui donne ces coordonnées différentielles à partir des coordonnéees globales est appelé, par analogie avec le cas continu, opérateur Laplacien du maillage. Le calcul des transformées de tous les sommets après une déformation revient à résoudre un système linéaire aux moindres carrés.

L'objectif du projet est d'étendre les concepts et méthodes introduits dans [2] au cas des séquences de maillages, c'est-à-dire aux maillages spatiaux-temporels. Ceux-ci peuvent être de deux types (voir quelques exemples ici) :
  1. en vision par ordinateur, on reconstruit un maillage (à partir de vidéos ou d'un scanner) indépendamment à chaque pas de temps. Il n'y a pas de cohérence temporelle entre deux maillages successifs (nombre de sommets et de faces et relations de voisinage entre sommets différents). On parle de séquence non contrainte ;
  2. en informatique graphique, on part d'un premier maillage qu'on déforme successivement. Tous les maillages obtenus ont donc le même nombre de sommets et de faces, et les relations de voisinage entre sommets sont préservées tout le long de la séquence. On parle de maillage dynamique.
Afin d'atteindre cet objectif, on étudiera la généralisation de l'opérateur Laplacien aux espaces de Minkowski (espaces avec une dimension temporelle) : l'opérateur d'Alembertien. L'objectif est donc d'obtenir une méthode qui permette de déformer interactivement à la fois en espace et en temps une séquence de maillages, à partir de la sélection d'un sommet sur un maillage de la séquence. Les applications possibles sont nombreuses : correction du mouvement d'un personnage, transfert du mouvement à un autre modèle, accélération ou décélération du mouvement, etc.

Travail demandé

  1. Lire et comprendre en profondeur l'article [2], ainsi que la notion d'opérateur d'Alembertien et les notions associées. L'article [1] vous est donné pour votre culture générale, il n'est pas primordial pour ce projet.
  2. Etendre les concepts d'opérateur Laplacien discret et de coordonnées différentielles aux séquences de maillages. On pourra se restreindre au cas le plus simple des maillages dynamiques.
  3. Etendre la méthode d'édition de maillages proposée par [2] au cas des séquences de maillages, et l'implémenter.
  4. Tester ces algorithmes sur différentes séquences de maillages. Des maillages dynamiques vous seront fournis ; pour des séquences de maillages non contraintes, voir le 4D repository de l'INRIA.
  5. Si le temps le permet, étudier l'extension d'autres méthodes présentées dans [1] au cas des séquences de maillages.
  6. Faire un bilan critique du projet.

Bibliographie

Détails techniques et liens utiles

La programmation se fera en C++, sous Linux.

Structures de données gérant les maillages

Je vous conseille d'utiliser la bibliothèque OpenMesh. CGAL est une autre bibliothèque beaucoup plus complète et un peu mieux documentée, mais elle nécessite un bon niveau de C++ (beaucoup de templates).

Logiciels utiles

L'usage d'un des deux logiciels suivants vous est fortement recommandé. Dans le cas où vous souhaiteriez développer vous-mêmes votre propre interface pas de souci, mais n'y passez pas trop de temps (ça n'est pas le but du projet !). Je peux vous fournir une mini interface graphique pour maillages statiques, qui tourne sous OpenGL, Qt et utilise libQGLViewer. Je vous conseille fortement libQGLViewer.
Pour les séquences de maillages, il existe Cortona3D.

Calcul matriciel

Voici trois bibliothèques standards, extrecirc;mement utilisées dans le domaine de l'informatique graphique.