Examen de synthèse d'images et d'animation

Licence professionnelle d'informatique, images et communication

Durée 1 heure. Calculatrice, documents de cours et tp autorisés.

1 Couleur et illumination (3 points)

Considérons une sphère centrée en $(0,0,0)$ vue par un observateur placé en $(0,0,5)$. Elle est illuminée par une lumière ambiante et une lumière directionnelle. Les paramètres sont les suivants:

• couleur de la sphère:
  • ambiante: 1.0f, 1.0f, 1.0f
  • émissive: 0.0f, 0.0f, 0.0f
  • diffuse: 1.0f, 1.0f, 1.0f
  • spéculaire: 1.0f, 1.0f, 1.0f
• couleur de la lumiere ambiante: 0.0f, 1.0f, 0.0f
• lumière directionnelle:
  • couleur: 1.0f, 0.0f, 0.0f
  • direction: -1.0f, -1.0f, -1.0f

Question 1

Représentez sur une figure la sphère sous forme d'un cercle, en ajoutant:

• le point où le reflet spéculaire est maximum (approximativement)
• la couleur en ce point
• une ligne représentant la limite de la zone éclairée par la lumière
• la couleur sur cette ligne

2 Formes et textures (4 points)

On désire représenter un dé à six faces comme un cube recouvert de la texture illustrée en figure . Les arètes du cube sont alignées avec les axes du repère local. La face 1 est dans le plan $z=1$, la face 3 est dans le plan $x=1$, la face 6 est dans le plan $z=0$, la face 4 est dans le plan $x=0$, la face 2 est dans le plan $y=1$, et la face 5 est dans le plan $y=0$. Le cube est défini par un QuadArray (tableau de quadrilatères) de 24 points.

Figure: La texture du dé.

Question 2

En respectant l'ordre des faces (1,3,6,4,2,5), écrivez le tableau des coordonnées des points. Pour une meilleure lisibilité, allez à la ligne à chaque fin de face. Pour chaque face, les points doivent être donnés dans l'ordre trigonométrique (inverse des aiguilles d'une montre).

Question 3

Écrivez de même le tableau des normales.

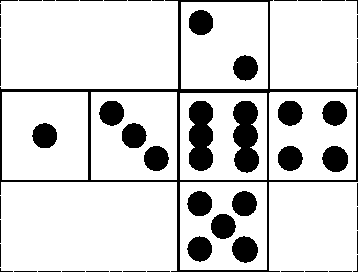
Question 4

Écrivez de même le tableau des coordonnées de texture correspondant à l'image donnée en figure .

3 Animation (3 points)

On désire animer un objet en translation passant successivement par les positions $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$. La figure schématise les positions successives de l'objet, ainsi que le graphe de scène le représentant. La translation suivant x est pilotée par un paramètre $\alpha_1$ et la translation suivant y par un paramètre $\alpha_2$. Le cycle s'effectue deux fois, à vitesse constante, chaque cycle durant huit secondes.

Figure: Positions successives de l'objet au cours d'un cycle, et graphe de scène associé.

Question 5

Représentez graphiquement les fonctions $\alpha_1(t)$ et $\alpha_2(t)$.

Question 6

On désire réaliser le même mouvement (2 cycles) sous forme d'une animation par positions-clés.

1. Donnez la liste des positions et dates de passage.
2. Dans le cas d'une interpolation non linéaire (trajectoire lissée), dessinez approximativement l'allure de la trajectoire.