Examen de Synthèse de Mouvement.
Maîtrise d'informatique. UJF-Grenoble

Durée 1h30. Tous documents autorisés.

30 Mai 2002

Versions imprimables:

PDF

ps.gz

On désire réaliser l'animation d'une voiture qui roule, effectue un créneau pour se garer, puis redémarre. Nous étudierons le modèle de la voiture, puis l'action de créneau et de redémarrage, puis l'enchaînement des actions.

Modèle de voiture

Nous utilisons un modèle simplifié composé uniquement d'une caisse et de 4 roues, sans suspension, comme illustré sur la figure 1.

Figure 1: Le modèle de voiture, composé d'une caisse rectangulaire et de quatre roues. À gauche, $(O,x,y)$ repésente le repère de la scène.

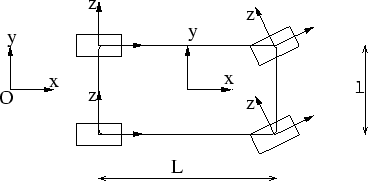
Le modèle possède les degrés de liberté (DDL) suivants:

• mouvements de la caisse: $t_x$, $t_y$, $\alpha$
• rotation des roues (roulement sur la route): $\theta_{avg}$ pour la roue avant-gauche, et de même, $\theta_{avd}$, $\theta_{arg}$ et $\theta_{ard}$
• rotation des roues pour diriger la voiture: $\phi_g$, $\phi_d$

Nous représentons la voiture par un graphe de scène au moyen de noeuds de types suivants:

• Repere : positionne le repère courant en translation et rotation
• Caisse : dessine une caisse de voiture centrée sur le repère courant, l'avant de la voiture dans la direction x, le haut dans la direction z
• Roue : dessine une roue centrée sur le repère courant, d'axe aligné sur z.

Dans chaque noeud de repère, on fera apparaître (en écrivant leurs noms) les DDL qu'il contrôle, ainsi que les valeurs L et l.

Question 1(4 points)
Représentez la voiture par un graphe de scène, en supposant que tous les DDL sont indépendants. Si possible, n'utilisez qu'un seul noeud Roue .

En réalité, les DDL de la voiture ne sont pas indépendants. On utilisera par la suite les hypothèses suivantes:

• à tout instant, toutes les roues tournent exactement du même angle (roulement)
• les deux roues directrices braquent exactement du même angle (direction)

Nous pouvons donc nous ramener aux DDL: $t_x$, $t_y$, $\alpha$, $\theta$, $\phi$

Question 2(6 points)
Représentez la voiture par un graphe de scène, en faisant apparaître ses cinq DDL dans les noeuds corresondants. Chaque DDL ne doit apparaître que dans un seul noeud.

Animation par positions-clés

La voiture, qui roule à une certaine vitesse, repère une place libre. Elle s'immobilise et effectue un créneau, comme illustré sur la figure 2. Nous désirons animer l'action de créneau par des positions-clefs.

Figure 2: Créneau. La voiture initialement en $0$ avec une vitesse non nulle passe par une position intermédiaire immobile $1$ avant de s'immobiliser définitivement en position $2$.

Question 3(4 points)
Pour chaque DDL, modélisez par des courbes de Hermite la trajectoire suivie ainsi que le contrôle de vitesse. On néglige la distorsion dûe au paramétrage, et on ne s'intéresse pas aux dates exactes des événements, qu'on placera arbitrairement sur l'axe du temps.

Le redémarrage s'effectue après un certain temps. Il consiste à repasser de la position 2 à la position 1 en accélérant progressivement.

Question 4(2 points)
Reprenez la question précédente, en l'appliquant à l'action de redémarrage.

Animation comportementale

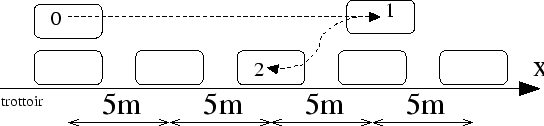
Nous désirons implanter le comportement suivant:

1. Le mouvement commence par une phase à vitesse constante le long d'une file de voitures garées, sans savoir à l'avance quelles sont les places libres
2. l'action de créneau est effectuée dès qu'une place libre est repérée, ce qui correspond à l'état 0 de la figure 2
3. la voiture repart une minute après la fin du créneau

Les voitures garées sont disposées régulièrement tous les 5 mètres le long d'un trottoir rectiligne orienté suivant l'axe x de la scène (fig. 2). Un tableau de booléens libre représente les places libres: libre[i] vaut vrai si et seulement si il y a une place libre centrée en x=5*i.

Le temps est représenté par une variable t .

Question 5(4 points)
Représentez graphiquement un automate de contrôle du comportement de la voiture. Précisez à quelle phase du mouvement correspond chaque état, et faites apparaître les conditions de transition.