Examen de Synthèse de Mouvement

UJF-Grenoble, M1-Informatique, option IG3D

Mai 2004

Versions imprimables:

PDF

ps.gz

Durée 1h30. À rendre sur copie séparée. Tous documents et calculatrices autorisés. La notation tiendra compte de la concision et de la qualité de rédaction des réponses. Le barème est indicatif.

Introduction

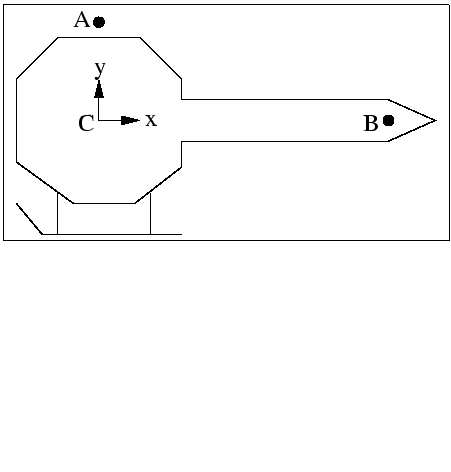
Dans ce devoir nous nous intéressons à la modélisation et à l'animation d'un hélicoptère. Il est composée de trois parties: la carlingue (figure ), une hélice principale accrochée en A et une hélice secondaire accrochée en B.

Figure: La carlingue de l'hélicoptère, dans son repère local centré au point C.

Modélisation

Nous désirons représenter l'hélicoptère sous forme d'un graphe OpenInventor. Nous allons modéliser une pale d'hélice, puis une hélice, puis l'hélicoptère composé de la carlingue et deux hélices.

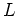Nous décidons de modéliser une pale d'hélice à l'aide d'un cylindre applati d'axe selon x et avec une extémité à l'origine du repère local comme indiqué sur la figure .a. La pale est paramétrée par sa longueur $L$, son grand diamètre 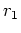$r_1$ et son petit diamètre 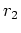$r_2$. Nous appliquons la ou les transformations géométriques adéquates à la primitive géométrique SoCylinder, qui trace un cylindre centré sur le repère local et aligné sur l'axe y, comme illustré sur la figure .b.

Question 1 (2 points)   Recopiez et complétez le sous-graphe de la figure .c représentant une pale d'hélice. Indiquez les valeurs numériques des transformations géométriques en fonction de $L$, $r_1$ et $r_2$.

Figure: Pale d'hélice.

Par la suite, on pourra représenter la pale par un seul noeud, correspondant à la racine du sous-graphe. Nous désirons maintenant repésenter l'hélice par assemblage de trois pales décalées de 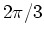$2\pi /3$, dans le plan (x,z) du repère local, et dont une est alignée sur l'axe x.

Question 2 (2 points)   Dessinez le sous-graphe correspondant à l'hélice. Faites apparaître les valeurs des transformations géométriques.

Par la suite, on pourra représenter l'hélice par un seul noeud, correspondant à la racine du sous-graphe. Nous désirons maintenant représenter l'hélicoptère entier. Nous disposons d'un sous-graphe carlingue qui modélise la carlingue conformément à la figure , qu'on pourra représenter par un noeud unique. L'origine du repère local est le point C(0,0,0). La pale principale est centrée en A(0,2.5,0) et dans le plan (x,z). La pale secondaire est centrée en B(7,0,0) et dans le plan (x,y).

La position de l'hélicoptère est représentée par les coordonnées x,y,z de l'origine de la carlingue, trois angles d'Euler 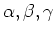$\alpha, \beta, \gamma$ associés respectivement aux axes x,y,z, et deux angles de rotation 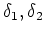$\delta_1, \delta_2$ pour l'hélice principale et l'hélice secondaire, respectivement.

Question 3 (6 points)   Dessinez le graphe de l'hélicoptère. Faites apparaître les données numériques disponibles ainsi que les noms des paramètres de position.

Animation

Les pales tournent à une vitesse constante de 30 tours/seconde pour la principale et 60 tours/seconde pour la secondaire. Elles sont animées par des SoCalculator prenant en entrée le temps et fournissant en sortie une valeur angulaire. Les angles doivent être compris entre 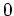$0$ et $2\pi$.

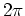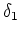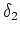Question 4 (1 point)   Représentez graphiquement les angles $\delta_1$ et $\delta_2$ en fonction du temps.

Question 5 (1 point)   Exprimez les formules de calcul de ces angles.

Nous désirons animer l'hélicoptère qui décolle, vole puis atterrit. Ce mouvement s'effectue en plusieurs phases comme illustré sur la figure :

• à t=0, il décolle verticalement du point A(50,2,0) puis infléchit sa trajectoire pour arriver horizontalement au point B(30,20,0) à t=10;
• entre t=10 et t=20, il vole horizontalement jusqu'à s'immobiliser au point C(10,20,0) pendant 5 secondes;
• entre t=25 et t=30, il atterrit verticalement pour s'immobiliser au point D(10,2,0).

Figure: Trajectoire de l'hélicoptère.

Question 6 (1 point)   Schématisez un automate de contrôle réalisant cette trajectoire.

Question 7 (2 points)   Pour chacune des phases du mouvement, indiquez et justifiez le type d'interpolation réalisé et les positions-clés.

Question 8 (1 point)   Pour chacune des phases du mouvement, représentez le controle de vitesse de l'hélicoptère.

Nous désirons maintenant donner un mouvement plus réaliste à l'hélicoptère. La force exercée par l'hélice principale étant perpendiculaire à celle-ci, nous devons l'incliner pour accélérer ou ralentir. On suppose que le rotor est fixe par rapport à la carlingue, il faut donc incliner tout l'hélicoptère. D'autre part, la résistance de l'air s'oppose à la vitesse de l'hélicoptère. Nous ne cherchons pas ici à faire une modélisation physique complète, mais juste à ajuster l'inclinaison de l'hélicoptère en fonction de son mouvement.

Question 9 (1 point)   Proposez une loi simple pour modéliser la force horizontale exercée par l'hélice en fonction de l'inclinaison de l'hélicoptère.

Question 10 (1 point)   Proposez une loi simple pour modéliser la résistance de l'air.

Les vitesses et accélérations n'interviennent pas explicitement dans nos lois de contrôle par positions-clés. Il nous faut donc les déduire des positions successives de l'appareil.

Question 11 (1 point)   Proposez une formule simple pour calculer la vitesse de l'appareil, et une pour son accélération.

Question 12 (1 point)   Proposez une formule simple pour calculer l'inclinaison de l'appareil à tout instant en fonction de sa vitesse et de son accélération.