
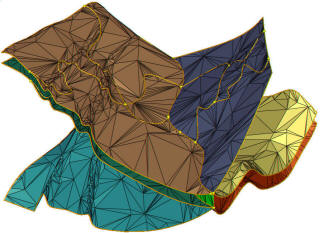
Topology Preserving Simplification of 2D Non-Manifold Meshes with Embedded Structures
Fabien Vivodtzev, Georges-Pierre Bonneau, Paul Le Texier
The Visual Computer, Vol. 21, No. 8, 2005.
Download a preliminary version
Click here for the final version.
Abstract: Mesh simplification has received tremendous attention over the past
years. Most of the previous works deal with a proper choice of error measures to
guide the simplification. Preserving the topological characteristics of the mesh
and possibly of data attached to the mesh is a more recent topic, the present
paper is about.We introduce a new topology preserving simplification algorithm
for triangular meshes, possibly non-manifold, with embedded
polylines. In this context embedded means that the edges of the polylines are
also edges of the mesh. The
paper introduces a robust test to detect if the collapse of an edge in the mesh
modifies either the topology of the
mesh or the topology of the embedded polylines. This validity test is derived
using combinatorial topology results. More precisely we define a so-called
extended complex from the input mesh and the embedded polylines. We show that if
an edge collapse of the mesh preserves the topology of this extended complex,
then it also preserves
both the topology of the mesh and the embedded polylines. Our validity test can
be used for any 2-complex
mesh, including non-manifold triangular meshes. It can be combined with any
previously introduced error measure.
Implementation of this validity test is described. We demonstrate the power and
versatility of our method with scientific data sets from neuroscience, geology
and CAD/CAM models from mechanical engineering.


Topology preserving simplification of a 2d non-manifold mesh with embedded polylines.
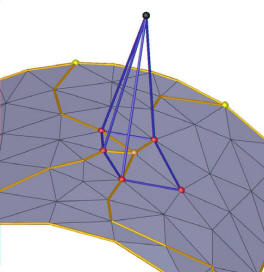
Link of a vertex on the intersection of several embedded polylines. In the extended complex, dummy triangles are added from the edge of the polylines modifying the link of the vertex as shown.
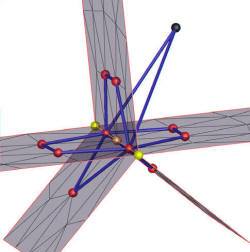
Link of a non-manifold vertex on the intersection of several surfaces.