TP3 : Champs vectoriels et Trajectoires

INF111-S2, UJF-Grenoble

1 Présentation

Le but de ce TP est de visualiser en 2D un champ vectoriel et ensuite de dessiner des lignes de flux à l'aide de particules. Aucune connaissance complexe en mathématiques n'est requise !
Néanmoins vous allez tout de même devoir utiliser des outils mathématiques tels que les vecteurs et l'intégration numérique (ce n'est pas un gros mot !). Pour vous faciliter le travail nous vous proposerons quelques rappels/explications au fil du TP, ainsi vous pourrez effectuer ce dernier sans ressortir vos cours de mathématiques.

Connaissances en algorithmique et programmation requises :

2 Les champs vectoriels

Définition:
Un champ est une fonction des variables (en 2D) du plan : $(x,y)$ ou (en 3D) de l'espace : $(x,y,z)$. Il caractérise une particularité de l'espace qui intéresse un observateur : la température dans une pièce, l'altitude sur une carte, la vitesse du vent à une certaine altitude dans l'atmosphère, les mouvements des plaques tectoniques sur la surface, ...

On peut séparer ces observations en deux catégories :

De manière plus formelle nous définissons un champ vectoriel grâce à une fonction $f:\Re^{2}\rightarrow\Re^{2}$. Par exemple la vitesse du vent (un vecteur donnant la vitesse "dans la direction des $x$ et des $y$ ") notée $\mathbf{v}$ en $x,y$ est :

\begin{displaymath} \mathbf{v}=f(x,y)=\left(\begin{array}{c} vx\\ vy\end{array}\right).\end{displaymath}

2.1 Objectif

L'objectif de cette première partie est de visualiser un champ vectoriel. Pour cela nous allons devoir dessiner des vecteurs sur notre feuille graphique.

2.2 Préambule

2.2.1 Utiliser la librairie Champ Vectoriel

Nous avons créé une nouvelle librairie C dans laquelle nous avons défini plusieurs fonctions. Pour les utiliser vous devez impérativement inclure le fichier champ_vectoriel.h dans votre projet de la même manière que pour logo.h ; vous devez aussi utiliser la librarie mathématique math.h. Pour ceci, ajoutez au début de votre programme :


\begin{singlespace} \texttt{\char93 include <champ\_vectoriel.h>} \par \texttt{\char93 include <math.h>}\end{singlespace}

2.2.2 Coordonnées dans la feuille de dessin

Nous allons utiliser la feuille de dessin comme un système de coordonnées. Si vous initialisez une fenêtre de taille 600x600 pixels, le pixel au centre de la feuille sera à la position $(x,y)=(300,300)$.

Attention : l'axe des $x$ va bien de la gauche vers la droite mais l'axe des $y$ lui va du haut vers le bas. Ainsi, le pixel "origine" à la position $(0,0)$ est situé en haut à gauche de la feuille.

2.3 Les vecteurs

Nous désirons créer une procédure permettant de dessiner un vecteur $\mathbf{v}$ (à partir d'une position $(x,y)$ sur la feuille graphique) sous forme de flêche.

Pour ce faire, nous dispons de deux nouvelles procédures logo (et leur équivalent en C) :

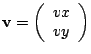Pour dessiner le vecteur vous devez orienter le curseur dans la bonne direction, en d'autres termes connaître son angle par rapport à l'horizontale. Pour calculer cet angle a étant donné le vecteur $\mathbf{v}=\left(\begin{array}{c} vx\\ vy\end{array}\right)$ il suffit d'écrire (en C) :


\begin{singlespace} \texttt{a =} \texttt{\textbf{-}} \texttt{atan2( vy, vx );}\end{singlespace}

(notez bien qu'il faut mettre $vy$ en premier paramètre et $vx$ en deuxième).

Attention : la fonction atan2(vy,vx) donne la valeur de l'angle en radiants !
Attention : comme l'axe des $y$ du repère est inversé sur la feuille, il faut utiliser l'opposé de l'angle.

Le vecteur $\mathbf{v}$ possède une norme : $\vert\mathbf{v}\vert=\sqrt{vx²+vy²}$. En C, pour calculer la racine carrée $rc$ d'un réel $r$ il suffit d'écrire :

rc = sqrt( r );

Question 1 : la procédure tracerVecteur

Ecrivez la procédure tracerVecteur répondant à la spécification suivante :

tracerVecteur( X, Y, VX, VY )

paramètres :
  • réels X, Y /* la position (X,Y) de "départ" du vecteur */
  • réels VX, VY /* le vecteur lui même : les 2 composantes en X et en Y */

spécification :
Dessine le vecteur $(vx,vy)$ depuis la position $(x,y)$. La pointe du vecteur possède une flèche (pour indiquer la direction du vecteur) de taille 5 et d'angle 30 degrés.

Question 2 : écrivez la procédure C correspondante.

Dans le langage C, la valeur de $\pi$ est stoquée dans la variable M_PI (ainsi pour obtenir la valeur de $2*\pi$ il faut écrire 2*M_PI).
Testez votre procédure pour vérifier qu'elle fonctionne correctement.

2.4 Le champ vectoriel

Nous désirons maintenant dessiner un ensemble de vecteurs correspondant à un champ vectoriel donné. Pour ceci nous mettons à votre disposition deux fonctions obtenirVX et obtenirVY définies ci-dessous :

obtenirVX( X, Y )

paramètres :
réels X, Y /* les paramètres $x$ et $y$ passés à la fonction mathématique $f$ permettant d'obtenir la valeur du champ vectoriel en $(x,y)$ */

spécification :
Retourne la composante $vx$ du vecteur $v=f(x,y)$


La définition de obtenirVY est similaire à part qu'elle retourne la composante $vy$ du vecteur $v=f(x,y)$.

Exemple d'utilisation de ces fonctions C :

x = 15.4; 
y = 23.7; 
vx = obtenirVX( x, y ) 
vy = obtenirVY( x, y ) 
printf( "Le vecteur retourné par la fonction en (%lf,%lf) est (%lf,%lf)\n", x, y, vx, vy );



Nous ne désirons pas visualiser la valeur du champ vectoriel en chacun des points (pixels) mais plutôt à intervales réguliers (par exemple tous les 20 pixels) que l'on peut imaginer comme une grille ou un quadrillage (par exemple de 20 pixels de côté pour chaque case).

Question 3 : la procédure dessinerChampVectoriel

Ecrivez la procedure dessinerChampVectoriel répondant à la spécification suivante :

dessinerChampVectoriel( L ) 
paramètres :
réel L /* La taille d'une case du quadrillage */

spécification :
Dessine les vecteurs associés au champ vectoriel défini par la fonction $f$ aux "sommets" du quadrillage (tous les L pixels en $x$ ET en $y$).

Question 4 : écrivez la procédure C correspondante

Testez la puis essayez d'autres fonctions mathématiques (voir l'annexe 4.1 pour la liste des "fonctions" que vous pouvez utiliser).

Figure 1: Exemple : champVectoriel( 50 )
\includegraphics{champ_vectoriel_small}

3 Les trajectoires

Le champ vectoriel que nous avons utilisé précédemment peut être considéré comme un champ de vitesse (par exemple la vitesse du courant à la surface d'une rivière) qui fera avancer une particule au fil du temps. Le chemin emprunté par cette particule est appelé trajectoire.

3.1 Objectif

L'objectif de cette deuxième partie du TP est de visualiser d'abord une, puis plusieurs trajectoires.

3.2 Tracé d'une trajectoire

Pour tracer une trajectoire vous devez considérer le curseur comme étant la particule transportée par le flux.
Nous désirons suivre la particule au cours du temps : si je prend une photographie de la rivière toutes les secondes, je vais pouvoir y repérer une particule flottant sur l'eau et ainsi tracer la trajectoire de cette dernière en reliant ses différentes positions dans le temps par des traits.


Si à un instant $t$ le curseur se trouve en position $(x,y)$ avec pour vecteur vitesse $(vx,vy)$ (donné par le champ de vitesse en $(x,y)$), il se trouvera à l'instant $t+dt$ d'après (dans l'exemple précédent, on prend une photo toutes les $dt=1$ secondes) à la position :

\begin{displaymath} \left(\begin{array}{c} x+dt*vx\\ y+dt*vy\end{array}\right).\end{displaymath}

De cette manière il est possible de faire avancer la particule (ici le curseur) au fil du temps, pas à pas, toutes les $dt$secondes : $dt$ est appelé le pas de temps. Partant d'un instant $t_{0}$ avec un pas de temps $dt$, le temps est discrétisé ("découpé") de la manière suivante :

$t_{0}=0$ secondes
$t_{1}=t_{0}+dt$
[...]
$t_{n}=t_{n-1}+dt=t_{0}+n*dt$.


A chaque instant $t_{i}$ la particule se trouvera donc à la position $(x_{i,}y_{i})$ avec une vitesse $(vx_{i},vy_{i})$. Cette vitesse est obtenue grâce aux fonctions obtenirVX(X,Y) et obtenirVY(X,Y).

Question 5 : la procédure tracerUneTrajectoire

Ecrivez la procedure tracerUneTrajectoire répondant à la spécification suivante :

tracerUneTrajectoire( X, Y, DT, N ) 
paramètres :
  • réels X, Y /* La position de départ de la particule */
  • réel DT /* le pas de temps (par exemple $0.5$ secondes) */
  • entier N /* Le nombre de pas à effectuer */

procédure utilisée :
tracerVecteur

spécification :
Trace en rouge la trajectoire obtenue par une particule démarrant en $(x,y)$ pour une "duréetotale" de N*DT secondes, par pas de temps de durée DT. Le tracé se fait vecteur après vecteur (il y a donc en tout N vecteurs).


NB : pour changer la couleur du trait, il suffit d'utiliser la procédure couleur(c) de la manière suivante :
couleur( "rouge" );

Question 6 : écrivez la procédure C correspondante

Testez votre procédure pour vérifier qu'elle fonctionne correctement.

Figure 2: Exemple : tracerUneTrajectoire( 100, 300, 2, 9 )
\includegraphics{trajectoire_small}

Question 7 : Faites varier les paramètres DT et N

Décrivez leur influence sur la trajectoire.

3.3 Tracé de plusieurs trajectoires

Nous désirons maintenant tracer plusieurs trajectoires en faisant "démarrer" les particules aux sommets d'un quadrillage (de la même manière que pour le tracé du champ vectoriel).

Question 8 : la procédure dessinerTrajectoires

Ecrivez la procedure dessinerTrajectoires répondant à la spécification suivante :
dessinerTrajectoires( L, DT, N ) 
paramètres :
  • réel L /* La taille d'une case du quadrillage */
  • réel DT /* Le pas de temps pour chaque trajectoire */
  • entier N /* Le nombre de pas à effectuer pour chaque trajectoire */

procédure utilisée :
tracerUneTrajectoire

spécification :
Dessine les trajectoires en "lançant" les particules depuis les "sommets" du quadrillage (tous les L pixels en $x$ ET en $y$). Chaque trajectoire possédera N pas de temps de longueur DT.

Question 9 : écrivez la procédure C correspondante

Testez votre procédure pour vérifier qu'elle fonctionne correctement.

Figure 3: Exemple : dessinerTrajectoires( 100, 1, 5 )
\includegraphics{trajectoires_small}

Question subsidiaire :

Que pouvez vous dire du dessin obtenu si l'on prend DT=1 et N=1 ?

4 Annexes


4.1 Liste des fonctions mathématiques utilisables

  1. obtenirVX et obtenirVY
  2. obtenirVX_FLUX1 et obtenirVY_FLUX1
  3. obtenirVX_FLUX2 et obtenirVY_FLUX2
  4. obtenirVX_FLUX3 et obtenirVY_FLUX3

4.2 Quelques exemples de visualisation de champs vectoriels et de trajectoires (sites web)

About this document ...

Page web générée avec latex2html
Mathieu Coquerelle 2005-01-28