TP7 : Courbes de subdivision
INF111-S2, UJF-Grenoble
L'objectif de ce TP est de créer et de faire dessiner à l'ordinateur
des courbes lisses au travers de la librairie logo.
La librairie logo permet de tracer des segments de droite
très facilement, nous l'avons vu dans le TP sur les champs vectoriels
et les trajectoires. Vous savez ainsi dessiner des polygônes et des
suites de segments (par exemple pour les trajectoires).
L'idée de ce TP est de donner à l'ordinateur quelques points formant
un suite de segments. Puis, à partir de cette suite, l'ordinateur
va calculer une courbe lisse s'en approchant et l'afficher à l'écran.
Sur un ordinateur, une courbe lisse peut être vue comme une suite
de segments minuscules, tellement petits qu'ils sont perçus comme
des points de la taille d'un pixel. Dans la suite, nous utiliserons
le mot courbe comme un terme désignant plus généralement une
suite de segments (même si l'aspect de cette courbe n'est pas lisse).
Si nous voulons dessiner une courbe, nous avons besoin de stocker
en mémoire la liste des points constituant les segments. Si une courbe
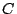 est constituée de
est constituée de 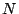 segments, elle possède donc
segments, elle possède donc 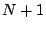 points.
Il est donc inenvisageable de créer
points.
Il est donc inenvisageable de créer 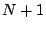 variables
variables 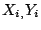 stockant la position de chaque point, imaginez que votre courbe possède
100 points ! Nous allons donc bien sûr utiliser des tableaux.
stockant la position de chaque point, imaginez que votre courbe possède
100 points ! Nous allons donc bien sûr utiliser des tableaux.
Une courbe est donc représentée par une suite de points stockés
dans deux tableaux : un tableau pour les X et un pour les Y.
Ces tableaux ont chacun une taille maximum de TAILLEMAX éléments.
Pour ce faire, vous devez ajouter la ligne suivante après les différents
#include :
#define TAILLEMAX 10000
où 10000 représente une taille assez grande (ne mettez pas trop ou
votre programme plantera).
Ecrivez la procédure tracerCourbe qui permette de
tracer une courbe à l'écran :
-
- tracerCourbe
paramètres :
- PX : un tableau de réels de taille maximum TAILLEMAX
- PY : un tableau de réels de taille maximum TAILLEMAX
- N : un entier : le nombre d'éléments effectifs de ces tableaux.
spécification :
Trace à l'écran les N-1 segments définis par la suite des N points dont
les coordonnées sont données dans les tableaux PX et PY.
Cette procédure pourra utiliser une procédure tracerSegment
similaire à tracerVecteur déjà écrite dans le TP sur les
champs vectoriels.
Testez votre procédure en créant dans le programme principal deux
tableaux contenant quelques points.
Il est fastidieux de rentrer dans le programme ou au clavier les coordonnées
des points dans les tableaux correspondants. Pour se simplifier la
vie, nous allons utiliser la souris pour enregistrer la position des
points.
La procédure lireClick va nous permettre d'obtenir la position
du pointeur de la souris au moment du clic. Cette procédure attend
un clic de la part de l'utilisateur dans la fenêtre logo et stocke
la position du clic dans ses paramètres une fois le clic effectué.
Voici un exemple d'utilisation :
-
- int X, Y;
lireClick( &X, &Y ); /* Attends que l'utilisateur clique dans la fenêtre */
printf( ''Clic dans la fenêtre logo à la position (%d, %d)\n'', X, Y );
Pour pouvoir utiliser cette procédure, vous
devez obligatoirement ajouter en haut de votre fichier (juste après
''#include <logo.h>'')
la ligne suivante :
void lireClick( int *x, int *y
);
Vous savez maintenant comment obtenir des positions sur l'écran simplement
à partir de clics de la souris.
Modifiez votre programme principal pour qu'il remplisse les tableaux
des coordonnées de N points au fur et à mesure, à partir des clics
de la souris. C'est vous qui fixerez N (par exemple si N=5 alors le
programme attendra 5 clics).
En 1974, George Chaikin a introduit une technique permettant de ''générer''
des courbes lisses à partir d'un petit nombre de points formant une
suite de segments : par abus de langage nous l'appelerons polygone
de contrôle. La technique appelée aussi Corner-Cutting consiste
à ''arrondir'' les coins de ce polygone (cf figure 1)
en subdivisant chaque segment.
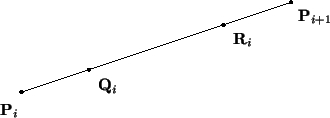
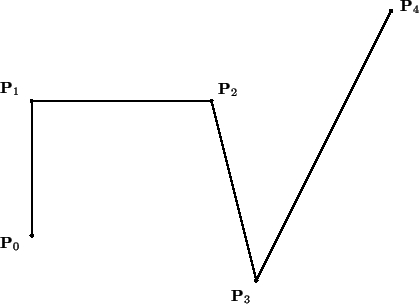
Figure 1:
Technique du Corner-Cutting
|
|
Etant donné un polygone de contrôle défini par un tableau de N points
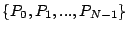 nous raffinons (subdivisons) ce polygone
de contrôle en générant un nouveau tableau de points :
nous raffinons (subdivisons) ce polygone
de contrôle en générant un nouveau tableau de points :
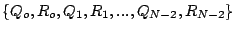 où chaque paire de points
où chaque paire de points
 est définie uniquement
en fonction des deux points
est définie uniquement
en fonction des deux points 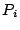 et
et 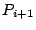 de la manière suivante
:
de la manière suivante
:
Il y a donc 2 nouveaux points pour chaque segments
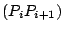 du
polygone de contrôle initial.
du
polygone de contrôle initial.
Ecrivez maintenant cet algorithme dans votre programme principal.
Voici quelques questions et remarques qui vous guideront :
- Etant donné un polygone de contrôle de N points, combien y aura t-il
de points dans le nouveau polygone de contrôle après raffinement ?
- Comment et où puis-je stocker ce nouveau polygone de contrôle ?
- Essayez tout d'abord de dessiner le polygone de contrôle initial et
ensuite le nouveau polygone de contrôle (d'une autre couleur) après
une subdivision.
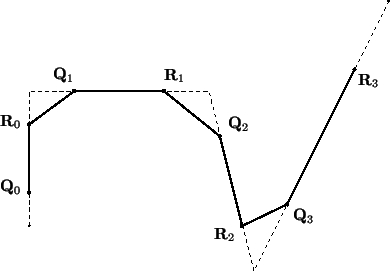
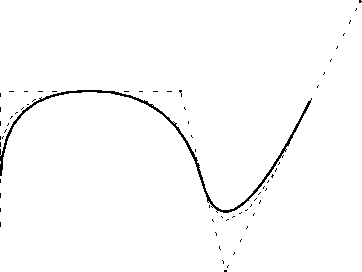
Figure 2:
Polygone de contrôle initial, après une subdivision et après de nombreuses
subdivisions
|
|
Le nouveau polygone de contrôle obtenu après subdivision peut lui
aussi à son tour être subdivisé, puis le nouveau polygone de contrôle
subdivisé à son tour, etc. A partir d'un polygone de contrôle 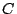 la courbe de subdivision associée est obtenue après une infinité de
subdivision :
la courbe de subdivision associée est obtenue après une infinité de
subdivision :
Nous ne pouvons calculer une infinité de subdivision : nous nous arrêterons
donc à un nombre M de subdivisions donné.
Généralisez votre algorithme pour effectuer M subdivisions successives
du polygone de contrôle : réfléchissez bien à la structure de votre
programme.
Remarque : au lieu de ne dessiner
que la dernière courbe calculée, vous pouvez toutes les afficher au
fur et à mesure en vidant l'écran entre chaque calcul et faire une
pause en utilisant la procédure attendre() avant de continuer
pour la subdivision suivante. Ainsi vous verrez l'évolution de votre
courbe au cours des itérations.
Dans la question précédente, vous effectuez M subdivisions successives.
Imaginons que M=1000, expliquez pourquoi votre programme ne marchera
plus et pourquoi, si il marchait encore, il ne servirait à rien de
faire autant d'itérations.
Trouvez un ou des critères (conditions) d'arrêt pour les subdivisions
de la courbe en fonction des remarques précédentes.
Nous souhaitons maintenant créer des courbes-polygones fermés. Un
polygone de contrôle fermé peut se traduire dans l'algorithme par
l'existence d'un segment supplémentaire entre le dernier et le premier
point de la liste : le segment
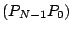 . Ce segment n'est
pas différent des autres, la seule nuance et dans l'indice des points
qui le forme : ce n'est pas simplement
. Ce segment n'est
pas différent des autres, la seule nuance et dans l'indice des points
qui le forme : ce n'est pas simplement 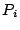 et
et 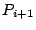 . Mais
sinon rien ne change !
. Mais
sinon rien ne change !
A vous de trouver comment incorporer ce nouveau segment dans le dessin
de la courbe et dans la génération du nouveau polygone à la subdivision.
Dans ce TP, nous avons utilisé 2 tableaux pour décrire une liste de
points : un tableau pour les X et un pour les Y. Il est possible de
voir un point comme un vecteur d'information : un tableau. Tout point
peut donc être stocké dans un tableau de taille fixe de 2 éléments.
En C :
-
- double UnPoint[2];
point[0] = 150.3; /* x=150.3 */
point[1] = 346.2; /* y=346.2 */
En C, il est possible de déclarer des tableaux de tableaux
: ceux-ci se rapprochent de la notion de matrices en mathématiques.
Il est alors possible de déclarer un tableau de points où un point
est un tableau de taille 2 :
-
- double Points[2][TAILLEMAX];
Points[0][I] = 546.3; /* x=546.3 pour le Ième point */
Points[1][I] = 14.5; /* y=14.5 pour le Ième point */
Ici, Points est considéré comme un tableau à deux
dimensions. Il n'est donc plus nécessaire de donner 2 tableaux à
une dimension en paramètre de la procédure ''tracerCourbe'' mais
maintenant un seul tableau à deux dimensions. La déclaration de la
procédure en C s'écrira donc :
void tracerCourbe( double Pointes[2][TAILLEMAX], int
N );
Effectuez les modifications nécessaires dans votre programme pour
n'utiliser que des tableaux à deux dimensions.
TP7 : Courbes de subdivision
INF111-S2, UJF-Grenoble
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers sujet.tex
The translation was initiated by Mathieu Coquerelle on 2005-03-23



Mathieu Coquerelle
2005-03-23