Simulation de fluides en 2D par particules de vorticité

1 Algorithme

1.1 Initialisation des particules

Il faut créer des particules là où la vorticité $\omega(x,0)$ n'est pas nulle. A l'instant $t_{0}$ la vorticité est non nulle lorsque $\nabla\mathbf{u}\neq0$ et lorsque $\varphi_{x}\neq0.$
Comme initialement dans notre simulation le flux est nul, il suffit de créer des particules d'intensité $\omega_{\mathbf{P}}=-\varphi_{x}\mid_{x_{\mathbf{P}}}$ pour les $x_{\mathbf{P}}$ tels que $\varphi_{x}(x_{\mathbf{P}},0)\geq\epsilon.$

NB : pour plus d'efficacité lors du calcul particules/particules, nous stockons $\omega_{\mathbf{P}}=-\varphi_{x}v_{\mathbf{P}}$ où $v_{\mathbf{P}}$ est le support d'une particule (ici $v_{\mathbf{P}}=vol=dx*dy$ ).

1.2 Distribution des particules sur la grille

Les particules sont distribuées sur la grille par projection de type spline (nommé M4') sur un support de $4\times4$ points sur la grille.
Soient $A_{i,j}$ les sommets de la grille où la projection a lieu et soient les $w_{i,j}$ les poids associé à chacun de ces sommets ; pour une quantité $Q$ transportée par la particule, nous obtenons les quantités $Q_{i,j}$ associées en chacun des sommets $A_{i,j}$ :

$$Q_{i,j}=Q\mid_{A_{i,j}}=w_{i,j}*Q$$

avec $w_{i,j}=a_{i}*b_{j}$ et :

$$a_{0}=\frac{(2-x_{0})^{2}(1-x_{0})}{2}$$

$$a_{3}=\frac{(2-x_{3})^{2}(1-x_{3})}{2}$$

$$a_{1}=1+\frac{x_{1}²(-5+3x_{1})}{2}$$

$$a_{2}=1+\frac{x_{2}²(-5+3x_{2})}{2}$$

et similairement pour les $b_{j}$ par rapport à $y$.

Ici les $(x,y)_{i,j}$ représentent la position relative de la particule $\mathbf{P}$ par rapport au sommet $A_{i,j}$ en ``unité de sommets'' : par exemple $x_{0}=1-x_{1}$ , $x_{3}=2-x_{1}$ et $x_{1}$ est la distance entre la particule et le sommet de coordonnées entières inférieures.

1.3 Calcul de la streamfunction $\Psi$

Le but est de résoudre l'équation de Poisson suivante :

$$\Delta\Psi=-\omega.$$

Pour ce faire il existe deux méthodes : la première par différences finies et la seconde en passant dans l'espace de Fourier.

1.3.1 Différences finies

Ici nous proposons une résolution de type explicite en partant de l'équation :

$$\frac{\partial²\Psi}{\partial x²}+\frac{\partial²\Psi}{\partial y²}=-\omega.$$

En développant à l'ordre 1, nous obtenons les $\Psi_{i,j}$ sur la grille de la manière suivante :

$$\Psi_{i,j}^{n+1}=\frac{\Psi_{i-1,j}^{n}+\Psi_{i+1,j}^{n}+\Psi_{i,j-1}^{n}+\Psi_{i,j+1}^{n}+h^{-1}\omega_{i,j}}{4}$$

où $h=dx*dy.$

La résolution se fait par un schéma itératif avec $\Psi$ initialement nulle en tout point et avec condition d'arrêt $max(\mid\Psi_{i,j}^{n+1}-\Psi_{i,j}^{n}\mid)<seuil$.

1.3.2 Espace de Fourier

Nous partons de l'hypothèse que le flux est périodique dans les deux directions. Nous pouvons alors résoudre simplement l'équation de Poisson dans l'espace de Fourier. Pour une fonction $f(x)$ nous noterons sa transformée de Fourier $\widehat{f}(\xi)$ telle que :

$$\widehat{f}(\mathbf{\xi})=\mathcal{F}f(x)=\int_{\mathrm{I\! R}}e^{-2\pi Ix\xi}f(x)dx$$

(où $I=\sqrt{-1}$).

Dans l'espace de Fourier, notre équation de Poisson s'écrit donc :

$$\frac{\partial^{2}\widehat{\Psi}}{\partial\xi_{1}^{2}}+\frac... ...tial^{2}\widehat{\Psi}}{\partial\xi_{2}^{2}}=-\widehat{\omega}.$$

En développant les dérivées secondes :

$$(I\xi_{1})^{2}\widehat{\Psi}(\mathbf{\xi})+(I\xi_{2})^{2}\wi... ...{2}\widehat{\Psi}(\mathbf{\xi})=-\widehat{\omega}(\mathbf{\xi})$$

nous obtenons :

$$\widehat{\Psi}(\mathbf{\xi})=\frac{\widehat{\omega}(\mathbf{\xi})}{\mid\mathbf{\xi}\mid^{2}}.$$

Sur une grille régulière il est donc facile de trouver $\widehat{\Psi}$ de la manière suivante :

$$\widehat{\Psi_{i,j}}=-\frac{\widehat{\omega_{i,j}}}{(\xi_{i}+\xi_{j})^{2}}$$

où $\xi_{i}$ représente la $i^{ème}$ fréquence dans l'espace de Fourier définit par la transformée, soit dans notre cas : $\xi_{i}=I\frac{2\pi i}{nx}.$

Il suffit maitenant d'inverser la transformation pour obtenir $\Psi(\mathbf{x})$ :

$$\Psi(\mathbf{x})=\mathcal{F}^{-1}\widehat{\Psi}$$

Attention : si l'on utilise un package de calcul de transformées de Fourier (par exemple avec Matlab ou FFTW) il faut faire attention à bien utiliser les fréquences positives ET négatives (l'indice $i$ du tableau dans l'espace de Fourier permet de définir les fréquences positives ET négatives) suivant la définition de leur transformation et la disposition en mémoire des données. De même, pour gagner en vitesse, la plupart du temps le résultat est non normalisé, avec FFTW il faudra diviser par $N=nx*ny$ pour obtenir le résultat correct après transformation inverse.

1.4 Calcul du champ de vitesses $\mathbf{u}$ à partir de $\Psi$

Par définition, nous avons :

$$\mathbf{u}=\nabla_{\times}\Psi=\left(\begin{array}{c} \Psi_{y}\\ -\Psi_{x}\end{array}\right).$$

Nous obtenons donc le champ de vitesse $\mathbf{u}$ par dérivation de la fonction stream.

1.5 Calcul de l'évolution de $\nabla \varphi$

La level-set étant transportée par le fluide, nous avons :

$$\frac{\partial\nabla\varphi}{\partial t}=-\nabla((\mathbf{\m... ...abla\varphi-\left[\nabla\mathbf{u}\right]^{T}\cdot\nabla\varphi$$

où $\left[\nabla\mathbf{u}\right]=\left(\begin{array}{cc} u_{x} & u_{y}\\ v_{x} & v_{y}\end{array}\right).$

1.6 Calcul de la tension superficielle $T$

La tension superficielle est fonction de la courbure $\kappa$ déduite de la fonction level-set $\varphi$ et du paramètre de tension $\tau$.
La courbure $\kappa$ est définie comme suit :

$$\kappa=\frac{\varphi_{y}^{2}\varphi_{xx}-2\varphi_{x}\varphi... ...\varphi_{yy}}{(\varphi_{x}^{2}+\varphi_{y}^{2})^{\frac{3}{2}}}.$$

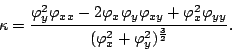
On peut maintenant définir la tension $T$:

$$T=\tau\kappa\nabla\varphi\delta(\varphi)$$

qui grâce à la fonction dirac $\delta(\varphi)$ a un support limité aux zéros de la level-set.

1.7 Intégration par Runge-Kutta 4

Pour plus de stabilité lors de l'advection sur les particules nous utilisons un schéma de type RK4. Si $x'=f(x,t)$, alors pour un pas de temps $h$ , soient :

$$k_{1}=f(x_{n},t_{n})$$

$$k_{2}=f(x_{n}+\frac{h}{2}k_{1},t_{n}+\frac{h}{2})$$

$$k_{3}=f(x_{n}+\frac{h}{2}k_{2},t_{n}+\frac{h}{2})$$

$$k_{4}=f(x_{n}+hk_{3},t_{n}+h)$$

Nous obtenons :

$$x_{n+1}=x_{n}+\frac{h(k_{1}+2k_{2}+2k_{3}+k_{4})}{6}.$$

Ce schméma est adopté notament pour trouver les vitesses en chaque particule à partir de la grille par distribution de la grille sur chaque particule (par la méthode (inversée) décrite en (1.2)).

Ensuite les particules sont déplacées et leur vorticité mise-à-jour selon :

$\frac{\mathbf{D}x_{\mathbf{P}}}{\mathbf{D}t}=\mathbf{u_{P}}$, $\frac{\mathbf{D\omega_{P}}}{\mathbf{D}t}=\tau T$- $\varphi_{x}$

$x_{\mathbf{P}}^{t+1}=x_{\mathbf{P}}^{t}+dt\frac{\mathbf{D}x_{\mathbf{P}}}{\mathbf{D}t}$ , $\omega_{\mathbf{P}}^{t+1}=\omega_{\mathbf{P}}^{t}+dt\frac{\mathbf{D\omega_{\mathbf{P}}}}{\mathbf{D}t}$

1.8 Transport de $\varphi$

La level-set est simplement transportée (advectée) par le fluide :

$$\frac{\partial\varphi}{\partial t}=-(\mathbf{u}\cdot\nabla)\varphi.$$

1.9 Remeshing des particules

Nous supprimons après chaque itération les particules ne transportant plus de vorticité car elles n'interviendront plus dans les calculs.
Pour ce faire, nous projetons à nouveau les particules sur la grille, supprimons les anciennes particules et en créons de nouvelles là où il y a de la vorticité (cf. Initialisation en (1.1)). Ces nouvelles particules repartent alors des sommets ``entiers'' de la grille.

About this document ...

Simulation de fluides en 2D par particules de vorticité

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers doc.tex

The translation was initiated by Mathieu Coquerelle on 2005-02-07