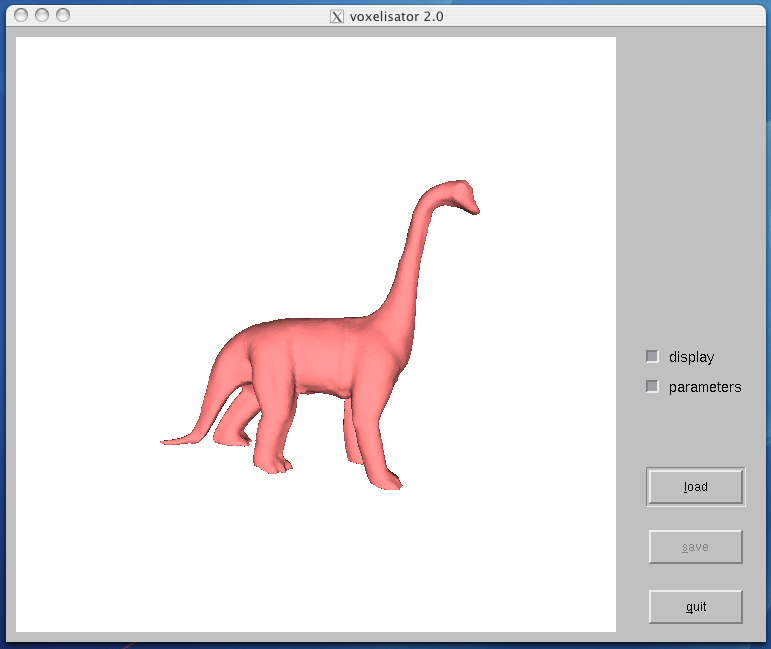
Compte Rendu Projet Image
Voxelisation d'une Scene Polygonale
Aujay Gregoire - Tournier Maxime
2005
Sommaire
- Introduction
- Description de l'algorithme
et résultats
- Ameliorations et
modifications
- A propos du programme
- Performances
- Bilan critique - Conclusion
1. Introduction
Le but de notre
projet était d'écrire un programme permettant la
voxelisation d'une scène
polygonale d'après l'algorithme proposé par D.
Haumont
and N.
Warzée en 2002
(site
officiel par ici).
Voxel
signifie
élément de volume (par analogie avec "pixel",
picture
element)
et
voxeliser un
objet, trouver tous les
voxels
(des "petits cubes") se trouvant à l'intérieur de cet
objet : on passe ainsi d'une représentation surfacique à
une représentation volumique.
Les interêts d'une telle représentation
sont :
- détection rapide de collisions
- simplification, réparation d'objets bruités (voir
le projet de Vincent Chaffard et de Philippe Gaussiaux)
- visualisation facile sur du matériel d'affichage 3D
Le point
délicat d'une voxelisation
est la détermination du statut des voxels : quelles
sont les parties de l'espace qui se trouvent à
l'intérieur des objets de ma scène et qu'elles sont
celles qui sont l'extérieur ? Lorsque la surface est
bruitée : avec des trous, des discontinuités, des
normales mal orientées, des chevauchements..., le travail
est encore plus
compliqué. L'algorithme que nous avons implémenté
permet justement de voxeliser une scène en prenant en compte les
trous et autres bruits de la surface.
Tuteur de Projet : Franck Hetroy
Outils utilisés :
- C++ (compilateur g++)
- QT
- OpenGL et QGLViewer
[retour sommaire]
2. Description de
l'algorithme et résultats
-a- L'espace va
être est
partitionné grâce à un Octree (arbre a 8 branches),
véritable pierre
d'angle de l'algorithme, il sera construit au fur et à mesure.
La
racine de cet Octree est le
plus petit cube qui contienne toute la scène. On divise
récursivement chaque cube (noeud de l'arbre) en 8 cubes
jusqu'à obtenir un arbre de la profondeur souhaitée. A la
fin, les feuilles de l'Octree qui
correspondent à des voxels,
contiendront toute l'information recherchée :
- des feuilles DISCARDED
: elles contiennent des ploygones de la scène originale
- des feuilles INSIDE
: elles sont à l'intérieur des objets de la scène
- des feuilles OUTSIDE :
elles sont à
l'extérieur des objets de la scène
Les sous arbres dont toutes les
feuilles ont le même statut seront supprimés et
remplacés par leur racine qui deviendra une feuille
(correspondant donc à une portion d'espace plus grand) portant
le statut correspondant. L'Octree
n'est pas complet on gagne ainsi en place mémoire et en temps
d'exécution pour la suite.
-b- La premiere phase
de l'algorithme consiste à trouver toutes les feuilles
DISCARDED.
Pour cela on se sert de la structure de départ : un
AABB Tree
que l'on nomme
INPUT TREE. Il
s'agit d'un arbre binaire dont les noeuds sont des boites englobantes
(AABB : aligned axis bounding box) qui englobent leurs deux fils, et
dont les feuilles contiennent les triangles de la scène,
englobés dans ces boites. Afin de gagner du temps les tests de
collisions se font avec les AABB ( test très rapide ) et
seulement si nécessaire avec les triangles (test couteux
même en utilisant l'algorihtme optimisé de
Tomas Akenine-Möller)
Ces cellules sont rejetées (discarded) car
elles ne peuvent pas être prises en compte par la suite de
l'algorithme elles sont vraissemblablement à la fois à
l'intérieur et à l'extérieur d'un objet.
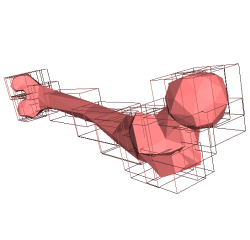
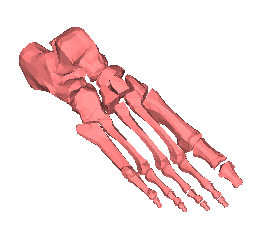
De gauche
à droite : un
fémur dans son INPUT TREE
(profondeur 5) puis les feuilles DISCARDED
(profondeur 6 et 8)
-c- Il faut ensuite
déterminer le statut des autres cellules. Le principe
utilisé est le suivant, on choisit d'abord une feuille dont on
détermine le statut : INSIDE
ou OUTSIDE. Cette cellule est
appelée racine (seed) car elle sert de point de
départ à la deuxième phase qui est la propagation
de ce statut aux feuilles qui sont dans la même potion d'espace
que la racine.
On
répète ceci jusqu'à ce que le statut de toutes les
feuilles soit déterminé.
2.1 Choix de la racine : seedChoice
Il ne faut pas
choisir la racine au hasard car elle doit pouvoir se propager le plus
possible aux autres feuilles. La racine est donc choisie la plus grande
possible afin de voir un maximum de feuilles et donc de leur propager
son statut. Si plusieurs feuilles ont la taille maximum, alors on
choisit celle qui est le moins entourée par des feuilles dont le
statut est déjà connu, on a là aussi plus de
chance de propager le statut. On introduit un poids, plus une feuille
contient d'information plus son poids est grand, il suffit alors de
choisir la feuille dont la somme des poids des noeuds rencontrés
en remontant jusqu'à la racine de l' Octree est la plus petite.
Nous avons utilisé un décor pour
chaque noeud de l'arbre. Celui-ci nous permet de trouver à
chaque fois la meilleure racine ( le poids, et la plus petite distance
à une feuille).
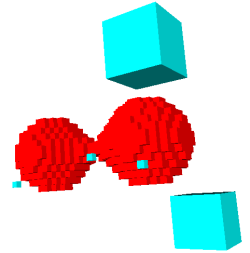
En cyan les feuilles qui ont
été élues racines extérieures et en orange,
les racines intérieures
2.2 Trouver le statut de la racine : solveStatus
On utilise
openGL pour
déterminer le statut de la racine. Pour cela, on place la
caméra au centre de la racine et on prend des "photos" de la
scène en regardant dans chaque direction (haut, bas, gauche,
haut,...). Ces six photos (
CubeMap)
vont nous permettre de déterminer le statut de la cellule. En
effet si on pouvait afficher en rouge les triangles dont les
normales sont dans le sens de la camera et en bleu ceux dont les
normales sont vers la caméra, le tout en tenant compte de la
profondeur alors une cellule à l'intérieur verrait du
rouge et une cellule à l'extérieur du bleu.
Et comme si c'était fait pour, cela est
possible en openGL, c'est du face culling. On peut donc à partir
des six photos estimer le statut de la racine.
On peut dire :
- dès que je vois du rouge je suis
INSIDE, c'est la stratégie
que nous appellons
NOHOLE,
car elle ne peut donner de bons résultats que lorsque la surface
n'a pas de trou. En effet si la surface à un trou, je v voir le
triangle intérieur par ce trou et donc du rouge.
à gauche
: un
exemple sans trou bien traité et à droite
: un modèle bruité donnant une
incohérence
- ou dès que je vois un
certain nombre de pixels rouges sur l'ensemble des 6 "photos" alors je
suis INSIDE. On peut ainsi
quand même avoir le bon résultat pour des surfaces qui ne
sont pas parfaites. Pour des modèles peu bruités, on
fixera ce paramètre à environ 80 % du nombre total de
pixels et pour ceux qui sont très abîmés, 25 %
donne des résultats souvent corrects. Il s'agit de la
stratégie que nous nommons HOLES.

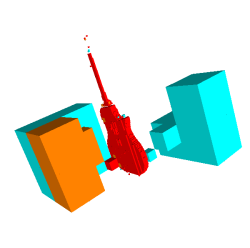
à
gauche : le
même que ci-dessus, bien traité par la stratégie
HOLES
à
droite : il reste
des incohérences dûes à de
gros défaut (ici beaucoup de normales sont à l'envers)
- on ne propage que si la feuille
à un statut défini de façon assez sûre.
On évite ainsi de propager une information dont on est pas
certain. On introduit alors un terme de confiance qui est
égal au nombre de faces sur lesquelles ont voit un nombre
donné de pixels rouges. On décide alors qu'une cellule ne
peut être
INSIDE qui si
son terme de
confiance est supérieur ou égal à 4 et elle ne
peut être
OUTSIDE que
si il est nul.


Un
modèle très bruité bien traité par
l'algorithme (profondeur 7)
2.2 Propager le
statut de la racine :
propagateStatus
openGL
va là encore nous être utile. En effet, comme pour le
solveStatus, on va prendre des
"photos" sur chacune des faces de la racine qui a été
retenue mais on s'interesse cette fois au buffer de profondeur (
depth buffer). Connaissant celui-ci
on peut propager le statut aux cellules qui sont dans le champ de
vision de la racine et qui ne sont pas cachées par les objets de
la scène.
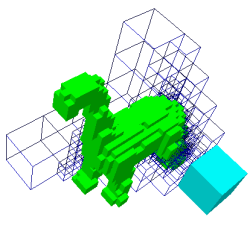
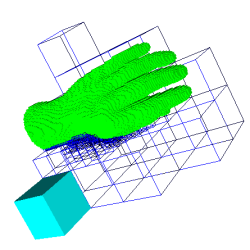 En fil de fer bleu, les
cellules qui ont reçu le statut OUSTIDE de la racine
après propagation dans une direction (vers les z>0).
En fil de fer bleu, les
cellules qui ont reçu le statut OUSTIDE de la racine
après propagation dans une direction (vers les z>0).
Afin d'éviter de marquer des feuilles
d'après une racine dont le statut est incorrect, on introduit un
terme de confiance de propagation. Ainsi une feuille ne reçoit
pas son statut qu'après avoir été vu par plusieurs
racines du même statut.
Ci-dessous une racine n'a pas propagé son statut
erroné, grâce au terme de confiance de propagation : les
feuilles voisines ont été vues qu'une seule fois par la
racine orange et plusieurs fois par les bleues.
Le terme de confiance permet de rattrapper
les erreurs du seedSolve.
L'algorithme
s'arrête lorsque l'on connait le statut de toutes les feuilles.
[retour
sommaire]
3.
Ameliorations
et modifications
3.1
Optimisations
Afin
d'optimiser le programme qui s'est avéré être
très lent et très couteux en place mémoire, nous
avons utilisé l'outil gprof
qui permet de connaitre quels sont les appels les plus frequents et le
plus couteux. De plus, nous nous sommes servi des optimisations que le
compilateur nous offre (déroulement des boucles : gain de temps
pour le parcours de l'arbre, car les boucles sont de taille fixe = 8 et
options d'optimisation de code). Au final, nous avons
amélioré la rapidité de l'ensemble des
opérations par un facteur voisin de 15.
En ce qui concerne les
améliorations que nous avons apporté, il y a :
L'utilisation des Display Lists
d'OpenGL qui permet d'améliorer grandement la vitesse de rendu
de
l'InputTree, et avec elle celle des parties de propagation et de
résolution du status.
Chaque
feuille de l'InputTree est associée à une Display List
qui est appellée
lors du trace.
L'utilisation
intensive du Frustum
Culling dans
toutes les operations de rendu. Cette technique permet de restreindre
le parcours de l'InputTree aux branches qui sont effectivement dans le
champ de vision, et d'ainsi de n'effectuer que le rendu de ce qui est
visible. Cette technique est également utilisée lors de
la propagation :
seules sont parcourues les branches de l'Octree visibles depuis la seed courante. Le gain de temps
lors du rendu est tres important.
La combinaison de ces deux optimisations nous ont
permis de réduire significativement
les durées de
rendus (de plusieurs minutes à quelques secondes, dans certains
cas).
Le décor de l'arbre se fait au fur et
à mesure que l'on trouve le statut des feuilles, on évite
ainsi de parcourir tout l'Octree
avant chaque choix de racine ce qui serait couteux ( O(8^n+1) où
n est la profondeur).
3.2 Eclairages de points obscurs
Un point important
qui n'est pas soulevé dans
la description de l'algorithme concerne les feuilles qui n'ont pas pu
devenir racine. Il se peut qu'à la fin leur statut ne soit pas
encore déterminé. En effet, si elle est
déclarée racine invalide, elle ne pourra jamais
l'être et si elle n'est pas vue par assez de feuilles d'un
même type, à cause du terme de confiance de propagation.
Nous avons donc décidé d'essayer
d'éliminer ce manque d'information.
On procède ainsi : on regarde si la feuille a été
vue par plus de INSIDE que de OUTSIDE, si oui elle acquiert le statut
correspondant.
(non codé :) Et
si
jamais elle a été vue par autant de feuilles de chaque
sorte alors on regarde le statut des fils de son père.
Et si après cela le statut est indéfini : pas de chance !
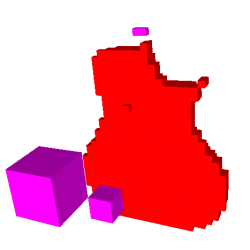
à gauche :
sans notre amélioration à droite :
avec notre amélioration on élimine les feuilles violettes
parasites
Nous avons également
pensé à une
technique de propagation de proche
en proche : une fois qu'une
cellule a acquis son status, il
peut etre intéressant de propager son status
immédiatement aux cellules
avoisinantes, sans se servir d'OpenGL. Cependant cette technique
comporte de nombreux inconvénients :
- Elle ne fonctionne que dans le cas
où la géometrie de depart ne
comporte aucun trou,
ce qui élimine du même coup le domaine de
prédilection de l'algorithme
proposé.
- S'il existe de nombreuses cellules
"isolées" au milieu de
cellules discarded, elles ne
pourront etre atteintes par cette propagation, par consequent il faudra
determiner leur status grace
a l'algorithme SolveStatus.
- Pour une propagation efficace, il
est nécessaire que toutes les
cellules de l'Octree aient la même taille. Dans ce cas, chaque
cellule
a au plus 6 voisines (on ne traite ici que les 6-voisines) et un simple
parcours de l'Octree permet de
définir les voisines de chaque cellules. Cependant, la
détermination
des voisines dans le cas de cellules de tailles inégales s'avere
nettement plus complexe. Cela entraine un important surcout, soit
à la
creation de l'octree, soit lors de la propagation, selon le moment ou
l'on calcule les voisines.
En résumé, et contrairement à ce que nous pensions
au premier abord,
cette technique ne presente pas de reel intérêt dans le
cadre de ce
problème. Peut-être en mettant en place un terme
d'atténuation : une feuille proche de la racine recevrait plus
d'information qu'une feuille éloignée....
Il nous parait possible de paralleliser cet algorithme en subdivisant
la scène puis en recoupant les informations, ou en
répartissant les directions de propagation, etc.
[retour sommaire]
4. A propos du
programme
Le programme se compose de 4 fenêtres :
La fenêtre principale où
l'on affiche les modèles dans un QGLViewer. Elle permet de
changer de mesh et de sauvegarder les Octrees calculés.
La fenêtre "param" qui permet de régler les
paramètres donnés au programme et de lancer les calculs.
La fenêtre "display" qui permet de régler l'affichage des
résultats qui se font dans la fenêtre principale.
La fenêtre rendu dans laquelle se trouve un QGLWidget et qui
affiche les rendus lors du solveStatus et du propagateStatus.
Il reste quelques problèmes
d'interface, des boutons qui ne s'enfoncent pas quand il faut, etc.
[retour sommaire]
5. Performances
Les tests ci-dessous ont ete effectues sur une machine
dont les
caracteristiques sont les suivantes:
Processeur Athlon 1,4GHz
~750Mo de memoire vive
Carte video NVidia GeForce3
Noyau Linux 2.4.27
Les durees sont exprimees en secondes.
Mesh dino.txt, 47 904
triangles:
|
Prof. 6
|
Prof. 7
|
Prof. 8
|
Prof. 9
|
Prof. 10
|
| Creation |
0
|
2
|
5
|
19
|
69
|
| Solving status |
2
|
3
|
4
|
8
|
16
|
Propagation
|
2
|
3
|
10
|
40
|
183
|
Mesh bones.txt, 4 204
triangles:
|
Prof. 6
|
Prof. 7
|
Prof. 8
|
Prof. 9
|
Prof. 10
|
| Creation |
0
|
0
|
1
|
6
|
23
|
| Solving status |
0
|
2
|
8
|
5
|
93
|
Propagation
|
1
|
4
|
18
|
79
|
471
|
La propagation demande un temps important car la
géométrie de la forme ne permet pas une propagation
efficace : beaucoup de parties cachées les unes par rapport aux
autres.
Mesh buddha-original.txt,
1 087 716 triangles:

|
Prof. 6
|
Prof. 7
|
Prof. 8
|
Prof. 9
|
Prof. 10
|
| Creation |
|
|
|
38
|
|
| Solving status |
|
|
|
610
|
|
Propagation
|
|
|
|
546
|
|
Nous obtenons un temps bien meilleur que celui annoncé sur le
papier, mais avec une machine un peu plus puissante.
[retour sommaire]
6. Bilan
critique
- Conclusion
Cet
algorithme c'est avéré être très robuste,
nous avons eu d'excellents résultats même sur des formes
très bruitées. Cependant dès que nous augmentons
la profondeur de l'Octree, le
coût en temps croît énormément, ce qui en
fait un algorithme très lent. Il existe des algorithmes beaucoup
plus rapide mais qui ne donne pas un aussi bon résultat dans
autant de cas que celui-ci. Il faudra choisir l'algorithme qui
correspond au du but visé, il n'existe surement pas d'algorithme
miracle !
Lors
de ce projet, nous avons perdu un peu (beaucoup) de temps à
régler des problèmes dûs à openGL mais cela
nous a permis, en mettant les mains dans le camboui, de mieux
comprendre le fonctionnement de ce précieux outil.
[retour
sommaire]
Dernière version: Vendredi 17 Juin 2005