Projet Image


Trois Algorithmes de Calcul de Plus Court Chemin







Marant Arnaud

Brondolin Cyrille

Espitalier Vincent





Sommaire :



Introduction



Principe des Algorithmes:



La phase de conception:




Comparaisons & tests des différents algorithmes





Introduction:


Le but de notre projet était d'implémenter plusieurs algorithmes de calcul de plus court chemin sur surfaces 3D. Ces algorithmes ont été décrits dans les articles suivants :


Les algorithmes de calcul des plus cours chemin sont utiles notamment lorsqu'on veut connaître en un temps très cours tous les chemins et distances à partir d'un point donné. Il suffit de calculer un fois pour toute la distance et le chemin de certains points caractéristiques (ces points dépendent des algorithmes utilisés). Alors pour n'importe quel point de la surface, il suffit de prendre le point caractéristique proche qui minimisera la distance du chemin depuis la source passant par ce point caractéristique. On connaîtra alors ce chemin bien plus rapidement que si on repartait de zéro pour chaque point que l’on veut examiner.


Ces algorithmes sont utiles notamment dans la cartographie, par exemple si on veut aller à un sommet d’une montagne modélisée. Cet algorithme nous permet de trouver très efficacement de quel endroit on peut partir, car on peut tester rapidement la distance d’un point de départ au sommet et le chemin le plus court à partir de celui-ci. On peut aussi utiliser ces algorithmes dans la conception et l’analyse de formes 3d.


Il faut préciser que le calcul de plus court chemin 3D diffère du calcul classique en 2D : En effet, on ne se déplace plus uniquement selon les arêtes (sinon un « lassique Dijkstra » aurait suffit), mais aussi selon les faces (ici triangles ou carrés).



  1. Principe des algorithmes :

    1. Idée générale :


L'idée générale des algorithmes est à peu de choses près toujours la même même si leur imprémentation diffère beaucoup : On effectue un genre de parcours en largeur avec une file de priorité qui contient des éléments de type arête ou des morceau d'arêtes, ordonnée selon leur distance minimale. On retire l'élément e « le plus proche » du sommet source (de dmin minimal) et on effectue des calculs sur les arêtes voisines ei de cet élément (recalcul des distances en passant par e, et si nécessaire, correction des distances des ei et mise dans la file de celles-ci ou de morceaux de celles-ci.

Ce calcul nous renseigne sur la fonction distance de chaque arête e au sommet source s (fonction qui associe un point M de e à un double dmin). Connaissant cette fonction pour toutes les arêtes, on peut déterminer la distance minimale d'un point a l'intérieur d'une face via un calcul élémentaire.


La méthode pour enregistrer les distances des arêtes et le type des éléments de la file caractérise les algorithmes, comme nous allons le voir.



Algo 1 : Arêtes discrétisées :


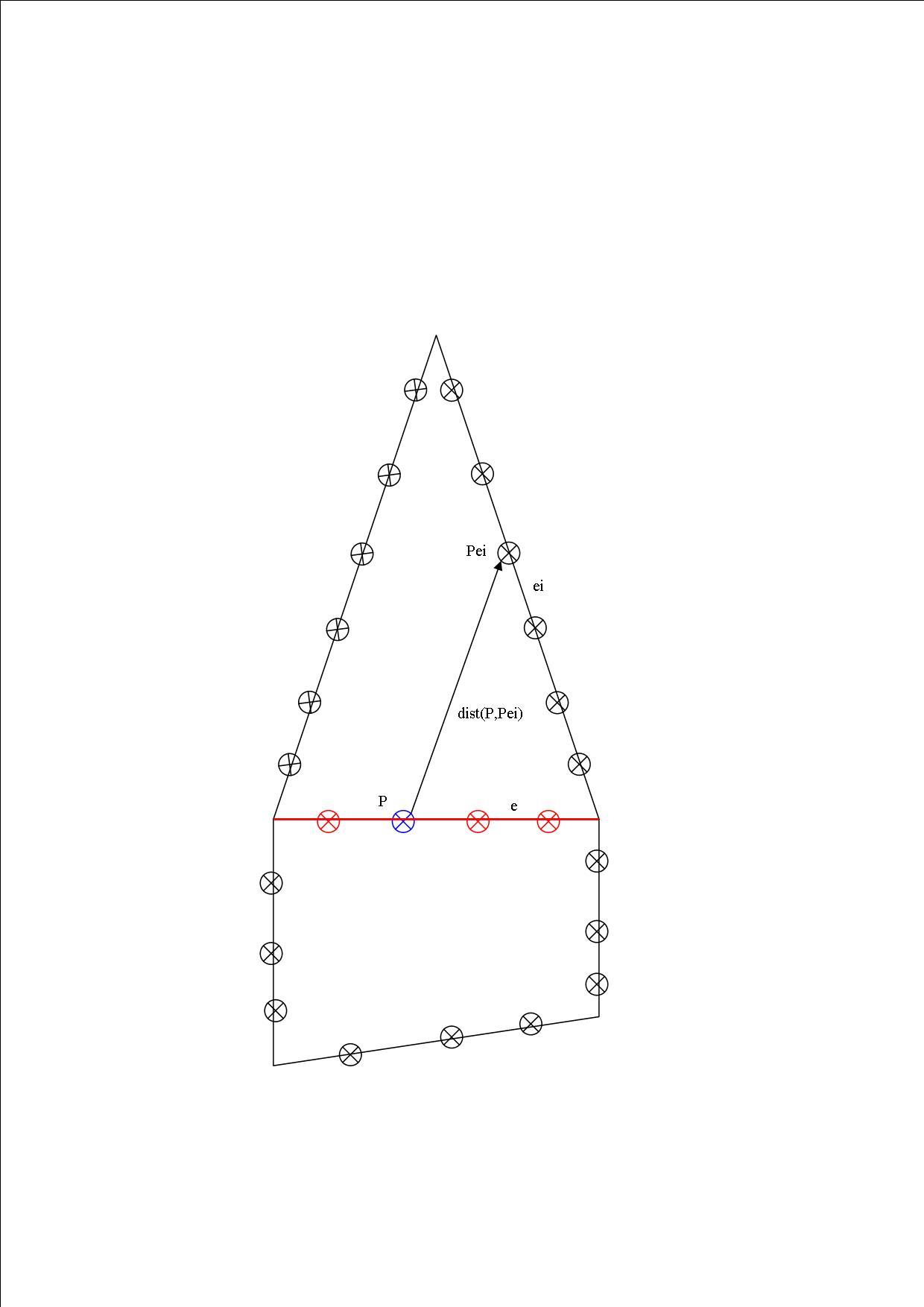
Ici, on découpe chaque arête en un certain nombre de points P selon un pas que l'on règle. Chacun de ces points à un attribut dmin qui va être minimisé au fur et à mesure de l'algorithme. Un attribut précédent permettra par ailleurs de tracer les géodésiques approchées.


La file contient des arêtes. Au départ, elle est initialisée avec les 3 (ou 4) arêtes autour du point source. Les dmin de ces arêtes sont égales aux distances des points a la source. (calcul exact ces points se situent sur une même face). Les dmin des autres points sont initialisées à +infini (ou une très grande valeur). Ensuite, on suit le principe suivant :


On retire l'arête e qui a le point de plus petit dmin parmi toutes les arêtes. Cela permet de faire un parcours en largeur et d'éviter trop de mises à jour des distances des arêtes dûes à un parcours chaotique.

Pour chacun des points P de l'arête e, on calcule la distance d qu'il aurait en passant par chacun des points Pei d'une des arêtes ei, autour de e (les arêtes ei appartiennent à l'un des 2 surfaces que e délimite). Si la distance d est inférieure à dmin (distance minimale courante de P), alors on améliore dmin, on corrige la « pseudo » géodésique, et on met l'arête ei dans la file :

dmin = d

prec(P) = Pei

Push(ei)



L'algorithme s'arrête quand la file est vide : on ne peut plus améliorer les distances des arêtes.


Ensuite, pour tracer les pseudo-géodésiques, on effectue une boucle sur tous les points P de toutes les arêtes : On trace pour chacun d'eux, la ligne qui le relie a son précédent.




Algo 2 : Intervalles :


Cet algorithme exact se base sur la propriété suivante : Le plus court chemin d'un point source s à un autre point P sur une surface en 3D est une droite une fois que l'on a déplié le modèle selon les faces adjacentes des arêtes traversées par le plus court chemin. Une fois que le modèle est aplati, les points P' qui sont « vus » par P traversent les même arêtes. On enregistre la distance des points P des arêtes du modèle. Un calcul élémentaire permet de retrouver la distance dmin des points P se trouvant à l'intérieur des surfaces élémentaires.

Ainsi, les ensembles des points (situés sur les arêtes) qui voient la source s une fois le modèle déplié sont des intervalles (des morceaux d'arêtes). D'ou le nom de l'algorithme. La file de priorité contient des éléments de type intervalle. On l'initiale en mettant les intervalles (qui sont en fait les arêtes) qui entourent s, comme pour le premier algorithme.

Dans la boucle de Dijkstra, on prélève l'intervalle p de distance minimale, on le « propage » sur les arêtes ei autour de e, qui sont dans le sens de la propagation. On en déduit de nouvelles fonctions distances pour les arêtes ei, qui se caractérisent par une listes d'intervalles. On compare les nouvelles distances aux anciennes, et on prend les meilleures (on fait un mix des 2 si c'est optimal). Cette dernière étape s'appele l'intersection des intervalles. On rajoute les nouveaux intervalles calculés sur les ei à la file si il y a amélioration, et on supprime de la file les intervalles qui ont été fragmentés par un éventuel mixage. On va détailler ces deux étapes cruciales que sont la propagation et l'intersection, après avoir précisé les structures de données.




Structures de données utilisées dans cet algorithme :


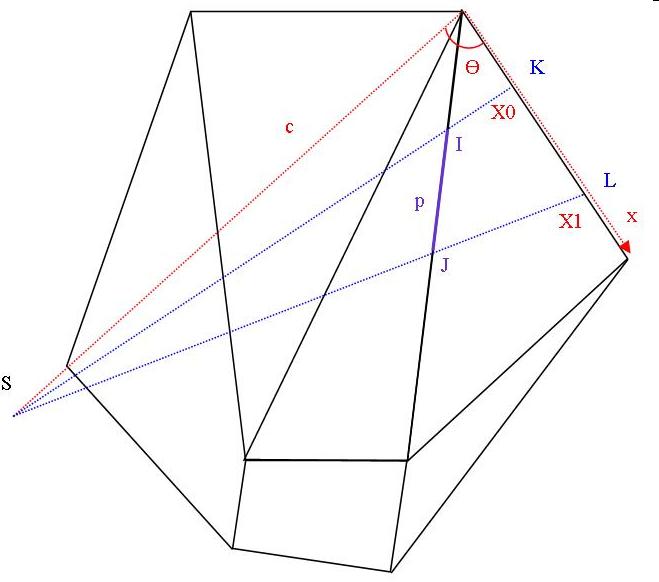
On définit un intervalle p comme étant une structure ayant pour attributs :




Propagation d'intervalle :


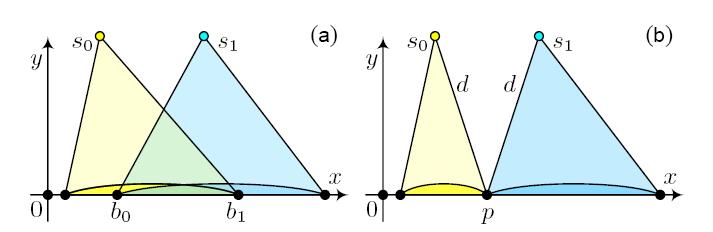
On a une arête ei qui appartient à la même surface que l’arête e (qui est l’arête de p). Le but de la propagation est de calculer les 3 intervalles qui vont découper ei (Figure 3 page 6). Sur la figure ci-dessous, c’est AK, KL, LB. On remarque que l’on peut n’avoir qu’un seul ou 2 intervalles et non 3. Exemple : CB n’en aura qu’un.



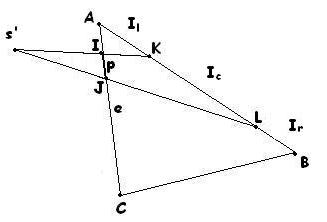
Pour découper une arête ei et trouver les 1, 2 ou 3 intervalles, on doit calculer l’intersection de (s’I) avec (AB) après avoir mis tous les points dans le même plan (résolution de systèmes 2x2…). Cela nous donne K. On fait la même chose avec (s’J) et on obtient L. Il ne reste plus ensuite qu’à regarder si K est dans le segment [AB]. Pour cela, on étudie l’ordre des points A, K , L, B (avec des produits scalaires) et on en déduit le nombre d’intervalles et leurs caractéristiques. (cf fig. 3 p. 6).

Une fois que l'on a les 3 intervalles, on leur affecte les attributs s', c, d, theta, prec de la facon suivante (on prend l'exemple précédent): KL voit s' directement à travers IL donc la source s' de KL sera la source s' de IL. AK aura comme source le point I, et LB le point J. On en déduit les paramètres d, c, theta.



Intersection d'intervalle :


Une fois que la propagation de p a été calculée, on compare les intervalles obtenus avec les intervalles précédents. On va chercher les points ou le points (il peut ne pas y en avoir) qui ont mêmes distance sur l'intersection des intervalles. On prend alors le meilleur des intervalles sur chacune des parties entre les points.






Algo 3 : « Flat-Exact » Algorithme :


Dans cet algorithme, on fait la simplification suivante : un intervalle = une arête. Pour calculer la fonction distance sur l'arête, il suffit de connaître les dmin des sommets de l'arête (d=0). C'est pour cela que le but de l'algorithme n'est que de chercher les dmin des sommets du modèle. Mais cet algorithme approximatif est plus compliqué qu'un Dijkstra sur les arêtes.


On stocke dans la pile des éléments de type arête, auxquels on adjoint un double dmin. A l'initialisation, on stocke les 3 arêtes qui entourent le point s. Au début de la boucle de Dijkstra, On prélève une arête e.

On doit alors étudier les arêtes {ei} qui sont autour de e, dans le sens de propagation. Comme on l'a vu, la fonction distance d'une arête est parfaitement déterminée par les attributs dmin de ses sommets. On propage seulement e en calculant la distance dmin des sommets M des arêtes {ei} au point source s en passant par e : Si s voit M alors la distance est la distance euclidienne (après s'être ramené dans un plan). Sinon, M n'est pas dans le champs de visibilité de s, on fait comme dans l'algorithme 2, on passe sur le bord de l'arête e: dmin(M) = min (d(s,I) + d(I,M) , d(s,J) + d(J,M)), ou I et J sont les sommets de l'arête e.


Si le dmin(M) calculé est meilleur que le dmin courant, alors on le corrige, et on rajoute à la file toutes les arêtes adjacentes à M.



  1. La phase de conception :

    1. Organisation du travail / répartition :

Pendant les 2 premières semaines, nous avons découvert CGAL et le principe des algorithmes de calcul de plus court chemin. 2 personnes ont implémenté le permier algorithme pendant que la 3éme a traduit les autres algorithmes, a fait des documentations et a implémenté des fonctions classiques utiles pour les algorithmes suivants : produit scalaire, vectoriel, norme, angle 3D, calcul d'intersection de droites dans un plan.
Ensuite, nous avons plutôt travaillé chacun sur un algorithme même s'il est arrivé que l'on s'entraide mutuellement pour faire du débuggage.



    1. Mise au point des algorithmes :

Les algorithmes 1 et 3 ont été les plus rapides à mettre au point (environ 400 et 550 lignes).

Cela est certainement dû à leur faible complexité de calcul (contrairement à l'algorithme 2). En effet, l'algorithme 2 faisant intervenir beaucoup de calcul numérique, géométrique (intersection de droites, calculs de position sur un segment). Les approximations numériques nous ont posé pas mal de problèmes (un double qui doit valoir 1, après calcul, ne vaut plus 1), et on a dû utiliser des epsilons : si d est un double inférieur à .001 alors, on considère qu'il vaut 0 par exemple. Ces erreur de calcul généraient parfois des intervalles de taille nulle, ce qui peut sembler curieux... On a par ailleurs mis des tests à l'entrée des fonction élémentaires : lors de l'intersection de 2 droites identifiées par les points A,B et C,D, on teste si A = C (ou A = D ou B = C ou B = D). Si c'est le cas, pas besoin de calculs, on renvoie directement le point d'intersection, A (respectivement ou B).


3) Comparaisons & tests des différents algorithmes :


-test de temps de calcul sur différentes surface:


(Pour l'algorithme 2 on emploie un epsilon = 0.01, qui permet de limiter la taille des intervalles à 0.01.Car si l'on ne se fixe pas cette limite d'une part l'algo ne se termine pas à cause des imprecisions de calculs de la librairie standard de math en c++, et d'autre part si epsilon est trop faible la taille mémoire necessaire devient tres importante.











-test d'utilisation mémoire sur différentes surface:






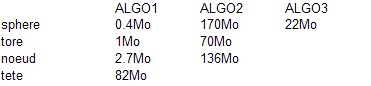
La taille memoire de algorithme 1 est d'après nos structures, linéaire par rapport à la taille du modèle. Alors que l'algorithme 2 est lui, plus dépendant de la forme des figures plus que de leur taille (on constate ce phénomène sur les tests ci-dessus).


-Isodistances:


Pour valider les différents algorithmes, nous avons commencé par comparer la position des courbes isodistances renvoyées par les différents algorithmes.




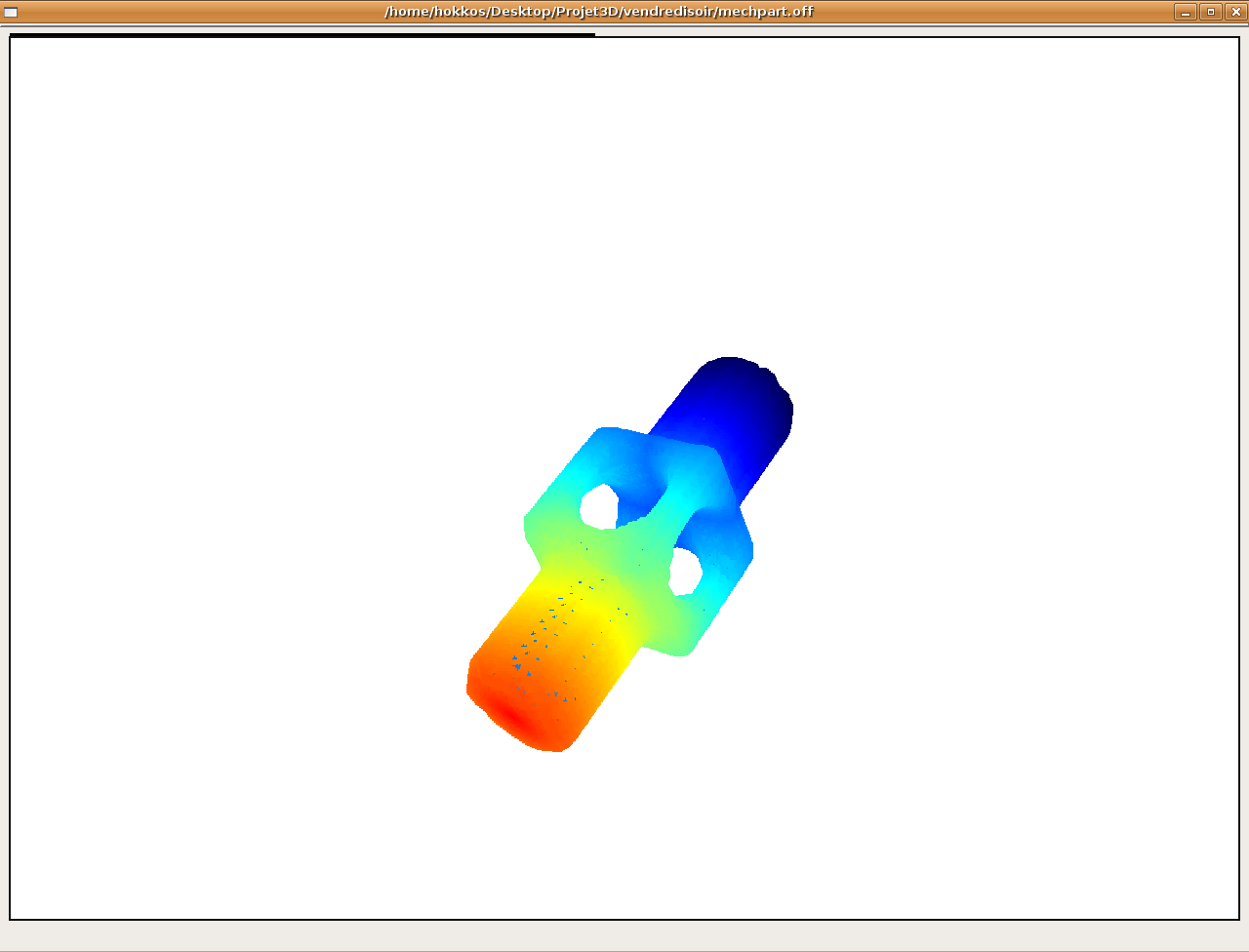
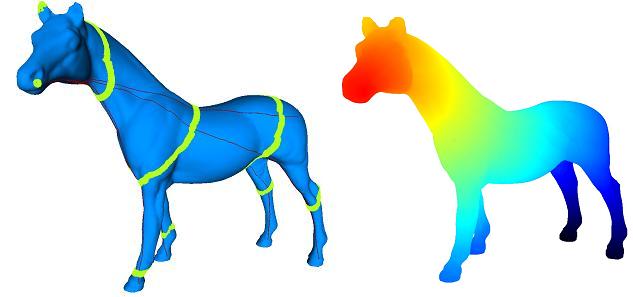
Figure obtenue par l'algo1 (la couleur est fonction de la distance à la source)







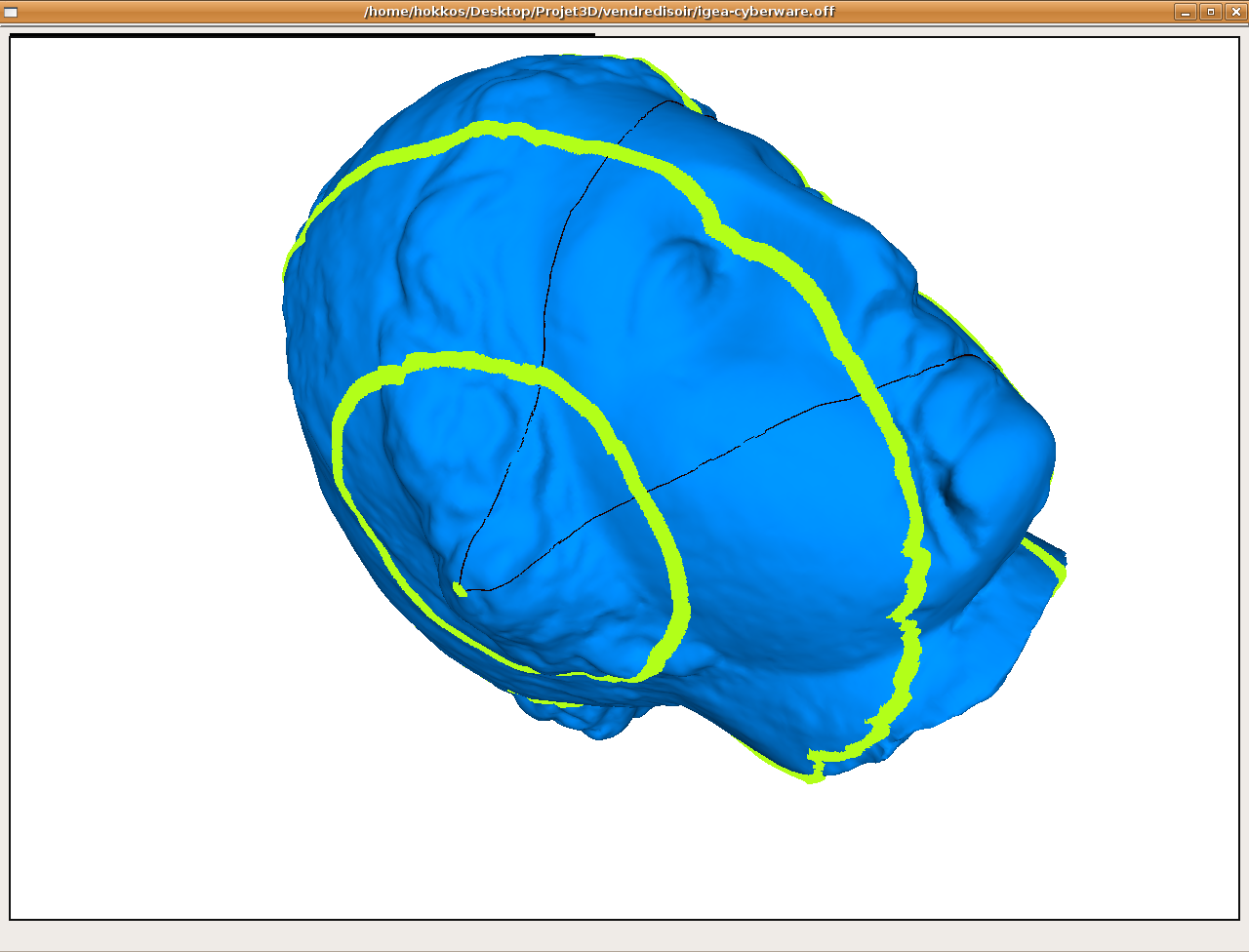
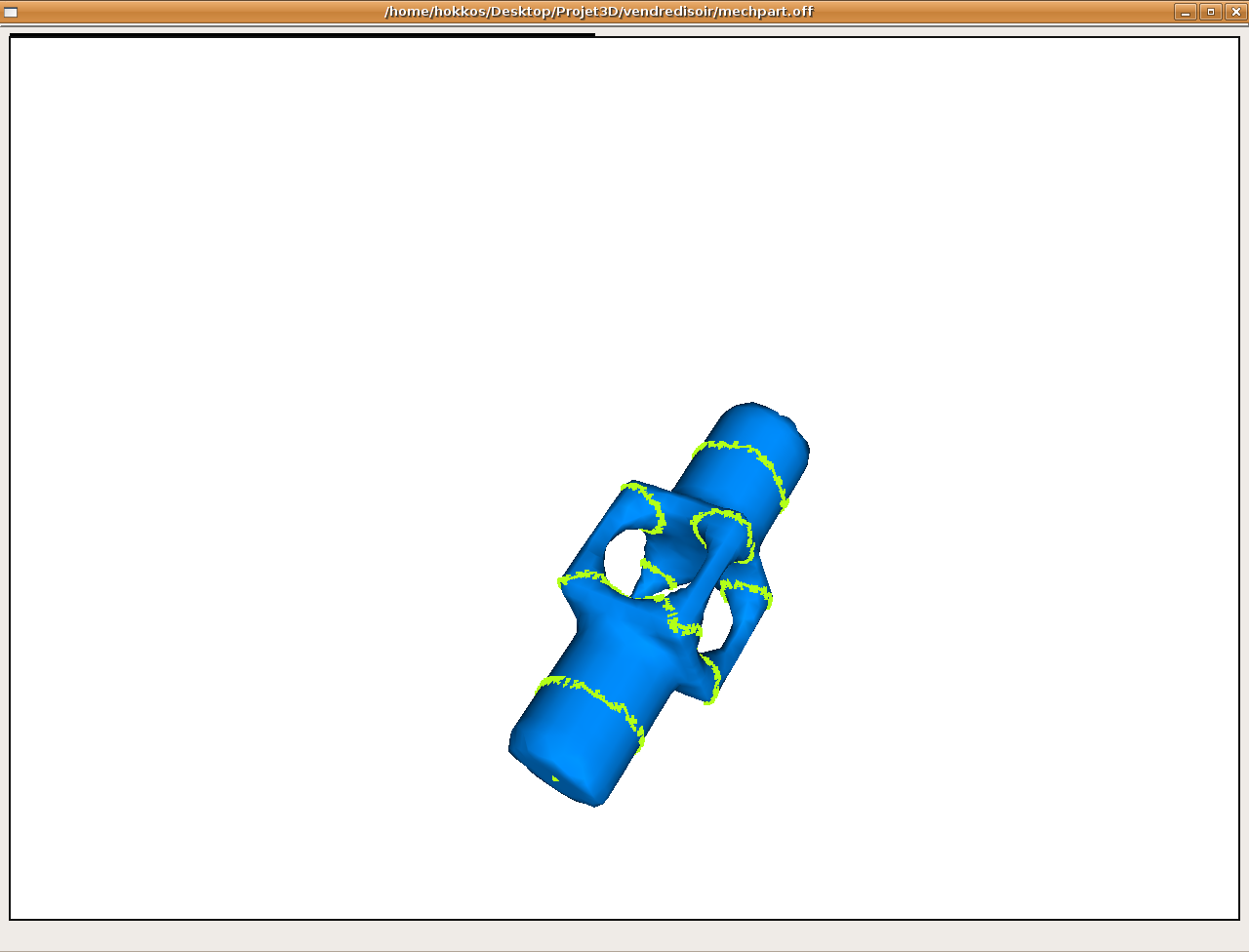
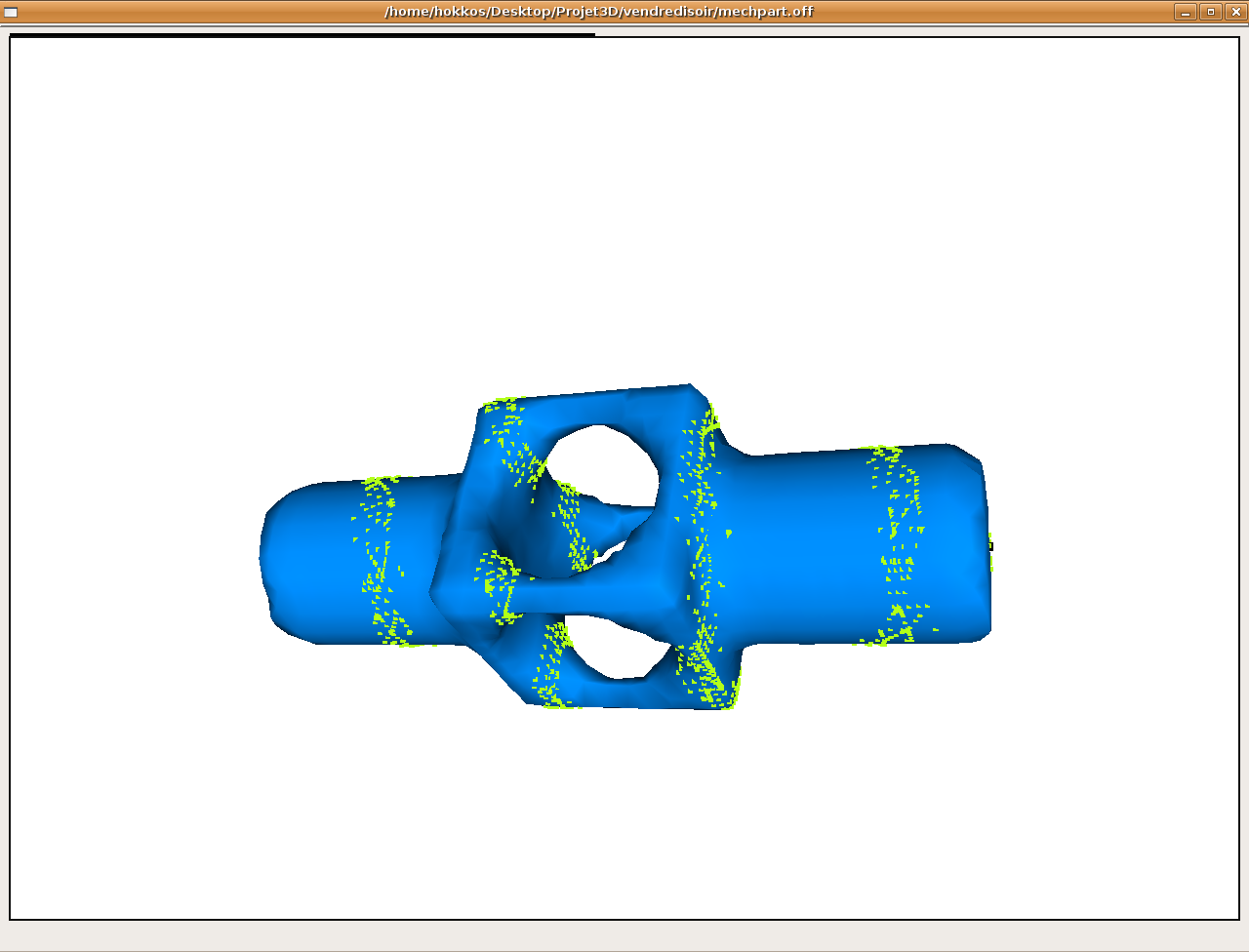
Isodistances des l'algo 1 et 3




-approximation des géodésiques par le tracé des précédents du Dijkstra:



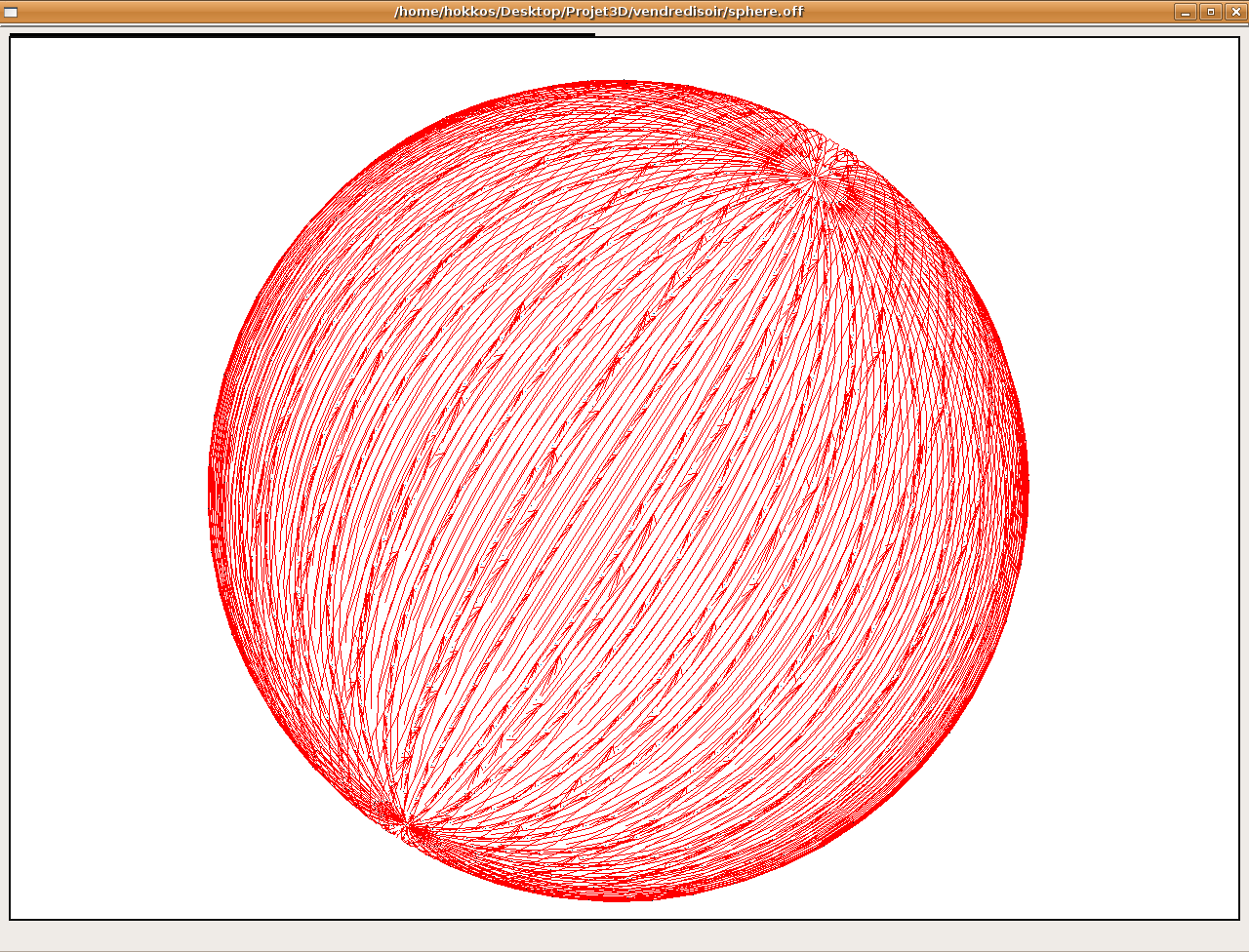
Puis nous avons fait afficher les graphes de précédents des Disjkstra, ceux-ci devraient être similaires aux géodésiques. On le constate expérimentalement sur l'algorithme 1 et dans une moindre mesure sur l'algorithme 3 (en effet dans l'algo 3 on fait l'approximation suivante : une arête égale un intervalle (au sens intervalle de l'algo 2 qui lui est normalement exacte). On obtient donc plutôt une forme d'arbre qui longe les géodésiques.

précédents pour l'algo1



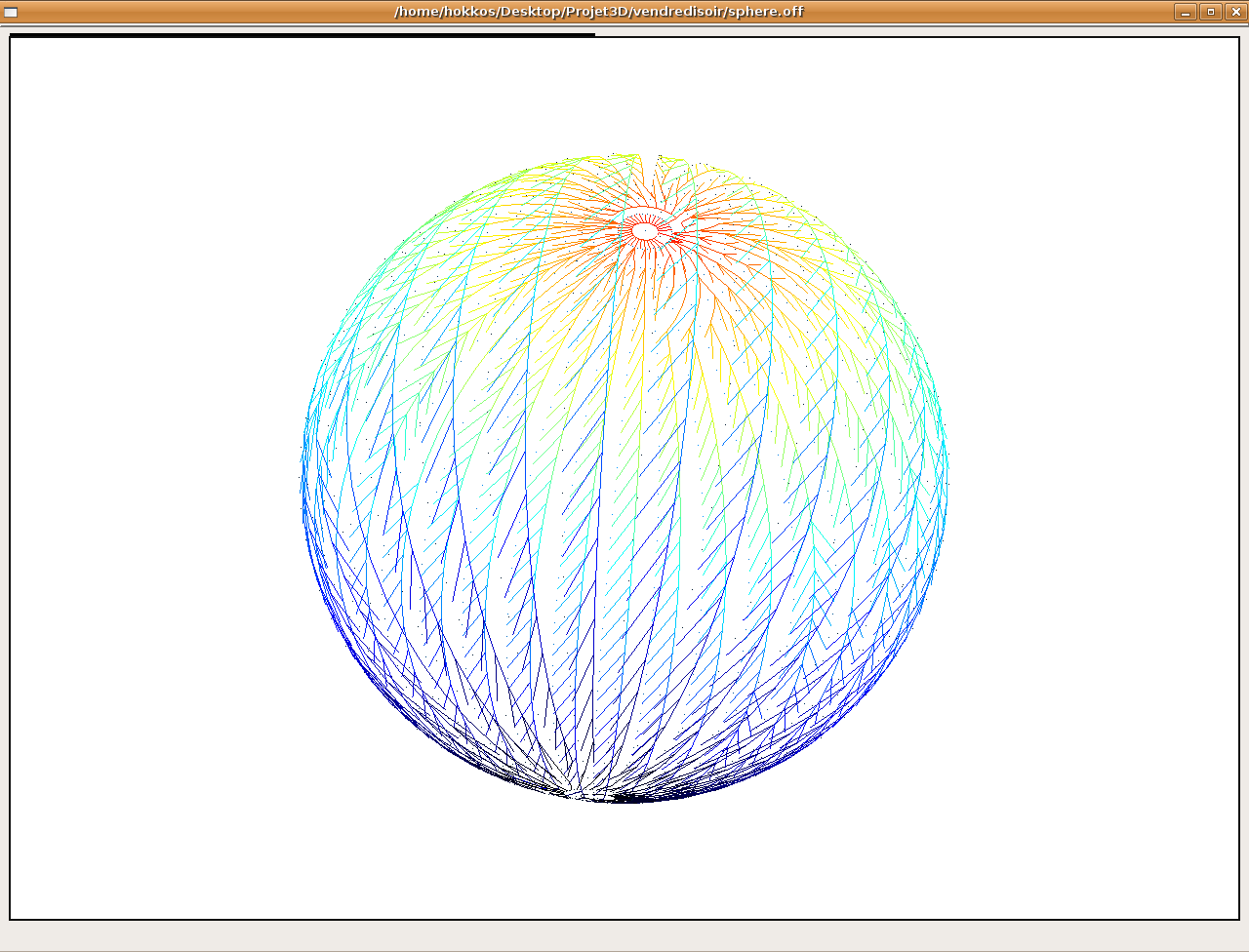
précédents pour l'algo2








Pour l'algorithme 2, on obtient des résultats très imparfaits dans ce mode d'affichage car les précédents ne sont pas bien mémorisés (ceci est du à un problème de chaînage non trivial lorsque l'on merge les nouveaux intervalles propagés avec ceux déjà présents sur l'arête. Il peut être résolu en créant une liste d'intervalles suivant sur chaque intervalle). On identifie cependant des résultats qui rappellent ceux donnés par l'algo3.




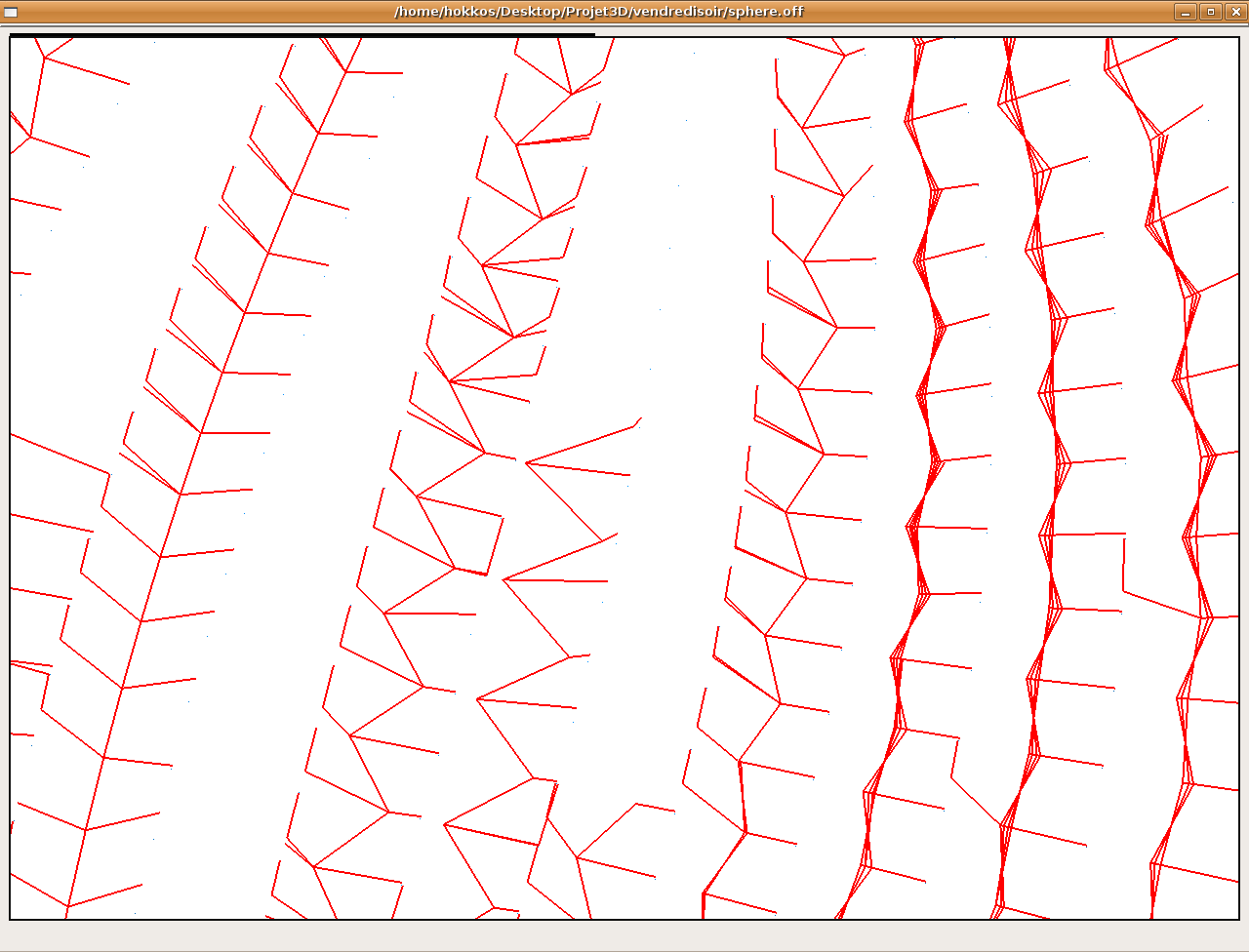
précédents pour l'algo3



-Pour le débugage...

Pour ce qui est de l'algorithme 2 nous avons implémenté un mode d'affichage pas à pas qui détaille chaque étape de propagation. Ainsi l'on a pu vérifier que la majorité des cas possibles de propagation est bien traitée (cependant il n'ont pas tous été testés exhaustivement du fait de leur nombre).






-petit test comparatif


Enfin pour avoir une idée de la précision et des différences entre les algorithmes, nous faisons afficher la distance maximale à partir du point source de la figure. Et l'on constate que l'algo3 renvoie des valeurs éloignés de l'ordre de 10% par rapport aux deux autres algorithmes qui ont eux des valeurs assez proches sur la sphère. Cependant la différence peut atteindre 10% sur des figures plus complexes comme le noeud.




Conclusion :


Ce projet nous a permis de travailler avec des outils 3D élaborés tels que CGAL et openGL. Nous avons pu apprécier les problèmes que pouvaient engendrer les erreurs numériques et quelques solutions à ces problèmes. Au niveau du travail d'équipe, cela s'est bien passé : On avait plutot des domaines de compétence un peu disjoints (CGAL; C++; géométrie/mathématiques) ce qui fait que nous avons pu nous entraider mutuellement.

Au niveau des tests sur les algorithmes, on constate finalement que l'algorithme 1 est le plus stable. Pour les 2 autres algorithmes, il est nécessaire de faire une implémentation très soignée et une « bonne » gestion de la mémoire pour éviter au maximum sa saturation.