Sujet 2 :
calcul itératif de géodésiques discrètes
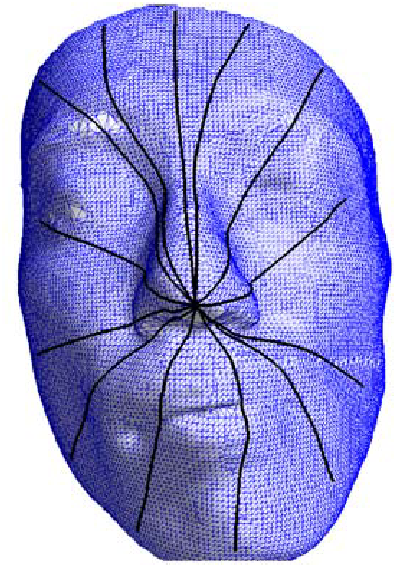
Article de référence
Computing Geodesics on Triangular Meshes, par D. Martinez, L. Velho et P. Carvalho, Computer & Graphics 2005.Cet article présente un algorithme de calcul de géodésiques, c'est-à-dire de plus courts chemins locaux (ou de manière équivalente, de plus courts chemins étant donnés un sommet et une direction de départ), entre deux sommets donnés de la surface. Pour cela, il calcule un premier chemin entre les deux sommets, selon un algorithme proposé par Sethian et Kimmel en 1995, qu'il essaie ensuite itérativement d'optimiser.
Travail demandé
- Implémenter cet algorithme et les améliorations présentées dans le papier (notamment l'utilisation du tas).
- Tester ses performances (temps de calcul, place mémoire ...) sur diverses surfaces maillées (de tailles diverses, pour des maillages uniformes et non uniformes) et en tirer des conclusions.
- Tester l'algorithme avec d'autres chemins initiaux (par exemple un chemin tracé manuellement), et en tirer des conclusions.
- Proposer des améliorations (en particulier, avez-vous des idées d'autres critères d'arrêt ? Pourrait-on adapter cet algorithme pour calculer des straightest geodesics ?).
A lire aussi
- Computing Geodesic Paths on Manifolds,
par J. Sethian et R. Kimmel, Proceedings of the National Academy of Sciences of
the USA 1995.
L'article de Sethian et Kimmel, qui vous sera nécessaire pour calculer un chemin initial. - Straightest Geodesics on Polyhedral
Surfaces, par K. Polthier et M. Schmies, Visualization and Mathematics 1998.
Pour plus d'information sur les "straightest geodesics".