Sujet 2 :
remaillage semi-régulier par approximation variationnelle
Article de référence
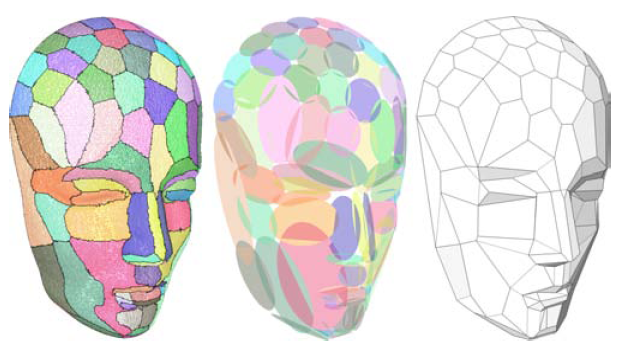
Variational Shape Approximation, par D. Cohen-Steiner, P. Alliez et M. Desbrun (un ancien de l'ENSIMAG !), SIGGRAPH 2004.Cet article explique comment définir de manière rigoureuse une approximation d'un maillage par un ensemble de "primitives" géométriques, et propose un algorithme de calcul d'une telle approximation. Il est très rigoureux d'un point de vue théorique, mais nécessite de bonnes connaissances en géométrie différentielle.
Travail demandé
- Implémenter l'algorithme d'approximation de maillage de Cohen-Steiner, Alliez et Desbrun. Tester les deux métriques proposées (L^2 et L^{2,1}).
- Améliorer cet algorithme afin qu'il soit entièrement automatique (nombre de régions, ...). Vous pouvez vous inspirer des suggestions de la section 3.5.
- Développer et implémenter un algorithme de remaillage semi-régulier à partir de l'algorithme précédent : le maillage grossier sera construit à partir de l'approximation par primitives. Vous pouvez vous inspirer de la méthode de remaillage expliquée en section 4 de l'article.
- Tester votre algorithme et en tirer des conclusions.
A lire aussi
- Least Square Quantization in PCM, par S.
Lloyd, IEEE Trans. Inform. Theory 1982.
L'algorithme de Lloyd, décrit dans cet article, est un algorithme aujourd'hui classique de partition d'un ensemble de points en k régions. Il date de 1957, mais n'avait jamais été publié et est tombé dans l'oubli jusqu'en 1982. A lire surtout pour comprendre les préoccupations des "informaticiens" il y a 50 ans ! - A Local Search Approximation
Algorithm for k-Means Clustering, par T. Kanungo, D. Mount, N. Netanyahu, C.
Piatko, R. Silverman et A. Wu, Symposium on Computational Geometry, 2002.
Une variante de l'algorithme de Lloyd. - Superfaces: Polygonal Mesh
Simplification with Bounded Error, par A.D. Kalvin et R.H. Taylor, IEEE
Computer Graphics and Applications, 1996.
Un algorithme de simplification de maillages par fusion de faces, dont vous pouvez vous inspirer pour la partie 3 du travail.