Projet Image 2009

Reconstruction interactive de maillage

Besnier Arnaud, Huard Mathieu, Luna Florian, Bouvier Vincent

Quelques fichiers

• Programme de réparation de maillages v1.0

Introduction

Le projet sur lequel nous avons travaillé cette année concerne la réparation des maillages produits par un scanner 3D. Un tel scanner procède en scannant successivement le même objet sous différents angles, après quoi ces différentes vues sont recollées automatiquement par un logiciel propriétaire(ScanStudio dans le cas du scanner que l'Inria nous a fourni). Au moment du recollement, le maillage obtenu est simplifié, et l'on obtient une entité correspondant à l'objet scanné. Outre les imperfections dûes aux algorithmes de reconstruction, l'opération est rendue complexe par la simple topologie des objets scannés, qui empêche une acquisition satisfaisante de zones critiques ou obstruées. Les différents algorithmes automatiques qui ont pu être implémentés n'ont jamais réellement résolu le problème. Ainsi, notre projet se base sur un article récent qui propose une méthode interactive, décrite un peu plus bas : Interactive Topology-Aware Surface Reconstruction, par A. Sharf, T. Lewiner, G. Shklarski, S. Toledo et D. Cohen-Or, publié à SIGGRAPH en 2007.

Prise en main du scanner

Pour des généralités sur le scanner que nous avons utilisé, on peut se référer au projet réalisé l'an dernier (cf. Bibliographie). D'un point de vue matériel, le scanner réalise des photos de bonne qualité, et de façon très automatisée. La complexité se situe plutôt au niveau logiciel, puisqu'il ne parvient que rarement à assembler les différentes vues. Il faut donc le guider en définissant des points de fusion sur plusieurs des vues, une opération qui s'avère parfois compliquée. Les différents maillages correspondant aux vues sont fusionnés automatiquement, mais il en résulte un maillage trop raffiné, et donc très lourd, bien que conforme à l'objet scanné. Enfin, mentionnons que le logiciel ScanStudio fournit un algorithme de réparation de maillage, très approximatif. Il en ressort un maillage effectivement "étanche", mais avec un niveau de détail déplorable par rapport à l'objet initial.(à suivre, image du joker).
Un exemple d'éléphant :

Algorithme de Sharf

L'algorithme à implémenter se décompose en plusieurs étapes :

• Calcul et affichage de la surface implicite relative à l'objet scanné
• Détection et affichage sur la surface de "zones faibles" où l'utilisateur pourra ajouter des contraintes
• Mise à jour de la surface implicite à partir des nouvelles contraintes

Nous avons appliqué quelques modifications et autres adaptations de l'algorithme décrit dans l'article, ceci notamment pour des contraintes de temps d'une part, de simplicité d'interaction avec l'interface d'autre part. C'est pourquoi l'on explicite ci-dessous les différentes étapes telles qu'elles sont implémentées dans notre code, en signalant les variantes majeures :

1. Calcul et affichage de la surface implicite

Le calcul de la surface résulte d'un problème de minimisation d'une fonction qui pénalise l'irrégularité de la fonction et l'éloignement aux points du maillage. Ce problème est résolu par la méthode des éléments finis. L'article utilise un maillage de l'espace à base d'octrees, qui permettent de raffiner la subdivision de l'espace au voisinage des contraintes. Nous n'avons pas eu le temps d'implémenter cette structure, et avons donc utilisé un maillage régulier sur tout l'espace occupé par l'objet scanné. Il s'agit d'un maillage tétraédrique, composé de cubes tous identiques, découpés identiquement en tétraèdres de la façon suivante :


On verra que cette décomposition a l'avantage de faciliter la reconstruction prochaine de la surface implicite.

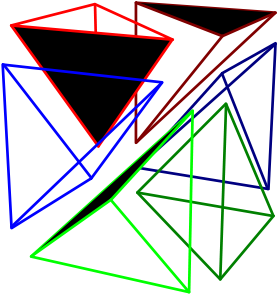
Une fois le problème d'éléments finis résolus, on a la valeur de la fonction implicite à tous les sommets du maillage tétraédrique. Pour reconstruire la surface implicite à partir de ces sommets, on utilise la méthode des "marching tetrahedra", qui utilise la même partition de l'espace que notre maillage. Il était question dans l'article de "dual marching cubes" qui eux se basaient sur la structure d'octree que nous n'avons pas utilisée.

L'algorithme est inspiré du marching cube. Il permet de reconstituer une surface à partir des valeurs d'une fonction implicite sur le maillage tétraédrique présenté. Il permet de séparer les valeurs positives des négatives. Par convention, les valeurs négatives sont à l'intérieur de la surface si elle est fermée.
x L'algorithme se programme à trois niveaux de complexité.
• Dans un premier lieu, on étudie toutes les configurations possibles sur un tétraèdre. On regarde donc si, toutes les valeurs sont de même signe, ou si une seule est différente, ou s'il y a des groupes de 2. Pour plus de précision, l'article de wikipédia réfère très bien ces configurations.
• Nous avons appliqué donc ce mini-algorithme à tous les tétraèdres composants un cube. Voici quelques configurations possibles pour un cube.
Enfin, nous avons parcouru tous les cubes du maillage. En guise de tests globaux nous avons utilisé une sphère. Pour un pas de 150, le résultat est : Le principal avantage du marching tétraèdre est qu'il est plus facile à programmer que le marching cube. En effet celui nécessite de préenregistrer 256 configurations possibles, tandis qu'ici, il n'y en a que 8. De plus, le nombre de faces générées est beaucoup plus grand et réaliste que le marching cube.
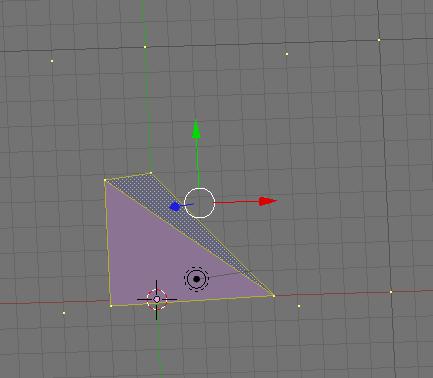
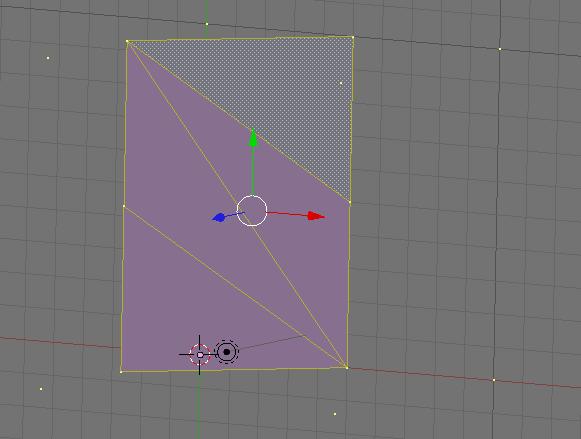
L'idéal aurait été d'appliquer un algorithme de lissage sur l'image. Mais le nombre de points générés est très grand et le lissage devient trop long. Pour cela, nous avons retirer les vertex en double. Cependant, avoir fait cela crée des arrêtes complexes car plusieurs mêmes arrêtes sont collées entre elles. Une amélioration notable peut donc ici se faire. Le principal frein a été le manque de documentation d'OpenMesh.
L'éléphant après reconstruction de surface implicite

Concernant le calcul des valeurs de la fonction implicite, de nombreuses optimisations ont été faites. Elles étaient indispensables au regard du temps de calcul extrêmement long même sur un maillage assez grossier.
Les matrices à manipuler possèdant plusieurs milliards d'éléments, nous avons eut recourt à deux librairies différentes :
• CHOLMOD permet l'utilisation de matrices creuses. Nos matrices étant principalement remplies de 0, cette librairie nous offre un temps de calcul réduit.
  De plus, CHOLMOD permet l'utilisation de la méthode de CHOLESKY de manière efficace pour la résolution d'un problème de type AX=B.
• TNT/JAMA qui sont des librairies moins puissantes que CHOLMOD mais qui offrent l'avantage de permettre la multiplication et la somme sur des matrices denses.
2. Détection et affichage des zones faibles

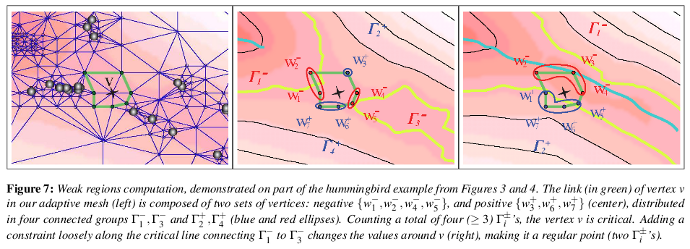
L'ensemble des points du maillage sont parcourus. Pour chacun de ces points, nous créons un circulateur sur l'ensemble des points avec lequel il est lié. Pour déterminer si un point est critique, on partitionne l'ensemble des points wi adjacents au point courant v en deux ensembles de points (les positifs et les négatifs). Les points positifs sont tels que u(wi) > u(v) et les points négatifs tels que u(wi) >= u(v). Chaque ensemble de points (les wi positifs ou négatifs liés par des arêtes) est compté. Si le nombre total de de groupes connectés est de 1 ou supérieur ou égale à 3, le point est critique et définit une zone topologiquement faible. L'illustration ci-dessous extraite du papier de recherche étudié nous montre un exemple en 2D qui à l'avantage d'être assez explicite :



3. Mise à jour de la surface implicite

L'interface de notre logiciel

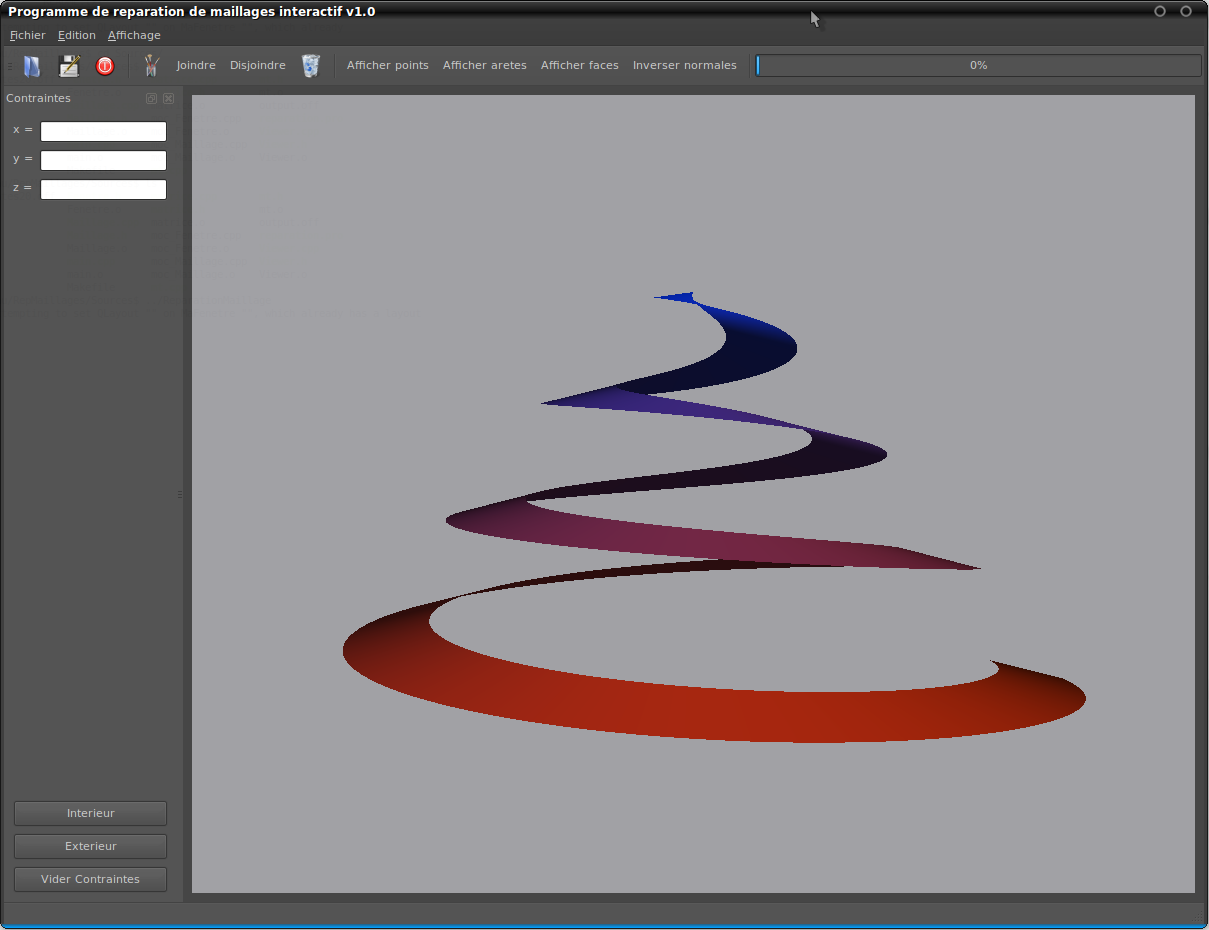
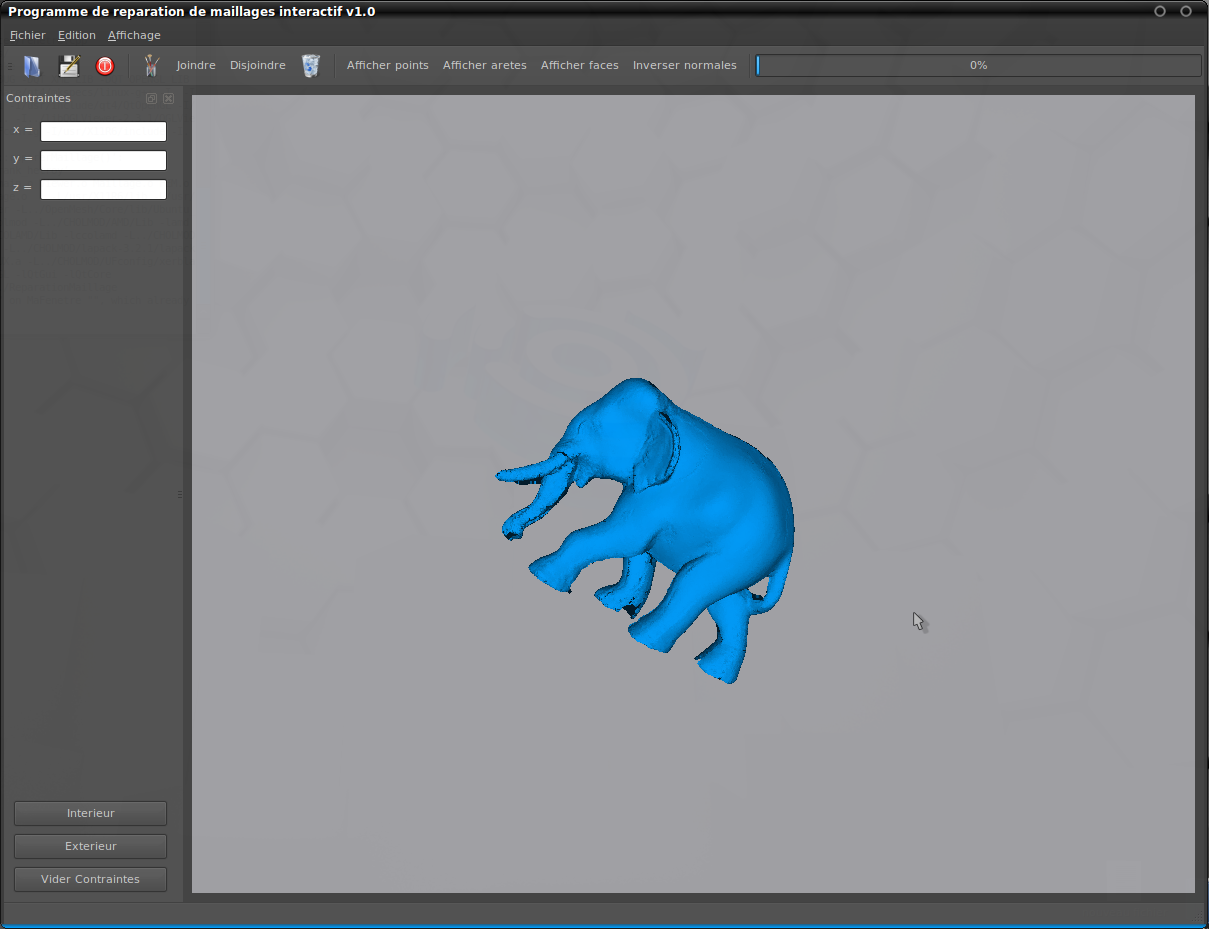
Nous avons choisi de créer notre interface à partir de zéro suites aux difficultées que nous avons rencontrées pour compiler l'interface "de base" livrée en début de projet. Cette interface basée sur Qt4 intègre un viewer construit avec la librairie QGLViewer. Cette interface peut effectuer diverses opérations accessibles sur la barre des tâches :

• Ouvrir un fichier .obj ou .off (également accessible par Ctrl+O ou Fichier->Ouvrir)
• Enregister un maillage au format .obj ou .off (également accessible par Ctrl+S ou Fichier->Enregistrer)
• Supprimer le maillage visible dans le viewer (également accessible par Ctrl+D ou Edition->Supprimer)
• Changer le mode d'affichage du maillage (points, arêtes ou faces) (également accessible dans le menu Affichage)
• Inverser le sens des normales du maillage (également accessible dans le menu Affichage)
• Lancer la réparation du maillage du maillage(également accessible par Ctrl+R ou Edition->Reparer)
• Définir si la courbe dessinée sur le plan courant (en vert) sera une courbe de jonction ou de disjonction (également accessible dans le menu Edition)
• Quitter le programme (également accessible par Ctrl+Q ou Fichier->Quitter)
D'autres opérations ne sont pas accessibles depuis la barre des tâches :
• Sélectionner un des plans qui représente une zone topologiquement faibles (Shift+clic droit)
• Dessiner une courbe sur chacun des plans représentants les zones topologiquement faibles (Shift+clic droit sur le plan selectionné pour y ajouter un point)

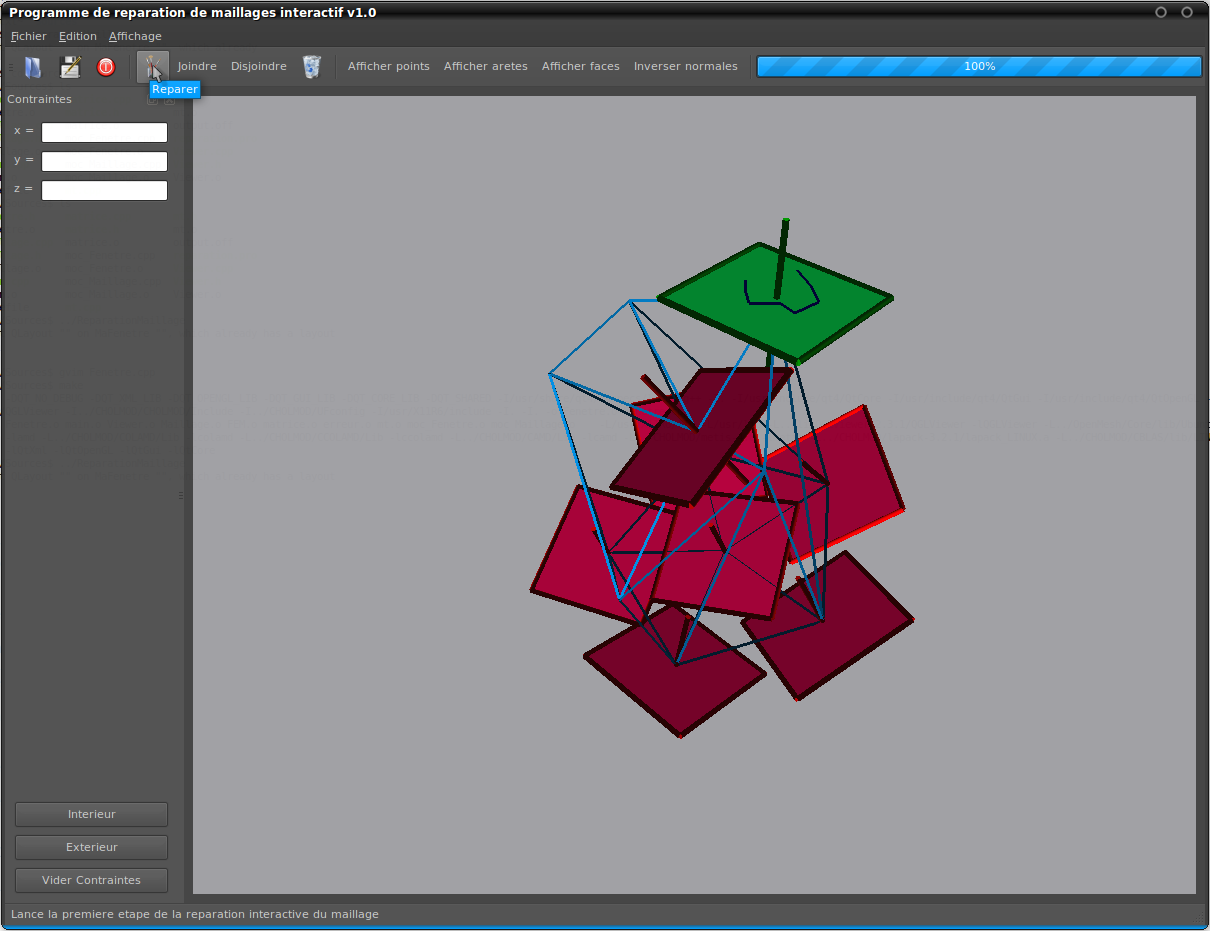
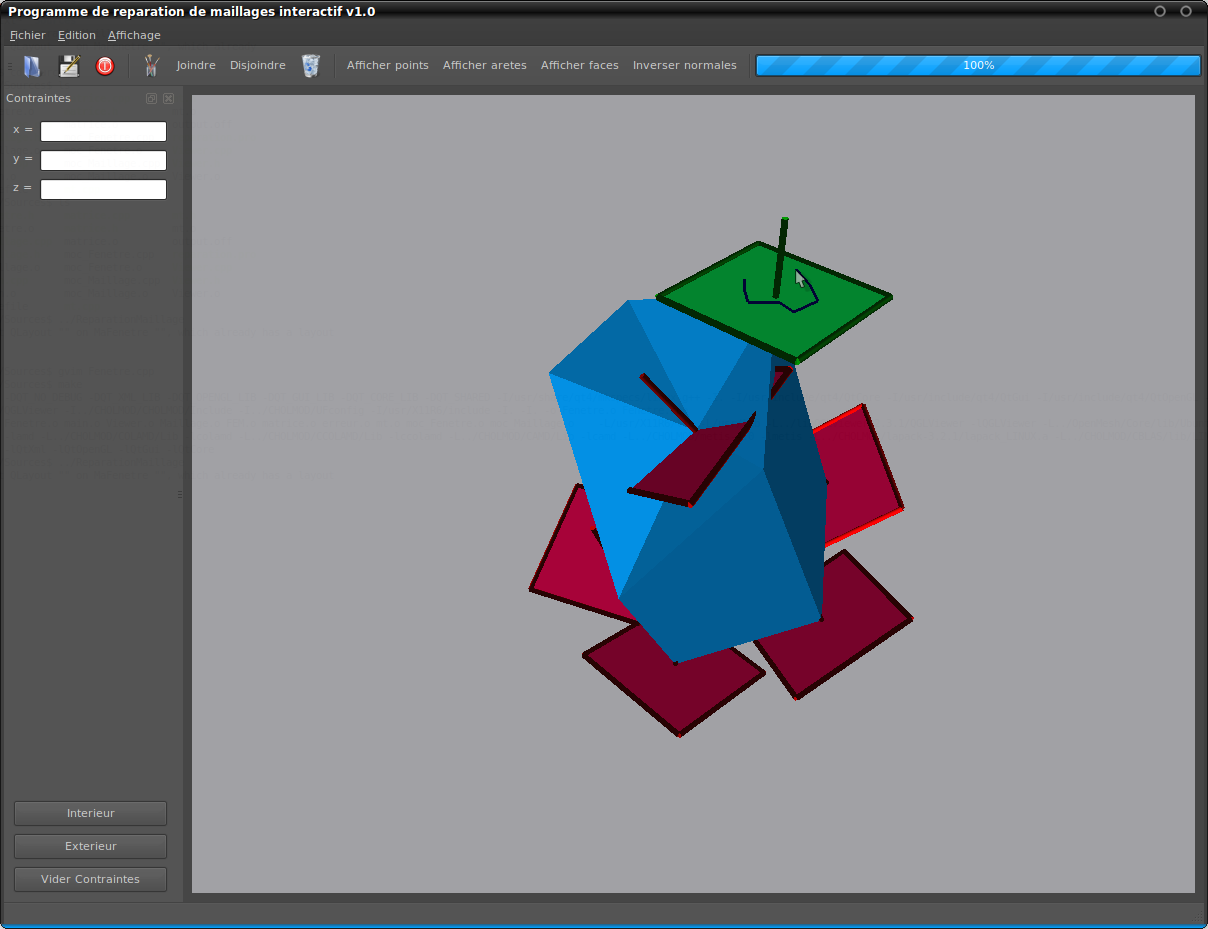
A noter que si vous voulez ouvrir un fichier, son chemin absolu ne devra dépasser les 60 caractères. Dans le cas contraire un message d'erreur apparaitra au niveau de l'interface et aucun fichier ne sera ouvert. Nous ne comprennons pas pourquoi mais si le chemin absolu a plus de 60 ou 62 caractères, le programme ajoute un charactère à la fin du nom de fichier, celui-ci n'est alors pas trouvé dans l'arborescence.

Bilan du projet, tests et résultats

Nous n'étions pas trop de quatre pour ce projet de réparation de maillages ! L'installation des multiples bibliothèques, la réalisation d'une interface graphique, l'implémentation de concepts mathématiques poussés et une méthodologie de programmation rigoureuse ont été tant de compétences nécessaires pour arriver à un résultat correct. L'algorithme de Sharf n'a été que partiellement implémenté, et ne fonctionne qu'avec de faibles résolutions, mais les surfaces implicites sont reconstruites avec succès. L'interface graphique, même si sa gestion des zones faibles n'est pas exploitée par nos travaux, est complète et fonctionnelle.
Ainsi, le bilan est plutôt mitigé : le projet, bien que passionnant sous bien des aspects, nous a paru très ambitieux, et il est regrettable que nous ayons perdu du temps sur des aspects plus "futiles" comme l'installation de bibliothèques, même si la maîtrise de ces bibliothèques s'avérera certainement utile pour nous par la suite. C'est la raison pour laquelle nous avons écrit quelques tutoriaux pour les projets des années à venir.

Problèmes à résoudre, optimisations possibles

• Problème de dichotomie à 2.05 pour la recherche du cube contenant un point du maillage.
• Lors de la recherche du tétraèdre contenant un point du mesh donné, lorsque le point se trouve sur une face ou une arrête d'un tétraèdre, il faudrait le détecter pour pouvoir interpoler suivant 2 ou 3 points.

Tutoriaux d'installation des librairies

La première étape du projet, et l'une des plus longues, fut l'installation des différentes librairies permettant la gestion et l'affichage de maillage. Devant les difficultés rencontrées et notre altruisme évident, nous offrons aux génériations futures ou passées quelques tutoriaux d'installation pour les principales librairies utilisées lors de notre projet.

• Qt4
  Permet la création d'interfaces (à l'avantage d'être multi-plateforme).
• libQGLViewer
  Permet la création rapide d'un viewer pour visualiser des maillages.
• OpenMesh
  Permet la gestion du maillage.
• CHOLMOD
  Librairie de gestion de matrices très efficace permettant notamment l'utilisation de "sparse" matrice pour le cas d'une matrice présentant beaucoup de 0.

Explications de l'installation de l'ensemble des librairies et du programme de réparation de maillage