Sujet 1 :
réparation interactive de maillages
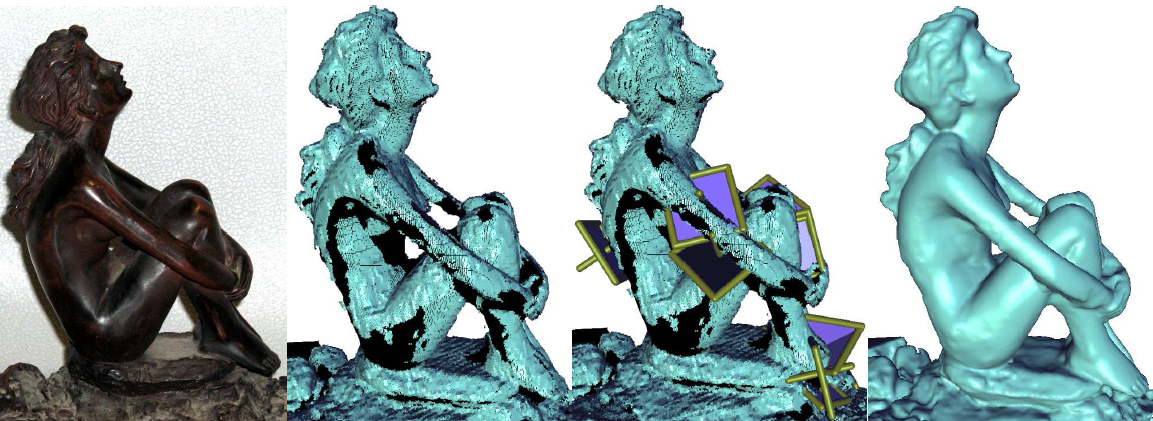
De gauche à droite : une statuette, maillage construit par le scanner, détection de zones à réparer, maillage final (images Andrei Sharf et al.).
Cadre du projet
Encadrant : Franck HétroyNombre d'étudiants : 3
Lieu : le scanner est disponible à l'Atelier de Réalité Virtuelle de l'Ensimag, sur le site de Montbonnot. Le projet aura donc lieu pour partie à cet endroit (pour venir à Montbonnot, voir le site de l'Ensimag), et pour partie en salle D200 à l'Ensimag.
Prérequis : aucun, hormis les cours obligatoires d'algorithmique et de programmation de 1A et 2A. Cependant, avoir suivi le cours de modélisation géométrique au premier semestre serait un plus.
Contexte
L'Ensimag a acquis à l'automne 2007 un scanner 3D de bureau. Ce scanner permet de convertir des modèles 3D réels en maillages virtuels, qui peuvent ensuite être visualisés et manipulés pour des applications très diverses :- effets spéciaux pour le cinéma ;
- prototypage virtuel pour l'industrie (automobile, aéronautique, ...) ;
- restauration virtuelle d'oeuvres d'art ;
- analyse scientifique d'échantillons géologiques ;
- etc.
Travail demandé
- Prendre en main le scanner et son logiciel.
- Scanner différents modèles de votre choix.
- Implémenter/adapter l'algorithme de Sharf et al. décrit ci-dessous.
- Tester cet algorithme sur les modèles scannés, et faire un bilan critique.
- Eventuellement, proposer des pistes d'amélioration à l'algorithme.
Article de référence
Interactive Topology-Aware Surface Reconstruction, par A. Sharf, T. Lewiner, G. Shklarski, S. Toledo et D. Cohen-Or, SIGGRAPH 2007.Cet article propose un algorithme de reconstruction de maillage à partir d'un ensemble de points (il ne tient donc pas compte du maillage défectueux construit par le logiciel fourni avec le scanner). L'algorithme fonctionne en deux étapes :
- il calcule une fonction continue implicite tri-dimensionnelle F telle que l'ensemble de niveau F0 = { x, F(x) = 0 } est une approximation des points de départ ;
- F est ensuite explicitée, comme solution d'un problème de minimisation, et la surface F0 est donc explicitement construite.
Liens utiles
- Ma page générale sur les projets image proposés en 2009. Quelques détails techniques et des précisions sur ce que j'attends de vous.
- Le site du fabricant du scanner. Pas mal de vidéos de démonstration.
- La page d'Andrei Sharf sur ce projet. Avec notamment une vidéo et les transparents de sa présentation à SIGGRAPH.
- La bibliothèque OpenMesh, une bibliothèque C++ pour la gestion des maillages (statiques).
- La page de Tamy Boubekeur. Plein d'infos utiles sur la construction de modèles 3D à partir de scans.