| The Java 3D API Specification |
|
| The Java 3D API Specification |
|
A P P E N D I X  E E |
|
Equations |
· Multiplication Function operator for sound equations;
Dot product for all other equations
E.1
The ideal fog equation isFog Equations
The fog coefficient, f, is computed differently for linear and exponential fog. The equation for linear fog is
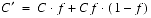
(Eq. E.1)
The equation for exponential fog is
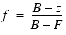
(Eq. E.2)
The parameters used in the fog equations are
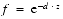
(Eq. E.3)
1. An implementation may approximate per-pixel fog by calculating the correct fogged color at each vertex and then linearly interpolating this color across the primitive.
2. An implementation may approximate exponential fog using linear fog by computing values of F and B that cause the resulting linear fog ramp to most closely match the effect of the specified exponential fog function.
3. An implementation will ideally perform the fog calculations in eye coordinates, which is an affine space. However, an implementation may approximate this by performing the fog calculations in a perspective space (such as device coordinates). As with other approximations, the implementation should match the specified function as closely as possible.
E.2
The ideal lighting equations areLighting Equations
Note: If (LiN)
0, then diffi and speci are set to 0.
Note: For directional lights, atteni is set to 1.
Note: If the vertex is outside the spot light cone, as defined by the cutoff angle, spoti is set to 0. For directional and point lights, spoti is set to 1.
This is a subset of OpenGL in that the Java 3D ambient and directional lights are not attenuated and only ambient lights contribute to ambient lighting.The parameters used in the lighting equation are
E = Eye vector Ma = Material ambient color Md = Material diffuse color Me = Material emissive color Ms = Material specular color N = Vertex normal shin = Material shininess
1. An implementation may approximate the specular function using a different power function that produces a similar specular highlight. For example, the PHIGS+ lighting model specifies that the reflection vector (the light vector reflected about the vertex normal) is dotted with the eye vector and that this dot product is raised to the specular power. An implementation that uses such a model should map the shininess into an exponent that most closely matches the effect produced by the ideal equation.
2. Implementations that do not have a separate ambient and diffuse color may fall back to using an ambient intensity as a percentage of the diffuse color. This ambient intensity should be calculated using the following NTSC luminance equation:
I = 0.30 · Red + 0.59 · Green + 0.11 · Blue (Eq. E.9) E.3
There are different sets of sound equations, depending on whether the application uses headphones or speakers.Sound Equations
E.3.1
For each sound source, Java 3D calculates a separate left and right output signal. Each left and right sound image includes differences in the interaural intensity and an interaural delay. The calculation results are a set of direct and indirect (delayed) sound signals mixed together before being sent to the audio playback system's left and right transducers.Headphone Playback Equations
E.3.1.1
For each PointSound and ConeSound source, the left and right output signals are delayed based on the location of the sound and the orientation of the listener's head. The time difference between these two signals is called the interaural time difference (ITD). The time delay of a particular sound reaching an ear is affected by the arc the sound must travel around the listener's head. Java 3D uses an approximation of the ITD using a spherical head model. The interaural path difference is calculated based on the following cases:Interaural Time Difference (Delay) 1. The signal from the sound source to only one of the ears is direct. The ear farther from the sound is shadowed by the listener's head (
); see Figure E-1.
- where
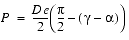
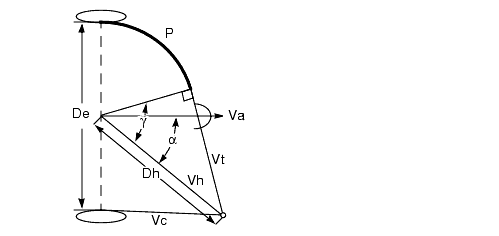
Figure E-1
Signal to Only One Ear Is Direct
2. The signals from the sound source reach both ears by indirect paths around the head (
); see Figure E-2.
The time from the sound source to the closer ear is
- where
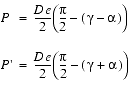
, and the time from the sound source to the farther ear is
, where S is the current AuralAttribute region's speed of sound.
If the sound is closer to the left ear, then
If the sound is closer to the right ear, then
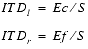
(Eq. E.12)
Figure E-2
Signals to Both Ears Are Indirect
The parameters used in the ITD equations are as follows:
E.3.1.2
For each active and playing Point and ConeSound source, i, separate calculations for the left and right signal (based on which ear is closer to and which is farther from the source) are combined with nonspatialized BackgroundSound to create a stereo sound image. Each of the following equation is calculated separately for the left and right ear.Interaural Intensity (Gain) Difference
Note: For BackgroundSound sources, ITDi is an identity function so there is no delay applied to the sample for these sources.
Note: For BackgroundSound sources Gdi = Gai = 1.0. For PointSound sources Gai = 1.0.
Note: For BackgroundSound sources, Fdi and Fai are identity functions. For PointSound sources, Fai is an identity function.
If the sound source is on the right side of the head, Ec is used for left G and F calculations, and Ef is used for right. Conversely, if the Sound source is on the left side of the head, Ef is used for left calculations, and Ec is used for right.
Attenuation
For sound sources with a single distanceGain array defined, the intersection points of Vh (the vector from the sound source position through the listener's position) and the spheres (defined by the distanceGain array) are used to find the index k where dkL
dk+1. See Figure E-3.
For ConeSound sources with two distanceGain arrays defined, the intersection points of Vh and the ellipsi (defined by both the front and back
distanceGainarrays) closest to the listener's position are used to determine the index k. See Figure E-4.The equation for the distance gain is
Figure E-3
ConeSound with a Single Distance Gain Attenuation Array
Figure E-4
ConeSound with Two Distance Attenuation Arrays
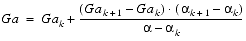
(Eq. E.18) Filtering
Similarly, the equations for calculating the AuralAttributes distance filter and the ConeSound angular attenuation frequency cutoff filter are
An N-pole lowpass filter may be used to perform the simple angular and distance filtering defined in this version of Java 3D. These simple lowpass filters are meant only as an approximation for full, FIR filters (to be added in some future version of Java 3D).
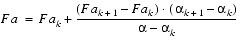
(Eq. E.20) 1. If more than one lowpass filter is to be applied to the sound source (for example, both an angular filter and a distance filter are applied to a ConeSound source), it is necessary only to use a single filter, specifically the one that has the lowest cutoff frequency.
The parameters used in the interaural intensity difference (IID) equations are as follows:2. There is no requirement to support anything higher than very simple two-pole filtering. Any type of multipole lowpass filter can be used. If higher N-pole or compound filtering is available on the device on which sound rendering is being performed, use of these is encouraged, but not required.
E.3.1.3
Between two snapshots of the head and the sound source positions some delta time apart, the distance between the head and source is compared. If there has been no change in the distance between the head and the sound source over this delta time, the Doppler effect equation isDoppler Effect Equations
If there has been a change in the distance between the head and the sound, the Doppler effect equation is
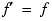
(Eq. E.21)
When the head and sound are moving toward each other (the velocity ratio is greater than 1.0), the velocity ratio equation is
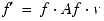
(Eq. E.22)
When the head and sound are moving away from each other (the velocity ratio is less than 1.0), the velocity ratio equation is
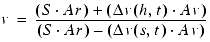
(Eq. E.23)
The parameters used in the Doppler effect equations are as follows:
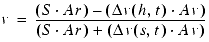
(Eq. E.24)
Note: If the adjusted velocity of the head or the adjusted velocity of the sound is greater than the adjusted speed of sound,is undefined.
E.3.1.4
The overall reverberant sounds, used to give the impression of the aural space in which the active/enabled source sources are playing, is added to the stereo sound image output from equation E.14.Reverberation Equations
Reverberation for each sound is approximated in the following:
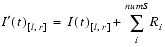
(Eq. E.25)
Note that the reverberation calculation outputs the same image to both left and right output signals (thus there is a single monaural calculation for each sound reverberated). Correct first-order (early) reflections, based on the location of the sound source, the listener, and the active AuralAttribute's bounds, are not required for this version of Java 3D. Approximations based on the reverberation delay time, either suppled by the application or calculated as the average delay time within the selected AuralAttribute's application region, will be used.
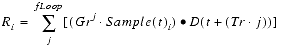
(Eq. E.26) 1. Reducing the number of feedback loops repeated while still maintaining the overall impression of the environment. For example, if -10 dB were used as the drop in gain for every doubling of distance, a scale factor of 0.015625 could be used as the effective zero amplitude, which can be reached in only 15 loop iterations (rather than the 25 needed to reach 0.000976).
The parameters used in the reverberation equations are as follows:2. Using preprogrammed "room" reverberation algorithms that allow selection of a fixed set of "reverberation types" (for example, large hall, small living room), which have implied reflection coefficients, delay times, and feedback loop durations.
E.3.2
Different speaker playback equations are used depending on whether the system uses monaural or stereo speakers.Speaker Playback Equations
E.3.2.1
The equations for headphone playback need only be modified to output a single signal, rather than two signals for left and right transducers. Although there is only one speaker, distance and filter attenuation, Doppler effect, elevation, and front and back cues can be distinguished by the listener and should be included in the sound image generated.Monaural Speaker Output
E.3.2.2
In a two-speaker playback system, the signal from one speaker is actually heard by both ears, and this affects the spectral balance and interaural intensity and time differences heard by each of the listener's ears. Crosstalk cancellation must be performed on the right and left signal to compensate for the delayed attenuated signal heard by the ear opposite the speaker. Thus a delayed attenuated signal for each of the stereo signals must be added to the output from the equations for headphone playback.Stereo Speaker Output
The parameters used in the crosstalk equations, expanding on the terms used for the equations for headphone playback, are as follows:
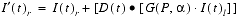
(Eq. E.28)
E.4
Texture mapping can be divided into two steps. The first step takes the transformed s and t (and possibly r) texture coordinates, the current texture image, and the texture filter parameters and computes a texture color based on looking up the texture coordinates in the texture map. The second step applies the computed texture color to the incoming pixel color using the specified texture mode function.Texture Mapping Equations
E.4.1
The texture lookup stage maps a texture image onto a geometric polygonal primitive. The most common method for doing this is to reverse map the s and t coordinates from the primitive back onto the texture image, then filter and resample the image. In the simplest case, a point in s, t space is transformed into a u, v address in the texture image space (Eq. E.29), then this address is used to look up the nearest texel value in the image. This method, used when the selected texture filter function isTexture Lookup BASE_LEVEL_POINT, is called nearest-neighbor sampling or point sampling.
If the texture boundary mode is
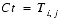
(Eq. E.31) REPEAT, then only the fractional bits of s and t are used, ensuring that both s and t are less than 1.The parameters in the point-sampled texture lookup equations are as follows:
If the selected filter function is
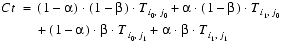
(Eq. E.34) MULTI_LEVEL_POINTorMULTI_LEVEL_LINEAR, the texture image needs to be sampled at multiple levels of detail. If multiple levels of detail are needed and the texture object defines only the base level texture image, Java 3D will compute multiple levels of detail as needed.1. If the texture boundary mode is
CLAMP, an implementation may use either the closest boundary pixel or the constant boundary color attribute for those values of s or t that are outside the range [0, 1].2. An implementation can choose a technique other than mipmapping to perform the filtering of the texture image when the texture minification filter is
MULTI_LEVEL_POINTorMULTI_LEVEL_LINEAR.3. If mipmapping is chosen by an implementation as the method for filtering, it may approximate trilinear filtering with another filtering technique. For example, an OpenGL implementation may choose to use
LINEAR_MIPMAP_NEARESTorNEAREST_MIPMAP_LINEARin place ofLINEAR_MIPMAP_LINEAR.
E.4.2
Once a texture color has been computed, this color is applied to the incoming pixel color. If lighting is enabled, only the emissive, ambient, and diffuse components of the incoming pixel color are modified. The specular component is added into the modified pixel color after texture application.Texture Application
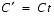
(Eq. E.35) MODULATE Texture Mode
Note that the texture format must be either
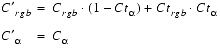
(Eq. E.37) RGBorRGBA.
Note that if the texture format is
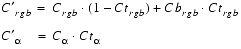
(Eq. E.38) INTENSITY, alpha is computed identically to red, green, and blue:
The parameters used in the texture mapping equations are as follows:
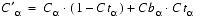
(Eq. E.39)
C = Color of the pixel being texture mapped (if lighting is enabled, then this does not include the specular component) Ct = Texture color Cb = Blend color
If there is no alpha channel in the texture, a value of 1 is used for Ct
in
BLENDandDECALmodes.
- INTENSITY: All four channels of the pixel color are modified. The intensity value is used for each of Ctr, Ctg, Ctb, and Ct
in the texture application equations, and the alpha channel is treated as an ordinary color channel-the equation for C´rbg is also used for C´
.
- LUMINANCE: Only the red, green, and blue channels of the pixel color are modified. The luminance value is used for each of Ctr, Ctg, and Ctb in the texture application equations. The alpha channel of the pixel color is unmodified.
- ALPHA: Only the alpha channel of the pixel color is modified. The red, green, and blue channels are unmodified.
- LUMINANCE_ALPHA: All four channels of the pixel color are modified. The luminance value is used for each of Ctr, Ctg, and Ctb in the texture application equations, and the alpha value is used for Ct
.
- RGB: Only the red, green, and blue channels of the pixel color are modified. The alpha channel of the pixel color is unmodified.
- RGBA: All four channels of the pixel color are modified.
Fallbacks and Approximations
An implementation may apply the texture to all components of the lit color, rather than separating out the specular component. Conversely, an implementation may separate out the emissive and ambient components in addition to the specular component, potentially applying the texture to the diffuse component only.
| The Java 3D API Specification |
|