|
François Faure
On crée une image en affectant une valeur à chacune des cases de la grille. Ces valeurs peuvent provenir directement d'un appareil à numériser (scanner) ou être calculées par un programme. Une image complexe se décompose généralement en primitives graphiques (segments de droites, arcs de cercle ou d'ellipses, polygones vides ou remplis, bitmaps, ...) qui sont tracées dans un certain ordre. Si un point fait partie de plusieurs primitives, sa valeur finale est le résultat d'une combinaison des valeurs associées à chacune d'elles. Ces combinaisons peuvent être plus ou moins complexes (opérateurs logiques, combinaisons linéaires, valeur maxi, dernière valeur spécifiée...) et le résultat peut dépendre de l'ordre dans lequel les primitives ont été tracées.
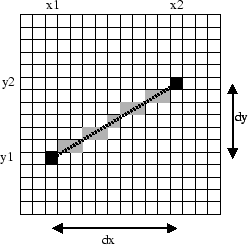
Si la pente de la droite est inférieure à ![]() , alors nous devons allumer un et un seul pixel par colonne entre
, alors nous devons allumer un et un seul pixel par colonne entre ![]() et
et ![]() . Notez que ce n'est pas le cas pour les lignes. Nous pourrions donc écrire le programme suivant:
. Notez que ce n'est pas le cas pour les lignes. Nous pourrions donc écrire le programme suivant:
Calcul par l'équation de droite ![]()
dy = y2-y1;
dx = x2-x1;
m = dy/dx;
b = y1-m*x1;
for (x=x1; x<=x2; x++) {
y=m*x+b;
plot(x,round(y));
}
Voyons maintenant les améliorations successives aboutissant à un programme optimisé. En particulier, on désire éviter les calculs en virgule flottante pour ne traiter que des entiers.
Calcul de ![]() par incrément
par incrément
dy = y2-y1;
dx = x2-x1;
m = dy/dx;
y = y1; /* <------------ */
for (x=x1; x<=x2; x++) {
plot(x,round(y));
y=y+m; /* <------------ */
}
Simplification de l'arrondi
dy = y2-y1;
dx = x2-x1;
m = dy/dx;
y = y1;
f = 0; /* <------------ */
for (x=x1; x<=x2; x++) {
plot(x,y);
f=f+m; /* <------------ */
if (f>0.5) { /* <------------ */
y = y+1;
f = f-1; /* <------------ */
}
}
Suppression de la division par dx
dy = y2-y1;
dx = x2-x1;
y = y1;
f = 0;
for (x=x1; x<=x2; x++) {
f=f+dy; /* <------------ */
plot(x,y);
if (f>(dx/2)) { /* <------------ */
y = y+1;
f = f-dx; /* <------------ */
}
}
Suppression de la division par 2
dy = y2-y1;
dx = x2-x1;
y = y1;
f = 0;
for (x=x1; x<=x2; x++) {
plot(x,y);
f=f+2*dy; /* <------------ */
if (f>dx) { /* <------------ */
y = y+1;
f = f-2*dx; /* <------------ */
}
}
Tester le signe au lieu de comparer
dy = y2-y1;
dx = x2-x1;
y = y1;
f = -dx; /* <------------ */
for (x=x1; x<=x2; x++){
plot(x,y);
f=f+2*dy;
if (f>0) /* <------------ */
y = y+1;
f = f-2*dx;
}
}
Ne modifier f qu'une seule fois par passage dans la boucle
dy = y2-y1;
dx = x2-x1;
y = y1;
f = -dx;
for (x=x1; x<=x2; x++) {
plot(x,y);
if (f>0) {
y = y+1;
f = f + 2*(dy-dx); /* <------------ */
}
else
f = f + 2*dy;
}
Précalculer des valeurs
dy = y2-y1;
dx = x2-x1;
y = y1;
f = -dx;
incrE = 2*dy; /* <------------ */
incrNE = 2*(dy-dx); /* <------------ */
for (x=x1; x<=x2; x++) {
plot(x,y);
if (f>0) {
y = y+1;
f = f + incrNE; /* <------------ */
}
else
f = f + incrE; /* <------------ */
}
Nous arrivons enfin à l'algorithme dit de Bresenham:
Sortir les bornes de la boucle
dy = y2-y1;
dx = x2-x1;
y = y1;
f = 2*dy-dx;
incrE = 2*dy;
incrNE = 2*(dy-dx);
plot(x1,y1); /* <------------ */
for (x=x1+1; x<x2; x++) { /* <------------ */
if (f>0) {
y = y+1;
f = f + incrNE;
}
else
f = f + incrE;
plot(x,y);
}
plot(x2,y2); /* <------------ */
Ce programme fonctionne pour les cas où ![]() et
et ![]() . Il est aisément adaptable aux autres cas en changeant des signes ou en permutant les rôles de x et y. Des algorithmes similaires existent pour tracer des arcs d'ellipses.
. Il est aisément adaptable aux autres cas en changeant des signes ou en permutant les rôles de x et y. Des algorithmes similaires existent pour tracer des arcs d'ellipses.
for( x=x1; x<=x2; ++x )
for( y=y1; y<=y2; ++y )
plot(x,y);
En OpenGL, on peut utiliser des points comme primitives fondamentales, en spécifiant un des modes de tracé présentés sur la figure ![]() .
.
Le mode de coloriage est spécifié par glShadeModel(GL_FLAT) pour la couleur uniforme et glShadeModel(GL_SMOOTH) pour la couleur interpolée (mode activé par défaut).