|
Ce troisième volet s'inscrit directement dans la continuité du
second, et il sera le même que vous utilisiez glut ou non. Nous allons
étudier les primitives et les matrices en nous appuyant sur le tutorial
précédent. Reprenez donc le projet que nous avions commencé,
et qui affichait un magnifique triangle blanc.
Bon, on va commencer par le dessin en OpenGL. Pour dessiner, c'est hyper simple,
et on peut faire n'importe quoi. Comme vous le savez sûrement si vous
avez légèrement touché à la 3D, TOUS les objet sont
en fait une association d'élements de base : ce sont des faces orgranisées
dans un certain ordre dans l'espace, qui représentent l'objet. Chaque
face peut être déconposée en une série de facettes
triangulaires.
| Ainsi, un rectangle est en fait constitué de deux triangles
consécutifs : |
 |
Ces triangles sont eux-même composés de 3 cotés, ou 3 lignes,
et de 3 points (ou vertex) qui définissent les extrémités
de ces segments. Ces éléments (points, lignes, triangles) sont
aussi appelés primitives. OpenGL est basé sur le principe des
primitives, c'est-à-dire que pour dessiner un objet, il faut dessiner
toutes ses primitives (ca parait logique). Et pour cela, on utilise des fonctions
très simples d'utilistation et permettant des dessins très poussés,
puisque grâce à ces fonctions, on peut dessiner quasiment tout.
Passons maintenant à la pratique : comment dessiner un élément
primitif ? Hé bien vous l'aurez sûrement deviné en lisant
le code d'exemple du triangle : on appelle glBegin()
avec comme paramètre l'élément, on lui envoie les coordonnées
des vecteurs-clés via glVertex(),
et on tremine avec glEnd(). Ultra
simple, non ?
Notez que vous ne verrez rien si vous n'applez pas SwapBuffers(DC).
Pourquoi ? Parce qu'on utilise une technique appelée double-buffering,
qui consiste à afficher une image pendant que l'on calcule l'autre, et
lorsque celle-ci est terminée, on échange les deux. Donc si on
enlève SwapBuffers(DC), on
verra toujours un écran vide, tandis qu'on dessinera dans un écran
non visible. Si vous travaillez en mode simple-buffering (changez l'option dans
SetupPixelFormat() pour les windows-lover,
et dans glutInit() pour les glut-lover),
il faut remplacer SwapBuffers() par
glFlush(). Mais c'est stupide de n'utiliser
qu'un seul buffer, car la construction de l'image est alors visible, ce qui
provoque un effet de scintillement.
Voyons maintenant ce que l'on peut dessiner à part des triangles :
| Paramètre transmis à glBegin |
Description |
Exemple |
GL_POINTS |
Dessine un point pour chaque vertex transmis. |
 |
GL_LINES |
Dessine des lignes. Le point n défini le début d'une ligne
et le point n+1 la fin de la ligne. |
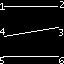 |
GL_LINE_STRIP |
Dessine un groupe de lignes connectées, formant une chaine partant
du premier vertex et s'arrêtant au deriner. |
 |
GL_LINE_LOOP |
Même chose que GL_LINE_STRIP, mais en revenant au premier vertex
à la fin. |
 |
GL_TRIANGLES |
Chaque triplet de vertex constitue un triangle |
 |
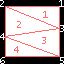
GL_TRIANGLE_STRIP |
Un triangle est défini pour chaque vertex présenté
après les deux premiers |
 |
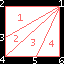
GL_TRIANGLE_FAN |
Même chose que GL_TRIANGLE_STRIP, sauf que le premier vertex de
chaque triangle est toujours le n°1 |
 |
GL_QUADS |
Chaque quadruplet de vertex définit un quadrilatère (composé
de 2 triangles) |
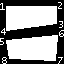 |
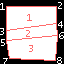
GL_QUAD_STRIP |
Chaque couple de vertex présenté après la première
paire définit un quadrilatère (attention à l'ordre
des points) |
 |
GL_POLYGON |
Dessine un polygone convexe |
 |
Remarque : les lignes rouges et les numéros sur les exemples servent
seulement à montrer comment sont dessinés les primitives, mais
ne sont pas visibles en réalité.
Tout-à-l'heure, j'ai parlé de glVertex(),
et pourtant dans mon exemple il y a écrit glVertex2d().
Pourquoi ? Hé bien parce qu'en fait il y a une multitude de fonctions
pour dessiner des sommets. En fait, on appelle toujours la fonction glVertexxy[v](),
où :
- x définit le nombre de dimension, de 2 à 4. Lorsqu'il y a
2 dimensions, on définit x et y, et z est par défaut à
0. Pourquoi aller jusqu'à 4 dimensions alors qu'on fait de la 3D ? C'est à cause des coordonnées homogènes.
C'est un concept mathématique qui permet d'effectuer toutes les transformations 3D nécessaires simplement avec
des matrices 4x4 et des vecteurs 4D. En pratique, vous n'avez pas à toucher à cette 4e dimension, elle prend
normalement toujours la valeur de 1. Si vous voulez en savoir plus, allez faire un tour dans le redbook ou sur
des sites de maths.
- y définit le type des paramètres : 'i' pour int, 's' pour
short, 'f' pour float, et 'd' pour double.
- Lorsque l'on rajoute 'v', on passe comme paramètre un pointeur sur
les coordonnées plutôt que les coordonnées elles-même
Vous vous servirez en fait principalement de GL_TRIANGLES et GL_QUADS.
Mais là nous allons nous servir de GL_LINES. En effet, maintenant
que vous savez dessiner les primitives (donc que vous savez tout dessiner),
nous allons étudier les transformations de base en OpenGL. Et pour cela,
le plus simple est de dessiner un repère tridimensionnel. Votre fonction
Draw() doit donc être :
void Draw() |
{ |
|
|
|
glClear(GL_COLOR_BUFFER_BIT |
GL_DEPTH_BUFFER_BIT); |
glMatrixMode(GL_MODELVIEW); |
glBegin(GL_LINES);
|
glVertex2i(0,0);glVertex2i(0,1);
|
glVertex2i(0,0);glVertex2i(1,0);
|
glVertex2i(0,0);glVertex3i(0,0,1);
|
glEnd();
|
SwapBuffers(DC);
|
// glutSwapBuffers();
pour glut |
glutPostRedisplay(); |
// Uniquement pour GLUT |
} |
|
Mais si vous lancez le programme tel quel, vous ne verrez rien. Pourquoi ?
Parce qu'au départ, nous sommes placé en (0,0,0) et nous regardons
vers le point (0,0,-1). Or notre objet est situé en (0,0,0), donc nous
ne verrons pas grand chose. Pour changer cela, il suffit d'insérer avant
glBegin() :
gluLookAt(3,2,3,0,0,0,0,1,0);
gluLookAt() est une fonction très
simple et puissante permettant de définir un point de vue. Les 3 premiers
paramètres définissent les coordonnées du point de vue,
les 3 suivant l'endroit où il regarde, et les 3 derniers un vecteur qui
dit où est le haut de la caméra. gluLookAt()
effectue les opérations nécessaires sur la matrice active afin
que le repère soit bien orienté. Nous devons donc activer nous-même
la matrice ModelView grâce à glMatrixMode().
Vous pouvez maintenant lancer votre programme, et vous verrez une fenêtre
de ce genre (sans les textes, bien sûr) :
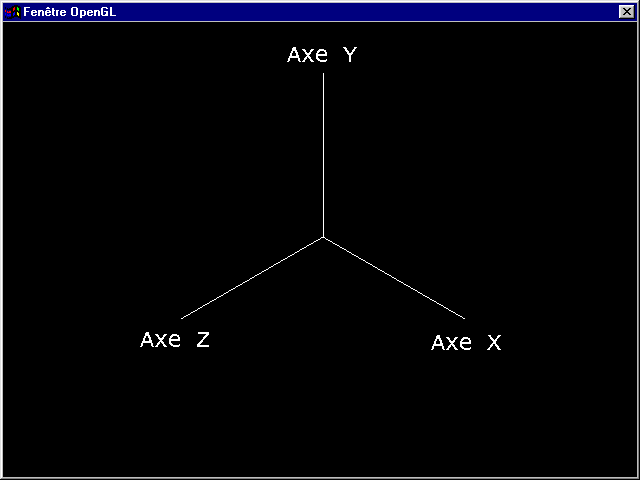
Nous allons maintenant utiliser ce repère pour étudier les transformations,
au nombre de 3. Déclarez d'abord une variable globale double
a=0; et commencons.
Les prinicpes fondamentaux :
- Lorsque vous avez effectué une transformation, tous les objets dessinés
après cette transformation sont affectés, tant que
glLoadIdentity()
n'est pas appelé (auquel cas les objets ne seront plus transformés)
;
- Les modifications affectent directement le repère de coordonnées
et se basent sur le repère de coordonnées. Le axes utilisés
sont donc toujours les axes locaux. C'est-à-dire que si vous
avez fait une rotation autour de l'axe X, et que vous voulez faire une rotation
autour de l'axe Y, cette rotation s'effectuera autour de l'axe modifié
par la première rotation (vous verrez un exemple concret tout-à-l'heure)
;
- Un objet dessiné ne peut plus être modifié.
L'homotétie ( glScalef / glScaled ) :
Il s'agit d'un agrandissement ou une réduction par rapport au centre
du repère de coordonnées. Si vous êtes un habitué
de 3DS, cette fonction revient à faire un Non-Uniform Scaling sur tous
les objets dessinés après. Exemple : insérez avant le glBegin()
de Draw() les lignes suivantes (sans oublier d'inclure math.h
pour les fonctions trigo) :
glScaled(1.-cos(a)/3.,1.+cos(a)/3.,1.+cos(a)/3.);
a+=.1;
Et vous verrez une belle animation dans ce genre :
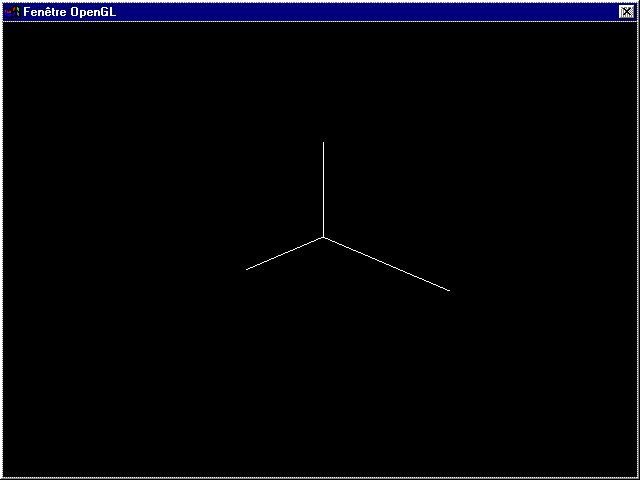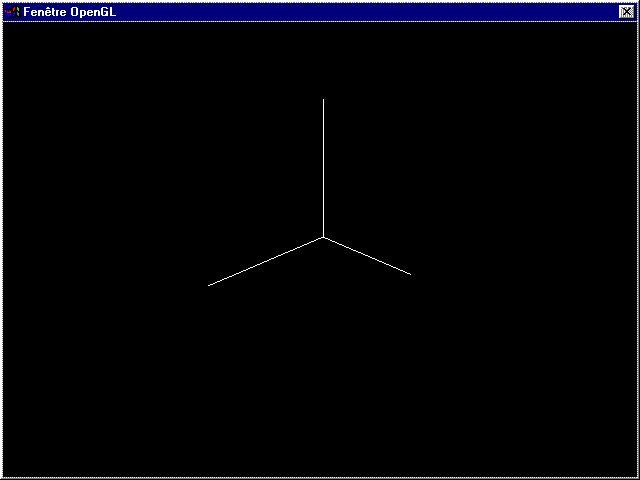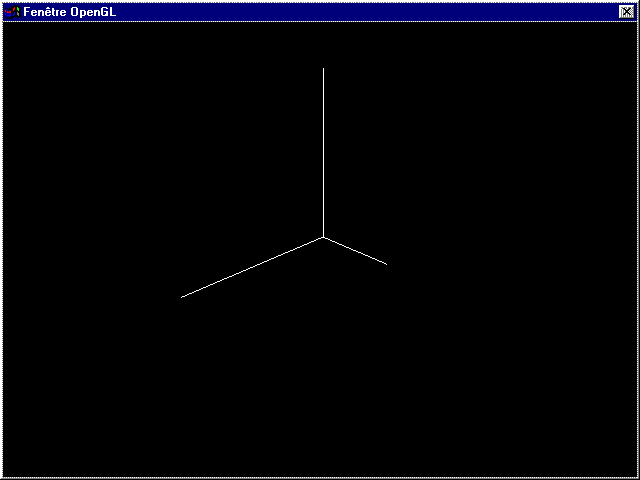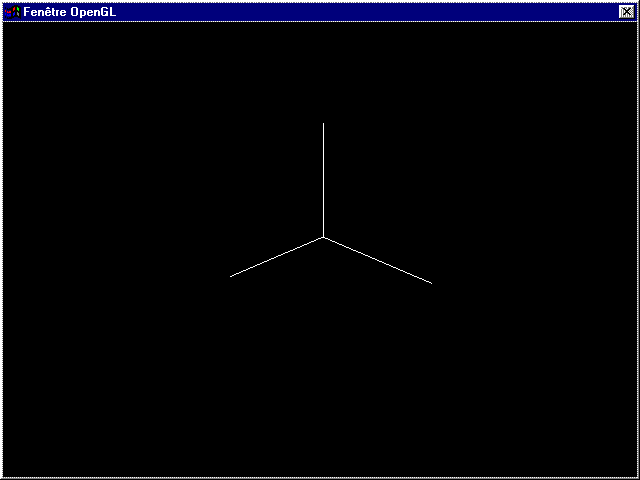
Le repère est agrandi ou réduit selon certains axes. Comme je
l'ai dit précédemment, toutes les transformations qui suivent
seront basées sur le nouveau repère, tant que celui-ci n'aura
pas été réinitialisé par glLoadIdentity(). Donc
vous translatez un objet après avoir effectué une réduction
par glScale(), le déplacement sera plus court, puisque le repère
aura diminué.
la translation ( glTranslated / glTranslatef ) :
C'est en fait un déplacement selon le vecteur passé en paramètre.
Le meilleur moyen de l'expliquer est de fournir un exemple. à la place
du glScaled, écrivez :
glTranslated(cos(a),0,sin(a));
Et ca donne :
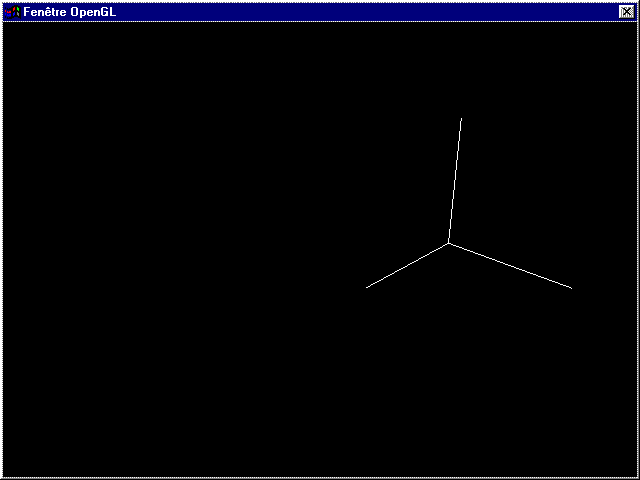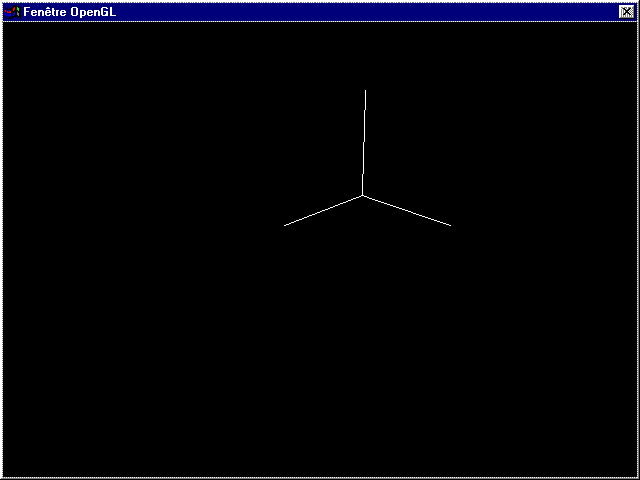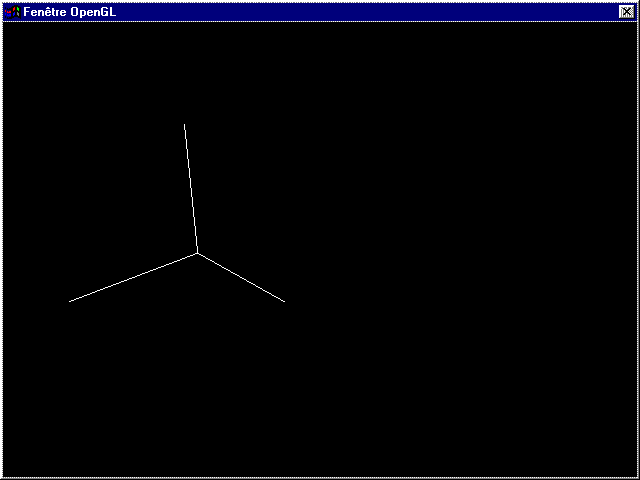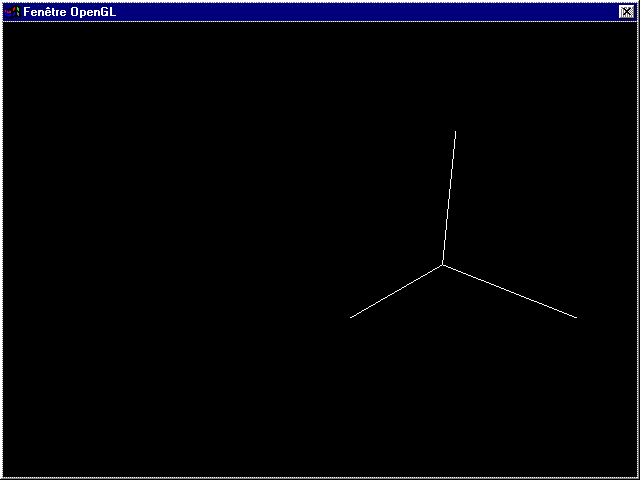
Je ne le répèterais jamais assez : les transformations affectent
aussi le système de coordonnées. Donc si vous avez effectué
une translation, et qu'ensuite vous vouliez faire une homotétie, le centre
de cette homotétie aura lui aussi été déplacé.
la rotation ( glRotated / glRotatef ) :
Elle permet d'effectuer une rotation autour de n'importe quel axe. On lui passe
comme paramètre l'angle en degré et les coordonnées x,y
et z du vecteur de rotation. La rotation fait tout tourner, y compri le repère
lui-même (comme les autres transformations d'ailleurs). Donc si vous faites
une première rotation selon un vecteur v1, et que vous voulez faire une
deuxième rotation selon un autre vecteur v2, n'oubliez pas que v2 a lui
aussi subi la première rotation ! Un petit exemple ?
glRotated(a*180/3.14,1,1,1);
donne :
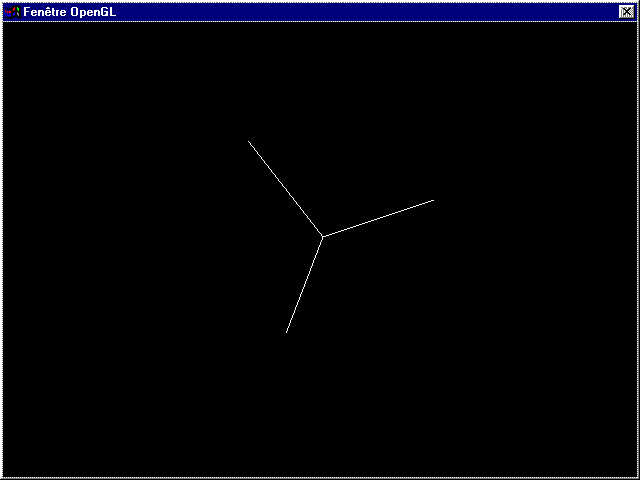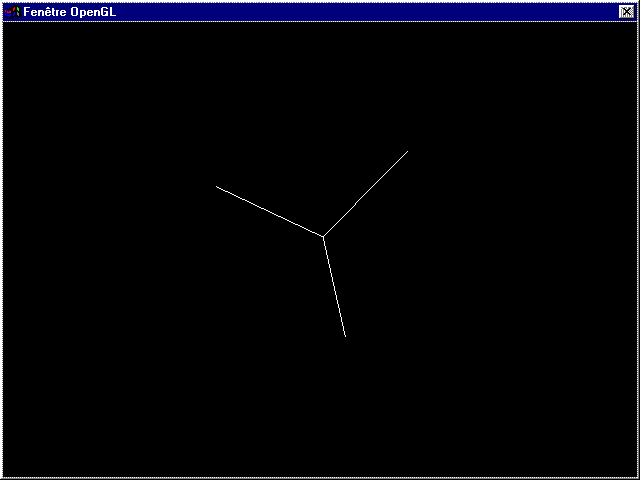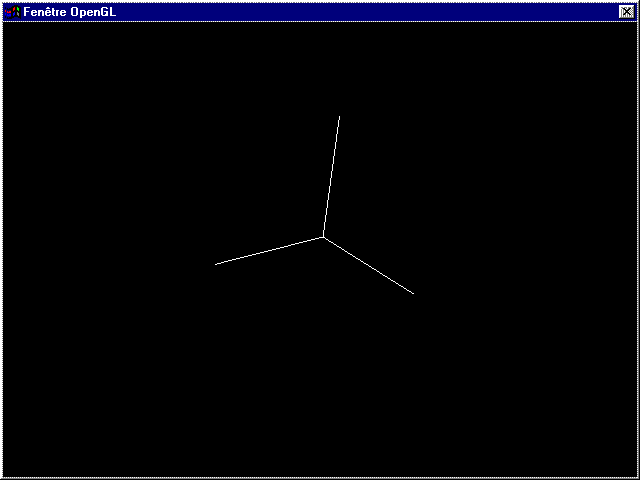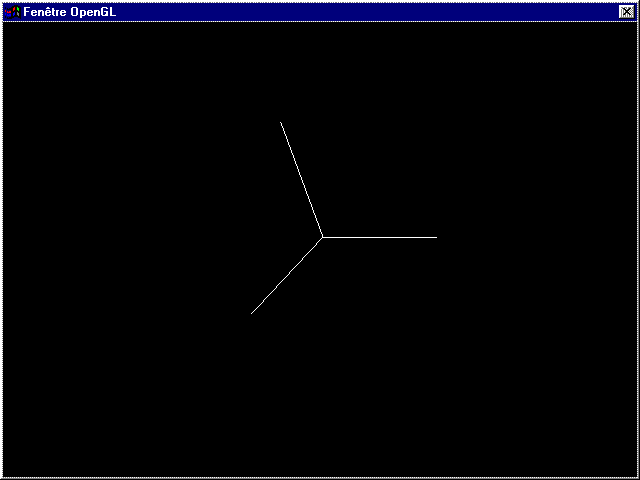
Vous pouvez bien sûr combiner les transformations. Essayez par exemple
les 3 en même temps, c'est assez sympa.
Et voilà ! Vous savez tout sur le dessin et les transformation et OpenGL.
Vous pouvez donc maintenant tout dessiner ! Bon, OK, c'est lourd de dessiner
une mobylette à la mano, mais en fait glu vous permet d'y arriver plus
facilement : elle fournit des primitives moins primitives, avec gluSphere, gluDisk,
gluCylinder, gluPartialDisk... Etudiez ces fonctions avec F1, et amusez-vous
à dessiner de petits objets et à tourner autour. Je vous rapelle
que le meilleur moyen d'apprendre est encore d'apprendre par soi-même.
Donc entraînez-vous à manier les transformations et les primitives
jusqu'à ce que vous vous soyez bien familiarisés avec.
La prochaine fois, nous verrons le coloriage, alors préparez vos crayons
de couleurs ;-)
Antoche | |