OpenGL : les spots

1. Les normales

Je dois vous avouer un truc : je vous ai caché quelque chose. Pas une petite chose sans importance, mais vraiment un gros truc, qui mérite pas mal de pages dans un bon bouquin. Et ce truc, c'est les normales. Si vous êtes accros des bons bouquins sur les modeleurs 3D, vous devez en avoir entendu parler, car il n'y a pas de lumière sans normales. Laissez-moi vous expliquer : vous savez déjà que lorsque un objet illuminé, il est coloré par 3 couleurs : ambiente, diffuse et spéculaire. Pour trouver la lumière ambiente, c'est pas dur : on multiplie les composantes ambientes du matériau par celle de la lumière et paf on applique ça à toutes les faces :
Ambiente(R/G/B) = AmbienteMatériau(R/G/B) * AmbienteLumière(R/G/B)
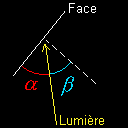Par contre, pour la lumière diffuse, l'intensité de cette lumière dépend de chaque face : si la face est perpendiculaire à la direction de la lumière, l'intensité de la lumière est maximum. Si par contre la face est en biais, la lumière diffuse est plus faible. Et si la face tourne le dos à la source, alors la lumière diffuse est nulle. Donc en gros, pour calculer la lumière diffuse, on multiplie la composante diffuse de la lumière par la composante diffuse du matériau, et ensuite on multiplie ça par le sinus de l'angle entre la direction de la lumière et la face :
Diffuse(R/G/B) = DiffuseMatériau(R/G/B) * DiffuseLumière(R/G/B) * Sin(alpha)
Si on regarde le dessin, et si on sait ce qu'est un sinus et un cosinus (je vais quand même pas redonner les définitions), on remarquera aisément que Sin(alpha) = Cos(Beta). Je suppose que ce n'est un secret pour personne. Donc maintenant, puisqu'on cherche à faire du temps réel, faudrait voir à trouver une forumle suffisamment rapide et autre qu'une table de sin pour trouver ce cosinus (ou ce sinus). Et là, si vous êtes intelligent (ou si avez déjà lu un bouquin quelconque sur la 3D), vous allez me répondre : le produit scalaire ! En effet, pourvu que deux vecteurs soient unitaires, on récupère directement le cosinus entre les deux ! Puisqu'on connait déjà le vecteur lumière, il suffit de trouver l'autre, en pointillés sur le shéma, orthogonal à la face. Et ce vecteur orthogonal, ou vecteur normal (et oui, c'est ça !), comptez pas sur OpenGL pour le trouver tout seul. Et oui, c'est vous qui devez lui dire quelle est la normale de chaque face. Et si je ne vous en ai jamais parlé auparavant, c'est tout simplement parce que GLUT calculait lui-même les normales dans glutSphere(), donc on n'avait pas à s'en préoccuper. Donc la formule de la lumière diffuse est :
Diffuse(R/G/B) = DiffuseMatériau(R/G/B) * DiffuseLumière(R/G/B) * (VecteurLumière.Normale)
De même, la lumière spéculaire s'obtient en vérifiant si les rayons de lumière, réfléchis par la face, sont dirigés vers la caméra. Et pour savoir dans quelle direction est réfléchie la lumière, il faut aussi connaître la normale de la face.

2. Per vertex lighting

En fait, OpenGL ne calcule pas les lumières face par face, mais sommet par sommet. En effet, si la lumière était calculée pour chaque face, alors toutes les faces auraient une couleur uniforme, ce qui ferait apparaître les arêtes entre les faces (ce qu'on appelle le flat shading), et en plus il faudrait calculer le centre de gravité de la face pour connaitre la direction du vecteur lumière. Alors que si la lumière est calculé sommet par sommet, non seulement on connait tout de suite la direction du vecteur lumière, mais en plus si deux sommets sont illuminés différemment, on fait un petit dégradé entre les deux au moment du remplissage de la face, et hop on voit plus les arêtes. C'est ce qu'on appelle le gouraud shading. Mais on voit aussi l'inconvénient : moins il y a de sommets, et moins la tache de lumière sera précise. Laissez-moi vous expliquer ceci en images :
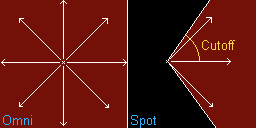
Les deux images sont les mêmes : il s'agit d'un plan illuminé par un spot rouge. Sauf que sur l'image de gauche, le plan est constitué par une grille de quelques points alors qu'à droite les mailles de la grille sont beaucoup plus reserrées. Vous voyez bien que plus il y a de points, et plus l'image est réaliste. Mais aussi s'il y a plus de points, l'image demandera plus de temps de calcul.
En fait, l'idéal serait de faire du per pixel lighting, c'est-à-dire que la lumière serait calculée pour chaque pixel de la face, au moment du remplissage de la face (ca donne ce qu'on appelle le phong shading). Evidemment, là ca serait parfait, quel que soit le nombre de sommets, mais ce serait tellement lent qu'on ne pourrait plus appeler ca du temps réel. C'est donc une technique qui n'est utilisée que dans les modeleurs, où la qualité prévaut sur la vitesse.
En fait je vous dis ça pour une bonne raison : c'est que dans ce tutorial, pour voir les spots, on va s'amuser à éclairer un mur avec des spots et voir ce que ca donne. "Pas compliqué de dessiner un mur : on fait un petit glBegin(GL_QUADS), 4 glVertex(), un glEnd() et c'est fini", me diriez-vous. Et ben non justement. Parce que si on fait ca, on aura juste 4 sommets aux 4 coins, ca risque de faire un peu trop juste pour voir la tache d'un spot. Donc il faut que notre mur soit en fait une grille plane, de façon à ce qu'on distingue bien la lumière du spot sur le mur.

3. C'est parti

4. Cutoff

5. Direction

6. Exposant

Mais ce spot n'est pas super convaincant : la tache a une couleur uniforme, et en plus on distigue trop le crénelage de la grille. Généralement, un spot éclaire plus fort au centre et moins sur le bords. Pour reproduire cet effet, on ne dispose pas comme dans 3DS d'un 'hotspot' et d'un 'falloff', mais on a quand même un truc y ressemblant : l'exposant du spot. En effet OpenGL est capable de diminuer exponentiellement l'intensité de la lumière du spot en fonction de la distance par rapport au centre de la tache. Pour accentuer ce dégradé on peut modifier le facteur expotentiel : plus il est grand et plus la lumière sera faible sur les bords. Un petit exemple pour mieux expliquer :

5	10	20	30	128 (max)

Comme vous pouvez le voir, non seulement la tache du spot est beaucoup plus réaliste, mais en plus on ne distingue plus le crénelage de la grille à partir d'un certain niveau. Pour changer cet exposant, il suffit bien sûr d'appeler glLight() avec comme argument GL_SPOT_EXPONENT. Les spots peuvent également bénéficier de l'atténutation en fonction de la distance, comme pour toute lumière ponctuelle. Notez qu'on ne peut pas faire de spots avec une lumière directionnelle, puisque, la source étant à une distance infinie, on ne peut tenir compte du cutoff.

7. Le LightModel

Notre petit tour sur les lumière ne serait pas complet sans avoir parlé du LightModel. Qu'est-ce que c'est (je dois bien déjà avoir posé cette question un bon nombre de fois) ? Et bien c'est un ensemble de variables d'état qui définissent comment est gérée l'illumination dans OpenGL, sans se rapporter à une source de lumière spécifique. Ces variables sont au nombre de 3 : la lumière ambiente (GL_LIGHT_MODEL_AMBIENT) de la scène, le modèle de vue (GL_LIGHT_MODEL_LOCAL_VIEWER) et le modèle double face (GL_LIGHT_MODEL_TWO_SIDE). Pour changer une de ces variables, on appelle la fonction glLightModel{if}[v](paramètre, valeur), où paramètre est le nom de la variable à modifier (GL_LIGHT_MODEL_BIDULE), et valeur la valeur à assigner à cette variable.

• La variable GL_LIGHT_MODEL_AMBIENT est, comme son nom a l'air de l'indiquer, la lumière ambiente de la scène entière. En fait, lorsque la gestion des lumière est activée, il y une source qui est toujours présente, et qui émet une lumière ambiente sur tout les objets. La valeur par défaut de cette lumière est (0.2, 0.2, 0.2, 1.0) (ne vous préoccupez pas du 4e paramètre). Pour la modifier, il suffit d'appeler glLightModel{if}v() avec comme nouvelle valeur un tableau de 4 valeurs (int ou float, suivant la fonction).
• La variable GL_LIGHT_MODEL_LOCAL_VIEWER est le pendant des lumières directionnelles/ponctuelles pour la caméra. En effet, lorsque la lumière spéculaire d'une face est calculée, elle résulte d'une opération entre le vecteur lumière->objet et le vecteur caméra->objet. Dans la réalité, tous les vecteurs caméra->objet rayonnent à partir du centre de la caméra, un peu comme une lumière ponctuelle rayonne à partir de sa position. On dit alors que le point de vue est local. Ceci oblige OpenGL à recalculer le vecteur caméra->objet à chaque fois qu'il a besoin de calculer la composante spéculaire d'un sommet. Pour accélérer un peu les choses, on peut lui dire que tous les vecteurs caméra->objet sont parallèes à l'axe z de la caméra, comme pour une source directionnelle, où tous les veteurs lumière sont parallèles. Cela diminue le réalisme, mais la vitesse de rendu est sensiblement augmentée. Plus le FOV de la caméra sera grand, et moins le calcul de la lumière semblera réaliste. Par défaut, le modèle local est désactivé (GL_LIGHT_MODEL_LOCAL_VIEWER = 0). Pour l'activer, il suffit d'affecter à la variable une valeur différente de 0.
• Et enfin, GL_LIGHT_MODEL_TWO_SIDE définit si on travaille en illumination simple ou double face. Attention, si vous êtes en simple-face, cela ne veut pas dire qu'OpenGL ne dessinera que la face avant et pas la face arrière (pour cela il faut utiliser glEnable(GL_CULL_FACE)), mais que le matériau attribué à la face avant sera utilisé pour la face arrière, et que la normale sera la même pour les deux cotés. Si par contre l'illumination est en double-face, la face arrière sera dessinée avec son propre matériau, et sa normale sera l'opposée de celle de la face avant. Pour définir à quel coté (avant ou arrière) de la face on affecte tel ou tel matériau, il faut spécifer GL_FRONT, GL_BACK, ou GL_FRONT_AND_BACK comme premier paramètre de glMaterial() (se reporter aux tutorials précédents). Si GL_LIGHT_MODEL_TWO_SIDE est à 0 (défaut), le modèle simple-face est défini. Sinon, on est en mode double-face.

Et bien voilà, on a fait le tour complet des sources de lumières. Vous pouvez maintenant faire ce que vous voulez avec les lumières pour créer votre petite disco personnelle. Pour ceux qui se poseraient des questions, je rapelle quand même qu'OpenGL est un moteur temps réel basique, et que même s'il est professionnel, il ne gère tout de même pas les ombres ou autres réflections. Si vous en voulez, vous serez obligé de les calculer vous-même. Il existe plusieurs méthodes, plus ou moins rapides et réalistes, peut-être en parlerais-je plus tard. Pour les impatients, allez voir sur le site de sgi, vous aaurez pas mal d'infos là-dessus (en anglais, bien sûr). En attendant le prochain tutorial, sur les textures, je vous propose de lire la petite annexe ci-dessous :

Annexe : Calculer les normales

Dans l'exemple que je viens de vous montrer, on n'a pas vraiment eu de mal à calculer les normales des points du mur. Mais il se pourrait bien que vous ayez quelques fois des normales à calculer autrement plus complexes, notemment si vous importez des modèles 3DS ou ASE, où les normales ne sont pas forcément spécifiées. Voici donc quelques techniques couramment utilisées pour calculer les normales.
Essayons d'abord de calculer une normale unique pour tous les sommets d'un triangle. Si vous avez des notions de maths, vous aurez remarqué qu'un vecteur normal à un plan peut être obtenu à partir de deux vecteurs de ce plan, du moment qu'ils ne sont pas colinéaires. Et bien nous somme gâtés : dans un triangle, il y a trois côtés, donc 3 vecteurs : il suffit d'en prendre 2 et d'en faire le produit vectoriel, et nous avons notre normale (attention à l'ordre du produit vectoriel : il faut que la normale soit orientée dans le bon sens !). Il faut ensuite la normaliser (c'est-à-dire faire en sorte que sa norme soit égale à 1) pour que le produit scalaire donne directement le cos(Beta), en divisant chaque composante par la norme du vecteur, car sinon les calculs seront faussés. Notez qu'OpenGL peut normaliser les normales pour vous (il suffit pour cela de faire glEnable(GL_NORMALIZE) ), mais ce sera au détriment de la rapidité. Donc maintenant que nous avons la normale de notre face, il suffit de l'appliquer aux 3 sommets et c'est fini.
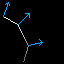Mais ce n'est pas totalement satisfaisant : cela nous donnera du flat shading : il n'y aura pas de dégradé entre les sommets, et on verra distinctement les arêtes, comme dans la piètre image que vous voyez au dessus. Pour qu'on ne voie pas les arêtes, ce qu'il faudrait, c'est que deux sommets ayant les mêmes coordonnées aient la même normale, quelle que soit la face à laquelle ils appartiennent. Donc il faut parcourir les sommets et lorsqu'on en trouve plusieurs au même endroit, on fait la moyenne des normales de ces sommets et on leur attribue à tous cette normale moyenne. Et là ch'est machik : cha marche !

Voilà le tutorial est terminé. Si vous avez des questions, vous savez à qui vous adresser. Dans les sources à télécharger se trouve un petit programme qui montre 3 spots se courant après.