Projets image 2006 :
Contours actifs (snakes) 3D
Lorsqu'on cherche à détecter des contours sur une image, on travaille
localement sur une petite partie de l'image. Dans l'agorithme utilisé, il est
justement question de déterminer une région locale sur le polyhèdre (3D) à
partir du snake (contour actif) tracé par l'utilisateur.
Nous avons décidé de ne travailler que sur des meshs triangulés, le cas plus
général n'étant pas de grand intérêt quand à l'interprétation des résultats
obtenus pour les algorithmes utilisés.
Une fois que l'on a déterminé cette région locale (nous l'avons fait en
utilisant comme intermédiaire un fichier .OFF), on la paramétrise sur un
polygone (2D) convexe pour optimiser les calculs matriciels d'évolution du
snake (processus de minimisation de l'énergie caractéristique). Ces calculs
consistent surtout en des résolutions matricielles LU.
CGAL 3.2 offre des fonctionnalités pour la paramétrisation de mesh, mais
cette bibliothèque n'a pas été installée, ce que nous regrettons. Nous avons
donc choisi d'utiliser un carré pour la paramétrisation, qui est un cas
facile à mettre en oeuvre.
Par rapport aux fichiers .OFF utilisés, après calcul de la distance maximale
entre 2 sommets d'un polyhèdre, il est apparu qu'un carré de côté 6 unités
serait intéressant pour des régions locales de moins de 800 sommets (cas le
plus fréquent).
Forme de la région paramétrisée
Le premier problème rencontré, c'est le choix des 4 points de la région
locale que l'on va associer aux 4 coins du carré. En effet, on imagine bien
qu'un mauvais choix à ce stade, entraînera une mauvaise paramétrisation,
c'est-à-dire une paramétrisation dans laquelle il y a beaucoup de distorsion
par rapport à la région locale 3D. Il faut prendre cela en considération, car
sinon notre minimisation énergétique ne reflètera pas la réalité, à cause du
calcul de dérivées partielles dans le processus de minimisation qui prend en
compte les positions 2D des points de la région locale.
Il est clair, vu la complexité des meshs rencontrées, qu'il serait plus
efficace de demander à l'utilisateur de fixer lui-même ces 4 points sur la
mesh 3D.
Une autre façon de faire, serait de choisir les 4 points extrémaux du mesh
3D. Si on choisit les 4 sommets en se basant sur le nombre d'arètes sur le
bord, c'est-à-dire si l'on prend un sommet puis un autre situé à 1/4 des
arètes plus tard, etc..., on aura un mauvais résultat à cause de la forte
variation de la longueur des arètes de la région locale. Une méthode plus
appropriée consiterait à calculer le périmètre de la région locale, puis de
fixer les 4 points du carré sur 4 points du bord de la région locale situé à
0, 1/4, 1/2 et 3/4 du périmètre. C'est ce que nous avons choisi de tester
dans un premier temps.
Une fois les 4 coins du carré associés à 4 sommets du bord de la région
locale, on peut facilement associer tous les points de la bordure de la
région à des points 2D sur la bordure du carré en utilisant des ratios de
longueur d'arète (distance parcourue sur un côté de la région / longueur
totale de ce côté). Nous avons eu quelques problèmes à cause de CGAL, car son
itérateur sur les arètes du bord de la région locale renvoyait des arètes non
successives. Donc nous avons du créer notre propre circulateur de bord de
polyhèdre.
Coefficients de la paramétrisation
Ensuite, pour déterminer tous les points intérieurs 2D du carré
correspondant aux points intérieurs de la région locale, on utilise la
méthode de Floater (cf sujet), qui consiste à utiliser des combinaisons
convexes des sommets voisins. Nous avons choisi simplement l'isobarycentre,
en prenant les lamba_i_j=1/nombre_de_voisins_du_sommet_i (paramétrisation
uniforme). Une fois les lamba_i_j calculés, il suffit de résoudre un système
matriciel. Nous avons choisi de le faire en utilisant la méthode LU, qui est
recommandée dans tous les articles lus.
Ce qui ressort d'une manière générale sur les résultats obtenus, c'est une
grande distorsion. Cette distorsion est due :
- à la petite "épaisseur" de la région locale (en effet tous les sommets de la région locale ont été choisis tels qu'ils soient adjacents à au moins un sommet du snake) ;
- et aux difformités des régions locales.
Il y a aussi une influence du choix des 4 points de la bordure qui sont
associés aux 4 coins du carré, mais cela n'a pas trop d'importance lorsqu'une
région locale a une forme indescriptible (Pour certaines régions, il serait
même difficile de demander à un utilisateur de fixer les 4 points à la main).
Par exemple, on peut avoir des régions "serpentées" ou en zig-zag.
On peut être assez satisfait de notre méthode utilisée pour la répartition
des points du bord sur le carré, et aussi de la taille de 6 unités pour le
côté du carré. Par contre, la région locale obtenue n'est pas acceptable: sa
petite taille entraîne une forte distorsion. Cela peut être résolu en
utilisant une frontière virtuelle (virtual boundary), ou carrément en
rajoutant une couche supplémentaire de facettes à notre région locale (ce qui
revient au même du point de vue temps de calculs).
Problèmes rencontrés, solutions imaginées
Rappelons les problèmes vus ci-dessus :
- Si on choisit le carré, comment fixer 4 points de la bordure 3D aux 4 sommets du carré ?
- Sur quel polygone convexe 2D doit-on paramétriser la région locale 3D ?
- Quelle combinaison convexe doit-on choisir ?
Sinon, nous avons été confrontés aux problèmes suivants :
le problème des trous dans une région locale se produit lorsque 2 parties du snake se rapprochent suffisamment ou lorsqu'il y a deux points du snake qui sont confondus (par exemple un cercle). Pour résoudre ce problème, nous avons trouvé deux solutions.
- une amélioration de la région locale, en remplissant les trous et en éliminant les concavités en rajoutant les facettes nécessaires.
- ou bien : segmenter le snake, de telle sorte que chaque morceau du snake possède une région locale sans trou, et ensuite de continuer le processus de minimisation énergétique sur chaque morceau de manière indépendante. Cette dernière est sans doute la plus intéressante, parce qu'elle évite de faire des calculs supplémentaires pour "homogénéiser" la région locale, tout en limitant la taille des systèmes matriciels que l'on doit résoudre.
Dans cette partie, ce qui a semblé le plus important, c'est d'avoir un moyen rapide de passer de la région locale 3D à sa paramétrisation 2D. En effet si on veut voir l'évolution 3D du snake au fur et à mesure, on doit faire des interpolations des voisins 3D associés aux voisins 2D de la facette où se trouve un point du snake. Nous avons commencé par utiliser 2 meshs, la région locale et sa paramétrisation correspondante, en se basant uniquement sur un ordre identique des sommets, arètes et facettes pour passer du 2D au 3D. Mais par la suite, il est apparu moins coûteux d'utiliser un
Mesh
contenant des points 3D avec un champ de type Point 3D en plus
pour représenter le point 2D de la mesh paramétrisée. Même s'il y a une
surcharge de la structure initiale, cela permet de n'avoir qu'un seul
paramètre Mesh dans notre région locale associée au snake, mais
aussi d'accéder aux voisins en temps quasi constant (cela dépend seulement du
nombre de voisins). C'est ce qu'on fera dans la prochaine version.A première vue, il peut paraître bizarre d'utiliser des points 3D pour représenter un mesh 2D, mais cela nous a en fait permis d'utiliser la structure de mesh issue de CGAL fournie au départ et donc d'avoir accès à pas mal de méthodes.
Voici quelques résultats:
| Région locale 3D | Région locale paramétrisée | Nb Sommets | Nb Faces | temps de calcul - Paramétrisation |
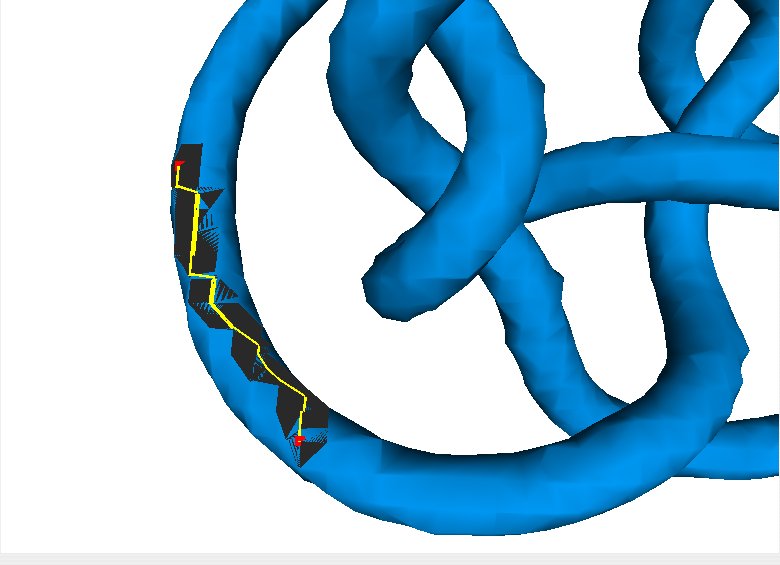 |
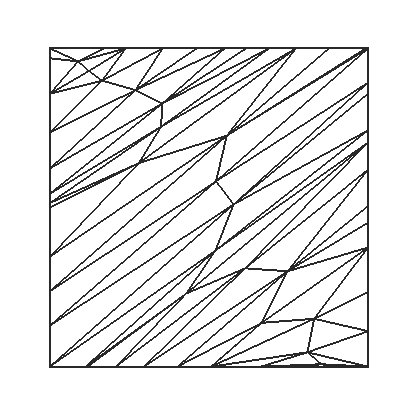 |
63 | 79 | 0,05s |
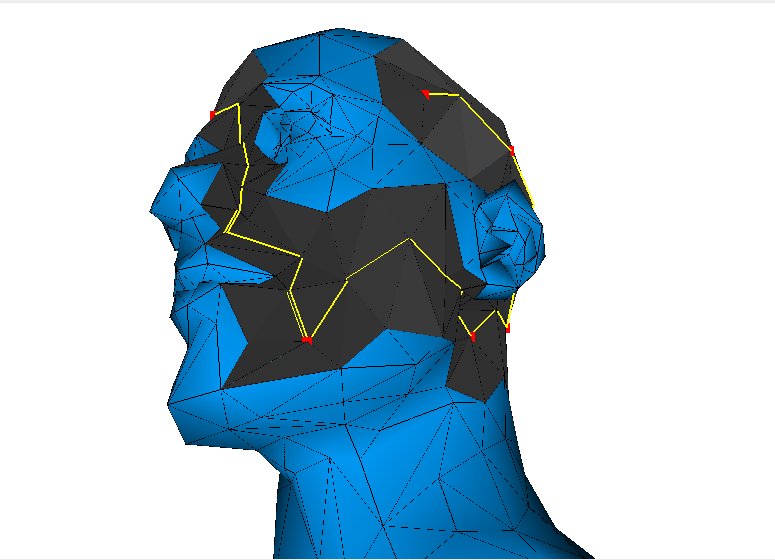 |
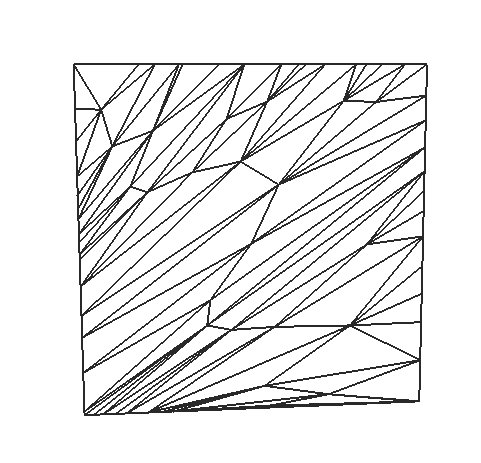 |
82 | 104 | 0,06s |
 |
no image available for the time being |
461 | 583 | Bus error |