


Outils Mathématiques: Position, Orientation et Mouvement
DEA IVR
François Faure
, UJF-Grenoble
Ce cours est une introduction aux techniques permettant de définir les mouvement de points et solides dans l'espace. Il se compose de quatre séances d'1h30:
- rappels mathématiques (algèbre linéaire, géométrie euclidienne, matrices)
- positionnement (repères, rotations, chaînes cinématiques)
- cinématique (vitesses et accélérations, lois de composition)
- cinématique inverse (contrôle de mouvement)
| Définition |
Exemple |
| Ensemble |
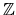 |
| muni d'une loi de composition interne |
+ |
| associative |
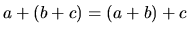 |
| munie d'un elément neutre |
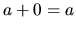 |
| tout élement a un symétrique |
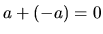 |
Si l'opération est commutative (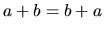 ) alors le groupe est dit commutatif.
) alors le groupe est dit commutatif.
1.1.3 Sous-espaces vectoriels
combinaison linéaire: Une combinaison linéaire d'une partie  de
de
 est:
est:
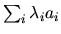 , avec
, avec 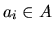
sous-espace vectoriel (SEV): Un sous-espace vectoriel de
 est une sous-ensemble de
est une sous-ensemble de
 stable par combinaison lineaire.
stable par combinaison lineaire.
Exemple: une droite vectorielle est un SEV de
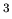 .
.
SEV engendré par une partie A de
 : L'ensemble des combinaisons linéaires des vecteurs de A.
: L'ensemble des combinaisons linéaires des vecteurs de A.
Exemple: plan vectoriel engendré par deux vecteurs non colineaires.
somme de SEV
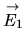 et
et
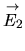 de
de
 :
:
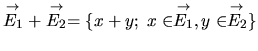 .
La somme de deux SEV est un SEV. L'intersection aussi. Si l'intersection de deux SEV est nulle, la somme est dite directe et notée
.
La somme de deux SEV est un SEV. L'intersection aussi. Si l'intersection de deux SEV est nulle, la somme est dite directe et notée
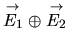
Exemple dans
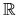
 : la somme de deux droites vectorielles distinctes est directe et c'est un plan vectoriel.
: la somme de deux droites vectorielles distinctes est directe et c'est un plan vectoriel.
1.1.4 Systèmes de vecteurs, bases
système de vecteurs: ensemble
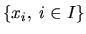 où
où 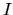 est un ensemble fini de cardinal p, appelé ordre du système
est un ensemble fini de cardinal p, appelé ordre du système
système linéairement indépendant: système de vecteurs dans lequel
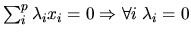
système lié: système non linéairement indépendant
base d'un EV: système libre
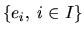 de vecteurs de
de vecteurs de
 tel que pour tout élément x de
tel que pour tout élément x de
 il existe une decomposition unique
il existe une decomposition unique

base orthonormée: Base dont tous les vecteurs sont orthogonaux deux à deux (orthogonalité définie en section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
base orthonormée directe: En dimension 3, base orthonormée dont les vecteurs sont orientés comme le pouce, l'inde et le majeur de la main droite. Par extension, base construite (ou constructible) par produits vectoriels successifs. (produit vectoriel défini en section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
rang d'un système: Le rang d'un système vaut 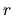 si:
si:
- il existe un système libre extrait de
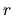 vecteurs
vecteurs
- tout système extrait de
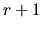 vecteurs est lié
vecteurs est lié
EV de dimension finie: EV qui admet une base de rang fini. Toutes les bases d'un même EV sont de même rang, ce rang est appelé dimension de l'espace.
composantes: Si  est la dimension (finie) d'un EV et
est la dimension (finie) d'un EV et
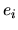
![$ ,\;i\in[1..n]\}$](img35.png) une base, on peut définir un vecteur
une base, on peut définir un vecteur

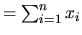
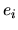 par ses composantes dans la base:
par ses composantes dans la base:
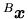
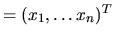
codimension: Si
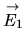 et
et
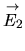 sont deux SEV de
sont deux SEV de
 tels que
tels que
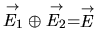 alors la dimension de
alors la dimension de
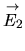 est appelée codimension de
est appelée codimension de
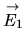 , et réciproquement.
, et réciproquement.
Exemple: dans
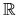
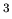 , la codimension d'une droite est 2, la codimension d'un plan est 1.
, la codimension d'une droite est 2, la codimension d'un plan est 1.
hyperplan: SEV de codimension 1
Soit
 un espace vectoriel. Un ensemble E est un espace affine (EA) associé à
un espace vectoriel. Un ensemble E est un espace affine (EA) associé à
 s'il existe une application
s'il existe une application 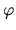 telle que
On note
telle que
On note
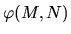
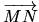 .
.
sous-espace affine: F est un sous-espace affine de E si F est un espace affine associé à un SEV
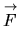 de
de
 . On dit que
. On dit que
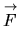 est la direction de F.
est la direction de F.
SEA parallèles: SEA ayant la même direction.
Propriétés:
- l'intersection de deux SEA est un SEA
- par un point donné il passe un unique SEA de direction donnée.
Repère:
Couple 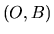 où
où 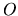 est un point de E et
est un point de E et 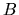 une base de
une base de
 . Pour tout point
. Pour tout point 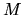 de E,
de E,
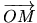
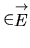 .
.
Un espace est dit euclidien s'il est muni d'un produit scalaire.
Forme bilinéaire, symétrique, définie, positive:
En dimension finie on peut le definir par une matrice A tq:
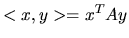 .
.
1.2.2 Normes
norme euclidienne (ou norme indice 2):
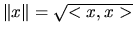
Propriétés:
-
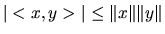
-
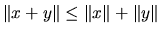 (Minkovski)
(Minkovski)
Autres normes:
- norme indice 1:
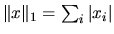 ("distance de Manhattan")
("distance de Manhattan")
- norme infinie:
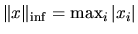
1.2.3 Orthogonalite et othonormalité
orthogonalité:
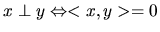
système orthogonal: vecteurs orthogonaux 2 à 2.
vecteur unitaire: vecteur de norme 1.
système orthonormal: système orthogonal de vecteurs unitaires.
base orthonormale: base dont les vecteurs forment un système orthonormal. Dans une base orthonormale, la matrice du produit scalaire est l'identité.
base canonique: dans un espace euclidien, base constituée des vecteurs
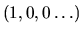 ,
,
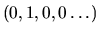 etc.
etc.
SEV orthogonaux:
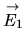 et
et
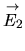 sont des SEV orthogonaux si tout élément de l'un est orthogonal a tout élement de l'autre.
sont des SEV orthogonaux si tout élément de l'un est orthogonal a tout élement de l'autre.
SEA orthogonaux: SEA dont les SEV associés sont orthogonaux.
1.2.4 Produit vectoriel
Soient

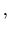
 deux vecteurs en dimension 3. Le produit vectoriel
deux vecteurs en dimension 3. Le produit vectoriel
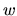


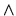
 se calcule par:
se calcule par:
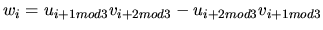
Propriétés:
- si les vecteurs sont liés le produit vectoriel est nul
-

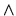

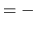

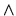

-

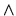

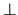

-

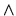

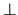

-
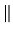

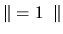

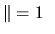

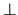

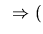



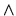

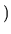 base orthonormée directe
base orthonormée directe
-
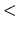

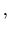

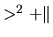

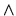

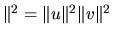
-

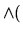

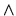
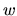
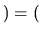

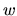
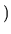

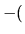


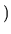
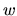
Angles entre vecteurs:
Forme matricielle:
Pour tout vecteur

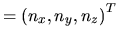 et tout vecteur
et tout vecteur  on a:
on a:
En dimension 3 le produit mixte de trois vecteurs u,v,w est défini par:
Propriétés:
- le produit mixte est nul si les vecteurs sont liés
- le produit mixte est invariant par permutation circulaire:
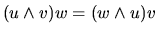
1.3.1 Application linéaire
Application linéaire (AL): Soient
 et
et
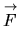 deux espaces vectoriels. Une application
deux espaces vectoriels. Une application
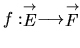 est dite linéaire si elle vérifie:
est dite linéaire si elle vérifie:
endomorphisme: AL de
 dans
dans

composition: la composée 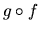 de deux applications linéaires est l'application qui à
de deux applications linéaires est l'application qui à  associe
associe 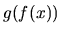 .
La composée de deux AL est une AL.
.
La composée de deux AL est une AL.
image d'un EV par une AL: L'image
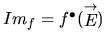 d'un EV
d'un EV
 est un sous-espace vectoriel formé des transformees des élements de
est un sous-espace vectoriel formé des transformees des élements de
 .
.
Exemple: dans
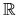
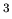 , une projection sur un plan a pour image ce plan.
, une projection sur un plan a pour image ce plan.
image réciproque: L'image réciproque d'un SEV de
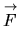 par une AL de
par une AL de
 dans
dans
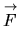 est l'ensemble des élements de
est l'ensemble des élements de
 se transformant en éléments de
se transformant en éléments de
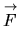 . C'est un SEV de
. C'est un SEV de
 .
.
noyau d'une AL: Le noyau d'une application 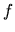 de
de
 dans
dans
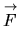 , noté
, noté 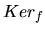 , est l'image réciproque de l'élément nul de
, est l'image réciproque de l'élément nul de
 Exemple: dans
Exemple: dans
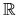
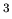 , le noyau d'une projection sur un plan est la droite dans la direction de projection.
, le noyau d'une projection sur un plan est la droite dans la direction de projection.
En dimension finie,
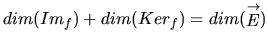
Exemple: Dans un EV de dimension  , projection
, projection 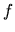 sur une droite.
sur une droite.
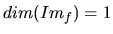 ,
,
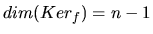
isométrie vectorielle: application linéaire qui conserve le produit scalaire. Transforme une base orthonormale en une base orthonormale.
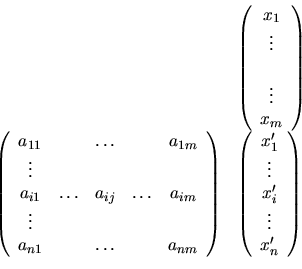
Notons:
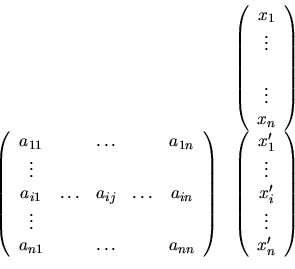
une AL 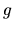 d'un espace
d'un espace
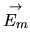 de dimension
de dimension 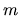 vers un espace
vers un espace
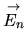 de dimension
de dimension  . Soient les bases:
. Soient les bases:
-
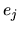
![$ ,\;j\in[1..m]\}$](img123.png) une base de
une base de
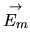 telle que
telle que

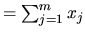
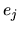 , et
, et
-
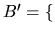
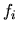
![$ ,\;i\in[1..n]\}$](img35.png) une base de
une base de
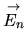 telle que
telle que
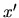
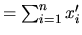
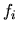
La transformée d'un vecteur de 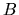 peut s'écrire:
peut s'écrire:
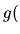
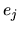
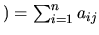
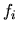 . On peut donc formuler la transformation de
. On peut donc formuler la transformation de  par:
par:
Donc pour chaque composante de 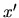 on a
on a
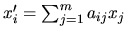 . Nous pouvons ainsi décrire l'application
. Nous pouvons ainsi décrire l'application 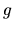 sous forme d'une matrice
sous forme d'une matrice
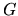 telle que
telle que
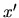

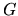

 :
:

Un changement de base est une application lineaire qui aux composantes d'un vecteur dans une certaine base associe les composantes de ce vecteur dans une autre base du même espace.
Soient les bases:
-
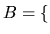
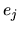
![$ ,\;j\in[1..n]\}$](img144.png) une base de
une base de
 telle que
telle que
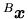
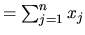
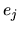 , et
, et
-
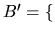
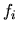
![$ ,\;i\in[1..n]\}$](img35.png) une base de
une base de
 telle que
telle que
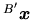
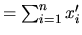
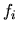
Connaissant
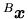 on cherche à déterminer
on cherche à déterminer
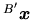 .
Sachant exprimer les vecteurs de B dans B':
.
Sachant exprimer les vecteurs de B dans B':
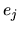
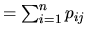
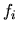 , nous pouvons écrire:
, nous pouvons écrire:
d'où
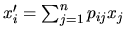 Nous pouvons ainsi décrire le passage de B à B' sous forme d'une matrice
Nous pouvons ainsi décrire le passage de B à B' sous forme d'une matrice
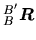 telle que
telle que
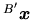

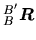
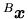
 :
:
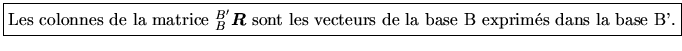
1.3.4 Changement de base d'une application linéaire
Notons:
une AL 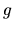 d'un espace
d'un espace
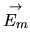 de dimension
de dimension 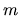 vers un espace
vers un espace
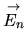 de dimension
de dimension  . Soient
. Soient
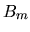 et
et 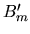 deux bases de
deux bases de
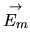
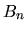 et
et 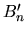 deux bases de
deux bases de
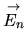
-
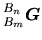 la matrice de
la matrice de  transformant un vecteur exprimé dans
transformant un vecteur exprimé dans 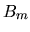 en un vecteur exprimé dans
en un vecteur exprimé dans 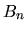 , c'est-à-dire
, c'est-à-dire
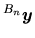

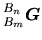
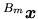
Nous cherchons la matrice équivalente
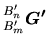 transformant un vecteur
transformant un vecteur
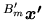 exprimé dans
exprimé dans 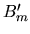 en un vecteur
en un vecteur
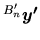 exprimé dans
exprimé dans 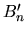 . Le principe est de ramener la donnée dans
. Le principe est de ramener la donnée dans 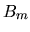 , appliquer
, appliquer 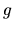 , puis amener le résultat dans la base souhaitée. On peut ainsi écrire:
et donc
, puis amener le résultat dans la base souhaitée. On peut ainsi écrire:
et donc
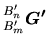

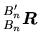
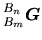
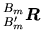
Soit 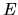 un EA associé à un EV
un EA associé à un EV
 .
Une application
.
Une application 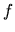 de
de 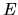 dans
dans 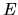 est une application affine (AA) s'il existe un endomorphisme
est une application affine (AA) s'il existe un endomorphisme 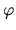 de
de
 tel que pour tout couple
tel que pour tout couple 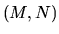 de
de 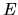 on ait
on ait
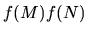
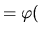
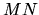
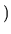
Propriétés:
- une AA est déterminée par la donnée d'un point A, de son transformé A', et de l'endomorphisme associé. L'image M' d'un point M est alors donnée par
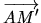

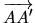
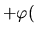
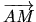
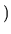
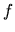 étant donné,
étant donné, 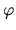 est unique
est unique
- l'image d'un SEA par une AA est un SEA
- la composée de deux AA est une AA. Son endomorphisme associé est la composée des endomorphismes associés.
- l'ensemble des points invariants par une AA est un SEA
- toute AA conserve le barycentre
- deux applications affines sont égales
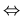 leurs endomorphismes associés sont égaux et il existe un point qui a le même transformé par les deux applications
leurs endomorphismes associés sont égaux et il existe un point qui a le même transformé par les deux applications
Soit un EA 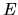 de dimension
de dimension  et les repères:
et les repères:
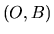 avec
avec 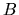 une base de
une base de

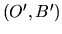 avec
avec 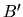 une autre base de
une autre base de

Étant donné
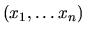 les composantes d'un point
les composantes d'un point 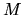 dans le repère
dans le repère 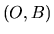 , nous obtenons les composantes
, nous obtenons les composantes
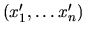 de
de 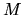 dans
dans 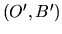 :
:
Soit une application affine définie pour un repère 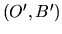 :
Nous désirons calculer la transformée
:
Nous désirons calculer la transformée 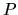 d'un point
d'un point 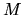 , tous deux définis par leurs coordonnées dans un repère
, tous deux définis par leurs coordonnées dans un repère 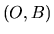 .
Pour cela nous passons
.
Pour cela nous passons 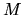 dans
dans 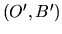 , appliquons la transformation puis ramenons le résultat dans
, appliquons la transformation puis ramenons le résultat dans 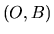 :
:
Une matrice 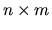 est un tableau de
est un tableau de  lignes et
lignes et 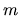 colonnes. Une telle matrice peut servir notamment à représenter:
colonnes. Une telle matrice peut servir notamment à représenter:
- une application linéaire de
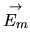 dans
dans
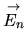
- les coefficients d'un système de
 équations linéaires à
équations linéaires à 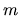 inconnues
inconnues
On notera 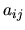 la valeur d'une matrice
la valeur d'une matrice
 en ligne
en ligne 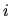 , colonne
, colonne 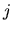 .
.
matrice carrée:

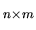 est dite carrée si
est dite carrée si 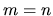 . Dans une matrice carrée, les éléments de (1,1) à (n,n) forment la diagonale principale.
. Dans une matrice carrée, les éléments de (1,1) à (n,n) forment la diagonale principale.
matrice identité: matrice carrée dont les éléments de la diagonale principale valent tous 1, et tous les autres élements, 0. En dimension  , on la note
, on la note 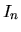 Pour toute matrice
Pour toute matrice

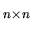 ,
,

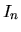

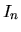



matrice triangulaire: Une matrice est dite triangulaire supérieure (resp. inférieure) si tous les éléments en-dessous (resp. au-dessus) de sa diagonale principale sont nuls.
matrice symétrique: Matrice égale à sa transposée
matrice symétrique définie positive: Une matrice symétrique  telle que pour tout vecteur
telle que pour tout vecteur  non nul,
non nul,
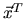


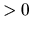
matrice symétrique semi-définie positive: Une matrice symétrique  telle que pour tout vecteur
telle que pour tout vecteur  non nul,
non nul,

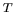


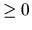
matrice singulière: Une matrice dont les lignes ou les colonnes forment un système lié.
avec
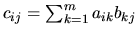 .
.
Si 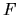 est la matrice associée à une application linéaire
est la matrice associée à une application linéaire 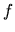 et
et 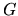 la matrice associée à une application linéaire
la matrice associée à une application linéaire 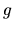 , alors
, alors 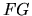 est la matrice associée à l'application linéaire
est la matrice associée à l'application linéaire 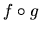 .
.
Les vecteurs en dimension  sont considérés comme des matrices à
sont considérés comme des matrices à  lignes et une colonne.
lignes et une colonne.
La transposée
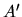
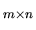 d'une matrice
d'une matrice

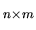 est une matrice notée
est une matrice notée
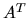 telle que
telle que
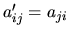 . Transposer une matrice revient à permuter les lignes avec les colonnes.
. Transposer une matrice revient à permuter les lignes avec les colonnes.
Propriétés:
La trace d'une matrice carrée est la somme des élements de sa diagonale.
Propriétés:
L'inverse d'une matrice carrée

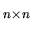 est une matrice carrée
est une matrice carrée

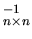 telle que:
telle que:


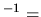

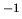


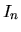 . Une matrice est réversible ssi ses vecteurs colonnes forment un système libre.
. Une matrice est réversible ssi ses vecteurs colonnes forment un système libre.
pseudo-inverse: Une matrice

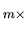 peut admettre une pseudo-inverse
peut admettre une pseudo-inverse

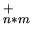 telle que
telle que
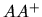

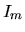 (plus de détails en section
(plus de détails en section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
)
Propriétés:
Matrice carrée dont toutes les lignes ont pour norme 1, sont orthogonales 2 à 2, de même pour les colonnes. Propriétés:
- si
 est orthogonale, alors
est orthogonale, alors

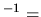

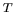 .
.
- Les matrices de changement de base orthonormale sont orthogonales.
Soit  une matrice carrée d'ordre
une matrice carrée d'ordre  .
Le déterminant de
.
Le déterminant de  est un scalaire noté
est un scalaire noté
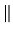

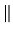 , nul si les vecteurs-colonnes sont liés. Propriétés:
, nul si les vecteurs-colonnes sont liés. Propriétés:
- ne change pas si on ajoute à un vecteur-colonne une combinaison linéaire des vecteurs-colonnes
-
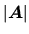

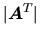
-
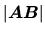

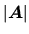
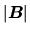
 est inversible ssi son déterminant est non nul
est inversible ssi son déterminant est non nul
Soit 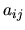 un élément de
un élément de  .
Notons
.
Notons
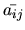 , la matrice de taille
, la matrice de taille
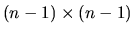 obtenue en retirant la ligne
obtenue en retirant la ligne 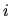 et la colonne
et la colonne 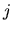 de
de  . Le déterminant de
. Le déterminant de
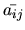 est appelé cofacteur de
est appelé cofacteur de 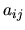 .
.
Calcul par développement de la première ligne:
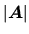
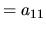
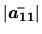
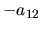
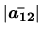
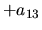
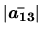
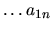
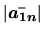
On peut aussi développer par rapport à la première colonne.
Les déterminants d'ordre inférieur peuvent se calculer par la même méthode.
Notons
 la matrice des cofacteurs. L'inverse de
la matrice des cofacteurs. L'inverse de  vaut:
vaut:

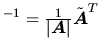 (méthode de calcul extêmement inefficace)
(méthode de calcul extêmement inefficace)
Le déterminant d'une matrice triangulaire est le produit des éléments de sa diagonale principale.
Soit une matrice carrée

 , un vecteur
, un vecteur
 non nul et un scalaire
non nul et un scalaire 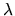 tq:
tq:


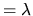
 .
On dit que
.
On dit que 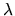 est une valeur propre de
est une valeur propre de  et que
et que  est un vecteur propre de
est un vecteur propre de  associé à
associé à 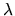 . Notons que pour
. Notons que pour
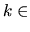
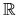 ,
,
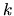
 est aussi vecteur propre.
est aussi vecteur propre.
De la dérivation suivante:
et puisque  est non nul, nous pouvons déduire que les vecteurs-colonnes de
est non nul, nous pouvons déduire que les vecteurs-colonnes de

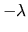
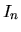 sont liés. Le déterminant de cette matrice est donc nul. Ce déterminant s'exprime comme un polynôme d'ordre
sont liés. Le déterminant de cette matrice est donc nul. Ce déterminant s'exprime comme un polynôme d'ordre  en
en 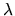 , et les racines de ce polynôme sont les valeurs propres de
, et les racines de ce polynôme sont les valeurs propres de  .
.
La recherche des vecteurs propres associés à une valeur propre 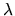 s'effectue en résolvant le système d'équations:
s'effectue en résolvant le système d'équations:
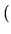

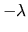
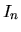

 0. On obtient une famille de solutions qui constitue le sous-espace propre associé à
0. On obtient une famille de solutions qui constitue le sous-espace propre associé à 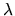 .
.
Propriétés:
- les sous-espaces propres sont des SEV.
- les sous-espaces propres sont orthogonaux entre eux.
- il ne peut y avoir plus de n valeurs propres pour une matrice d'ordre n.
Exemples (dans
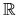
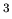 ):
):
- l'identité a une valeur propre:1, et son SEP associé est de dimension 3
- une projection orthogonale sur un plan a deux valeurs propres 1 (SEP associé de dim 2) et 0 (SEP associé de dim 1)
- une rotation a une valeur propre: 1 (SEP associé de dim 1)
Si la somme des SEP a une dimension  égale à celle de la matrice, alors on peut trouver une matrice diagonale équivalente par changement de base. Soit
égale à celle de la matrice, alors on peut trouver une matrice diagonale équivalente par changement de base. Soit 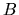 la base dans laquelle sont exprimés les vecteurs-colonnes de la matrice
la base dans laquelle sont exprimés les vecteurs-colonnes de la matrice  , et
, et 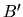 la base constituée par ses vecteurs propres (unitaires). Nous pouvons écrire:
où
la base constituée par ses vecteurs propres (unitaires). Nous pouvons écrire:
où
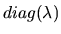 est une matrice diagonale composée des valeurs propres de la matrice associées aux vecteurs-colonnes de la matrice
est une matrice diagonale composée des valeurs propres de la matrice associées aux vecteurs-colonnes de la matrice
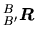 ,
qui sont les vecteurs propres de
,
qui sont les vecteurs propres de
 .
Nous pouvons réciproquement écrire:
.
Nous pouvons réciproquement écrire:
Un système d'équations linéaires peut s'écrire sous forme matricielle



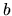 . On est tenté de le résoudre par
. On est tenté de le résoudre par



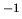
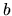 . C'est généralement une mauvaise idée pour deux raisons:
. C'est généralement une mauvaise idée pour deux raisons:
- la matrice peut ne pas être inversible (matrice non carrée ou singulière);
- même quand c'est possible, inverser une matrice est très coûteux.
Voici quelques points de repère très genéraux:
- matrice carrée, non singulière: décomposition LU
- matrice symétrique définie positive: décomposition de Cholesky
- matrice non carrée ou singulière: décomposition en valeurs singulières )SVD)
- matrice creuse: gradient biconjugué
- matrice creuse, symetrique définie positive: gradient conjugué
Les décompositions LU, Colesky et SVD permettent en outre de calculer l'inverse ou le déterminant d'une matrice à un coût raisonnable. À certaines matrices particulières peuvent s'appliquer des methodes spéciales non listées ici. Pour plus de détails, se reporter par exemple à [1].
Dans ce chapitre on considèrera l'espace en dimension 3, sachant que la dimension 2 peut trivialement s'y ramener.
Une rotation est une isométrie dont une direction unique de l'espace (son axe) reste invariante. L'angle maximum entre un vecteur et sa transformée apparaît pour les vecteurs du plan orthogonal à l'axe. C'est par définition l'angle de la rotation.
Nous noterons

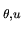 une rotation d'angle
une rotation d'angle 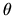 autour de l'axe
autour de l'axe  .
.
- la composée de deux rotations est une rotation.
-
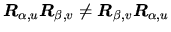 sauf si
sauf si
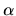
 est colineaire à
est colineaire à
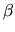

-
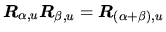
-
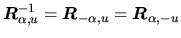
- les matrices de rotation sont orthogonales
- l'espace des rotations est de dimension 3 (9 coefficients de la matrice -3 contraintes de vecteurs-colonnes unitaires -3 contraintes d'orthogonalité)
Les matrices ci-dessous représentent respectivement les rotations

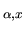 ,
,

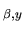 et
et

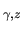 .
.
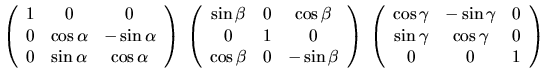 |
(2.1) |
Quand la rotation ne s'effectue pas autour d'un des axes principaux de la base, on peut obtenir son expression matricielle par la décomposition de Jordan:
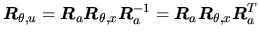 où
où

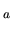 est une rotation qui aligne l'axe
est une rotation qui aligne l'axe  de la base sur l'axe
de la base sur l'axe  de rotation. Un autre vecteur que
de rotation. Un autre vecteur que  peut être choisi. Cette décomposition correspond à un changement de base d'application linéaire comme vu en section
peut être choisi. Cette décomposition correspond à un changement de base d'application linéaire comme vu en section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Cette représentation n'est pas unique car l'alignement est défini à une rotation près autour de l'axe  . On peut en effet remplacer
. On peut en effet remplacer 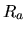 par
par
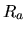
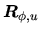 pour tout
pour tout 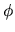 .
.
question: si  est unitaire:
est unitaire:
- que vaut la première colonne de
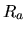 ?
?
- comment en déduire des valeurs pour les colonnes 2 et 3 ?
La formule de Rodrigues fournit un passage direct entre (angle,axe) et matrice de rotation:
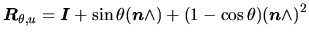 |
(2.2) |
avec 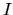 l'identité et
l'identité et
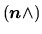 la matrice qui du produit vectoriel par
la matrice qui du produit vectoriel par  (voir équation
(voir équation ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
Le problème inverse est de trouver l'axe  et l'angle
et l'angle 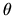 d'après la matrice
d'après la matrice  . Il n'y a pas de solution unique (angle défini à
. Il n'y a pas de solution unique (angle défini à 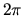 près, axe ou son opposé). On peut en trouver une en remarquant que
près, axe ou son opposé). On peut en trouver une en remarquant que
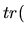

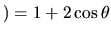 et que
et que

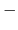

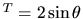
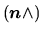
Soit une base
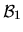 tournée de
tournée de

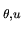 par rapport à une base de référence
par rapport à une base de référence
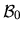 . Nous voulons lui appliquer une rotation supplémentaire, par exemple
. Nous voulons lui appliquer une rotation supplémentaire, par exemple

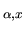 d'angle
d'angle 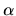 suivant l'axe
suivant l'axe  . Pour calculer sa nouvelle matrice d'orientation il est important de savoir de quel axe
. Pour calculer sa nouvelle matrice d'orientation il est important de savoir de quel axe  on parle:
on parle:
- s'il s'agit de l'axe
 de la base
de la base
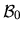 , alors on multiplie à gauche et la nouvelle matrice de rotation vaut
, alors on multiplie à gauche et la nouvelle matrice de rotation vaut

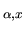

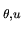
- s'il s'agit de l'axe
 de la base
de la base
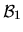 , alors on multiplie à droite et la nouvelle matrice de rotation vaut
, alors on multiplie à droite et la nouvelle matrice de rotation vaut

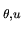

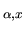
Les angles d'Euler consistent à appliquer trois rotations successives selon des axes principaux. Suivant le contexte, on les interprète comme des rotations suivant les axes d'une base de référence, ou suivant les axes des bases intermédiaires successives.
Par exemple, la rotation

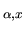

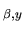

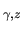 (matrices définies en éq.
(matrices définies en éq. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) peut s'interpêter de deux manières mathématiquement équivalentes mais intuitivement différentes:
) peut s'interpêter de deux manières mathématiquement équivalentes mais intuitivement différentes:
- rotation d'angle
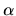 selon
selon  (de
(de
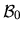 ) puis rotation d'angle
) puis rotation d'angle 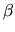 autour du nouveau
autour du nouveau 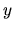 (ayant subi une rotation) puis rotation d'angle
(ayant subi une rotation) puis rotation d'angle 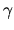 autour du nouveau
autour du nouveau 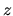 (ayant subi deux rotations)
(ayant subi deux rotations)
- ou rotation d'angle
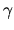 autour de
autour de 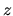 de
de
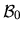 puis rotation d'angle
puis rotation d'angle 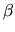 autour de
autour de 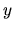 de
de
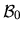 puis rotation d'angle
puis rotation d'angle 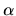 selon
selon  de
de
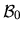 .
.
Les angles d'Euler présentent toutefois certains inconvénients:
- non-unicité: par exemple en xyz, la rotation
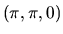 est équivalente à
est équivalente à 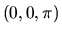
- perte d'un degré de liberté: par exemple pour
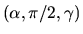 en xyz,
en xyz, 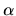 et
et 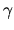 ont le même effet car ils font pivoter autour d'un même axe. Aucune rotation n'est alors possible autour du troisième axe. Ceci représente le cas extrème, mais toute configuration proche de celle-ci posera des problèmes numériques
ont le même effet car ils font pivoter autour d'un même axe. Aucune rotation n'est alors possible autour du troisième axe. Ceci représente le cas extrème, mais toute configuration proche de celle-ci posera des problèmes numériques
- les interpolations peuvent prendre des chmeins compliqués ou inattendus.
Extension des nombres complexes:
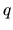
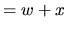
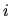
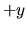
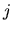
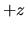
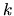
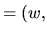

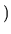 .
.
w est la partie réelle,  la partie imaginaire.
Propriétés de
la partie imaginaire.
Propriétés de 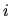 ,
, 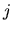 ,
, 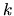 :
Vecteur 3D:
Produit de quaternions (non commutatif):
Quaternion conjugué:
Quaternions unitaires, utilisés pour représenter les rotations:
Rotation
:
Vecteur 3D:
Produit de quaternions (non commutatif):
Quaternion conjugué:
Quaternions unitaires, utilisés pour représenter les rotations:
Rotation
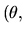

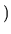 : (
: (

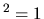 )
Rotation d'un vecteur
)
Rotation d'un vecteur 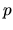 :
:

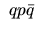
Matrice de rotation associée à un quaternion unitaire:
Composition des rotations:
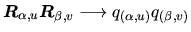
Rotation inverse:
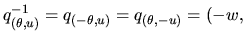

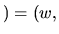
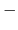
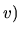
Conversion
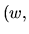

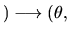

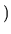 :
:
Soit une base initialement définie par
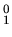
 à
à 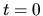 , que nous voulons faire évoluer continument vers
, que nous voulons faire évoluer continument vers
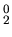

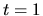 .
.
- On ne peut interpoler simplement les coefficients d'une matrice de rotation car on viole alors les contraintes sur les vecteurs-colonnes (unitaires, orthogonaux).
- On peut interpoler les angles d'Euler mais le chemin emprunté sera rarement le plus direct, et la vitesse rarement constante.
Il convient de:
- calculer la matrice de passage de la configuration initiale à la configuration finale:
- calculer angle et axe
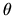 ,
, 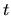 els que:
els que:
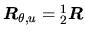
- interpoler en appliquant
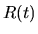

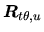
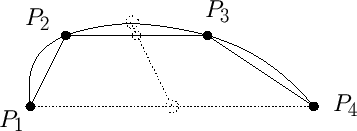
Nous voulons passer de manière lisse par différentes orientations au cours du temps. Nous nous basons sur la méthode d'approximation itérative des splines présentée en figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png)
Figure:
Approximation itérative d'une spline. Un nouveau point est calculé par somme pondérée des points
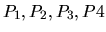 ayant respecivement pour coefficients
ayant respecivement pour coefficients
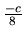 ,
,
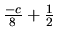 , ,
, ,
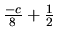 , et
, et
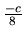 . Le coefficient
. Le coefficient 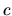 exprime la continuité de la spline et peut être fixé à 1.
exprime la continuité de la spline et peut être fixé à 1.
 |
et construisons une analogie entre vecteurs de
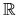
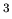 et quaternions unitaires:
et quaternions unitaires:
| |
vecteur v |
quaternion
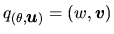 |
| composition |
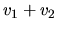 ( (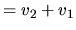 ) ) |
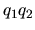 ( (
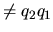 !) !) |
| inverse |
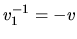 |
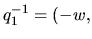  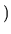 |
| produit avec un scalaire |
k v |
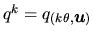 |
| distance |
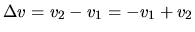 |
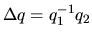 |
| interpolation |
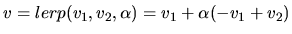 |
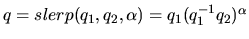 |
| moyenne |
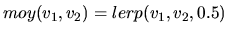 |
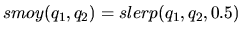 |
Nous pouvons maintenant à partir de quatre quaternions en générer un supplémentaire, et à partir de 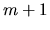 quaternions en obtenir
quaternions en obtenir 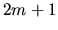 :
:
A COMPLETER
Considérons un vecteur

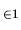 , fixe dans un repère
, fixe dans un repère
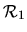 . Le repère
. Le repère
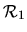 est en rotation par rapport à un repère
est en rotation par rapport à un repère
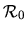 . Nous nous intéressons à la projection
. Nous nous intéressons à la projection
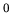
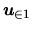 de ce vecteur dans
de ce vecteur dans
 , que nous appellerons parfois
, que nous appellerons parfois  pour simplifier, et à sa dérivée dans
pour simplifier, et à sa dérivée dans
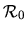 que nous noterons
que nous noterons
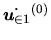 .
.
Soit 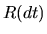 la rotation subie par
la rotation subie par
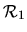 entre l'instant
entre l'instant 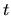 et l'instant
et l'instant 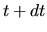 . Nous pouvons écrire:
. Nous pouvons écrire:
Soit
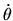 la vitesse angulaire autour de l'axe de rotation, que nous choisissons égal à
la vitesse angulaire autour de l'axe de rotation, que nous choisissons égal à 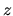 pour simplifier. Nous obtenons par un développement limité à l'ordre 1:
où
pour simplifier. Nous obtenons par un développement limité à l'ordre 1:
où
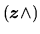 est l'opérateur matriciel de produit vectoriel par
est l'opérateur matriciel de produit vectoriel par 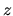 . Cette formule peut s'étendre par changement de base à n'importe quel axe de rotation
. Cette formule peut s'étendre par changement de base à n'importe quel axe de rotation  (unitaire). Posons
(unitaire). Posons
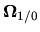
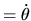
 . En divisant l'expression
. En divisant l'expression ![[*]](file:/usr/lib/latex2html/icons/crossref.png) par
par 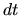 et en faisant tendre
et en faisant tendre 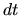 vers 0 nous obtenons
vers 0 nous obtenons
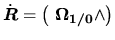 .
.
Nous pouvons écrire la dérivée temporelle dans
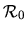 :
:
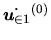

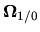
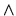
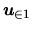 , ou en simplifiant la notation:
, ou en simplifiant la notation:
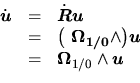 |
(3.3) |
Considérons la vitesse dans
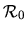 d'un point
d'un point  fixe dans
fixe dans
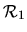 en mouvement par rapport à
en mouvement par rapport à
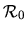 . Soient
. Soient 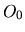 l'origine de
l'origine de
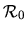 et
et 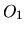 l'origine de
l'origine de
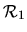 . Nous dérivons en coordonnées homogènes la projection de
. Nous dérivons en coordonnées homogènes la projection de  dans
dans
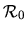 :
:
Nous appelons
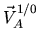 vitesse de
vitesse de  fixe dans
fixe dans
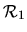 par rapport à
par rapport à
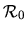 . On peut noter que
. On peut noter que
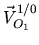
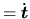 . Nous en déduisons les relations du champ des vitesses d'un solide:
. Nous en déduisons les relations du champ des vitesses d'un solide:
la dernière relation se deduisant trivialement par soustraction
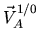
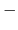
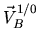 .
.
En dérivant la relation ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , et sachant que
, et sachant que
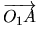 est fixe dans
est fixe dans
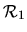 , nous obtenons la relation du champ des accélerations d'un solide:
, nous obtenons la relation du champ des accélerations d'un solide:
Soit
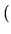
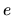
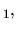
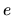
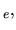
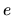
 une base de
une base de
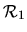 . Nous pouvons écrire:
. Nous pouvons écrire:
d'où:
Soit
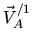 la vitesse d'un point
la vitesse d'un point  dans le repère
dans le repère
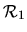 . Celle-ci vient s'ajouter à la vitesse qu'aurait le point s'il était fixe dans
. Celle-ci vient s'ajouter à la vitesse qu'aurait le point s'il était fixe dans
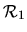 . Nous avons donc:
. Nous avons donc:
Notons que le point 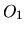 étant l'origine du repère
étant l'origine du repère
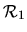 , on a
, on a
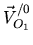

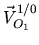 .
En dérivant la relation
.
En dérivant la relation ![[*]](file:/usr/lib/latex2html/icons/crossref.png) nous obtenons:
ou encore:
nous obtenons:
ou encore:
avec:
-
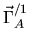
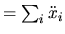
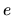
 accéleration relative
accéleration relative
-
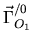 accéleration d'entraînement
accéleration d'entraînement
-
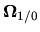
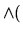
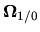
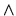
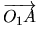
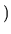 accéleration centripète
accéleration centripète
-
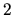
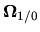
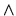
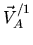 accéleration de Coriolis
accéleration de Coriolis
Si nous appliquons la relation ![[*]](file:/usr/lib/latex2html/icons/crossref.png) à un point fixe dans un repère
à un point fixe dans un repère
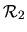 , nous pouvons directement écrire
, nous pouvons directement écrire
et plus généralement:
La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) illustre une application de cette formule. La vitesse
illustre une application de cette formule. La vitesse
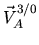 est la somme des contributions de chaque mouvement relatif. On note que la vitesse dûe à une rotation est perpendiculaire à la droite joignant le point au centre de rotation. La vitesse de translation est reportée tel quel.
est la somme des contributions de chaque mouvement relatif. On note que la vitesse dûe à une rotation est perpendiculaire à la droite joignant le point au centre de rotation. La vitesse de translation est reportée tel quel.
Figure:
Composition des vitesses.
|
Les liaisons cinématiques définissent les mouvements possibles entre deux solides parmi les trois translations et trois rotations possibles. Les liaisons se caractérisent par leurs degrés de liberté (ddl). La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) montre l'exemple de la liaison pivot glissant, qui autorise deux degrés de liberté: un en translation et un en rotation. La plus contrainte est la liaison encastrement, avec zéro ddl, la plus libre est la liaison libre avec six ddl. Les principales liaisons sont présentées en annexe
montre l'exemple de la liaison pivot glissant, qui autorise deux degrés de liberté: un en translation et un en rotation. La plus contrainte est la liaison encastrement, avec zéro ddl, la plus libre est la liaison libre avec six ddl. Les principales liaisons sont présentées en annexe ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Figure:
Liaison pivot glissant (images de Roger Bouisset). De haut en bas et de gauche à droite: des surfaces pouvant créer ce type de liaison, les axes principaux de la liaison, la représentation normalisée de la liaison, les mouvements relatifs possibles.
|
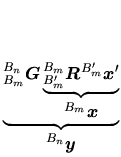
Une liaison permet le mouvement relatif de deux repères qui dans le cas géneral ne sont pas directement les repères principaux des solides.
La transformation
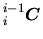 de
de
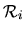 vers
vers
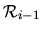 dûe à une liaison peut se décomposer en trois transformations:
dûe à une liaison peut se décomposer en trois transformations:
comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Figure:
Une liaison entre les repères i et i+1, avec ses repères intermédiaires.
|
La matrice
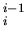
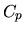 traduit la position de la liaison par rapport à
traduit la position de la liaison par rapport à
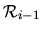 . La matrice
. La matrice
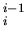
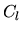 traduit le deplacement dans la liaison, par rapport à une position de référence. Elle peut varier avec le temps et conformement aux ddl. La matrice
traduit le deplacement dans la liaison, par rapport à une position de référence. Elle peut varier avec le temps et conformement aux ddl. La matrice
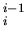
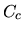 (plus précisement, son inverse) traduit la position de la liaison par rapport à
(plus précisement, son inverse) traduit la position de la liaison par rapport à
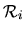 .
.
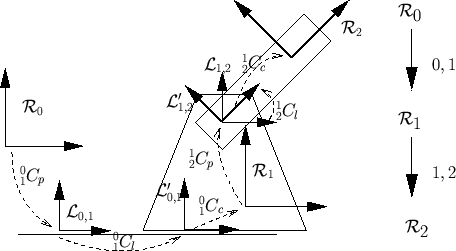
La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) présente un exemple de chaîne articulée. Un socle mobile de repère
présente un exemple de chaîne articulée. Un socle mobile de repère
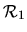 peut se déplacer sur le sol de repère
peut se déplacer sur le sol de repère
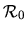 . Un bras de repère
. Un bras de repère
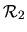 est articulé par rapport au socle mobile. À doite de la figure, le graphe cinématique représente l'accrochage des solides (noeuds) par les liaisons (arcs). Ce graphe est orienté en partant du repère absolu, qui est toujours à la racine.
est articulé par rapport au socle mobile. À doite de la figure, le graphe cinématique représente l'accrochage des solides (noeuds) par les liaisons (arcs). Ce graphe est orienté en partant du repère absolu, qui est toujours à la racine.
Figure:
Corps articulés et graphes cinématiques. À gauche, un mécanisme avec ses solides, liaisons et repères intermédiaires. Au centre, le graphe cinématique correspondant. À droite, un graphe cinématique plus complexe.
|
3.2.2.2 Modèle de Denavit-Hartenberg
La notation de Denavit-Hartenberg, très utilisée en robotique, correspond â un cas simplifié:
- le repère du solide enfant est centré sur le repère mobile de l'articulation:
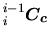

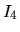
- les liaisons n'autorisent qu'un degré de liberté en translation et en rotation, le long du même axe (
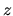 par convention).
par convention).
De plus, l'axe 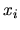 d'un repère
d'un repère
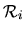 est par définition confondu avc la perpendiculaire commune aux axes
est par définition confondu avc la perpendiculaire commune aux axes
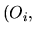
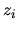
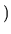 et
et
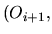
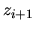
 . La figure
. La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) illustre la mise en position d'un repère par rapport à son père.
illustre la mise en position d'un repère par rapport à son père.
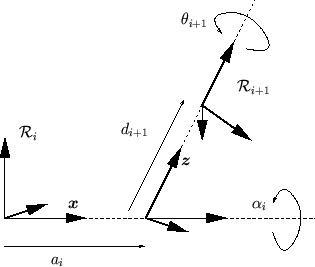
Figure:
Liaison selon Denavit-Hartenberg. Quatre paramètres décrivent la position du fils (i+1) par rapport au pére (i).
|
Pour aller du repère père
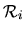 au repère fils
au repère fils
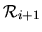 , on translate selon
, on translate selon  (paramètre
(paramètre 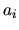 ), puis on tourne selon
), puis on tourne selon  (paramètre
(paramètre 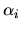 ), puis on translate selon
), puis on translate selon 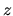 (paramètre
(paramètre 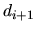 ) et finalement on pivote selon
) et finalement on pivote selon 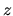 (paramètre
(paramètre
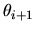 ). Les paramètres
). Les paramètres 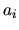 et
et 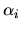 sont constants, les deux autres correspondant à la rotation et la translation selon l'axe. La transformation géometrique vaut:
sont constants, les deux autres correspondant à la rotation et la translation selon l'axe. La transformation géometrique vaut:
Notez que nous numérotons les repères en partant du repère absolu
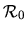 . Il arrive de recontrer l'ordre inverse, particulièrement dans la littérature robotique.
. Il arrive de recontrer l'ordre inverse, particulièrement dans la littérature robotique.
À chaque ddl 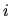 est associé un axe
est associé un axe

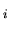 (vecteur unitaire), une valeur de position
(vecteur unitaire), une valeur de position 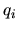 et une valeur de vitesse
et une valeur de vitesse 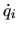 . Les valeurs aux ddl définissent la position d'une liaison. En translation, ces valeurs sont reportées dans le vecteur translation de la matrice de passage. Le cas des rotations est plus complexe. Pour les liaisons à un ou deux ddl, on utilise les angles d'Euler et on calcule la matrice correspondante. Pour les liaisons à trois ddl et mouvements de grande amplitude, on ne peut employer les angles d'Euler à cause des limitations analytiques de ceux-ci, notamment la perte d'un ddl dans certaines configurations. On a alors recours aux quaternions, ou directement aux matrices. Le paramétrage par angles d'Euler reste possible pour exprimer des petites variations autour de la position courante.
. Les valeurs aux ddl définissent la position d'une liaison. En translation, ces valeurs sont reportées dans le vecteur translation de la matrice de passage. Le cas des rotations est plus complexe. Pour les liaisons à un ou deux ddl, on utilise les angles d'Euler et on calcule la matrice correspondante. Pour les liaisons à trois ddl et mouvements de grande amplitude, on ne peut employer les angles d'Euler à cause des limitations analytiques de ceux-ci, notamment la perte d'un ddl dans certaines configurations. On a alors recours aux quaternions, ou directement aux matrices. Le paramétrage par angles d'Euler reste possible pour exprimer des petites variations autour de la position courante.
On peut rassembler l'ensemble des valeurs associées aux ddl dans un vecteur 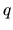 qui définit l'état du sytème. L'ensemble des états possibles est appelé espace articulaire du système. De même on peut regrouper les vitesses articulaires dans un vecteur
qui définit l'état du sytème. L'ensemble des états possibles est appelé espace articulaire du système. De même on peut regrouper les vitesses articulaires dans un vecteur
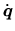 .
.
La cinematique dite directe consiste à calculer des positions et vitesses dans l'espace cartésien â partir de l'état articulaire du système. Dans cette partie nous considèrerons un mécanisme modélisé par la notation de Denavit-Hartenberg (cf. section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), constitué d'une chaîne cinématique dont les solides sont numérotés de 0 (repère absolu) à n. Le repère fils est translaté et tourné selon l'axe
), constitué d'une chaîne cinématique dont les solides sont numérotés de 0 (repère absolu) à n. Le repère fils est translaté et tourné selon l'axe  du père, puis translaté et tourné selon le nouvel axe
du père, puis translaté et tourné selon le nouvel axe 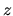 .
.
La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) présente un algorithme de calcul des matrices de passage de chaque solide de la chaîne.
présente un algorithme de calcul des matrices de passage de chaque solide de la chaîne.
Figure:
Calcul des matrices de positions dans le formalisme de Denavit-Hartenberg.
|
La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) présente un algorithme de calcul de vitesses. Les données sont:
présente un algorithme de calcul de vitesses. Les données sont:
- la position
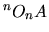 d'un point A dans le repère
d'un point A dans le repère
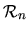
- les positions
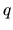 et vitesses articulaires
et vitesses articulaires
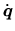
Les résultats sont:
- la position
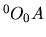 de A dans le repère absolu
de A dans le repère absolu
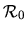
- la vitesse de rotation
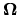
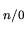
- la vitesse
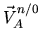 de A fixe dans
de A fixe dans
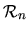 par rapport à
par rapport à
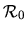 , exprimée dans
, exprimée dans
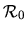
Au passage, toutes les matrices
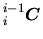 sont calculées.
sont calculées.
Figure:
Calcul de vitesse dans le formalisme de Denavit-Hartenberg.
|
Problématique: trouver des configurations articulaires pour satisfaire des contraintes définies dans l'espace cartésien.
Considérons un mécanisme comportant deux liaisons glissière alignées sur les axes du repère absolu, comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Chaque degré de liberté est caractérisé par son axe
. Chaque degré de liberté est caractérisé par son axe 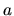 et sa coordonnée articulaire
et sa coordonnée articulaire 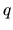 . L'axe portant
. L'axe portant
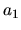 est fixe tandis que l'axe portant
est fixe tandis que l'axe portant 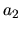 se translate.
se translate.
Figure:
Un mécanisme à axes orthogonaux.
|
Nous désirons amener le point 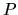 jusqu'à la position
jusqu'à la position 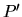 et pour cela nous devons satisfaire une contrainte de déplacement
et pour cela nous devons satisfaire une contrainte de déplacement
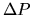

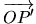
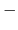
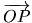

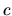
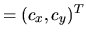 au moyen d'un déplacement articulaire
au moyen d'un déplacement articulaire
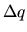
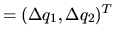 . Dans ce cas simple la reponse est évidemment
. Dans ce cas simple la reponse est évidemment
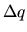
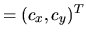 .
.
Considérons maintenant un mécanisme similaire, mais à axes quelconques, comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Figure:
Un mécanisme à axes non orthogonaux.
|
La résolution d'une contrainte de déplacement nécessite de poser et résoudre un système d'équations linéaires:
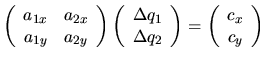 |
(4.1) |
Considérons maintenant la contrainte suivante: le point 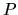 doit se positionner sur la droite définie par un point
doit se positionner sur la droite définie par un point 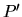 et un vecteur normal
et un vecteur normal

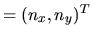 , comme illustré sur la figure
, comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Nous sommes en présence d'une contrainte scalaire, puisqu'on peut l'exprimer par une équation unique
. Nous sommes en présence d'une contrainte scalaire, puisqu'on peut l'exprimer par une équation unique
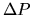



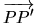

 .
.
Figure:
Une contrainte scalaire appliquée au mécanisme 2D: rejoindre une droite.
|
Posons, développons et regroupons l'équation sur le déplacement:
Chaque contrainte scalaire correspond à une ligne d'un sytème d'équation. Une contrainte au sens général peut être vue comme un ensemble de contraintes scalaires. Par exemple, nous pouvons écrire l'équation ![[*]](file:/usr/lib/latex2html/icons/crossref.png) comme:
Nous avons une équation à deux inconnues, ce qui dans le cas géneral fournit un espace de solutions de dimension 1. Plus généralement, pour un système de
comme:
Nous avons une équation à deux inconnues, ce qui dans le cas géneral fournit un espace de solutions de dimension 1. Plus généralement, pour un système de  équations a
équations a 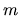 inconnues, on peut s'attendre à un espace de solutions de dimension
inconnues, on peut s'attendre à un espace de solutions de dimension 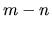 . Toutefois, les systèmes peuvent présenter des "déficiences de rang" quand une colonne de la matrice est combinaison linéaire des autres. Le mécanisme sur la figure
. Toutefois, les systèmes peuvent présenter des "déficiences de rang" quand une colonne de la matrice est combinaison linéaire des autres. Le mécanisme sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) a beau posséder trois degrés de liberté, ils sont tous dans le plan
a beau posséder trois degrés de liberté, ils sont tous dans le plan
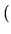

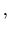
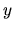
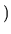 et il ne pourra jamais satisfaire une contrainte en
et il ne pourra jamais satisfaire une contrainte en 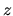 . Par contre, la dimension de l'espace des solutions dans le plan augmente de 1.
. Par contre, la dimension de l'espace des solutions dans le plan augmente de 1.
Figure:
Mécanisme redondant. Les trois degrés de liberté dans le plan augmentent la dimension de l'espace des solutions. Ce mécanisme ne peut cependant pas satisfaire de contraintes dans la direction z.
|
Les degrés de liberté en rotation induisent des fonctions trigonométriques dans les équations géométriques, rendant celles-ci non linéaires. On en voit quelques conséquences sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Il y a deux manières de mener le point
. Il y a deux manières de mener le point 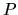 au point
au point 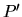 , mais aucune d'atteindre
, mais aucune d'atteindre 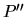 qui est trop loin.
qui est trop loin.
Figure:
Un mécanisme avec rotations. Un même type de contrainte peut avoir une, plusieurs ou aucune solution.
|
L'équation de cinématique du solide (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) nous donne, en remarquant que
) nous donne, en remarquant que
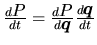 :
:
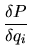 |
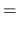 |
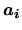 (ddl en translation) (ddl en translation) |
(4.2) |
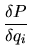 |
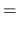 |
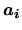 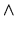 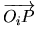 (ddl en rotation) (ddl en rotation) |
(4.3) |
Autrement dit, les variations de coordonnées articulaires en translation se répercutent tel quel sur tout point; le cas des rotations est illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , où la variation est orthogonale à la droite menant à l'axe de rotation pour des (infiniment) petites variations d'angle.
, où la variation est orthogonale à la droite menant à l'axe de rotation pour des (infiniment) petites variations d'angle.
Figure:
Effet d'une petite rotation.
|
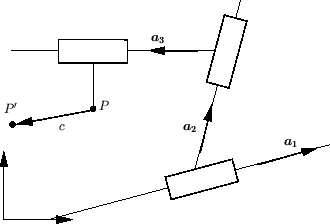
Nous considérons la position d'un point 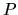 influencée par des ddl numerotés de
influencée par des ddl numerotés de 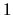 à
à  .
Nous pouvons regrouper toutes les dérivées partielles en colonnes dans une matrice appelée matrice jacobienne de vitesse (ou de petit déplacement) au point
.
Nous pouvons regrouper toutes les dérivées partielles en colonnes dans une matrice appelée matrice jacobienne de vitesse (ou de petit déplacement) au point 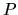 :
:
de dimensions 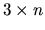 et qui permet d'approximer:
et qui permet d'approximer:
Cette formule est exacte si tous les ddl sont des translations.
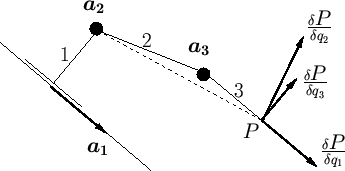
La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) illustre les vecteurs-colonnes de la matrice
illustre les vecteurs-colonnes de la matrice
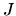
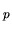 sur un exemple de mécanisme.
sur un exemple de mécanisme.
Figure:
Les vecteurs colonnes de la jacobienne des vitesses du point P. Les vecteurs orthogonaux au plan de la figure sont illustrés par un disque plein.
|
Les contraintes scalaires du type
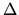
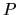


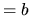 se traduisent par une équation:
se traduisent par une équation:
Similairement à la position d'un point, la variation d'orientation d'un repère peut se représenter sous forme linéaire:
La quantité 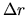 est colinéaire à l'axe de rotation et a pour norme l'angle de rotation:
est colinéaire à l'axe de rotation et a pour norme l'angle de rotation:
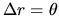
 correspond à une rotation d'axe
correspond à une rotation d'axe  et d'angle
et d'angle 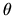 . Les ddl en rotation influent directement sur l'orientation, tandis que les ddl en translation n'ont pas d'influence. Nous avons donc:
. Les ddl en rotation influent directement sur l'orientation, tandis que les ddl en translation n'ont pas d'influence. Nous avons donc:
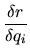 |
 |
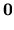 (ddl en translation) (ddl en translation) |
(4.5) |
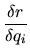 |
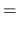 |
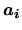 (ddl en rotation) (ddl en rotation) |
(4.6) |
Nous considérons l'orientation d'un repère influencée par des ddl numerotés de 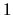 à
à  .
La jacobienne d'orientation est:
.
La jacobienne d'orientation est:
Soit
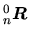 la matrice d'orientation du repère considéré. Nous voulons l'amener à une orientation
la matrice d'orientation du repère considéré. Nous voulons l'amener à une orientation
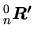 au moyen d'une rotation
au moyen d'une rotation

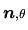 telle que:
telle que:
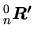


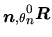 . Pour appliquer cette rotation au moyen des ddl disponibles nous resolvons donc:
Notez que cette solution n'est juste que pour les rotations inifiniment petites, car elle ne tient pas compte de la non-commutativité des rotations.
. Pour appliquer cette rotation au moyen des ddl disponibles nous resolvons donc:
Notez que cette solution n'est juste que pour les rotations inifiniment petites, car elle ne tient pas compte de la non-commutativité des rotations.
Exemple d'application: orientation d'une caméra.
Nous désirons rendre un vecteur  colinéaire à un vecteur
colinéaire à un vecteur 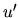 comme illustré sur la figure
comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Figure:
Alignement d'un vecteur sur un autre.
|
La rotation la plus directe transformant  en
en 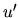 a son axe orthogonal à
a son axe orthogonal à  et
et 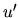 , et pour angle l'angle
, et pour angle l'angle 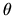 entre ces deux vecteurs. L'alignement entre les deux vecteurs nous laissant un degré de liberté, nous pourrions appliquer ensuite une rotation arbitraire autour de
entre ces deux vecteurs. L'alignement entre les deux vecteurs nous laissant un degré de liberté, nous pourrions appliquer ensuite une rotation arbitraire autour de 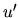 . La rotation autour de
. La rotation autour de  , orthogonal à
, orthogonal à  et
et  , doit quant à elle être nulle. L'alignement de
, doit quant à elle être nulle. L'alignement de  sur
sur  nécessite donc de poser les équations:
nécessite donc de poser les équations:
Exemple d'application: orientation d'un axe de perceuse.
4.3 Résolution des équations linéaires
Soit
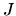
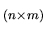
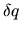
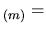
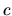
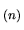 le système de
le système de  équations et
équations et 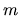 inconnues à résoudre. Nous considérons une matrice sans déficience de rang, sachant qu'une déficience entraîne une diminution du nombre d'inconnues indépendantes.
inconnues à résoudre. Nous considérons une matrice sans déficience de rang, sachant qu'une déficience entraîne une diminution du nombre d'inconnues indépendantes.
Si 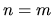 et sous les hypothèses établies, le système a une solution unique. Il peut se résoudre par la factorisation LU de
et sous les hypothèses établies, le système a une solution unique. Il peut se résoudre par la factorisation LU de 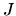 .
.
Dans ce cas le système a une infinité de solutions. La pseudo-inverse de 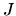 , notée
, notée
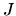
 , nous permet d'en calculer une:
, nous permet d'en calculer une:
Cette solution minimise
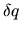
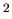 parmi toutes les solutions.
parmi toutes les solutions.
Dans ce cas on doit trouver un compromis. Une autre formule de pseudo-inverse de 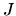 nous permet d'en calculer un:
nous permet d'en calculer un:
Cette solution minimise
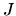
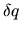
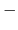
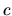
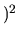 .
.
Certains mécanismes peuvent présenter des configurations spéciales appelées singularités, dans lesquelles des colonnes de la matrice Jacobienne se retrouvent linéairement dépendantes. La méthode de résolution employée jusqu'alors peut échouer.
Ces cas se traitent, soit en appliquant une légère perturbation au système pour l'éloigner de la singularité, soit en appliquant une méthode de résolution plus perfectionnée comme celle présentée en section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
4.3.5 Décomposition en valeurs singulières (SVD)
Les méthodes précédentes peuvent échouer, quand par exemple une matrice 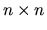 est de rang
est de rang 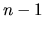 , auquel cas aucune inverse ni pseudo-inverse ne peut être calculée. Ces cas se produisent lors de singularités, ou pour certains mécanismes redondants.
On peut alors utiliser la décomposition SVD:
La matrice
, auquel cas aucune inverse ni pseudo-inverse ne peut être calculée. Ces cas se produisent lors de singularités, ou pour certains mécanismes redondants.
On peut alors utiliser la décomposition SVD:
La matrice 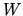 est diagonale et contient des valeurs positives appelées valeurs singulières. Les matrices
est diagonale et contient des valeurs positives appelées valeurs singulières. Les matrices 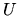 et
et 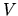 sont orthogonales.
Les vecteurs-colonnes de
sont orthogonales.
Les vecteurs-colonnes de 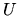 associés à une valeur singulière non nulle constituent une base de l'image de
associés à une valeur singulière non nulle constituent une base de l'image de 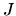 . Les vecteurs-colonnes de
. Les vecteurs-colonnes de 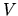 associés à une valeur singulière nulle constituent une base du noyau de
associés à une valeur singulière nulle constituent une base du noyau de 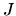 .
La solution du système est:
où
.
La solution du système est:
où
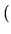
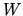
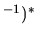 est une matrice diagonale composée des inverses des valeurs singulières non nulles, et de 0 pour les valeurs singulières nulles.
est une matrice diagonale composée des inverses des valeurs singulières non nulles, et de 0 pour les valeurs singulières nulles.
Pour plus d'inconnues que d'équations la solution minimise
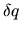
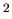 , dans le cas contraire elle minimise
, dans le cas contraire elle minimise
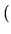
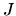
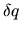
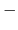
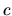
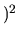 .
.
La décomposition SVD est hélas un algorithme très coûteux.
Dans le cas d'équations non linéaires, la résolution des équations linéaires à l'aide du jacobien ne nous donne qu'une solution approchée. Il convient donc de réitérer le processus. La figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) présente l'algorithme itératif de base.
présente l'algorithme itératif de base.
Figure:
Algorithme itératif de base pour la résolution d'équations géométriques.
|
Aux alentours des singularités cet algorithme peut présenter un comportement d'oscillation autour de la solution. On peut résoudre ce problème en remplaçant l'instruction
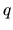
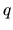
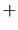
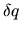 par un algorithme de minimisation de
par un algorithme de minimisation de
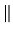
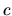
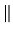 sur la droite passant par
sur la droite passant par 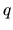 et de direction
et de direction 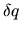 . Cette idée est exploitée dans les algorithmes les plus performants ("quasi-Newton", ou à base de gradient conjugué).
. Cette idée est exploitée dans les algorithmes les plus performants ("quasi-Newton", ou à base de gradient conjugué).
Les mécanismes sont souvent pourvus de butées qui empêchent les coordonnées articulaires de dépasser certaines valeurs. On peut adapter l'algorithme précédent pour qu'en cas de depassement, la valeur soit fixée à la valeur limite. Dans ce cas le ddl correspondant n'est plus libre et la résolution doit se poursuivre aux moyens des autres ddl. L'algorithme présenté en figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) applique cette idée.
applique cette idée.
Figure:
Algorithme itératif avec prise en compte de butées articulaires.
|
Cet algorithme n'est pas garanti de converger vers la solution dans les cas complexes. Il convient alors de le redémarrer en partant de la solution courante et en libérant tous les ddl.
Nous nous plaçons dans le cas où les ddl fournissent un espace de solutions appelé espace libre. On peut remarquer que
L'opérateur
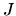
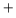
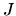
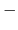
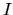 projette les vecteurs de corrdonnées articulaires sur le noyau de
projette les vecteurs de corrdonnées articulaires sur le noyau de 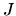 . Il en résulte que
. Il en résulte que
Quand les ddl fournissent un espace de solutions, il peut être souhaitable d'y optimiser certains critères. Pour un personnage articulé, on peut par exemple souhaiter que les coordonnées articulaires soient le plus proche possible de valeurs de référence représentant une position "naturelle". On formule alors un coût 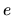 à minimiser:
à minimiser:
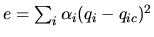 . Le problème se formule mathématiquement par: minimiser
. Le problème se formule mathématiquement par: minimiser 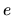 sous la contrainte
sous la contrainte 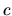 . Il existe des algorithmes perfectionnés pour résoudre ce genre de problèmes. Toutefois, il existe une approche rudimentaire, présentée en figure
. Il existe des algorithmes perfectionnés pour résoudre ce genre de problèmes. Toutefois, il existe une approche rudimentaire, présentée en figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , qui peut donner de bons résultats. La difficulté est de définir ce qu'on entend par "petit" pas.
, qui peut donner de bons résultats. La difficulté est de définir ce qu'on entend par "petit" pas.
Figure:
Une approche simple pour minimiser un critère e tout en respectant des contraintes.
|
Une autre application de l'optimisation de pose consiste à contrôler le centre de gravité d'un personnage afin que sa projection au sol soit située entre les pieds.
A. Liaisons cinématiques
| Liaison ponctuelle |
|
|
| Liaison pivot |
|
|
| Liaison glissière |
|
|
| Liaison pivot glissant |
|
|
| Liaison sphérique |
|
|
| Appui plan |
|
|
| Linéaire rectiligne |
|
|
| Linéaire annulaire |
|
|
| Hélicoidale |
|
|
| application de A vers B |
mapping from A to B |
| base |
basis |
| degré de liberté |
degree of freedom |
| espace vectoriel |
vector space |
| liaison cinématique |
kinematic joint |
| liaison appui plan |
flat joint |
| liaison glissière |
prismatic joint |
| liaison pivot |
revolute joint (pin joint) |
| liaison pivot glissant |
cylindrical joint |
| liaison rotule |
spherical joint |
| produit scalaire |
dot product |
produit vectoriel
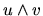 |
cross product
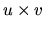 |
| repère |
frame, coordinate system |
| valeur propre |
eigenvalue |
| vecteur propre |
eigenvector |
| vecteur unitaire |
unit vector |
- 1
-
Press, Teukolski, Vetterling, and Flannery.
Numerical Recipes in C.
Cambridge University Press, 1992.



Francois Faure
2002-10-30
![]() ) alors le groupe est dit commutatif.
) alors le groupe est dit commutatif.
![]() est une sous-ensemble de
est une sous-ensemble de
![]() stable par combinaison lineaire.
stable par combinaison lineaire.
![]()
![]() .
.
![]() : L'ensemble des combinaisons linéaires des vecteurs de A.
: L'ensemble des combinaisons linéaires des vecteurs de A.
![]() et
et
![]() de
de
![]() :
:
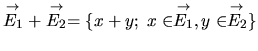 .
La somme de deux SEV est un SEV. L'intersection aussi. Si l'intersection de deux SEV est nulle, la somme est dite directe et notée
.
La somme de deux SEV est un SEV. L'intersection aussi. Si l'intersection de deux SEV est nulle, la somme est dite directe et notée
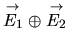
![]()
![]() : la somme de deux droites vectorielles distinctes est directe et c'est un plan vectoriel.
: la somme de deux droites vectorielles distinctes est directe et c'est un plan vectoriel.
![]()
![]() de vecteurs de
de vecteurs de
![]() tel que pour tout élément x de
tel que pour tout élément x de
![]() il existe une decomposition unique
il existe une decomposition unique
![]()
![]() ).
).
![]() ).
).
![]() si:
si:
![]() est la dimension (finie) d'un EV et
est la dimension (finie) d'un EV et
![]()
![]()
![]() une base, on peut définir un vecteur
une base, on peut définir un vecteur
![]()
![]()
![]() par ses composantes dans la base:
par ses composantes dans la base:
![]()
![]()
![]() et
et
![]() sont deux SEV de
sont deux SEV de
![]() tels que
tels que
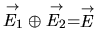 alors la dimension de
alors la dimension de
![]() est appelée codimension de
est appelée codimension de
![]() , et réciproquement.
, et réciproquement.
![]()
![]() , la codimension d'une droite est 2, la codimension d'un plan est 1.
, la codimension d'une droite est 2, la codimension d'un plan est 1.
![]() de
de
![]() . On dit que
. On dit que
![]() est la direction de F.
est la direction de F.
![]() où
où ![]() est un point de E et
est un point de E et ![]() une base de
une base de
![]() . Pour tout point
. Pour tout point ![]() de E,
de E,
![]()
![]() .
.
![]() ,
,
![]() etc.
etc.
![]() et
et
![]() sont des SEV orthogonaux si tout élément de l'un est orthogonal a tout élement de l'autre.
sont des SEV orthogonaux si tout élément de l'un est orthogonal a tout élement de l'autre.
![]()
![]() et tout vecteur
et tout vecteur ![]() on a:
on a:
![]() de deux applications linéaires est l'application qui à
de deux applications linéaires est l'application qui à ![]() associe
associe ![]() .
La composée de deux AL est une AL.
.
La composée de deux AL est une AL.
![]() d'un EV
d'un EV
![]() est un sous-espace vectoriel formé des transformees des élements de
est un sous-espace vectoriel formé des transformees des élements de
![]() .
.
![]()
![]() , une projection sur un plan a pour image ce plan.
, une projection sur un plan a pour image ce plan.
![]() par une AL de
par une AL de
![]() dans
dans
![]() est l'ensemble des élements de
est l'ensemble des élements de
![]() se transformant en éléments de
se transformant en éléments de
![]() . C'est un SEV de
. C'est un SEV de
![]() .
.
![]() de
de
![]() dans
dans
![]() , noté
, noté ![]() , est l'image réciproque de l'élément nul de
, est l'image réciproque de l'élément nul de
![]() Exemple: dans
Exemple: dans
![]()
![]() , le noyau d'une projection sur un plan est la droite dans la direction de projection.
, le noyau d'une projection sur un plan est la droite dans la direction de projection.
![]()
![]() , projection
, projection ![]() sur une droite.
sur une droite.
![]() ,
,
![]()
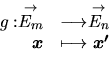
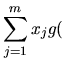
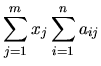
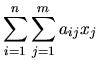
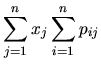
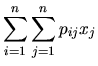
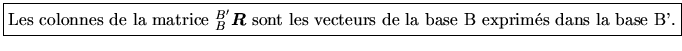
![]()
![]() est dite carrée si
est dite carrée si ![]() . Dans une matrice carrée, les éléments de (1,1) à (n,n) forment la diagonale principale.
. Dans une matrice carrée, les éléments de (1,1) à (n,n) forment la diagonale principale.
![]() , on la note
, on la note ![]() Pour toute matrice
Pour toute matrice
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() telle que pour tout vecteur
telle que pour tout vecteur ![]() non nul,
non nul,
![]()
![]()
![]()
![]()
![]() telle que pour tout vecteur
telle que pour tout vecteur ![]() non nul,
non nul,
![]()
![]()
![]()
![]()
![]()
![]() est la matrice associée à une application linéaire
est la matrice associée à une application linéaire ![]() et
et ![]() la matrice associée à une application linéaire
la matrice associée à une application linéaire ![]() , alors
, alors ![]() est la matrice associée à l'application linéaire
est la matrice associée à l'application linéaire ![]() .
.
![]() sont considérés comme des matrices à
sont considérés comme des matrices à ![]() lignes et une colonne.
lignes et une colonne.
![]()
![]() peut admettre une pseudo-inverse
peut admettre une pseudo-inverse
![]()
![]() telle que
telle que
![]()
![]()
![]() (plus de détails en section
(plus de détails en section ![]() )
)
![]() un élément de
un élément de ![]() .
Notons
.
Notons
![]() , la matrice de taille
, la matrice de taille
![]() obtenue en retirant la ligne
obtenue en retirant la ligne ![]() et la colonne
et la colonne ![]() de
de ![]() . Le déterminant de
. Le déterminant de
![]() est appelé cofacteur de
est appelé cofacteur de ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() la matrice des cofacteurs. L'inverse de
la matrice des cofacteurs. L'inverse de ![]() vaut:
vaut:
![]()
![]() (méthode de calcul extêmement inefficace)
(méthode de calcul extêmement inefficace)
![]() s'effectue en résolvant le système d'équations:
s'effectue en résolvant le système d'équations:
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0. On obtient une famille de solutions qui constitue le sous-espace propre associé à
0. On obtient une famille de solutions qui constitue le sous-espace propre associé à ![]() .
.
![]()
![]() ):
):
![]() . On peut en effet remplacer
. On peut en effet remplacer ![]() par
par
![]()
![]() pour tout
pour tout ![]() .
.
![]() est unitaire:
est unitaire:
![]() et l'angle
et l'angle ![]() d'après la matrice
d'après la matrice ![]() . Il n'y a pas de solution unique (angle défini à
. Il n'y a pas de solution unique (angle défini à ![]() près, axe ou son opposé). On peut en trouver une en remarquant que
près, axe ou son opposé). On peut en trouver une en remarquant que
![]()
![]()
![]() et que
et que
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (matrices définies en éq.
(matrices définies en éq. ![]() ) peut s'interpêter de deux manières mathématiquement équivalentes mais intuitivement différentes:
) peut s'interpêter de deux manières mathématiquement équivalentes mais intuitivement différentes:
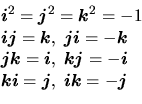
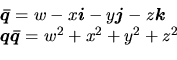
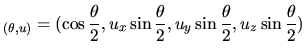
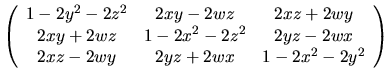

![]() quaternions en obtenir
quaternions en obtenir ![]() :
:
![]() la rotation subie par
la rotation subie par
![]() entre l'instant
entre l'instant ![]() et l'instant
et l'instant ![]() . Nous pouvons écrire:
. Nous pouvons écrire:
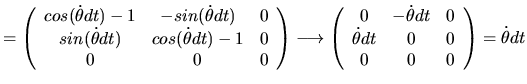
![]() :
:
![]()
![]()
![]()
![]()
![]() , ou en simplifiant la notation:
, ou en simplifiant la notation:
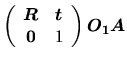
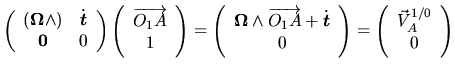
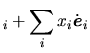
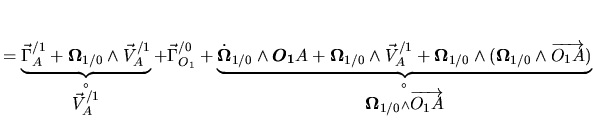
![]()
![]() traduit la position de la liaison par rapport à
traduit la position de la liaison par rapport à
![]() . La matrice
. La matrice
![]()
![]() traduit le deplacement dans la liaison, par rapport à une position de référence. Elle peut varier avec le temps et conformement aux ddl. La matrice
traduit le deplacement dans la liaison, par rapport à une position de référence. Elle peut varier avec le temps et conformement aux ddl. La matrice
![]()
![]() (plus précisement, son inverse) traduit la position de la liaison par rapport à
(plus précisement, son inverse) traduit la position de la liaison par rapport à
![]() .
.
![]() présente un exemple de chaîne articulée. Un socle mobile de repère
présente un exemple de chaîne articulée. Un socle mobile de repère
![]() peut se déplacer sur le sol de repère
peut se déplacer sur le sol de repère
![]() . Un bras de repère
. Un bras de repère
![]() est articulé par rapport au socle mobile. À doite de la figure, le graphe cinématique représente l'accrochage des solides (noeuds) par les liaisons (arcs). Ce graphe est orienté en partant du repère absolu, qui est toujours à la racine.
est articulé par rapport au socle mobile. À doite de la figure, le graphe cinématique représente l'accrochage des solides (noeuds) par les liaisons (arcs). Ce graphe est orienté en partant du repère absolu, qui est toujours à la racine.
![]() qui définit l'état du sytème. L'ensemble des états possibles est appelé espace articulaire du système. De même on peut regrouper les vitesses articulaires dans un vecteur
qui définit l'état du sytème. L'ensemble des états possibles est appelé espace articulaire du système. De même on peut regrouper les vitesses articulaires dans un vecteur
![]() .
.
![]() présente un algorithme de calcul des matrices de passage de chaque solide de la chaîne.
présente un algorithme de calcul des matrices de passage de chaque solide de la chaîne.
![]() présente un algorithme de calcul de vitesses. Les données sont:
présente un algorithme de calcul de vitesses. Les données sont:
![]() .
.
![]() doit se positionner sur la droite définie par un point
doit se positionner sur la droite définie par un point ![]() et un vecteur normal
et un vecteur normal
![]()
![]() , comme illustré sur la figure
, comme illustré sur la figure ![]() . Nous sommes en présence d'une contrainte scalaire, puisqu'on peut l'exprimer par une équation unique
. Nous sommes en présence d'une contrainte scalaire, puisqu'on peut l'exprimer par une équation unique
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
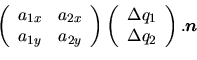
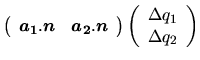
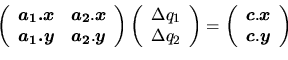
![]() influencée par des ddl numerotés de
influencée par des ddl numerotés de ![]() à
à ![]() .
Nous pouvons regrouper toutes les dérivées partielles en colonnes dans une matrice appelée matrice jacobienne de vitesse (ou de petit déplacement) au point
.
Nous pouvons regrouper toutes les dérivées partielles en colonnes dans une matrice appelée matrice jacobienne de vitesse (ou de petit déplacement) au point ![]() :
:
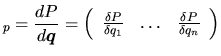
![]()
![]()
![]()
![]()
![]() se traduisent par une équation:
se traduisent par une équation:
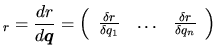
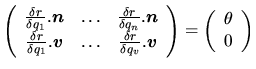
![]()
![]() , dans le cas contraire elle minimise
, dans le cas contraire elle minimise
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() applique cette idée.
applique cette idée.