| The Java 3D API Specification |
|
| The Java 3D API Specification |
|
A P P E N D I X  B B |
|
3D Geometry Compression |
B.1
The process of geometry compression is as follows:Compression 1. The geometry to be compressed is converted into a generalized mesh form, which allows a triangle to be, on average, specified by 0.80 vertices.
2. The data for each vertex component of the geometry is converted to the most efficient representation format for its type and then quantized to as few bits as possible.
3. These quantized bits are differenced between successive vertices, and the results are modified Huffman-encoded into self-describing variable-bit-length data elements.
4. These variable-length elements are strung together into a final compressed geometry block using compressed geometry's seven geometry instructions.
B.2
For pure software implementations, upon receipt, compressed geometry blocks are decompressed into the local host's preferred geometry format by reversing the compression process. This decompression can be performed in a lazy manner, avoiding full expansion into memory until the geometry is needed for rendering.Decompression
B.3
Before the bit details of the compression can be specified, several of the concepts used in compressed geometry need elaboration. The first several sections are an expansion of our SIGGRAPH '95 paper on compressed geometry.1Appendix Organization
- Generalized Triangle Strip. This section is a refresher on the concept and semantics of a generalized triangle strip.
- Generalized Triangle Mesh. This section introduces the concept and semantics of a generalized triangle mesh.
- Position Representation and Quantization. This section describes the fixed-point format used for 3D positional representation.
- Color Representation and Quantization. This section describes the fixed-point format used for color representation.
- Normal Representation and Quantization. This section describes a novel folded table-based representation of surface normals, and the fixed-point format of the resultant normals.
- Modified Huffman Encoding. This section describes the variant of Huffman delta encoding used for compressed geometry.
- Compressed Geometry Instructions. This section gives an overview of the seven compressed geometry instructions.
- Semantics of Compressed Geometry Instructions. This section contains pseudocode to document the detailed semantics of compressed geometry instruction execution.
- Compressed Geometry Assembly Syntax. This section gives an overview of the assembly syntax for compressed geometry instructions.
B.4
A generalized triangle strip is a generalization of the concept of a "zig-zag" and triangle fan. It is a sequence of vertices in which each vertex contains a two-bit replacement code. This replacement code defines how the present vertex is to be combined with previous vertices to form the next triangle. The replacement bits can also be thought of as a generalization of the "move/draw" bit used for lines.Generalized Triangle Strip
Restartcorresponds to a "move" operation in polylines and allows multiple, unconnected, variable-length triangle strips to be described by a single data structure passed in by the user, greatly reducing the overhead. The generalized triangle strip's ability to effectively change from "strip" to "fan" mode in the middle of a strip allows more complex geometry to be represented compactly and requires less input data bandwidth. The restart capability allows several pieces of disconnected geometry to be passed as one data block. Figure B-1 shows a single generalized triangle strip and the associated replacement codes.
Figure B-1
A Generalized Triangle Strip
B.5
The first stage of compressed geometry is to convert triangle data into an efficient linear strip form: the generalized triangle mesh. This is a near-optimal representation of triangle data, given fixed storage.Generalized Triangle Mesh However, by confining itself to linear strips, the generalized triangle strip format leaves a potential factor of two (in space) on the table. Consider the geometry in Figure B-2.
The fixed mesh buffer size requires all tessellators or restripifiers for compressed geometry to break up any runs longer than 16 unique references. Since compressed geometry is not meant to be programmed directly at the user level, but rather by sophisticated tessellators or reformatters, this is not too onerous a restriction. Sixteen old vertices allow up to 94 percent of the redundant geometry to avoid being respecified. Figure B-2 also contains an example of a general mesh buffer representation of the surface geometry.
Figure B-2
A Generalized Triangle Mesh
B.6
The 8-bit exponent of 32-bit IEEE floating-point numbers allows positions literally to span the known universe: from a scale of 100 billion light years down to the radius of subatomic particles. However, for any given tessellated object the exponent is really specified just once by the current modeling matrix; within a given modeling space, the object geometry is effectively described with only the 24-bit fixed-point mantissa. Visually, in many cases far fewer bits are needed; thus the language of compressed geometry supports variable quantization of position data down to as little as one bit. The maximum number of bits supported is at most 16 bits of precision per component of position.Position Representation and Quantization
B.7
We treat colors similar to positions, but without using negative values. Thus RGBColor Representation and Quantization color data is first quantized to 15-bit unsigned fraction components, and a zero sign bit is added to form a 16-bit signed number. These are absolute linear reflectivity values, with 1.0 representing 100 percent reflectivity. An additional parameter allows color data to be quantized effectively to any amount less than 16 bits; that is, the colors can all be within a 5-5-5 RGB color space. (The
field is optional, controlled by the color alpha present (
cap) state bit.) Note that this decision does not necessarily cause mach banding on the final rendered image; individual pixel colors are still interpolated between these quantized vertex colors, and vertices also are subject to lighting.
B.8
Probably the most innovative concept in compressed geometry is the method of compressing surface normals. Traditionally, 96-bit normals (three 32-bit IEEE floating-point numbers) are used in calculations to determine 8-bit color intensities. Theoretically, 96 bits of information could be used to represent 296 different normals, spread evenly over the surface of a unit sphere. This is a normal every 2-46 radians in any direction. Such angles are so exact that by spreading angles out evenly in every direction from earth, you could point out any rock on Mars with subcentimeter accuracy.Normal Representation and Quantization During the normal transformation, floating-point arithmetic hardware effectively truncates all additive arguments to the accuracy of the largest component. The result is that for a normalized normal being transformed by a scale-preserving modeling orientation matrix, the numerical accuracy of the transformed normal value is reduced to no more than 24-bit fixed-point accuracy in all but a few special cases.
- T0,02 + T1,02 + T2,02 = 1, etc.
B.8.1
The most obvious hardware implementation for converting an index of a normal on the unit sphere back into an Nx Ny Nz value is by table look-up. The problem is the size of the table. Fortunately, several symmetry tricks can be applied to reduce the size of the table greatly (by a factor of 48).Normals as Indices First, the unit sphere is symmetrical in the eight quadrants by sign bits. In other words, if we let three of the normal representation bits be the three sign bits of the XYZ components of the normal, then we need only to find a way to represent one eighth of the unit sphere. The all positive sign bit octant of the unit sphere is shown in bold outline on the left half of Figure B-3. This 000 sign bit octant will be referred to as the prime octant.
Second, each octant of the unit sphere can be split into six identical pieces by folding about the planes X = Y, X = Z, and Y = Z. Such a division of the prime octant is shown in Figure B-3. The six possible sextants are encoded with another three bits. Now only 1/48 of the sphere remains to be represented.
- We desire a scalable density distribution in which zeroing more and more of the low-order address bits to the table still results in fairly even density of normals on the unit sphere. Otherwise a different look-up table for every encoding density would be required.
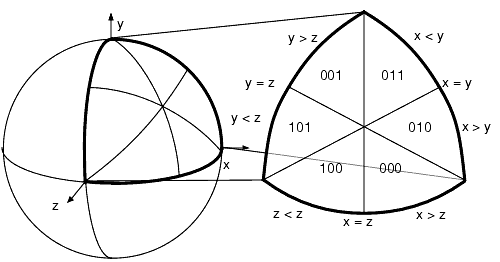
Figure B-3
Encoding of the Six Sextants of Each Octant of a Sphere
- We desire a delta-encodable distribution. Statistically, adjacent vertices in geometry will have normals that are nearby on the surface of the unit sphere. Nearby locations on the 2D space of the unit-sphere surface are most succinctly encoded by a 2D offset. We desire a distribution where such a metric exists.
For all these reasons, we decided to use a regular grid in the angular space within one sextant as our distribution. Thus, rather than a monolithic 11-bit index, all normals within a sextant are much more conveniently represented as two 6-bit orthogonal angular addresses, revising our grand total to 18 bits. Just as for positions and colors, if more quantization of normals is acceptable, then these 6-bit indices can be reduced to fewer bits; thus absolute normals can be represented using anywhere from 18 to as few as 6 bits. But as will be seen, we can delta-encode this space, further reducing the number of bits required for high-quality representation of normals.
- Finally, while the computational cost of the normal encoding process is not too important, in general, distributions with lower encoding costs are preferred.
B.8.2
Points on a unit radius sphere are parameterized by two angles,Normal Encoding Parameterization and
, using spherical coordinates.
is the angle about the Y-axis;
is the longitudinal angle from the y = 0 plane. The mapping between rectangular and spherical coordinates is as follows:
Note that many different incompatible definitions of spherical coordinates exist within mathematics and engineering. For the purposes of compressed geometry, spherical coordinates used are those defined by equation B.1.
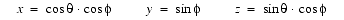
(Eq. B.1) This triangular-shaped patch runs from 0 to
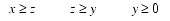
/4 radians in
, and from 0 to as much as 0.615479709 radians in
:
max.
Quantized angles are represented by two n-bit integers
and
, where n is in the range of 0 to 6. The sextant coordinate system defined by these parameters is shown in Figure B-4, for the case of n = 6. For a given n, the relationship between these indices
and
is
These two equations show how values of
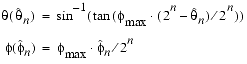
(Eq. B.2) and
can be converted to spherical coordinates
and
, which in turn can be converted to rectilinear normal coordinate components via equation B.1.
To reverse the process, for example, to encode a given normal n into
and
, one cannot just invert equation B.2. Instead, the n must first be folded into the canonical octant and sextant, resulting in n'. Then n' must be dotted with all quantized normals in the sextant. For a fixed n, the values of
and
that result in the largest (nearest unity) dot product define the proper encoding of n.
Now the complete bit format of absolute normals can be given. The uppermost three bits specify the sextant, the next three bits specify the octant, and finally two n-bit fields specify
and
. The three-bit sextant field takes on one of six values, the binary codes for which are shown in Figure B-3.
Figure B-4
Sextant Coordinates
B.8.3
With some additional work, this can be extended to sextants that share a common edge. First we must define how sextants border each other. Consider the three edges of the sextant coordinate system as defined in Figure B-4, and also examine Figure B-3 to see the sextant connectivity within an octant and between octants. The three possible neighbors of a sextant are shown schematically in Figure B-5.Special Warping Rules for Delta Normals
Figure B-5
Sextant Neighbors and Their Relationships
For a given value of n (in the range of 1 to 6), where n is the number of bits of quantization of the sextant coordinates, the valid coordinates are bounded by
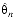
0,
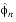
0, and
+
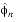
2n. For any given sextant number, the left and diagonal neighbors of that sextant are explicitly known. The bottom edge of a sextant will be the same sextant number, but in a different octant. The octant will differ from the current octant by the flip of exactly one of the sign bits. Which octant sign bit will be flipped is also explicitly known. The rules for finding each edge neighbor for any sextant are given in Table B-1.
The special rules for wrapping during normal deltas follow:
- Normal Case:
- if
+
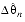
0 ,
+
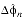
0,
+
+
+
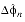
2n :
- Left Edge Wrap Case:
- if
+
< 0 ,
+
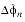
0, -(
+
) +
+
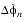
2n :
- current sextant is updated from left edge rules in Table B-1 and current octant is unchanged.
- Diagonal Edge Wrap Case:
- if
+
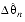
0 ,
+
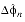
0,
+
+
+
> 2n :
- new
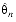
2n - (
+
) , new
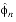
2n - (
+
) ,
- current sextant is updated from diagonal edge rules in Table B-1 and current octant is unchanged.
- Bottom Edge Wrap Case:
Any wrap that does not fall into one of these categories is an illegal delta and is not allowed within a valid compressed geometry stream.
- if
+
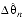
0 ,
+
< 0,
+
- (
+
)
2n :
- current sextant is unchanged, and current octant is updated from bottom edge rules in Table B-1.
B.9
There are many techniques known for minimally representing variable-length bit fields. For compressed geometry, we have chosen a variation of the conventional Huffman technique.Modified Huffman Encoding The binary format for compressed geometry uses this technique to represent position, normal, and color data fields. For compressed geometry, these <tag, data> fields are immediately preceded by (a more conventional computer instruction set) opcode field. These fields, plus potential additional operand bits, are referred to as geometry instructions (see Figure B-6).
Figure B-6
Bit Layout of Compressed Geometry Instructions
This header forwarding is applied to all instructions. The vertex instruction optionally had one or two subfields that need forwarded headers. In these special cases the headers are only six bits in length, because no opcode is present.
H1 B0 H2 B1 H3 B2

B.10
Java 3D's compressed geometry protocol defines seven instructions to be used in specifying 3D geometry and certain affiliated attributes. Table B-2 gives a brief overview of these instructions and some of their semantics. More detail of these instructions, including their bit layout, is given in the following sections.Compressed Geometry Instructions
B.11
Figure B-6 shows the bit-level layout of the seven geometry decompression instructions. Each instruction has a unique opcode and then some (usually fixed number of) arguments. In the case of theBit Layout of Compressed Geometry Instructions setColorinstruction, the number of arguments can be either three or four, depending on the current setting of thecapbit (set by thesetStateinstruction). In the case of the vertex instruction, the number of arguments also varies by the current setting of thesetStateinstruction.
B.12
The following subsections describe the bit details of the compressed geometry instructions as well as much of their associated semantics. Along with each instruction, its assembly (and disassembly) syntax is described.Compressed Geometry Instruction Bit Details Assembly syntax:
(nop <Bit count>)Assembly syntax:
(setState {normalsBundled}
{colorsBundled} {alphaBundled})Assembly syntax:
(setTable <Table> <start fill>-<end fill>
<Data Length> <Up-shift> <A/R>)The 2-bit table specifies for which of the three decompression tables this update is targeted:
00 Position 01 Color 10 Normal 11 Unused-reserved for future use
B.12.4
mbr (meshBufferReference) Instruction 
Assembly syntax:
(mbr <rep> <index>)
RST Restart RSTR Restart reverse RMID Replace middle ROLD Replace oldest
0 0 Restart reverse 0 1 Restart 1 0 Replace middle 1 1 Replace oldest
B.12.5
Position Subinstruction 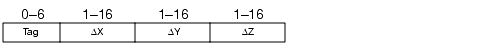
Assembly syntax:
(Position <Tag> <X> <Y> <Z>)Assembly syntax:
(Color <Tag> <R> <G> <B> {<>})Assembly syntax: absolute:
(Normal <Tag><Sextant><Octant><><>)Assembly syntax: relative:
(Normal <Tag> <> <>)Assembly syntax: special:
(Normal <Tag> <Special>)Assembly syntax: <Sextant>:
0,1,2,3,4,5(as specified in Figure B-3)Assembly syntax: Table B-3 shows the assembly format for specifying octants in the <octant> field of
Normalsubinstructions (as well assetNormalinstructions).
Table B-3 Syntax for Specifying Octants
Syntax Octant +++ +X +Y +Z ++- +X +Y -Z +-+ +X -Y +Z +-- +X -Y -Z -++ -X +Y +Z -+- -X +Y -Z --+ -X -Y +Z --- -X -Y -Z
Assembly syntax: Table B-4 shows the assembly syntax for specifying the special normals in the "Special" field of
Normalsubinstructions (as well assetNormalinstructions).
A number of normals lie on the edges or corners where sextants meet (e.g., at
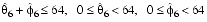
= 0 and
= 0). These normals do not have a unique encoding; the same normal can be specified using different sextants or octants. All of these encodings are legal; usually the choice of encoding is decided by using the one that makes it the easiest to compute deltas from the previous and/or to the following normal.
Fourteen special absolute normals are encoded by the unused two settings within the three sextant bits. This is indicated by specifying the angle fields to have a length of zero (not present) and the first two bits of the sextant field to both have a value of 1. Table B-5 lists the 14 special normals
RST Restart RSTR Restart reverse RMID Replace middle ROLD Replace oldest
0 0 Restart reverse 0 1 Restart 1 0 Replace middle 1 1 Replace oldest
Assembly syntax: absolute:
(setNormal <Tag> <Sextant> <Octant>
<> <>)Assembly syntax: relative:
(setNormal <Tag> <> <>)Assembly syntax: absolute special:
(setNormal <Tag> <Special>)Assembly syntax:
<Sextant>, <Octant>, <Special>: same as for normal subinstruction.The
setNormalinstruction has a two-bit opcode and aNormalsubinstruction.The
Normalsubinstruction has the semantics documented in Section B.12.7, "Normal Subinstruction."Assembly syntax:
(setColor <Tag> <R> <G> <B> {<>})The
setColorinstruction has a two-bit opcode, and acolorsubinstruction. Thecolorsubinstruction semantics are documented in Section B.12.6, "Color Subinstruction."
B.13
The formal semantics of the compressed geometry format is best described by a state description of the decompression process. It must be emphasized that these state descriptions are given to show the formal semantics, not an efficient implementation.Semantics of Compressed Geometry Instructions
B.13.1
Compressed geometry instructions have a minimum length of eight bits (six bits for subinstructions). This allows all geometry decompression instructions to be split into two physically separate bit sequences within the compressed stream. The first bit sequence is always of eight bits in length (six for subinstructions); the second bit sequence contains the remaining bits of the instruction (if any). Thus a logical stream of N compressed geometry instructions, where each instruction is split into two bit sequences Hi and Bi (i being from 0 to N - 1), is physically represented asHeader and Body to Variable-Length Instruction Okay, so what is this "B-1"? All compressed geometry sequences have an implied (not physically present) H-1 of a nop opcode, thus B-1 is always present (starting at the eighth bit of the stream) as any valid variable-length nop body. (Just five zeros, the minimum-length nop, is a good default.) Thus the implied nop opcode "jump starts" the header-forwarded decompression process. This process is reversed at the end of the stream. Hn is a nop opcode, but no body is present, as Bn-1 is the last bits of the stream. (As will be described, Bn-1 must end on a 32-bit aligned boundary.)
- H0 B-1 H1 B0 H2 B1 ... Hn-1 Bn-2 Hn Bn-1
One slight complexity: The
// pseudocode for converting bitstream into sequences of // instructions decompress(stream) { current_header <- nop while (not_empty(stream)) { next_header <- get_header_bits(stream) current_body <- get_n_bits(stream, body_length(previous_header)) process_instruction(current_header, current_body) current_header <- next_header } }get_header_bits()extracts only six bits of header forcolorornormalsubinstructions of avertexinstruction. It extracts a full eight bits of header in all other cases.
B.13.2
The three decompression tables contain entries for each different numeric tag describing whether the value in the stream is absolute or relative, and length and shift constants describing how to convert the variable-length bit field back into a fixed-length value. The fixed-length value for position and color components is 16 bits in length (sign, unit, 14 fraction); the fields for normal angles are 7 bits (signed) and 3 each for sextant and octant (if present).Variable-Length Instruction to Instruction
B.13.3
Delta Position to Position absolute_position(x, y, z):cur_xx, cur_y
y, cur_z
z
relative_position(x,
y,
z):
cur_xcur_x +
x, cur_y
cur_y +
y, cur_z
cur_z +
z
B.13.4
Delta Color to Color absolute_color(r, g, b {,}):
cur_rr, cur_g
g, cur_b
b, {cur_
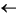
}
relative_color(r,
g,
b {,
}):
cur_rcur_r +
r, cur_g
cur_g +
g, cur_b
cur_b +
b, {cur_
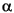
cur_
+
}
B.13.5
State:Encoded Delta Normal to Encoded Normal cur_oct,cur_sex,cur_u,cur_vabsolute_normal(oct, sex, u, v):cur_octoct, cur_sex
sex, cur_u
u, cur_v
v
relative_normal(u,
v):
cur_ucur_u +
u, cur_v
cur_v +
v, if (cur_u < 0) cur_u
-cur_u, cur_sex
flip_u[cur_sex] else if (cur_v < 0) cur_v
-cur_v, cur_oct
cur_oct <xor> flip_v[cur_sex] else if (cur_u + cur_v > 64) cur_u
64 - cur_u, cur_v
64 - cur_v, cur_sex
flip_uv[cur_sex] flip_u[6] = { 4, 5, 3, 2, 0, 1 } flip_v[6] = { 2, 4, 1, 1, 2, 4 } flip_uv[6] = { 2, 3, 0, 1, 5, 4 }
B.13.6
Encoded Normal to Rectilinear Normal
nxnorms[v,u].nx, ny
norms[v,u].ny, nz
norms[v,u].nz,
if (cur_sex & 4) tThe contents of thenx, nx
nz, nz
t if (cur_sex & 2) t
ny, ny
nz, nz
t if (cur_sex & 1) t
nx, nx
ny, ny
t if (cur_oct & 1) nz
-nz if (cur_oct & 2) ny
-ny if (cur_oct & 4) nx
-nx
norms[]table is exactly specified, and the next revision of this specification will contain an exact listing of the values.
B.14
The formal semantics of the vertex processing is best described by a state description of the decompression process. Once again it must be emphasized that these state descriptions are given to show the formal semantics, not an efficient implementation.Semantics of Vertices
B.14.1
This section describes the state change semantics caused by each instruction to generate the next output vertex, prior to assembly into triangles. The internal state consists of the three bundling bits, a current normal and current color,Instruction to Vertex normal_overrideandcolor_overridebits, the 16 mesh buffer vertices, and a current internal-cycling mesh buffer index.normal(n):current_normaln, normal_override
1
color(c):current_colorc, color_override
1
vertex(rep, mbp, p {, n} {, c}):
current_positionp, if (bnv) current_normal
n, if (bcv) current_color
c, output_vertex(rep, current_position, current_normal,
current_color) if (push) mesh_buffer[mesh_index].positionp if (push && bnv) mesh_buffer[mesh_index].normal
n if (push && bcv) mesh_buffer[mesh_index].color
c if (push) mesh_index
(mesh_index+1) & 15 normal_override
0, color_override
0
mesh buffer reference(rep, i):
current_positionmesh_buffer[(mesh_index - i - 1) & 15].position if (bnv && !normal_override) current_color
mesh_buffer[(mesh_index - i - 1) & 15].color if (bcv && !color_override) current_color
mesh_buffer[(mesh_index - i - 1) & 15].color normal_override
0, color_override
0 output_vertex(rep, current_position, current_normal, current_color)
set state(new_bnv, new_bcv, new_cap):
bnvnew_bnv, bcv
new_bcv, cap
new_cap, normal_override
0, color_override
0
set table(address, range, entry):...nop(length):(null)B.14.2
This section describes the formal semantics of assembling vertices with replacement instructions into nearly finished triangles: the semantics of generalized triangle strips.Vertex to Intermediate Triangle output_vertex(restart_reverse, newv):newestnewv, number_of_vertices
1, rev = 1
output_vertex(restart, newv):newestnewv, number_of_vertices
1, rev = 0
output_vertex(replace_middle, newv):
if (number_of_vertices < 2) middlenewest, newest
newv, number_of_vertices++ else if (number_of_vertices < 3) oldest
middle, middle
newest, newest
newv, number_of_vertices++, intermediate_triangle(restart, oldest, middle, newest) else if (number_of_vertices == 3) middle
newest, newest
newv, intermediate_triangle(restart, oldest, middle, newest)
output_vertex(replace_oldest, newv):
if (number_of_vertices < 2) middlenewest, newest
newv, number_of_vertices++ else if (number_of_vertices < 3) oldest
middle, middle
newest, newest
newv, number_of_vertices++, intermediate_triangle(restart, oldest, middle, newest) else if (number_of_vertices == 3) oldest
middle, middle
newest, newest
newv, rev = 1 - rev, intermediate_triangle(restart, oldest, middle, newest)
B.14.3
The final stage is to take into account the current reverse bit. This bit controls the order in which the vertices are output to ensure they all face the correct way.Intermediate Triangle to Final Triangle intermediate_triangle(rev, v1, v2, v3):
if (!rev) final_triangle(v1.position, v1.normal, v1.color, v2.position, v2.normal, v2.color, v3.position, v3.normal, v3.color) else if (rev) final_triangle(v2.position, v2.normal, v2.color, v1.position, v1.normal, v1.color, v3.position, v3.normal, v3.color)B.15
Java 3D formally defines only the compressed geometry format and the decompression semantics. Authoring tools are free to employ whatever compressed geometry algorithms they choose, as long as the results adhere to the specifications described in the previous sections.Outline of Geometry Process
B.15.1
Group the geometry to be compressed into separate rigid objects. Typically such objects will be individually culled during rendering, so you should not join objects too extensively prior to compression. In optimized systems, the granularity of object splitting will be computed by an algorithm that takes culling optimization into account (both frustum and occlusion culling).Compressing Geometry Data
B.15.2
Once a group of geometry has been identified, it is next converted into generalized mesh format. This is a complex step, and a number of topological analysis-based algorithms have been applied to it. Note that to reduce compression time, when space is a less important issue than time, a compressor might only stripify, not meshify. Alternatively, the triangles have to have come from somewhere, and that in many cases is a tessellator of higher order surfaces. Such a tessellator will implicitly know the mesh connectivity and may be able to generate the triangle data directly in the generalized mesh format.Convert to Generalized Mesh Format
B.15.3
Position Normalize the position data.
The containing bounding box for the object is computed. This is the minimal box such that all geometry vertices are contained within it. The vertices are then all normalized to be contained within this bounding box by first subtracting the XYZ location of the bounding box center from the vertex XYZ and then dividing all the XYZ vertex values by the half length of the longest side of the bounding box. Thus all normalized positions will be within the ±1 unit cube. A constant matrix transform corresponding to an offset to the center of the bounding box and an inverse scale by the half length of the longest side of the bounding box are created as a prologue for the geometry data. Note that in practice a little more care must be taken. The greatest positive value is actually, when positions are quantized to n bits. By symmetry, the smallest negative value allowed is
. The value -1 (only sign bit set, all other bits 0) is explicitly not allowed. Thus when computing the scale factor (and center) that will normalize the geometry, the actual representation range needs to be taken into account.
Quantize the position data.
Assuming that position data is to be quantized to n bits, each vertex position component should be multiplied by the value of 2n and then rounded down to the nearest integer. If rounded to the nearest integer, or rounded up, the value may overflow the representation. Once again the goal is to take numbers from a given floating point range and represent all of them within an n-bit fixed point range.
B.15.4
Normals Normalize the normals.
Each normal should be normalized to unit length.
Quantize the XYZ components of the normal to 14 bits accuracy.
Each normal component should be multiplied by 214, rounded to the nearest integer, and then converted back to floating-point representation and divided by 214.
Fold the XYZ components of the normal to the positive (prime) octant.
If an XYZ component of the normal is negative, invert it and save the original sign bits as a three-bit octant value. It is important when compressing always to strip the sign bits off first before applying sextant folding and to reverse the process when decompressing. Note that the octant bits read left to right: the upper bit is for the x-axis, the middle for the y-axis, and the lowermost is for the z-axis.
oct = 0; if(nx < 0.0) oct |= 4, nx = -nx if(ny < 0.0) oct |= 2, ny = -ny if(nz < 0.0) oct |= 1, nz = -nzFold the normal to the nX
Check (in exactly the following order):nZ
nY sextant.
sex = 0; if (nx < ny) t = nx, nx = ny, ny = t, sex |= 1 if (nz < ny) t = ny, ny = nz, nz = t, sex |= 2 if (nx < nz) t = nx, nx = nz, nz = t, sex |= 4Match the nearest quantized normal representation.
Take the dot product of the normal with each of the quantized reference normals in the table for the specified number of quantized normal bits. That u,v normal index for the reference normal that gives the greatest (nearest unity) dot product result is the new quantized normal representation (along with the octant and sextant representation). (There are more efficient ways to compute the same results.) At this point there are no specific tie-breaking rules when two (or more) reference normals produce the same candidate dot product results. Technically this is purely a compressor internal issue.
Check for special normals.
The u,v normal index generated by the previous stage will generally be in the full 7-bit range of the normal grid space. In this space, the two classes of special normals occur when u = 64, v = 0, and when u = 0, v = 64. When this is detected, the sextant and octant bits must be examined to produce the proper special normal encoding:
if (u == 64 && v == 0) { /* Six coordinate axis case */ if (sex == 0 || sex == 2) /* +/- x-axis */ special = ((oct & 4)?0x2:0); else if (sex == 3 || sex == 1) /* +/- y-axis */ special = 4 | ((oct & 2)?0x2:0); else if (sex == 5 || sex == 4) /* +/- z-axis */ special = 0x8 | ((oct & 1)?0x2:0); } else if (u == 0 && v == 64) /* Eight mid point case */ special = (oct<<1) | 1;B.15.5
To begin with, the colors are assumed to be in a 0.0 to 0.9 representation.Colors
Quantize the color values.
Assuming that color data is to be quantized to n bits, each vertex color component (R, G, B, and optionally) should be multiplied by the value of 2n and then rounded down to the nearest integer. Just as with positions, there is no true representation of positive unity.
B.15.6
Make a pass in generalized mesh order through all vertices in the geometry. For each successive pair of vertices, compute the difference between their component values, compute the bit length of this (signed) difference, and histogram this bit length. Specifics for each component type are detailed in the following sections.Collect Delta Code Statistics
B.15.7
ComputePosition Delta Code Statistics X,
Y, and
Z. Determine which of these has the greatest magnitude. Compute the number of bits for this component, including one sign bit. This is the length to be histogrammed for positions.
B.15.8
ComputeColor Delta Code Statistics R,
G,
B, and
(if present). Determine which of these has the greatest magnitude. Compute the number of bits for this component, including one sign bit. This is the length to be histogrammed for colors.
B.15.9
For a given pair of normals, check to see if they have the same octant and sextant, and that neither is a special normal. If so, computeNormal Delta Code Statistics U and
V. Determine which of these has the greatest magnitude. Compute the number of bits for this component, including one sign bit. This is the length to be histogrammed for this pair of normals.
If the normals have different sextants and/or octants, but neither is a special normal, check to see if their sextants share an edge. If so, the special normal wrapping rules from Section B.8.3, "Special Warping Rules for Delta Normals," can be applied. Depending on what type of edge they share, the delta including the change in edges is encoded in one of three ways: U +
U < 0, V +
V < 0, and U +
U + V +
V > 64. Each case is discussed in the following paragraphs. The sextant numbers are from the binary codes shown in Figure B-3.
Note: When using the normal wrapping rules, a subtle bug can be introduced due to the ambiguity of normals on a shared edge between two sextants. The normal encoding rules have unambiguous tie-breaking rules to determine which octant and sextant a given normal resides in. However, the wrapping rules assume by default that a delta'd normal is in the same sextant and octant as its predecessor if the delta landed only on an edge. This is subtly different than the sextant and octant that the encoding rules might have suggested. The proper procedure is to keep track of which octant and sextant a decompressor would believe that the normals being generated would lie in. When the normal to delta to lands on an edge of this region, change its sextant and octant from what the encoding rules suggest are the same as where it is now delta-ing from. This change in default encoding is permissible because the rectilinear normal encoded by values on a sextant edge is identical no, matter which sextant claims ownership.
Otherwise the normals cannot be delta encoded, and so the second (target) normal must be represented by an absolute reference to its three octant, three sextant, and 2 n-bit u, v addresses. This is the length to be histogrammed for this pair of normals.
Note: Slightly higher compression density can be achieved at a slight expense in representation accuracy by avoiding special normals when delta and wrapping differences are generating compact results. Instead of generating the special normal, a near-by nonspecial normal can be generated allowing for compact deltas. As with any compression technique that intentionally further modifies or distorts the input data, doing this normal perturbation must be a policy choice of the compressor itself and subject to quality constraints of the user.
B.15.10
Encode data into variable-bit length compressed geometry instructions.Assign Huffman Tags
B.15.11
Given the sequence of variable-bit-length compressed geometry instructions, shuffle the first eight (six) bits of each instruction ahead of its predecessor's body.Assemble the Pieces into a Bit Stream
B.16
This section describes the assembly syntax for both the input to an assembler for compressed geometry, and for the output of a disassembler of compressed geometry.Compressed Geometry Assembly Syntax 1. Nearly raw. After a symbolic opcode, decimal (or optionally, hex) numbers are printed for the modified Huffman tag field and for all data fields without any additional interpretation, scaling, or un-delta-ing, except that proper signed/unsigned semantics are followed. The only processing is to parse the incoming bit stream into bit fields and to undo the effects of header forwarding. The modified Huffman tag is used only to determine the length of the tag field and the following data fields. The opcode has no trailing letter modifiers (as documented below); this indicates level 1.
Once again while the dissembler supports all 10 levels of output options, the assembler supports only levels 1 and 2.2. Same as level 1, but printed using hex numbers (preceded with a
0xsuffix).3. Modified Huffman tag expanded. The properties of the modified Huffman tag are shown in line: the length of the tag, the length of the data fields, and the left normalization shift for the field. The absolute/relative bit value is shown by appending the letter `A' or `R' to the opcode (or `S' for absolute `special' normals).
4. Same as level 3, but printed using hex numbers (preceded with the
0xsuffix).5. Normalized. The left normalization shift is applied to the data fields, and the specific properties of the modified Huffman tag are no longer shown. To differentiate from level 2, the letter `N' is appended to the opcode name after the absolute/relative/special letter.
6. Same as level 5, but printed using hex numbers (preceded with the
0xsuffix).7. Un-delta'd. Like level 3, but relative values have had the running total added to them to show what the current full value is. Absolute values are unchanged from level 3. To differentiate from level 4, an `A' suffix is added to the lengthening opcode name.
8. Same as level 7, but printed using hex numbers (preceded with the
0xsuffix).9. Floating point. While up to now all values have been subsets of 16-bit integers, before conversion to integer and quantization, most values were floating-point numbers in the 0 to 1.0 or -1.0 to 1.0 range. Level 5 shows the values as floating-point numbers, but it must be cautioned that these data fields, while similar to the input uncompressed unquantized values, will usually be slightly different in value than the original data. This floating-point output format is primarily included as a convenience when a user wants to understand the data closer to the original space.
10. Same as level 9, but non-floating-point numbers are printed using hex numbers (preceded with the
0xsuffix).
As an example, following is the disassembly (print level 1) of a four-sided pyramid:
(nop 0) (setTable Position 32-47 2 4 Rel) (setTable Position 56-63 3 4 Rel) (setTable Position 0-31 12 4 Rel) (setTable Position 48-55 12 4 Abs) (setTable Normal 0-31 5 0 Rel) (setTable Normal 32-63 6 0 Abs) (setTable Color 32-63 2 8 Rel) (setTable Color 0-31 8 8 Abs) (setState normalsBundled colorsUnbundled alphaUnbundled) (setState normalsBundled colorsUnbundled alphaUnbundled) (setColor 0 127 51 12) (setState normalsBundled colorsUnbundled alphaUnbundled) (setColor 32 0 0 0) (vertex RST (Position 48 -2047 -2047 -205) (Normal 32 4 --+ 44 0)) (vertex RMID (Position 0 2047 -2 0) (Normal 32 5 +++ 44 0)) (vertex ROLD (Position 0 0 -2047 409) (Normal 0 14 0)) (vertex ROLD (Position 0 2047 -2047 -409) (Normal 32 4 +-+ 44 0)) (vertex ROLD (Position 56 2 0 0) (Normal 32 4 --+ 44 0)) (vertex RST (Position 0 2047 -2 0) (Normal 32 00-)) (vertex RMID (Position 0 -2047 2 0) (Normal 32 00-)) (vertex ROLD (Position 32 -2 0 0) (Normal 32 00-)) (nop 19) (nop 29)B.17
This section describes the rules for determining if a given binary sequence is a valid compressed geometry block. These rules have been programmatically implemented in a compressed geometry verifier, a stand-alone C program that can validate a given file containing a Compressed Geometry object. The verifier is also available in a utility package in both C and Java for use within larger systems.Compressed Geometry Instruction Verifier
Rule 1: Size, Alignment and Byte Order
- Every compressed geometry is a sequence of binary data a multiple of four 8-bit bytes in size, starting on an aligned 32-bit boundary, represented in network byte order.
Rule 2: Beginnings
- Every compressed geometry sequence starts with the body field of a nop instruction. Initial process proceeds as if a forwarded header of a nop instruction had just been seen. The length field of this nop instruction body can be of any legal length, though usually by convention the length field is 0; thus the first body consists of five zeros.
Rule 3: Endings
- The last header in a compressed geometry sequence is a nop. This is followed by the body of the next-to-last instruction. This preceding instruction can be any instruction, and its body can be of any valid length for that instruction type, but the body must end on a four byte 32-bit word aligned boundary. To achieve this, usually the next-to-last and possibly the next-to-next-to-last instruction(s) are also nops, with lengths chosen to satisfy the ending requirement. Note that the body for the last instruction (the nop) is not present in the compressed geometry sequence. The end of the compressed geometry is determined from a separately specified size outside of the compressed geometry proper. Note that this ending convention is symmetrical with the starting convention; the sequential concatenation of two valid Compressed Geometry objects is also a valid Compressed Geometry object. For hardware, after a valid Compressed Geometry object has been executed, another valid compressed geometry can be executed without any pipeline flushes if desired.
Rule 4: Reserved Bits
- Any bits or bit fields described as reserved in a compressed geometry instruction must be filled with zeros.
Rule 5: Valid Opcodes
- Only the seven defined instruction opcodes may be present in a valid Compressed Geometry object.
Rule 6: No Defaults
- All state used in the processing of compressed geometry must be defined before it is used; there are no implicit defaults for any of the state. The state includes the contents of the decompression tables as defined by the setTable instruction; the three bundling bits as defined by the setState instruction; the contents of the mesh buffer as defined by vertex instructions with push enabled; and the current position, normal, and color (and alpha), as defined by absolute settings in vertex instructions, setNormal instructions, and setColor instructions. Note that this does not mean that all possible state needs to be defined within a Compressed Geometry object. For example, only those portions of the decompression tables actually referenced by a vertex or setNormal or setColor instruction need be initialized first. The bits specified by setState always need to be referenced, unless there are no vertex instructions, which would occur only in a geometry-less Compressed Geometry object. Mesh buffer elements need only be defined if they are accessed by mesh buffer reference instructions. The current normal and the current color (and alpha) are special cases; if they are not used within a Compressed Geometry object, they may not need to be initialized, depending on the semantics of the outer incorporating graphics API.
Rule 7: State Changes Immediately
- State changed by setState and setTable instructions is in force and available as of next instruction. (This specifically disallows pipelined hardware implementations from changing the semantics to force user-visible delay slots.)
Rule 8: Valid XYZ Positions
- Executing the position field of a vertex instruction will always result in a signed 16-bit fixed-point value for the current x, y, and z position state. All possible bit values are valid for these fields.
Rule 9: Valid Sextant Octant u v Normals
- Executing a setNormal instruction, or executing (when present) the normal subinstruction of a vertex instruction, will result in updated sextant, octant, u and v fields. The wrapping semantics described earlier define the subset of valid values and delta operations allowed for these fields. If these fields are valid, then a valid conversion back to a rectilinear Nx, Ny, Nz value is defined.
Rule 10: Valid RGB{
} Color
- Executing a setColor instruction, or executing (when present) the color subinstruction of a vertex instruction, will always result in a signed 16-bit fixed point value for the current R, G, B (and sometimes
) color state. Only positive values are valid for these fields.
Rule 11: What Is Outside the Scope of These Rules
As described earlier, for a Compressed Geometry object to be valid, it must follow these rules plus adhere to the other constraints on individual compressed geometry instructions described in the rest of this document.
- The results of executing a sequence of compressed geometry instructions in a valid Compressed Geometry object is a sequence of specific vertex values and connectivity information for triangles (or lines or points). What further processing this output stream is subject to, and the semantics of this processing is outside the scope of the specification of compressed geometry. For example, the semantics of transformation, lighting, and shading are not specified by compressed geometry. Note that even the semantic interpretation of what type of color parameter the "color" values generated by compressed geometry is left undefined by the Compressed Geometry specification; this is up to the lighting equation (or for realistic rendering systems, more generally the programmable shader) of the outer incorporating graphics API. Specifically no implication is made as to whether the "color" value is an ambient color, a diffuse color, a specular color, an emissive color, some combination thereof, or a more generalized value used by a programmable shader. This, of course, also applies to any interpretation of the
value, which may or may not be an opacity value.
| The Java 3D API Specification |
|