Math Objects

The Java 3D API Specification

MATHEMATICAL objects allow Java 3D users to represent and manipulate low-level mathematical constructs such as vectors and matrices. Math objects also define specific operations that allow users to manipulate them in appropriate ways.
Java 3D needs these vector and matrix math classes. It uses them internally and also makes them available to applications for their use. However, they are not part of Java 3D. Rather, they are defined here for convenience. These classes will become more widely distributed, which is why Java 3D defines them as a separate javax.vecmath package. Figure A-1 shows the math object hierarchy.

A.1 Tuple Objects
Java 3D uses tuple objects to represent and manipulate two-, three-, and four-element values.

A.1.1 Tuple2d Class
The Tuple2d class is used for points and vectors. This class is a two-element tuple that is represented by double-precision floating-point x,y coordinates.

Variables
The component values of a Tuple2d are directly accessible through the public variables x and y. To access the x component of a Tuple2d called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y component similarly.

Figure A-1 Math Object Hierarchy
public double x
Public double y
The x and y coordinates, respectively.

Constructors
public Tuple2d(double x, double y)
public Tuple2d(double[] t)
public Tuple2d(Tuple2d t1)
public Tuple2d(Tuple2f t1)
public Tuple2d()
Each of these five constructors returns a new Tuple2d. The first constructor generates a Tuple2d from two double-precision floating-point numbers x and y. The second constructor generates a Tuple2d from the first two elements of array t. The third and fourth constructors generate a Tuple2d from the tuple t1. The final constructor generates a Tuple2d with the value of (0.0, 0.0).

Methods
public final void set(double x, double y)
public final void set(double[] t)
public final void set(Tuple2d t1)
public final void set(Tuple2f t1)
public final void get(double[] t)
The first set method sets the value of this tuple to the specified xy coordinates. The second set method sets the value of this tuple from the two values specified in the array t. The third and fourth set methods set the value of this tuple to the value of the tuple t1. The get method copies the value of the elements of this tuple into the array t.
public final void add(Tuple2d t1, Tuple2d t2)
public final void add(Tuple2d t1)
public final void sub(Tuple2d t1, Tuple2d t2)
public final void sub(Tuple2d t1)
The first add method sets the value of this tuple to the vector sum of tuples v1 and v2. The second add method sets the value of this tuple to the vector sum of itself and tuple t1. The first sub method sets the value of this tuple to the vector difference of tuple t1 and t2 (this = t1 - t2). The second sub method sets the value of this tuple to the vector difference of itself and tuple t1 (this = this - t1).
public final void negate(Tuple2d t1)
public final void negate()
The first negate method sets the value of this tuple to the negation of tuple t1. The second method negates the value of this vector in place.
public final void scale(double s, Tuple2d t1)
public final void scale(double s)
public final void scaleAdd(double s, Tuple2d t1)
public final void scaleAdd(double s, Tuple2d t1, Tuple2d t2)
The first scale method multiplies each element of the tuple t1 by the scale factor s and places the resulting scaled tuple into this. The second method multiplies each element of this tuple by the scale factor s and places the resulting scaled tuple into this. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into the tuple this (this = s*this + t1). The second scaleAdd method scales tuple t1 by the scale factor s, adds the result to tuple t1, then places the result into the tuple this (this = s*t1 + t2).
public final void absolute(Tuple2d t)
This method sets each component of the tuple parameter to its absolute value and places the modified values into this tuple.
public final void clamp(double min, double max)
public final void clamp(double min, double max, Tuple2d t)
public final void clampMin(double min)
public final void clampMin(double min, Tuple2d t)
public final void clampMax(double max)
public final void clampMax(double max, Tuple2d t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps the values from tuple t to the range [min, max] and assigns these clamped values to this tuple. The first clampMin method clamps each value of this tuple to the min parameter. The second clampMin method clamps each value of the tuple t and assigns these clamped values to this tuple. The first clampMax method clamps each value of this tuple to the max parameter. The second clampMax method clamps each value of tuple t to the max parameter and assigns these clamped values to this tuple. In each method the values of tuple t remain unchanged.
public final void interpolate(Tuple2d t1, Tuple2d t2, double alpha)
public final void interpolate(Tuple2d t1, double alpha)
The first method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1 - alpha) * this + alpha * t1).
public boolean equals(Tuple2d t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of tuple t1 are equal to the corresponding data members in this tuple. The second method returns true if the Object t1 is of type Tuple2d and all of the data members of t1 are equal to the corresponding data members in this Tuple2d.
public boolean epsilonEquals(Tuple2d t1, double epsilon)
This method returns true if the L distance between this tuple and tuple t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
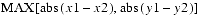public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two Tuple2d objects with identical data values (that is, equals(Tuple2d) returns true) will return the same hash number. Two objects with different data members may return the same hash number, although this is not likely.
public String toString()
This method returns a string that contains the values of this Tuple2d.

A.1.1.1 Point2d Class
The Point2d class extends Tuple2d. The Point2d is a two-element point represented by double-precision floating-point x,y coordinates.

Constructors
public Point2d(double x, double y)
public Point2d(double p[])
public Point2d(Point2d p1)
public Point2d(Point2f p1)
public Point2d(Tuple2d t1)
public Point2d(Tuple2f t1)
public Point2d()
Each of these seven constructors returns a new Point2d. The first constructor generates a Point2d from two double-precision floating-point numbers x and y. The second constructor generates a Point2d from the first two elements of array p. The third and fourth constructors generate a Point2d from the point p1. The fifth and sixth constructors generate a Point2d from the tuple t1. The final constructor generates a Point2d with the value of (0.0, 0.0).

Methods
public final double distanceSquared(Point2d p1)
public final double distance(Point2d p1)
The distanceSquared method computes the square of the Euclidean distance between this point and point p1 and returns the result. The distance method computes the Euclidean distance between this point and point p1 and returns the result.
public final double distanceL1(Point2d p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
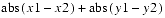public final double distanceLinf(Point2d p1)
This method computes the L distance between this point and point p1. The L distance is equal to

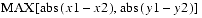
A.1.1.2 Vector2d Class
The Vector2d class extends Tuple2d. The Vector2f is a two-element vector represented by double-precision floating-point x,y coordinates.

Constructors
public Vector2d(double x, double y)
public Vector2d(double v[])
public Vector2d(Vector2d v1)
public Vector2d(Vector2f v1)
public Vector2d(Tuple2d t1)
public Vector2d(Tuple2f t1)
public Vector2d()
Each of these seven constructors returns a new Vector2d. The first constructor generates a Vector2d from two floating-point numbers x and y. The second constructor generates a Vector2d from the first two elements of array v. The third and fourth constructors generate a Vector2d from the vector v1. The fifth and sixth constructors generate a Vector2d from the specified tuple t1. The final constructor generates a Vector2d with the value of (0.0, 0.0).

Methods
public final double dot(Vector2d v1)
The dot method computes the dot product between this vector and vector v1 and returns the resulting value.
public final double lengthSquared()
public final double length()
The lengthSquared method computes the square of the length of the vector this and returns its length as a double-precision floating-point number. The length method computes the length of the vector this and returns its length as a double-precision floating-point number.
public final void normalize(Vector2d v1)
public final void normalize()
The first normalize method normalizes the vector v1 to unit length and places the result in this. The second normalize method normalizes the vector this and places the resulting unit vector back into this.
public final double angle(Vector2d v1)
This method returns the angle, in radians, between this vector and vector v1. The return value is constrained to the range [0, ].

A.1.2 Tuple2f Class
The Tuple2f class is a generic two-element tuple used mostly for specifying points and vectors made up of single-precision floating-point x,y coordinates.

Variables
The component values of a Tuple2f are directly accessible through the public variables x and y. To access the x component of a Tuple2f called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y component similarly.
public float x
public float y
The x and y coordinates, respectively.

Constructors
public Tuple2f(float x, float y)
public Tuple2f(float t[])
public Tuple2f(Tuple2f t1)
public Tuple2f(Tuple2d t1)
public Tuple2f()
Each of these five constructors returns a new Tuple2f. The first constructor generates a Tuple2f from two floating-point numbers x and y. The second constructor generates a Tuple2f from the first two elements of array t. The third and fourth constructors generate a Tuple2f from the tuple t1. The final constructor generates a Tuple2f with the value of (0.0, 0.0).

Methods
public final void set(float x, float y)
public final void set(float t[])
public final void set(Tuple2f t1)
punlic final void set(Tiple2d t1)
public final void get(float t[])
The set methods set the value of tuple this to the values provided. The get method copies the values of the elements of this tuple into the array t.
public final void add(Tuple2f t1, Tuple2f t2)
public final void add(Tuple2f t1)
public final void sub(Tuple2f t1, Tuple2f t2)
public final void sub(Tuple2f t1)
The first add method computes the element-by-element sum of tuples t1 and t2, placing the result in this. The second add method computes the element-by-element sum of this tuple and tuple t1, placing the result in this. The first sub method performs an element-by-element subtraction of tuple t2 from tuple t1 and places the result in this (this = t1 - t2). The second sub method performs an element-by-element subtraction of t1 from this and places the result in this (this = this - t1).
public final void negate(Tuple2f t1)
public final void negate()
The first negate method sets the values of this tuple to the negative of the values from tuple t1. The second negate method negates the tuple this and places the resulting tuple back into this.
public final void scale(float s, Tuple2f t1)
public final void scale(float s)
public final void scaleAdd(float s, Tuple2f t1)
public final void scaleAdd(float s, Tuple2f t1, Tuple2f t2)
The first scale method multiplies each element of the tuple t1 by the scale factor s and places the resulting scaled tuple into this. The second scale method multiplies each element of this tuple by the scale factor s and places the resulting scaled tuple into this. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into the tuple this (this = s*this + t1). The second scaleAdd method scales tuple t1 by the scale factor s, adds the result to tuple t2, then places the result into the tuple this (this = s*t1 + t2).
public final void absolute()
public final void absolute(Tuple2f t)
The first absolute method sets each component of this tuple to its absolute value. The second absolute method sets each component of this tuple to the absolute value of the corresponding component in tuple t.
public final void clamp(float min, float max)
public final void clamp(float min, float max, Tuple2f t)
public final void clampMin(float min)
public final void clampMin(float min, Tuple2f t)
public final void clampMax(float max)
public final void clampMax(float max, Tuple2f t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps the values from tuple t to the range [min, max] and assigns these clamped values to this tuple. The first clampMin method clamps each value of this tuple to the min parameter. The second clampMin method clamps each value of the tuple t and assigns these clamped values to this tuple. The first clampMax method clamps each value of this tuple to the max parameter. The second clampMax method clamps each value of tuple t to the max parameter and assigns these clamped values to this tuple. In each method the values of tuple t remain unchanged.
public final void interpolate(Tuple2f t1, Tuple2f t2, float  alpha)
public final void interpolate(Tuple2f t1, float alpha)
The first method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1 - alpha) * this + alpha * t1).
public boolean equals(Tuple2f t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of tuple t1 are equal to the corresponding data members in this tuple. The second method returns true if the Object t1 is of type Tuple2f and all of the data members of t1 are equal to the corresponding data members in this Tuple2f.
public boolean epsilonEquals(Tuple2f t1, float epsilon)
This method returns true if the L distance between this tuple and tuple t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
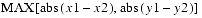public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two Tuple2f objects with identical data values (that is, equals(Tuple2f) returns true) will return the same hash number. Two objects with different data members may return the same hash number, although this is not likely.
public String toString()
This method returns a string that contains the values of this Tuple2f.

A.1.2.1 Point2f Class
The Point2f class extends Tuple2f. The Point2f is a two-element point represented by single-precision floating-point x,y coordinates.

Constructors
public Point2f(float x, float y)
public Point2f(float p[])
public Point2f(Point2f p1)
public Point2f(Point2d p1)
public Point2f(Tuple2f t1)
public Point2f(Tuple2f t1)
public Point2f()
Each of these seven constructors returns a new Point2f. The first constructor generates a Point2f from two floating-point numbers x and y. The second constructor generates a Point2f from the first two elements of array p. The third and fourth constructors generate a Point2f from the point p1. The fifth and sixth constructors generate a Point2f from the tuple t1. The final constructor generates a Point2f with the value of (0.0, 0.0).

Methods
public final float distanceSquared(Point2f p1)
public final float distance(Point2f p1)
The distanceSquared method computes the square of the Euclidean distance between this point and point p1 and returns the result. The distance method computes the Euclidean distance between this point and point p1 and returns the result.
public final float distanceL1(Point2f p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
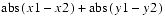public final float distanceLinf(Point2f p1)
This method computes the L distance between this point and point p1. The L distance is equal to

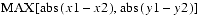
A.1.2.2 Vector2f Class
The Vector2f class extends Tuple2f. The Vector2f is a two-element vector represented by single-precision floating-point x,y coordinates.

Constructors
public Vector2f(float x, float y)
public Vector2f(float v[])
public Vector2f(Vector2f v1)
public Vector2f(Vector2d v1)
public Vector2f(Tuple2f t1)
public Vector2f(Tuple2d t1)
public Vector2f()
Each of these seven constructors returns a new Vector2f. The first constructor generates a Vector2f from two floating-point numbers x and y. The second constructor generates a Vector2f from the first two elements of array v. The third and fourth constructors generate a Vector2f from the vector v1. The fifth and sixth constructors generate a Vector2f from the specified tuple t1. The final constructor generates a Vector2f with the value of (0.0, 0.0).

Methods
public final float dot(Vector2f v1)
The dot method computes the dot product between this vector and vector v1 and returns the resulting value.
public final float lengthSquared()
public final float length()
The lengthSquared method computes the square of the length of the vector this and returns its length as a single-precision floating-point number. The length method computes the length of the vector this and returns its length as a single-precision floating-point number.
public final void normalize(Vector2f v1)
public final void normalize()
The first normalize method normalizes the vector v1 to unit length and places the result in this. The second normalize method normalizes the vector this and places the resulting unit vector back into this.
public final float angle(Vector2f v1)
This method returns the angle, in radians, between this vector and vector v1. The return value is constrained to the range [0, ].

A.1.2.3 TexCoord2f Class
The TexCoord2f class is a subset of Tuple2f. The TexCoord2f is a two-element vector represented by single-precision floating-point x,y coordinates.

Constructors
public TexCoord2f(float x, float y)
public TexCoord2f(float v[])
public TexCoord2f(TexCoord2f v1)
public TexCoord2f(Tuple2f t1)
public TexCoord2f()
Each of these five constructors returns a new TexCoord2f. The first constructor generates a TexCoord2f from two floating-point numbers x and y. The second constructor generates a TexCoord2f from the first two elements of array v. The third constructor generates a TexCoord2f from the TexCoord2f v1. The fourth constructor generates a TexCoord2f from the Tuple2f t1. The final constructor generates a TexCoord2f with the value of (0.0, 0.0).

A.1.3 Tuple3b Class
The Tuple3b class is used for colors. This class represents a three-byte tuple. Note that Java defines a byte as a signed integer in the range [-128, 127]. However, colors are more typically represented by values in the range [0, 255]. Java 3D recognizes this and, in those cases where Tuple3b is used to represent color, treats the bytes as if the range were [0, 255]-in other words, as if the bytes were unsigned. Values greater than 127 can be assigned to a byte variable using a type cast. For example,
byteVariable = (byte) intValue;    // intValue can be > 127
If intValue is greater than 127, then byteVariable will be negative. The correct value will be extracted when it is used (by masking off the upper bits).

Variables
The component values of a Tuple3b are directly accessible through the public variables x, y, and z. To access the x (red) component of a Tuple3b called myColor, a programmer would write myColor.x. The programmer would access the y (green) and z (blue) components similarly.
public byte x
public byte y
public byte z
The red, green, and blue values, respectively.

Constructors
public Tuple3b(byte b1, byte b2, byte b3)
public Tuple3b(byte t[])
public Tuple3b(Tuple3b t1)
public Tuple3b()
Each of these four constructors returns a new Tuple3b. The first constructor generates a Tuple3b from three bytes b1, b2, and b3. The second constructor generates a Tuple3b from the first three elements of array t. The third constructor generates a Tuple3b from the byte-precision Tuple3b t1. The final constructor generates a Tuple3b with the value of (0.0, 0.0, 0.0).

Methods
public String toString()
This method returns a string that contains the values of this Tuple3b.
public final void set(byte t[])
public final void set(Tuple3b t1)
public final void get(byte t[])
public final void get(Tuple3b t1)
The first set method sets the values of the x, y, and z data members of this Tuple3b to the values in the array t of length three. The second set method sets the values of the x, y, and z data members of this Tuple3b to the values in the argument tuple t1. The first get method places the values of the x, y, and z components of this Tuple3b into the array t of length three. The second get method places the values of the x, y, and z components of this Tuple3b into the tuple t1.
public boolean equals(Tuple3b t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Tuple3b t1 are equal to the corresponding data members in this tuple. The second method returns true if the Object t1 is of type Tuple3b and all of the data members of t1 are equal to the corresponding data members in this Tuple3b.
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple3b objects with identical data values (that is, equals(Tuple3b) returns true) will return the same hash number. Two tuples with different data members may return the same hash value, although this is not likely.

A.1.3.1 Color3b Class
The Color3b class extends Tuple3b and represents three-byte color values.

Constructors
public Color3b(byte c1, byte c2, byte c3)
public Color3b(byte c[])
public Color3b(Color3b c1)
public Color3b(Tuple3b t1)
public Color3b(Color color)
public Color3b()
Each of these five constructors returns a new Color3b. The first constructor generates a Color3b from three bytes c1, c2, and c3. The second constructor generates a Color3b from the first three elements of array c. The third constructor generates a Color3b from the byte-precision Color3b c1. The fourth constructor generates a Color3b from the tuple t1. The fifth constructor generates a Color3b from the specified AWT Color object. The final constructor generates a Color3b with the value of (0.0, 0.0, 0.0).

Methods
public final void set(Color color)
public final Color get()
The set method sets the R,G,B values of this Color3b object to those of the specified AWT Color object. The get method returns a new AWT Color object initialized with the R,G,B values of this Color3b object.

A.1.4 Tuple3d Class
The Tuple3d class is a generic three-element tuple represented by double-precision floating-point x, y, and z coordinates.

Variables
The component values of a Tuple3d are directly accessible through the public variables x, y, and z. To access the x component of a Tuple3d called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y and z components similarly.
public double x
public double y
public double z
The x, y, and z coordinates, respectively.

Constructors
public Tuple3d(double x, double y, double z)
public Tuple3d(double t[])
public Tuple3d(Tuple3d t1)
public Tuple3d(Tuple3f t1)
public Tuple3d()
Each of these five constructors returns a new Tuple3d. The first constructor generates a Tuple3d from three floating-point numbers x, y, and z. The second constructor generates a Tuple3d from the first three elements of array t. The third constructor generates a Tuple3d from the double-precision Tuple3d t1. The fourth constructor generates a Tuple3d from the single-precision Tuple3f t1. The final constructor generates a Tuple3d with the value of (0.0, 0.0, 0.0).

Methods
public final void set(double x, double y, double z)
public final void set(double t[])
public final void set(Tuple3d t1)
public final void set(Tuple3f t1)
public final void get(double t[])
public final void get(Tuple3d t)
The four set methods set the value of tuple this to the values specified or to the values of the specified vectors. The two get methods copy the x, y, and z values into the array t of length three.
public final void add(Tuple3d t1, Tuple3d t2)
public final void add(Tuple3d t1)
public final void sub(Tuple3d t1, Tuple3d t2)
public final void sub(Tuple3d t1)
The first add method computes the element-by-element sum of tuples t1 and t2 and places the result in this. The second add method computes the element-by-element sum of this tuple and tuple t1 and places the result into this. The first sub method performs an element-by-element subtraction of tuple t2 from tuple t1 and places the result in this (this = t1 - t2). The second sub method performs an element-by-element subtraction of tuple t1 from this tuple and places the result in this (this = this - t1).
public final void negate(Tuple3d t1)
public final void negate()
The first negate method sets the values of this tuple to the negative of the values from tuple t1. The second negate method negates the tuple this and places the resulting tuple back into this.
public final void scaleAdd(double s, Tuple3f t1)
A deprecated method. See method below.
public final void scale(double s, Tuple3d t1)
public final void scale(double s)
public final void scaleAdd(double s, Tuple3d t1)
public final void scaleAdd(double s, Tuple3d t1, Tuple3d t2)
The first scale method multiplies each element of the tuple t1 by the scale factor s and places the resulting scaled tuple into this. The second scale method multiplies each element of this tuple by the scale factor s and places the resulting scaled tuple back into this. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into tuple this (this = s*this + t1). The second scaleAdd method scales the tuple t1 by the scale factor s, adds the result to the tuple t2, and places the result into the tuple this (this = s*t1 + t2).
public String toString()
This method returns a string that contains the values of this Tuple3d. The form is (x, y, z).
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple3d objects with identical data values (that is, equals(Tuple3d) returns true) will return the same hash number. Two tuples with different data members may return the same hash value, although this is not likely.
public boolean equals(Tuple3d v1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Tuple3d v1 are equal to the corresponding data members in this Tuple3d. The second method returns true if the Object t1 is of type Tuple3d and all of the data members of t1 are equal to the corresponding data members in this Tuple3d.
public boolean epsilonEquals(Tuple3d t1, double epsilon)
This method returns true if the L distance between this tuple and tuple t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
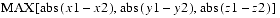public final void absolute()
public final void absolute(Tuple3d t)
The first absolute method sets each component of this tuple to its absolute value. The second absolute method sets each component of this tuple to the absolute value of the corresponding component in tuple t.
public final void clamp(float min, float max)
public final void clamp(float min, float max, Tuple3d t)
public final void clampMin(float min)
public final void clampMin(float min, Tuple3d t)
public final void clampMax(float max)
public final void clampMax(float max, Tuple3d t)
Deprecated methods. See the next six methods.
public final void clamp(double min, double max)
public final void clamp(double min, double max, Tuple3d t)
public final void clampMin(double min)
public final void clampMin(double min, Tuple3d t)
public final void clampMax(double max)
public final void clampMax(double max, Tuple3d t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps the values from tuple t to the range [min, max] and assigns these clamped values to this tuple. The first clampMin method clamps each value of this tuple to the min parameter. The second clampMin method clamps each value of the tuple t and assigns these clamped values to this tuple. The first clampMax method clamps each value of this tuple to the max parameter. The second clampMax method clamps each value of tuple t to the max parameter and assigns these clamped values to this tuple. In each method, the values of tuple t remain unchanged.
public final void interpolate(Tuple3d t1, Tuple3d t2, float  alpha)
public final void interpolate(Tuple3d t1, float alpha)
Deprecated methods. See the next two methods.
public final void interpolate(Tuple3d t1, Tuple3d t2, double  alpha)
public final void interpolate(Tuple3d t1, double alpha)
The first interpolate method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second interpolate method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1 - alpha) * this + alpha * t1).

A.1.4.1 Point3d Class
The Point3d class extends Tuple3d. The Point3d is a three-element point represented by double-precision floating-point x, y, and z coordinates.

Constructors
public Point3d(double x, double y, double z)
public Point3d(double p[])
public Point3d(Point3d p1)
public Point3d(Point3f p1)
public Point3d(Tuple3d t1)
public Point3d(Tuple3f t1)
public Point3d()
Each of these seven constructors returns a new Point3d. The first constructor generates a Point3d from three floating-point numbers x, y, and z. The second constructor generates a Point3d from the first three elements of array p. The third constructor generates a Point3d from the double-precision Point3d p1. The fourth constructor generates a Point3d from the single-precision Point3f p1. The fifth and sixth constructors generate a Point3d from the tuple t1. The final constructor generates a Point3d with the value of (0.0, 0.0, 0.0).

Methods
public final double distanceSquared(Point3d p1)
public final double distance(Point3d p1)
The distanceSquared method computes the square of the Euclidean distance between this Point3d and the Point3d p1 and returns the result. The distance method computes the Euclidean distance between this Point3d and the Point3d p1 and returns the result.
public final double distanceL1(Point3d p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
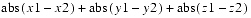public final double distanceLinf(Point3d p1)
This method computes the L distance between this point and point p1. The L distance is equal to
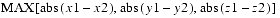public final void project(Point4d p1)
This method multiplies each of the x, y, and z components of the Point4d parameter p1 by 1/w and places the projected values into this point.

A.1.4.2 Vector3d Class
The Vector3d class extends Tuple3d. The Vector3d is a three-element vector represented by double-precision floating-point x, y, and z coordinates. If this value represents a normal, it should be normalized.

Constructors
public Vector3d(double x, double y, double z)
public Vector3d(double v[])
public Vector3d(Vector3d v1)
public Vector3d(Vector3f v1)
public Vector3d(Tuple3d t1)
public Vector3d(Tuple3f t1)
public Vector3d()
Each of these seven constructors returns a new Vector3d. The first constructor generates a Vector3d from three floating-point numbers x, y, and z. The second constructor generates a Vector3d from the first three elements of array v. The third constructor generates a Vector3d from the double-precision vector v1. The fourth constructor generates a Vector3d from the single-precision vector v1. The fifth and sixth constructors generate a Vector3d from the tuple t1. The final constructor generates a Vector3d with the value of (0.0, 0.0, 0.0).

Methods
public final void cross(Vector3d v1, Vector3d v2)
The cross method computes the vector cross-product of vectors v1 and v2 and places the result in this.
public final void normalize(Vector3d v1)
public final void normalize()
The first normalize method normalizes the vector v1 to unit length and places the result in this. The second normalize method normalizes the vector this and places the resulting unit vector back into this.
public final double dot(Vector3d v1)
The dot method returns the dot product of this vector and vector v1.
public final double lengthSquared()
public final double length()
The lengthSquared method returns the squared length of this vector. The length method returns the length of this vector.
public final double angle(Vector3d v1)
This method returns the angle, in radians, between this vector and the vector v1 parameter. The return value is constrained to the range [0, ].

A.1.5 Tuple3f Class
The Tuple3f class is a generic three-element tuple represented by single-precision floating-point x, y, and z coordinates.

Variables
The component values of a Tuple3f are directly accessible through the public variables x, y, and z. To access the x component of a Tuple3f called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y and z components similarly.
public float x
public float y
public float z
The x, y, and z coordinates, respectively.

Constructors
public Tuple3f(float x, float y, float z)
public Tuple3f(float t[])
public Tuple3f(Tuple3d t1)
public Tuple3f(Tuple3f t1)
public Tuple3f()
Each of these five constructors returns a new Tuple3f. The first constructor generates a Tuple3f from three floating-point numbers x, y, and z. The second constructor generates a Tuple3f from the first three elements of array t. The third constructor generates a Tuple3f from the double-precision Tuple3d t1. The fourth constructor generates a Tuple3f from the single-precision Tuple3f t1. The final constructor generates a Tuple3f with the value of (0.0, 0.0, 0.0).

Methods
public String toString()
This method returns a string that contains the values of this Tuple3f.
public final void set(float x, float y, float z)
public final void set(float t[])
public final void set(Tuple3f t1)
public final void set(Tuple3d t1)
public final void get(float t[])
public final void get(Tuple3f t)
The four set methods set the value of vector this to the coordinates provided or to the values of the vectors provided. The first get method gets the value of this vector and copies the values into the array t. The second get method gets the value of this vector and copies the values into tuple t.
public final void add(Tuple3f t1, Tuple3f t2)
public final void add(Tuple3f t1)
public final void sub(Tuple3f t1, Tuple3f t2)
public final void sub(Tuple3f t1)
The first add method computes the element-by-element sum of tuples t1 and t2, placing the result in this. The second add method computes the element-by-element sum of this and tuple t1 and places the result in this. The first sub method performs an element-by-element subtraction of tuple t2 from tuple t1 and places the result in this (this = t1 - t2). The second sub method performs an element-by-element subtraction of tuple t1 from this tuple and places the result into this (this = this - t1).
public final void negate(Tuple3f t1)
public final void negate()
The first negate method sets the values of this tuple to the negative of the values from tuple t1. The second negate method negates the vector this and places the resulting tuple back into this.
public final void scale(float s, Tuple3f t1)
public final void scale(float s)
public final void scaleAdd(float s, Tuple3f t1)
public final void scaleAdd(float s, Tuple3f t1, Tuple3f t2)
The first scale method multiplies each element of the vector t1 by the scale factor s and places the resulting scaled vector into this. The second scale method multiples the vector this by the scale factor s and replaces this with the scaled value. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into tuple this (this = s*this + t1). The second scaleAdd method scales the tuple t1 by the scale factor s, adds the result to the tuple t2, and places the result into the tuple this (this = s*t1 + t2).
public boolean equals(Tuple3f t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of tuple t1 are equal to the corresponding data members in this Tuple3f. The second method returns true if the Object t1 is of type Tuple3f and all of the data members of t1 are equal to the corresponding data members in this Tuple3f.
public boolean epsilonEquals(Tuple3f t1, float epsilon)
This method returns true if the L distance between this tuple and tuple t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
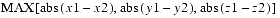public final void absolute()
public final void absolute(Tuple3f t)
The first absolute method sets each component of this tuple to its absolute value. The second absolute method sets each component of this tuple to the absolute value of the corresponding component in tuple t.
public final void clamp(float min, float max)
public final void clamp(float min, float max, Tuple3f t)
public final void clampMin(float min)
public final void clampMin(float min, Tuple3f t)
public final void clampMax(float max)
public final void clampMax(float max, Tuple3f t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps the values from tuple t to the range [min, max] and assigns these clamped values to this tuple. The first clampMin method clamps each value of this tuple to the min parameter. The second clampMin method clamps each value of the tuple t and assigns these clamped values to this tuple. The first clampMax method clamps each value of this tuple to the max parameter. The second clampMax method clamps each value of tuple t to the max parameter and assigns these clamped values to this tuple. In each method the values of tuple t remain unchanged.
public final void interpolate(Tuple3f t1, Tuple3f t2, float  alpha)
public final void interpolate(Tuple3f t1, float alpha)
The first method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1-alpha) * this + alpha * t1).
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple3f objects with identical data values (that is, equals(Tuple3f) returns true) will return the same hash number. Two tuples with different data members may return the same hash value, although this is not likely.

A.1.5.1 Point3f Class
The Point3f class extends Tuple3f. The Point3f is a three-element point represented by single-precision floating-point x, y, and z coordinates.

Constructors
public Point3f(float x, float y, float z)
public Point3f(float p[])
public Point3f(Point3d p1)
public Point3f(Point3f p1)
public Point3f(Tuple3d t1)
public Point3f(Tuple3f t1)
public Point3f()
Each of these seven constructors returns a new Point3f. The first constructor generates a point from three floating-point numbers x, y, and z. The second constructor (Point3f(float p[]) generates a point from the first three elements of array p. The third constructor generates a point from the double-precision point p1. The fourth constructor generates a point from the single-precision point p1. The fifth and sixth constructors generate a Point3f from the tuple t1. The final constructor generates a point with the value of (0.0, 0.0, 0.0).

Methods
public final float distance(Point3f p1)
public final float distanceSquared(Point3f p1)
The distance method computes the Euclidean distance between this point and the point p1 and returns the result. The distanceSquared method computes the square of the Euclidean distance between this point and the point p1 and returns the result.
public final float distanceL1(Point3f p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
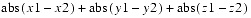public final float distanceLinf(Point3f p1)
This method computes the L distance between this point and point p1. The L distance is equal to
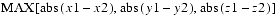public final void project(Point4f p1)
This method multiplies each of the x, y, and z components of the Point4f parameter p1 by 1/w and places the projected values into this point.

A.1.5.2 Vector3f Class
The Vector3f class extends Tuple3f. The Vector3f is a three-element vector represented by single-precision floating-point x, y, and z coordinates.

Constructors
public Vector3f(float x, float y, float z)
public Vector3f(float v[])
public Vector3f(Vector3d v1)
public Vector3f(Vector3f v1)
public Vector3f(Tuple3d t1)
Public Vector3f(Tuple3f t1)
public Vector3f()
Each of these seven constructors returns a new Vector3f. The first constructor generates a Vector3f from three floating-point numbers x, y, and z. The second constructor generates a Vector3f from the first three elements of array v. The third constructor generates a Vector3f from the double-precision Vector3d v1. The fourth constructor generates a Vector3f from the single-precision Vector3f v1. The fifth and sixth constructors generate a Vector3f from the tuple t1. The final constructor generates a Vector3f with the value of (0.0, 0.0, 0.0).

Methods
public final float length()
public final float lengthSquared()
The length method computes the length of the vector this and returns its length as a single-precision floating-point number. The lengthSquared method computes the square of the length of the vector this and returns its length as a single-precision floating-point number.
public final void cross(Vector3f v1, Vector3f v2)
The cross method computes the vector cross-product of v1 and v2 and places the result in this.
public final float dot(Vector3f v1)
The dot method computes the dot product between this vector and the vector v1 and returns the resulting value.
public final void normalize(Vector3f v1)
public final void normalize()
The first normalize method normalizes the vector v1 to unit length and places the result in this. The second normalize method normalizes the vector this and places the resulting unit vector back into this.
public final float angle(Vector3f v1)
This method returns the angle, in radians, between this vector and the vector parameter. The return value is constrained to the range [0, ].

A.1.5.3 TexCoord3f Class
The TexCoord3f class extends Tuple3f. The TexCoord3f is a three-element texture coordinate represented by single-precision floating-point x, y, and z coordinates.

Constructors
public TexCoord3f(float x, float y, float z)
public TexCoord3f(float v[])
public TexCoord3f(TexCoord3f v1)
public TexCoord3f(Tuple3d t1)
public TexCoord3f(Tuple3f t1)
public TexCoord3f()
Each of these six constructors returns a new TexCoord3f. The first constructor generates a texture coordinate from three floating-point numbers x, y, and z. The second constructor generates a texture coordinate from the first three elements of array v. The third constructor generates a texture coordinate from the single-precision TexCoord3f v1. The fourth and fifth constructors generate a texture coordinate from tuple t1. The final constructor generates a texture coordinate with the value of (0.0, 0.0, 0.0).

A.1.5.4 Color3f Class
The Color3f class extends Tuple3f. The Color3f is a three-element color value represented by single-precision floating-point x, y, and z values. The x, y, and z values represent the red, blue, and green color values, respectively. Color components should be in the range [0.0, 1.0].

Constructors
public Color3f(float x, float y, float z)
public Color3f(float v[])
public Color3f(Color3f v1)
public Color3f(Tuple3d t1)
public Color3f(Tuple3f t1)
public Color3f(Color color)
public Color3f()
Each of these six constructors returns a new Color3f. The first constructor generates a Color3f from three floating-point numbers x, y, and z. The second constructor (Color3f(float v[]) generates a Color3f from the first three elements of array v. The third constructor generates a Color3f from the single-precision color v1. The fourth and fifth constructors generate a Color3f from the tuple t1. The sixth constructor generates a Color3f from the specified AWT Color object. The final constructor generates a Color3f with the value of (0.0, 0.0, 0.0).

Methods
public final void set(Color color)
public final Color get()
The set method sets the R,G,B values of this Color3f object to those of the specified AWT Color object. The get method returns a new AWT Color object initialized with the R,G,B values of this Color3f object.

A.1.6 Tuple3i Class
The Tuple3i class is a generic three-element tuple represented by signed integer x,y,z coordinates.

Variables
The component values of a Tuple3i are directly accessible through the public variables x, y, and z. To access the x component of a Tuple3i called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y and z components similarly.
public int x
public int y
public int z
The x, y, and z coordinates, respectively.

Constructors
public Tuple3i(int x, int y, int z)
public Tuple3i(int[] t)
public Tuple3i(Tuple3i t1)
public Tuple3i()
Each of these four constructors returns a new Tuple3i. The first constructor generates a Tuple3i from the specified x, y, and z coordinates. The second constructor generates a Tuple3i from the array of length 3. The third constructor generates a Tuple3i from the specified Tuple3i. The final constructor generates a Tuple3i with the value of (0,0,0).

Methods
public String toString()
This method returns a string that contains the values of this Tuple3i.
public final void set(int x, int y, int z)
public final void set(int[] t)
public final void set(Tuple3i t1)
public final void get(int[] t)
public final void get(Tuple3i t)
The first set method sets the value of this tuple to the specified x, y, and z coordinates. The second set method sets the value of this tuple to the specified coordinates in the array of length 3. The third set method sets the value of this tuple to the value of tuple t1. The first get method copies the values of this tuple into the array t. The second get method copies the values of this tuple into the tuple t.
public final void add(Tuple3i t1, Tuple3i t2)
public final void add(Tuple3i t1)
The first method sets the value of this tuple to the sum of tuples t1 and t2. The second method sets the value of this tuple to the sum of itself and t1.
public final void sub(Tuple3i t1, Tuple3i t2)
public final void sub(Tuple3i t1)
The first method sets the value of this tuple to the difference of tuples t1 and t2 (this = t1 - t2). The second method sets the value of this tuple to the difference of itself and t1 (this = this - t1).
public final void negate(Tuple3i t1)
public final void negate()
The first method sets the value of this tuple to the negation of tuple t1. The second method negates the value of this tuple in place.
public final void scale(int s, Tuple3i t1)
public final void scale(int s)
The first method sets the value of this tuple to the scalar multiplication of tuple t1. The second method sets the value of this tuple to the scalar multiplication of the scale factor with this.
public final void scaleAdd(int s, Tuple3i t1, Tuple3i t2)
public final void scaleAdd(int s, Tuple3i t1)
The first method sets the value of this tuple to the scalar multiplication of tuple t1 plus tuple t2 (this = s*t1 + t2). The second method sets the value of this tuple to the scalar multiplication of itself and then adds tuple t1 (this = s*this + t1).
public boolean equals(Object t1)
This method returns true if the Object t1 is of type Tuple3i and all of the data members of t1 are equal to the corresponding data members in this Tuple3i.
public final void clamp(int min, int max, Tuple3i t)
public final void clamp(int min, int max)
The first method clamps the tuple parameter to the range [low, high] and places the values into this tuple. The second method clamps this tuple to the range [low, high].
public final void clampMin(int min, Tuple3i t)
public final void clampMin(int min)
public final void clampMax(int max, Tuple3i t)
public final void clampMax(int max)
The first method clamps the minimum value of the tuple parameter to the min parameter and places the values into this tuple. The second method clamps the minimum value of this tuple to the min parameter. The third method clamps the maximum value of the tuple parameter to the max parameter and places the values into this tuple. The final method clamps the maximum value of this tuple to the max parameter.
public final void absolute(Tuple3i t)
public final void absolute()
The first method sets each component of the tuple parameter to its absolute value and places the modified values into this tuple. The second method sets each component of this tuple to its absolute value.
public int hashCode()
This method returns a hash code value based on the data values in this object. Two different Tuple3i objects with identical data values (that is, Tuple3i.equals returns true) will return the same hash code value. Two objects with different data members may return the same hash value, although this is not likely.

A.1.6.1 Point3i Class
The Point3i class extends Tuple3i. The Point3i is a three-element point represented by signed integer x,y,z coordinates.

Constructors
public Point3i(int x, int y, int z)
public Point3i(int[] t)
public Point3i(Tuple3i t1
public Point3i()
Each of these four constructors returns a new Point3i. The first constructor generates a Point3i from the specified x, y, and z coordinates. The second constructor generates a Point3i from the array of length 3. The third constructor generates a Point3i from the specified Tuple3i. The final constructor generates a Point3i with the value of (0,0,0).

A.1.7 Tuple4b Class
The Tuple4b class represents four-byte tuples. Note that Java defines a byte as a signed integer in the range [-128, 127]. However, colors are more typically represented by values in the range [0, 255]. Java 3D recognizes this and, in those cases where Tuple4b is used to represent color, treats the bytes as if the range were [0, 255]-in other words, as if the bytes were unsigned. Values greater than 127 can be assigned to a byte variable using a type cast. For example,
byteVariable = (byte) intValue;    // intValue can be > 127
If intValue is greater than 127, then byteVariable will be negative. The correct value will be extracted when it is used (by masking off the upper bits).

Variables
The component values of a Tuple4b are directly accessible through the public variables x, y, z, and w. The x, y, z, and w values represent the red, green, blue, and alpha values, respectively. To access the x (red) component of a Tuple4b called backgroundColor, a programmer would write backgroundColor.x. The programmer would access the y (green), z (blue), and w (alpha) components similarly.
public byte x
public byte y
public byte z
public byte w
The red, green, blue, and alpha values, respectively.

Constructors
public Tuple4b(byte b1, byte b2, byte b3, byte b4)
public Tuple4b(byte t[])
public Tuple4b(Tuple4b t1)
public Tuple4b()
Each of these four constructors returns a new Tuple4b. The first constructor generates a Tuple4b from four bytes b1, b2, b3, and b4. The second constructor (Tuple4b(byte t[]) generates a Tuple4b from the first four elements of array t. The third constructor generates a Tuple4b from the byte-precision Tuple4b t1. The final constructor generates a Tuple4b with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public String toString()
This method returns a string that contains the values of this Tuple4b.
public final void set(byte b[])
public final void set(Tuple4b t1)
public final void get(byte b[])
public final void get(Tuple4b t1)
The first set method sets the value of the data members of this Tuple4b to the value of the array b. The second set method sets the value of the data members of this Tuple4b to the value of the argument tuple t1. The first get method places the values of the x, y, z, and w components of this Tuple4b into the byte array b. The second get method places the values of the x, y, z, and w components of this Tuple4b into the Tuple4b t1.
public boolean equals(Tuple4b t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Tuple4b t1 are equal to the corresponding data members in this Tuple4b. The second method returns true if the Object t1 is of type Tuple4b and all of the data members of t1 are equal to the corresponding data members in this Tuple4b.
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple4b objects with identical data values (that is, equals(Tuple4b) returns true) will return the same hash number. Two Tuple4b objects with different data members may return the same hash value, although this is not likely.

A.1.7.1 Color4b Class
The Color4b class extends Tuple4b. The Color4b is a four-byte color value (red, green, blue, and alpha).

Constructors
public Color4b(byte b1, byte b2, byte b3, byte b4)
public Color4b(byte c[])
public Color4b(Color4b c1)
public Color4b(Tuple4b t1)
public Color4b(Color color)
public Color4b()
Each of these five constructors returns a new Color4b. The first constructor generates a Color4b from four bytes-b1, b2, b3, and b4. The second constructor generates a Color4b from the first four elements of byte array c. The third constructor generates a Color4b from the byte-precision Color4b c1. The fourth constructor generates a Color4b from the tuple t1. The fifth constructor generates a Color4b from the specified AWT Color object. The final constructor generates a Color4b with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Color color)
public final Color get()
The set method sets the R,G,B,A values of this Color4b object to those of the specified AWT Color object. The get method returns a new AWT Color object initialized with the R,G,B,A values of this Color4b object.

A.1.8 Tuple4d Class
The Tuple4d class represents a four-element tuple represented by double-precision floating-point x, y, z, and w coordinates.

Variables
The component values of a Tuple4d are directly accessible through the public variables x, y, z, and w. To access the x component of a Tuple4d called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y, z, and w components similarly.
public double x
public double y
public double z
public double w
The x, y, z, and w coordinates, respectively.

Constructors
public Tuple4d(double x, double y, double z, double w)
public Tuple4d(double t[])
public Tuple4d(Tuple4d t1)
public Tuple4d(Tuple4f t1)
public Tuple4d()
Each of these five constructors returns a new Tuple4d. The first constructor generates a Tuple4d from four floating-point numbers x, y, z, and w. The second constructor (Tuple4d(double t[]) generates a Tuple4d from the first four elements of array t. The third constructor generates a Tuple4d from the double-precision tuple t1. The fourth constructor generates a Tuple4d from the single-precision tuple t1. The final constructor generates a Tuple4d with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(double x, double y, double z, double w)
public final void set(double t[])
public final void set(Tuple4d t1)
public final void set(Tuple4f t1)
public final void get(double t[])
public final void get(Tuple4d t)
These methods set the value of the tuple this to the values specified or to the values of the specified tuples. The first get method retrieves the value of this tuple and places it into the array t of length four, in x, y, z, w order. The second get method retrieves the value of this tuple and places it into tuple t.
public final void add(Tuple4d t1, Tuple4d t2)
public final void add(Tuple4d t1)
public final void sub(Tuple4d t1, Tuple4d t2)
public final void sub(Tuple4d t1)
The first add method computes the element-by-element sum of the tuple t1 and the tuple t2, placing the result in this. The second add method computes the element-by-element sum of this tuple and the tuple t1 and places the result in this. The first sub method performs an element-by-element subtraction of tuple t2 from tuple t1 and places the result in this. The second sub method performs an element-by-element subtraction of tuple t1 from this tuple and places the result in this.
public final void negate(Tuple4d t1)
public final void negate()
The first negate method sets the values of this tuple to the negative of the values from tuple t1. The second negate method negates the tuple this and places the resulting tuple back into this.
public final void scaleAdd(float s, Tuple4d t1)
Deprecated method. See the following method.
public final void scale(double s, Tuple4d t1)
public final void scale(double s)
public final void scaleAdd(double s, Tuple4d t1)
public final void scaleAdd(double s, Tuple4d t1, Tuple4d t2)
The first scale method multiplies each element of the tuple t1 by the scale factor s and places the resulting scaled tuple into this. The second scale method multiples the tuple this by the scale factor s and replaces this with the scaled value. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into tuple this (this = s*this + t1). The second scaleAdd method scales the tuple t1 by the scale factor s, adds the result to the tuple t2, and places the result into the tuple this (this = s*t1 + t2).
public void interpolate(Tuple4d t1, Tuple4d t2, float alpha)
public void interpolate(Tuple4d t1, float alpha)
Deprecated methods. See the following two methods.
public void interpolate(Tuple4d t1, Tuple4d t2, double alpha)
public void interpolate(Tuple4d t1, double alpha)
The first interpolate method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second interpolate method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1 - alpha) * this + alpha * t1).
public String toString()
This method returns a string that contains the values of this tuple. The form is (x, y, z, w).
public boolean equals(Tuple4d v1)
public boolean equals(Object t1)
The first method returns true if all of the data members of tuple v1 are equal to the corresponding data members in this tuple. The second method returns true if the Object t1 is of type Tuple4d and all of the data members of t1 are equal to the corresponding data members in this Tuple4d.
public boolean epsilonEquals(Tuple4d t1, double epsilon)
This method returns true if the L distance between this Tuple4d and Tuple4d t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
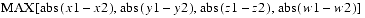public final void absolute()
public final void absolute(Tuple4d t)
The first absolute method sets each component of this tuple to its absolute value. The second absolute method sets each component of this tuple to the absolute value of the corresponding component in tuple t.
public final void clamp(float min, float max)
public final void clamp(float min, float max, Tuple4d t)
public final void clampMin(float min)
public final void clampMin(float min, Tuple4d t)
public final void clampMax(float max)
public final void clampMax(float max, Tuple4d t)
Deprecated methods. See the following six methods.
public final void clamp(double min, double max)
public final void clamp(double min, double max, Tuple4d t)
public final void clampMin(double min)
public final void clampMin(double min, Tuple4d t)
public final void clampMax(double max)
public final void clampMax(double max, Tuple4d t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps this tuple to the range [min, max] and places the values into tuple t. The first clampMin method clamps the minimum value of this tuple to the min parameter. The second clampMin method clamps the minimum value of this tuple to the min parameter and places the values into the tuple t. The first clampMax method clamps the maximum value of this tuple to the max parameter. The second clampMax method clamps the maximum value of this tuple to the max parameter and places the values into the tuple t.
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple4d objects with identical data values (that is, equals(Tuple4d) returns true) will return the same hash number. Two Tuple4d objects with different data members may return the same hash value, although this is not likely.

A.1.8.1 Point4d Class
The Point4d class extends Tuple4d. The Point4d is a four-element point represented by double-precision floating-point x, y, z, and w coordinates.

Constructors
public Point4d(double x, double y, double z, double w)
public Point4d(double p[])
public Point4d(Point4d p1)
public Point4d(Point4f p1)
public Point4d(Tuple4d t1)
public Point4d(Tuple4f t1)
public Point4d(Tuple3d t1)
public Point4d()
Each of these eight constructors returns a new Point4d. The first constructor generates a Point4d from four floating-point numbers x, y, z, and w. The second constructor (Point4d(double p[]) generates a Point4d from the first four elements of array p. The third constructor generates a Point4d from the double-precision point p1. The fourth constructor generates a Point4d from the single-precision point p1. The fifth and sixth constructors generate a Point4d from tuple t1. The seventh constructor generates a Point4d from the specified Tuple3d-the w component of this point is set to 1. The final constructor generates a Point4d with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Tuple3d t1)
This method sets the x, y, and z components of this point to the corresponding components of tuple t1. The w component of this point is set to 1.
public final double distance(Point4d p1)
public final double distanceSquared(Point4d p1)
The distance method computes the Euclidean distance between this point and the point p1 and returns the result. The distanceSquared method computes the square of the Euclidean distance between this point and the point p1 and returns the result.
public final double distanceL1(Point4d p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
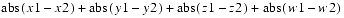public final double distanceLinf(Point4d p1)
This method computes the L distance between this point and point p1. The L distance is equal to
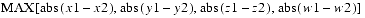public final void project(Point4d p1)
This method multiplies each of the x, y, and z components of the point p1 by , places the projected values into this point, and places a 1 into the w parameter of this point.

A.1.8.2 Vector4d Class
The Vector4d class extends Tuple4d. The Vector4d is a four-element vector represented by double-precision floating-point x, y, z, and w coordinates.

Constructors
public Vector4d(double x, double y, double z, double w)
public Vector4d(double v[])
public Vector4d(Vector4d v1)
public Vector4d(Vector4f v1)
public Vector4d(Tuple4d t1)
public Vector4d(Tuple4f t1)
public Vector4d(Tuple3d t1)
public Vector4d()
Each of these eight constructors returns a new Vector4d. The first constructor generates a Vector4d from four floating-point numbers x, y, z, and w. The second constructor generates a Vector4d from the first four elements of array v. The third constructor generates a Vector4d from the double-precision Vector4d v1. The fourth constructor generates a Vector4d from the single-precision Vector4f v1. The fifth and sixth constructors generate a Vector4d from tuple t1. The seventh constructor generates a Vector4d from the specified Tuple3d-the w component of this vector is set to 0. The final constructor generates a Vector4d with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Tuple3d t1)
This method sets the x, y, and z components of this vector to the corresponding components of tuple t1. The w component of this vector is set to 0.
public final double length()
public final double lengthSquared()
The length method computes the length of the vector this and returns its length as a double-precision floating-point number. The lengthSquared method computes the square of the length of the vector this and returns its length as a double-precision floating-point number.
public final void dot(Vector4d v1)
This method returns the dot product of this vector and vector v1.
public final void normalize(Vector4d v1)
public final void normalize()
The first normalize method normalizes the vector v1 to unit length and places the result in this. The second normalize method normalizes the vector this and places the resulting unit vector back into this.
public final double angle(Vector4d v1)
This method returns the (four-space) angle, in radians, between this vector and the vector v1 parameter. The return value is constrained to the range [0, ].

A.1.8.3 Quat4d Class
The Quat4d class extends Tuple4d. The Quat4d is a four-element quaternion represented by double-precision floating-point x, y, z, and w values.

Constructors
public Quat4d(double x, double y, double z, double w)
public Quat4d(double q[])
public Quat4d(Quat4d q1)
public Quat4d(Quat4f q1)
public Quat4d(Tuple4d t1)
public Quat4d(Tuple4f t1)
public Quat4d()
Each of these seven constructors returns a new Quat4d. The first constructor generates a quaternion from four floating-point numbers x, y, z, and w. The second constructor generates a quaternion from the first four elements of array q of length four. The third constructor generates a quaternion from the double-precision quaternion q1. The fourth constructor generates a quaternion from the single-precision quaternion q1. The fifth and sixth constructors generate a Quat4d from tuple t1. The final constructor generates a quaternion with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void conjugate(Quat4d q1)
public final void conjugate()
The first conjugate method sets the values of this quaternion to the conjugate of quaternion q1. The second conjugate method negates the value of each of this quaternion's x, y, and z coordinates in place.
public final void mul(Quat4d q1, Quat4d q2)
public final void mul(Quat4d q1)
The first mul method sets the value of this quaternion to the quaternion product of quaternions q1 and q2 (this = q1 * q2). Note that this is safe for aliasing (that is, this can be q1 or q2). The second mul method sets the value of this quaternion to the quaternion products of itself and q1 (this = this * q1).
public final void mulInverse(Quat4d q1, Quat4d q2)
public final void mulInverse(Quat4d q1)
The first mulInverse method multiplies quaternion q1 by the inverse of quaternion q2 and places the value into this quaternion. The values of both quaternion arguments are preserved (this = q1 * q2^-1). The second mulInverse method multiplies this quaternion by the inverse of quaternion q1 and places the value into this quaternion. The value of the argument q1 is preserved (this = this * q1^-1).
public final void inverse(Quat4d q1)
public final void inverse()
The first inverse method sets the value of this quaternion to the quaternion inverse of quaternion q1. The second inverse method sets the value of this quaternion to the quaternion inverse of itself.
public final void normalize(Quat4d q1)
public final void normalize()
The first normalize method sets the value of this quaternion to the normalized value of quaternion q1. The second normalize method normalizes the value of this quaternion in place.
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
public final void set(AxisAngle4f a)
public final void set(AxisAngle4d a)
These set methods set the value of this quaternion to the rotational component of the passed matrix.
public final void interpolate(Quat4d q1, double alpha)
public final void interpolate(Quat4d q1, Quat4d q2, double  alpha)
The first method performs a great circle interpolation between this quaternion and the quaternion parameter and places the result into this quaternion. The second method performs a great circle interpolation between quaternion q1 and quaternion q2 and places the result into this quaternion.

A.1.9 Tuple4f Class
The Tuple4f class represents a four-element tuple represented by single-precision floating-point x, y, z, and w values.

Variables
The component values of a Tuple4f are directly accessible through the public variables x, y, z, and w. To access the x component of a Tuple4f called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y, z, and w components similarly.
public double x
public double y
public double z
public double w
The x, y, z, and w values, respectively.

Constructors
public Tuple4f(float x, float y, float z, float w)
public Tuple4f(float t[])
public Tuple4f(Tuple4d t1)
public Tuple4f(Tuple4f t1)
public Tuple4f()
Each of these five constructors returns a new Tuple4f. The first constructor generates a Tuple4f from four floating-point numbers x, y, z, and w. The second constructor (Tuple4f(float t[]) generates a Tuple4f from the first four elements of array t. The third constructor generates a Tuple4f from the double-precision tuple t1. The fourth constructor generates a Tuple4f from the single-precision tuple t1. The final constructor generates a Tuple4f with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(float x, float y, float z, float w)
public final void set(float t[])
public final void set(Tuple4f t1)
public final void set(Tuple4d t1)
public final void get(float t[])
public final void get(Tuple4f t)
The first set method sets the value of this tuple to the specified x, y, z, and w values. The second set method sets the value of this tuple to the specified coordinates in the array. The next two methods set the value of tuple this to the value of tuple t1. The get methods copy the value of this tuple into the tuple t.
public final void add(Tuple4f t1, Tuple4f t2)
public final void add(Tuple4f t1)
public final void sub(Tuple4f t1, Tuple4f t2)
public final void sub(Tuple4f t1)
The first add method computes the element-by-element sum of tuples t1 and t2 and places the result in this. The second add method computes the element-by-element sum of this tuple and tuple t1 and places the result in this. The first sub method performs the element-by-element subtraction of tuple t2 from tuple t1 and places the result in this (this = t1 - t2). The second sub method performs the element-by-element subtraction of tuple t1 from this tuple and places the result in this (this = this - t1).
public final void negate(Tuple4f t1)
public final void negate()
The first negate method sets the values of this tuple to the negative of the values from tuple t1. The second negate method negates the tuple this and places the resulting tuple back into this.
public final void scale(float s, Tuple4f t1)
public final void scale(float s)
public final void scaleAdd(float s, Tuple4f t1)
public final void scaleAdd(float s, Tuple4f t1, Tuple4f t2)
The first scale method multiplies each element of the tuple t1 by the scale factor s and places the resulting scaled tuple into this. The second scale method multiples the tuple this by the scale factor s, replacing this with the scaled value. The first scaleAdd method scales this tuple by the scale factor s, adds the result to tuple t1, and places the result into tuple this (this = s*this + t1). The second scaleAdd method scales the tuple t1 by the scale factor s, adds the result to the tuple t2, and places the result into the tuple this (this = s*t1 + t2).
public String toString()
This method returns a string that contains the values of this Tuple4f. The form is (x, y, z, w).
public boolean equals(Tuple4f t1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Tuple4f t1 are equal to the corresponding data members in this Tuple4f. The second method returns true if the Object t1 is of type Tuple4f and all of the data members of t1 are equal to the corresponding data members in this Tuple4f.
public boolean epsilonEquals(Tuple4f t1, float epsilon)
This method returns true if the L distance between this Tuple4f and Tuple4f t1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
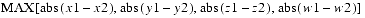public final void absolute()
public final void absolute(Tuple4f t)
The first absolute method sets each component of this tuple to its absolute value. The second absolute method sets each component of this tuple to the absolute value of the corresponding component in tuple t.
public final void clamp(float min, float max)
public final void clamp(float min, float max, Tuple4f t)
public final void clampMin(float min)
public final void clampMin(float min, Tuple4f t)
public final void clampMax(float max)
public final void clampMax(float max, Tuple4f t)
The first clamp method clamps this tuple to the range [min, max]. The second clamp method clamps this tuple to the range [min, max] and places the values into tuple t. The first clampMin method clamps the minimum value of this tuple to the min parameter. The second clampMin method clamps the minimum value of this tuple to the min parameter and places the values into the tuple t. The first clampMax method clamps the maximum value of this tuple to the max parameter. The second clampMax method clamps the maximum value of this tuple to the max parameter and places the values into the tuple t.
public void interpolate(Tuple4f t1, Tuple4f t2, float alpha)
public void interpolate(Tuple4f t1, float alpha)
The first interpolate method linearly interpolates between tuples t1 and t2 and places the result into this tuple (this = (1 - alpha) * t1 + alpha * t2). The second interpolate method linearly interpolates between this tuple and tuple t1 and places the result into this tuple (this = (1 - alpha) * this + alpha * t1).
public int hashCode()
This method returns a hash number based on the data values in this object. Two different Tuple4f objects with identical data values (that is, equals(Tuple4f) returns true) will return the same hash number. Two Tuple4f objects with different data members may return the same hash value, although this is not likely.

A.1.9.1 Point4f Class
The Point4f class extends Tuple4f. The Point4f is a four-element point represented by single-precision floating-point x, y, z, and w coordinates.

Constructors
public Point4f(float x, float y, float z, float w)
public Point4f(float p[])
public Point4f(Point4d p1)
public Point4f(Point4f p1)
public Point4f(Tuple4d t1)
public Point4f(Tuple4f t1)
public Point4f(Tuple3f t1)
public Point4f()
Each of these eight constructors returns a new Point4f. The first constructor generates a Point4f from four floating-point numbers x, y, z, and w. The second constructor (Point4f(float p[]) generates a Point4f from the first four elements of array p. The third constructor generates a Point4f from the double-precision point p1. The fourth constructor generates a Point4f from the single-precision point p1. The fifth and sixth constructors generate a Point4f from tuple t1. The seventh constructor generates a Point4f from the specified Tuple3f-the w component of this point is set to 1. The final constructor generates a Point4f with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Tuple3f t1)
This method sets the x, y, and z components of this point to the corresponding components of tuple t1. The w component of this point is set to 1.
public final float distanceSquared(Point4f p1)
public final float distance(Point4f p1)
The distanceSquared method computes the square of the Euclidean distance between this point and the point p1 and returns the result. The distance method computes the Euclidean distance between this point and the point p1 and returns the result.
public final float distanceL1(Point4f p1)
This method computes the L₁ (Manhattan) distance between this point and point p1. The L₁ distance is equal to
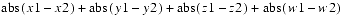public final float distanceLinf(Point4f p1)
This method computes the L distance between this point and point p1. The L distance is equal to
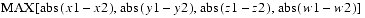public final void project(Point4f p1)
This method multiplies each of the x, y, and z components of the point p1 by , places the projected values into this point, and places a 1 into the w parameter of this point.

A.1.9.2 Color4f Class
The Color4f class extends Tuple4f. The Color4f is a four-element color value represented by single-precision floating-point x, y, z, and w values. The x, y, z, and w values represent the red, blue, green, and alpha color values, respectively. Color and alpha components should be in the range [0.0, 1.0].

Constructors
public Color4f(float x, float y, float z, float w)
public Color4f(float c[])
public Color4f(Color4f c1)
public Color4f(Tuple4d t1)
public Color4f(Tuple4f t1)
public Color4f(Color color)
public Color4f()
Each of these seven constructors returns a new Color4f. The first constructor generates a Color4f from four floating-point numbers x, y, z, and w. The second constructor generates a Color4f from the first four elements of array c. The third constructor generates a Color4f from the single-precision color c1. The fourth and fifth constructors generate a Color4f from tuple t1. The sixth constructor generates a Color4f from the specified AWT Color object. The final constructor generates a Color4f with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Color color)
public final Color get()
The set method sets the R,G,B,A values of this Color4f object to those of the specified AWT Color object. The get method returns a new AWT Color object initialized with the R,G,B,A values of this Color4f object.

A.1.9.3 Vector4f Class
The Vector4f class extends Tuple4f. The Vector4f is a four-element vector represented by single-precision floating-point x, y, z, and w coordinates.

Constructors
public Vector4f(float x, float y, float z, float w)
public Vector4f(float v[])
public Vector4f(Vector4d v1)
public Vector4f(Vector4f v1)
public Vector4f(Tuple4d t1)
public Vector4f(Tuple4f t1)
public Vector4f(Tuple3f t1)
public Vector4f()
Each of these eight constructors returns a new Vector4f. The first constructor generates a Vector4f from four floating-point numbers x, y, z, and w. The second constructor generates a Vector4f from the first four elements of array v. The third constructor generates a Vector4f from the double-precision Vector4d v1. The fourth constructor generates a Vector4f from the single-precision Vector4f v1. The fifth and sixth constructors generate a Vector4f from tuple t1. The seventh constructor generates a Vector4f from the specified Tuple3f-the w component of this vector is set to 0. The final constructor generates a Vector4f with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void set(Tuple3f t1)
This method sets the x, y, and z components of this vector to the corresponding components of tuple t1. The w component of this vector is set to 0.
public final float length()
public final float lengthSquared()
The length method computes the length of the vector this and returns its length as a single-precision floating-point number. The lengthSquared method computes the square of the length of the vector this and returns its length as a single-precision floating-point number.
public final float dot(Vector4f v1)
The dot method computes the dot product between this vector and the vector v1 and returns the resulting value.
public final void normalize(Vector4f v1)
public final void normalize()
The first normalize method sets the value of this vector to the normalization of vector v1. The second normalize method normalizes this vector in place.
public final float angle(Vector4f v1)
This method returns the (four-space) angle, in radians, between this vector and the vector v1 parameter. The return value is constrained to the range [0, ].

A.1.9.4 Quat4f Class
The Quat4f class extends Tuple4f. The Quat4f is a four-element quaternion represented by single-precision floating-point x, y, z, and w coordinates.

Constructors
public Quat4f(float x, float y, float z, float w)
public Quat4f(float q[])
public Quat4f(Quat4d q1)
public Quat4f(Quat4f q1)
public Quat4f(Tuple4d t1)
public Quat4f(Tuple4f t1)
public Quat4f()
Each of these seven constructors returns a new Quat4f. The first constructor generates a quaternion from four floating-point numbers x, y, z, and w. The second constructor generates a quaternion from the four floating-point numbers of array q of length four. The third constructor generates a quaternion from the double-precision quaternion q1. The fourth constructor generates a quaternion from the single-precision quaternion q1. The fifth and sixth constructors generate a quaternion from tuple t1. The final constructor generates a quaternion with the value of (0.0, 0.0, 0.0, 0.0).

Methods
public final void conjugate(Quat4f q1)
public final void conjugate()
The first conjugate method sets the value of this quaternion to the conjugate of quaternion q1. The second conjugate method sets the value of this quaternion to the conjugate of itself.
public final void mul(Quat4f q1, Quat4f q2)
public final void mul(Quat4f q1)
The first mul method sets the value of this quaternion to the quaternion product of quaternions q1 and q2 (this = q1 * q2). Note that this is safe for aliasing (that is, this can be q1 or q2). The second mul method sets the value of this quaternion to the quaternion product of itself and q1 (this = this * q1).
public final void mulInverse(Quat4f q1, Quat4f q2)
public final void mulInverse(Quat4f q1)
The first mulInverse method multiplies quaternion q1 by the inverse of quaternion q2 and places the value into this quaternion. The value of both argument quaternions is preserved (this = q1 * q2^-1). The second mulInverse method multiplies this quaternion by the inverse of quaternion q1 and places the value into this quaternion. The value of the argument quaternion is preserved (this = this * q1^-1).
public final void inverse(Quat4f q1)
public final void inverse()
The first inverse method sets the value of this quaternion to the quaternion inverse of quaternion q1. The second inverse method sets the value of this quaternion to the quaternion inverse of itself.
public final void normalize(Quat4f q1)
public final void normalize()
The first normalize method sets the value of this quaternion to the normalized value of quaternion q1. The second normalize method normalizes the value of this quaternion in place.
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
public final void set(AxisAngle4f a)
public final void set(AxisAngle4d a)
These set methods set the value of this quaternion to the rotational component of the passed matrix.
public final void interpolate(Quat4f q1, float alpha)
public final void interpolate(Quat4f q1, Quat4f q2, float alpha)
The first method performs a great circle interpolation between this quaternion and quaternion q1 and places the result into this quaternion. The second method performs a great circle interpolation between quaternion q1 and quaternion q2 and places the result into this quaternion.

A.1.10 Tuple4i Class
The Tuple4i class represents a four-element tuple represented by signed integer x, y, z, and w coordinates.

Variables
The component values of a Tuple4i are directly accessible through the public variables x, y, z, and w. To access the x component of a Tuple4i called upperLeftCorner, a programmer would write upperLeftCorner.x. The programmer would access the y, z, and w components similarly.
public int x
public int y
public int z
public int w
The x, y, z, and w values, respectively.

Constructors
public Tuple4i(int x, int y, int z, int w)
public Tuple4i(int[] t)
public Tuple4i(Tuple4i t1)
public Tuple4i()
Each of these four constructors returns a new Tuple4i. The first constructor generates a Tuple4i from the specified x, y, z, and w coordinates. The second constructor generates a Tuple4i from the array of length 4. The third constructor generates a Tuple4i from the specified Tuple4i. The final constructor generates a Tuple4i with the value of (0,0,0,0).

Methods
public final void set(int x, int y, int z, int w)
public final void set(int[] t)
public final void set(Tuple4i t1)
public final void get(int[] t)
public final void get(Tuple4i t)
The first set method sets the value of this tuple to the specified x, y, z, and w coordinates. The second set method sets the value of this tuple to the specified coordinates in the array of length 4. The third set method sets the value of this tuple to the value of tuple t1. The first get method copies the values of this tuple into the array t. The second get method copies the values of this tuple into the tuple t.
public final void add(Tuple4i t1, Tuple4i t2)
public final void add(Tuple4i t1)
The first method sets the value of this tuple to the sum of tuples t1 and t2. The second method sets the value of this tuple to the sum of itself and t1.
public final void sub(Tuple4i t1, Tuple4i t2)
public final void sub(Tuple4i t1)
The first method sets the value of this tuple to the difference of tuples t1 and t2 (this = t1 - t2). The second method sets the value of this tuple to the difference of itself and t1 (this = this - t1).
public final void negate(Tuple4i t1
public final void negate()
The first method sets the value of this tuple to the negation of tuple t1. The second method negates the value of this tuple in place.
public final void scale(int s, Tuple4i t1)
public final void scale(int s)
The first method sets the value of this tuple to the scalar multiplication of tuple t1. The second method sets the value of this tuple to the scalar multiplication of the scale factor with this.
public final void scaleAdd(int s, Tuple4i t1, Tuple4i t2)
public final void scaleAdd(int s, Tuple4i t1)
The first method sets the value of this tuple to the scalar multiplication of tuple t1 plus tuple t2 (this = s*t1 + t2). The second method sets the value of this tuple to the scalar multiplication of itself and then adds tuple t1 (this = s*this + t1).
public final void clamp(int min, int max, Tuple4i t)
public final void clamp(int min, int max)
The first method clamps the tuple parameter to the range [low, high] and places the values into this tuple. The second method clamps this tuple to the range [low, high].
public final void clampMin(int min, Tuple4i t)
public final void clampMin(int min)
The first method clamps the minimum value of the tuple parameter to the min parameter and places the values into this tuple. The second method clamps the minimum value of this tuple to the min parameter.
public final void clampMax(int max, Tuple4i t)
public final void clampMax(int max)
The first method clamps the maximum value of the tuple parameter to the max parameter and places the values into this tuple. The second method clamps the maximum value of this tuple to the max parameter.
public final void absolute(Tuple4i t)
public final void absolute()
The first method sets each component of the tuple parameter to its absolute value and places the modified values into this tuple. The second method sets each component of this tuple to its absolute value.
public String toString()
This method returns a string that contains the values of this Tuple4i.
public boolean equals(Object t1)
This method returns true if the Object t1 is of type Tuple4i and all of the data members of t1 are equal to the corresponding data members in this Tuple4i.
public int hashCode()
This method returns a hash code value based on the data values in this object. Two different Tuple4i objects with identical data values (that is, Tuple4i.equals returns true) will return the same hash code value. Two objects with different data members may return the same hash value, although this is not likely.

A.1.10.1 Point4i Class
The Point4i class extends Tuple4i. The Point4i is a four-element point represented by signed integer x, y, z, and w coordinates.

Constructors
public Point4i(int x, int y, int z, int w)
public Point4i(int[] t)
public Point4i(Tuple4i t1)
public Point4i()
Each of these four constructors returns a Point4i. The first constructor generates a Point4i from the specified x, y, z, and w coordinates. The second constructor generates a Point4i from the array of length 4. The third constructor generates a Point4i from the specified Tuple4i. The final constructor generates a Point4i with the value of (0,0,0,0).

A.1.11 AxisAngle4d Class
The AxisAngle4d class represents a four-element axis-angle represented by double-precision floating-point x, y, z coordinates and an angle of rotation in radians. An axis-angle is a rotation of angle radians about the vector x,y,z.

Variables
The component values of an AxisAngle4d are directly accessible through the public variables x, y, z, and angle. To access the x component of an AxisAngle4d called myRotation, a programmer would write myRotation.x. The programmer would access the y, z, and angle components similarly.
public double x
public double y
public double z
public double angle
The x, y, and z coordinates and the rotational angle, respectively. The rotation angle is expressed in radians.

Constructors
public AxisAngle4d(double x, double y, double z, double angle)
public AxisAngle4d(double a[])
public AxisAngle4d(AxisAngle4d a1)
public AxisAngle4d(AxisAngle4f a1)
public AxisAngle4d(Vector3d axis, double angle)
public AxisAngle4d()
Each of these six constructors returns a new AxisAngle4d. The first constructor generates an axis-angle from four floating-point numbers x, y, z, and angle. The second constructor generates an axis-angle from the first four elements of array a. The third constructor generates an axis-angle from the double-precision axis-angle a1. The fourth constructor generates an axis-angle from the single-precision axis-angle a1. The fifth constructor generates an axis-angle from the specified axis and angle. The final constructor generates an axis-angle with the value of (0.0, 0.0, 1.0, 0.0).

Methods
public final void set(double x, double y, double z, double  angle)
public final void set(double a[])
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
public final void set(AxisAngle4f a1)
public final void set(AxisAngle4d a1)
public final void set(Quat4f q1)
public final void set(Quat4d q1)
public final void set(Vector3d axis, double angle)
public final void get(double a[])
The first set method sets the value of this axis-angle to the specified x, y, z, and angle coordinates. The second set method sets the value of this axis-angle to the specified x,y,z angle. The next four set methods set the value of this axis-angle to the rotational component of the passed matrix m1. The next two set methods set the value of this axis-angle to the value of axis-angle a1. The next two set methods set the value of this axis-angle to the value of the passed quaternion q1. The last set method sets the value of this axis-angle to the specified axis and angle. The get method retrieves the value of this axis-angle and places it into the array a of length four in x,y,z,angle order.
public String toString()
This method returns a string that contains the values of this AxisAngle4d. The form is (x, y, z, angle).
public boolean equals(AxisAngle4d v1)
public boolean equals(Object o1)
The first method returns true if all of the data members of AxisAngle4d v1 are equal to the corresponding data members in this axis-angle. The second method returns true if the Object o1 is of type AxisAngle4d and all of the data members of o1 are equal to the corresponding data members in this AxisAngle4d.
public boolean epsilonEquals(AxisAngle4d a1, double epsilon)
This method returns true if the L distance between this axis-angle and axis-angle a1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
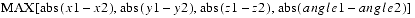public int hashCode()
This method returns a hash number based on the data values in this object. Two different AxisAngle4d objects with identical data values (that is, equals(AxisAngle4d) returns true) will return the same hash number. Two AxisAngle4d objects with different data members may return the same hash value, although this is not likely.

A.1.12 AxisAngle4f Class
The AxisAngle4f class represents a four-element axis-angle represented by single-precision floating-point x, y, and z coordinates and an angle of rotation in radians. An axis-angle is a rotation of angle radians about the vector x,y,z.

Variables
The component values of an AxisAngle4f are directly accessible through the public variables x, y, z, and angle. To access the x component of an AxisAngle4f called myRotation, a programmer would write myRotation.x. The programmer would access the y, z, and angle components similarly.
public float x
public float y
public float z
public float angle
The x, y, and z coordinates and the rotational angle, respectively. The rotation angle is expressed in radians.

Constructors
public AxisAngle4f(float x, float y, float z, float angle)
public AxisAngle4f(float a[])
public AxisAngle4f(AxisAngle4f a1)
public AxisAngle4f(AxisAngle4d a1)
public AxisAngle4f(Vector3f axis, float angle)
public AxisAngle4f()
Each of these six constructors returns a new AxisAngle4f. The first constructor generates an axis-angle from four floating-point numbers x, y, z, and angle. The second constructor generates an axis-angle from the first four elements of array a. The third constructor generates an axis-angle from the single-precision axis-angle a1. The fourth constructor generates an axis-angle from the double-precision axis-angle a1. The fifth constructor generates an axis-angle from the specified axis and angle. The final constructor generates an axis-angle with the value of (0.0, 0.0, 1.0, 0.0).

Methods
public final void set(float x, float y, float z, float angle)
public final void set(float a[])
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
public final void set(AxisAngle4f a1)
public final void set(AxisAngle4d a1)
public final void set(Quat4f q1)
public final void set(Quat4d q1)
public final void set(Vector3f axis, float angle)
public final void get(float a[])
The first set method sets the value of this axis-angle to the specified x, y, z, and angle coordinates. The second set method sets the value of this axis-angle to the specified coordinates in the array a. The next four set methods set the value of this axis-angle to the rotational component of the passed matrix m1. The next two set methods set the value of this axis-angle to the value of axis-angle a1. The next two set methods set the value of this axis-angle to the value of the passed quaternion q1. The last set method sets the value of this axis-angle to the specified axis and angle. The get method retrieves the value of this axis-angle and places it into the array a of length four in x,y,z,angle order.
public String toString()
This method returns a string that contains the values of this axis-angle. The form is (x, y, z, angle).
public boolean equals(AxisAngle4f a1)
public boolean equals(Object o1)
The first method returns true if all of the data members of axis-angle a1 are equal to the corresponding data members in this axis-angle. The second method returns true if the Object o1 is of type AxisAngle4f and all of the data members of o1 are equal to the corresponding data members in this AxisAngle4f.
public boolean epsilonEquals(AxisAngle4f a1, float epsilon)
This method returns true if the L distance between this axis-angle and axis-angle a1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
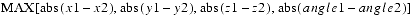public int hashCode()
This method returns a hash number based on the data values in this object. Two different AxisAngle4f objects with identical data values (that is, equals(AxisAngle4f) returns true) will return the same hash number. Two AxisAngle4f objects with different data members may return the same hash value, although this is not likely.

A.1.13 GVector Class
The GVector class represents a double-precision, general, dynamically resizable, one-dimensional vector class. Index numbering begins with zero.

Constructors
public GVector(int length)
public GVector(double vector[])
public GVector(GVector vector)
public GVector(Tuple2f tuple)
public GVector(Tuple3f tuple)
public GVector(Tuple3d tuple)
public GVector(Tuple4f tuple)
public GVector(Tuple4d tuple)
public GVector(double vector[], int length)
Each of these nine constructors returns a new GVector. The first constructor generates a generalized mathematical vector with all elements set to 0.0: length represents the number of elements in the vector. The second and third constructors generate a generalized mathematical vector and copy the initial value from the parameter vector. The next four constructors generate a generalized mathematical vector and copy the initial value from the tuple parameter tuple. The final method generates a generalized mathematical vector by copying length elements from the array parameter. The array must contain at least length elements (that is, vector.length length). The length of this new GVector is set to the specified length.

Methods
public final void add(GVector v1)
public final void add(GVector v1, GVector v2)
public final void sub(GVector v1)
public final void sub(GVector v1, GVector v2)
The first add method computes the element-by-element sum of this GVector and GVector v1 and places the result in this. The second add method computes the element-by-element sum of GVectors v1 and v2 and places the result in this. The first sub method performs the element-by-element subtraction of GVector v1 from this GVector and places the result in this (this = this - v1). The second sub method performs the element-by-element subtraction of GVector v2 from GVector v1 and places the result in this (this = v1 - v2).
public final void mul(GMatrix m1, GVector v1)
public final void mul(GVector v1, GMatrix m1)
The first mul method multiplies matrix m1 times vector v1 and places the result into this vector (this = m1 * v1). The second mul method multiplies the transpose of vector v1 (that is, v1 becomes a row vector with respect to the multiplication) times matrix m1 and places the result into this vector (this = transpose(v1) * m1). The result is technically a row vector, but the GVector class knows only about column vectors, so the result is stored as a column vector.
public final void negate()
This method negates the vector this and places the resulting vector back into this.
public final void zero()
This method sets all the values in this vector to zero.
public final void setSize(int length)
public final void int getSize()
This method changes the size of this vector dynamically. If the size is increased, no data values are lost. If the size is decreased, only those data values whose vector positions were eliminated are lost.
public final void set(double v[])
public final void set(GVector v)
public final void set(Tuple2f t)
public final void set(Tuple3f t)
public final void set(Tuple3d t)
public final void set(Tuple4f t)
public final void set(Tuple4d t)
The first set method sets the values of this vector to the values found in the array v: The array should at least be equal in length to the number of elements in the vector. The second set method sets the values of this vector to the values in vector v. The last 5 set methods set the value of this vector to the values in tuple t.
public final double getElement(int index)
public final void setElement(int index, double value)
These methods set and retrieve the specified index value of this vector.
public final double norm()
public final double normSquared()
The norm method returns the square root of the sum of the squares of this vector (its length in n-dimensional space). The normSquared method returns the sum of the squares of this vector (its length in n-dimensional space).
public final void normalize(GVector v1)
public final void normalize()
The first normalize method sets the value of this vector to the normalization of vector v1. The second normalize method normalizes this vector in place.
public final void scale(double s, GVector v1)
public final void scale(double s)
public final void scaleAdd(double s, GVector v1, GVector v2)
The first scale method sets the value of this vector to the scalar multiplication of the scale factor s with the vector v1. The second scale method scales this vector by the scale factor s. The scaleAdd method scales the vector v1 by the scale factor s, adds the result to the vector v2, and places the result into this vector (this = s*v1 + v2).
public String toString()
This method returns a string that contains the values of this vector.
public int hashCode()
This method returns a hash number based on the data values in this object. Two different GVector objects with identical data values (that is, equals(GVector) returns true) will return the same hash number. Two objects with different data members may return the same hash value, although this is not likely.
public boolean equals(GVector vector1)
public boolean equals(Object o1)
The first method returns true if all of the data members of GVector vector1 are equal to the corresponding data members in this GVector. The second method returns true if the Object o1 is of type GMatrix and all of the data members of o1 are equal to the corresponding data members in this GMatrix.
public boolean epsilonEquals(GVector v1, double epsilon)
This method returns true if the L distance between this vector and vector v1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to
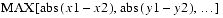public final double dot(GVector v1)
This method returns the dot product of this vector and vector v1.
public final void SVDBackSolve(GMatrix U, GMatrix W, GMatrix V,
       GVector x)
public final void LUDBackSolve(GMatrix LU, GVector b,
       GVector  permutation)
The first method solves for x in Ax = b, where x is this vector (n x 1), b is an m x 1 vector, and A is an m x n matrix, defined as A = U * W * transpose(V). U, W, and V must be precomputed and can be found by taking the singular value decomposition (SVD) of A. The second method takes the LU matrix and the permutation vector produced by the GMatrix method LUD and solves the equation LU * x = b by placing the solution to the set of linear equations into this vector (x).
public final double angle(GVector v1)
This method returns the (n-space) angle, in radians, between this vector and the vector v1 parameter. The return value is constrained to the range [0, ].
public final void interpolate(GVector v1, GVector v2, float  alpha)
public final void interpolate(GVector v1, float alpha)
Deprecated methods. See the following two methods.
public final void interpolate(GVector v1, GVector v2, double  alpha)
public final void interpolate(GVector v1, double alpha)
The first method linearly interpolates between vectors v1 and v2 and places the result into this vector (this = (1 - alpha) * v1 + alpha * v2). The second method linearly interpolates between this vector and vector v1 and places the result into this vector (this = (1 - alpha) * this + alpha * v1).

A.2 Matrix Objects
Java 3D uses matrix objects to represent rotations and full 3D transformations. The matrix classes (as well as the associated Tuple and AxisAngle classes) include code for accessing, manipulating, and updating the matrix, vector, and AxisAngle classes. Java 3D further subdivides the matrix classes into 3 x 3 matrices (mainly to store rotations) and 4 x 4 matrices (mainly to store more complex 3D transformations). These two classes in turn provide support for both single-precision floating-point representations and double-precision floating-point representations.
Matrix operations try to minimize gratuitous allocation of memory; thus all matrix operations update an existing object. To multiply two matrices together and store the result in a third, a Java 3D application or applet would write matrix3.mul(matrix1, matrix2). Here matrix3 receives the results of multiplying matrix1 with matrix2.
The Java 3D model for 3 x 3 transformations is

The Java 3D model for 4 x 4 transformations is

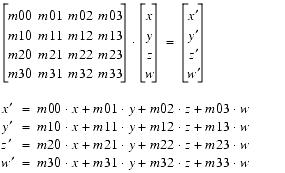
Note: When transforming a Point3f or a Point3d, the input w is set to 1. When transforming a Vector3f or Vector3d, the input w is set to 0.

A.2.1 Matrix3f Class
The Matrix3f class serves to contain 3 x 3 matrices mainly for storing and manipulating 3D rotation matrices. The class includes five different constructors for creating matrices and several operators for manipulating these matrices.

Variables
The component values of a Matrix3f are directly accessible through the public variables m00, m01, m02, m10, m11, m12, m20, m21, and m22. To access the element in row 2 and column 0 of matrix rotate, a programmer would write rotate.m20. A programmer would access the other values similarly.
public float m00
public float m01
public float m02
public float m10
public float m11
public float m12
public float m20
public float m21
public float m22
These public variables are the elements of the matrix.

Constructors
public Matrix3f(float m00, float m01, float m02, float m10,
       float  m11, float m12, float m20, float m21, float m22)
public Matrix3f(float v[])
public Matrix3f(Matrix3d m1)
public Matrix3f(Matrix3f m1)
public Matrix3f()
Each of these constructors returns a new Matrix3f object. The first constructor generates a 3 x 3 matrix from the nine values provided. The second constructor generates a 3 x 3 matrix from the first nine values in the array v. The third and fourth constructors generate a new matrix with the same values as the passed matrix m1. The final constructor generates a 3 x 3 matrix with all nine values set to 0.0.

Methods
public final void set(Quat4d q1)
public final void set(Quat4f q1)
These two set methods set the value of the matrix this to the matrix conversion of the quaternion argument q1.
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
Sets the value of this matrix to the value of the argument.
public final void set(AxisAngle4d a1)
public final void set(AxisAngle4f a1)
These two set methods set the value of the matrix this to the matrix conversion of the axis and angle argument a1.
public final void set(float scale)
public final void set(float m[])
The first method sets the value of this matrix to a scale matrix with the passed scale amount. The second method sets the values of this matrix to the row-major array parameter (that is, the first three elements of the array are copied into the first row of this matrix, and so forth).
public final void setElement(int row, int column, float value)
public final float getElement(int row, int column)
The setElement and getElement methods provide a means for accessing a single element within a 3 x 3 matrix using indices. This is not a preferred method of access, but Java 3D provides these methods for functional completeness. The setElement method takes a row index row (where a value of 0 represents the first row and a value of 2 represents the third row), a column index column (where a value of 0 represents the first column and a value of 2 represents the third column), and a value. It sets the corresponding element in matrix this to the specified value. The getElement method also takes a row index row and a column index column. It returns the element at the corresponding locations as a floating-point value.
public final void setRow(int row, float x, float y, float z)
public final void setRow(int row, Vector3f v)
public final void setRow(int row, float v[])
public final void getRow(int row, Vector3f v)
public final void getRow(int row, float v[])
The three setRow methods provide a means for constructing a 3 x 3 matrix on a row basis. The row parameter row determines which row the method invocation affects. A row value of 0 represents the first row and a value of 2 represents the third row. The first setRow method specifies the three new values as independent floating-point values. The second setRow method uses the values in the Vector3f v to update the matrix. The third setRow method uses the first three values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getRow methods copy the matrix values in the specified row into the vector or array parameter, respectively.
public final void setColumn(int column, float x, float y, float  z)
public final void setColumn(int column, Vector3f v)
public final void setColumn(int column, float v[])
public final void getColumn(int column, Vector3f v)
public final void getColumn(int column, float v[])
The three setColumn methods provide a means for constructing a 3 x 3 matrix on a column basis. The column parameter determines which column the method invocation affects. A column value of 0 represents the first column and a value of 2 represents the third column. The first setColumn method specifies the three new values as independent floating-point values. The second setColumn method uses the values in the Vector3f v to update the matrix. The third setColumn method uses the first three values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getColumn methods copy the matrix values in the specified column into the vector or array parameter, respectively.
public final void setZero()
This method sets this matrix to all zeros.
public final void setIdentity()
This method sets this Matrix3f to identity.
public final void add(Matrix3f m1, Matrix3f m2)
public final void add(Matrix3f m1)
public final void sub(Matrix3f m1, Matrix3f m2)
public final void sub(Matrix3f m1)
The first add method adds the matrix m1 to the matrix m2 and places the result into the matrix this. The second add method adds the matrix this to the matrix m1 and places the result into the matrix this. The first sub method performs an element-by-element subtraction of matrix m2 from matrix m1 and places the result into the matrix this. The second sub method performs an element-by-element subtraction of the matrix m1 from the matrix this and places the result into the matrix this.
public final void transform(Tuple3f t)
public final void transform(Tuple3f t, Tuple3f result)
The first method multiplies this matrix by the tuple t and places the result back into the tuple (t = this*t). The second method multiplies this matrix by the tuple t and places the result into the tuple result (result = this*t).
public final void transpose()
public final void transpose(Matrix3f m1)
The first method transposes this matrix in place. The second method sets the value of this matrix to the transpose of the matrix m1.
public final void invert()
public final void invert(Matrix3f m1)
The first method inverts this matrix in place. The second method sets the value of this matrix to the inverse of the matrix m1.
public final float determinant()
The determinant method computes the determinant of the matrix this and returns the computed value.
public final void rotX(float angle)
public final void rotY(float angle)
public final void rotZ(float angle)
The three rot methods construct rotation matrices that rotate in a counterclockwise (right-handed) direction around the axis specified as the last letter of the method name. The constructed matrix replaces the value of the matrix this. The rotation angle is expressed in radians.
public final void mul(Matrix3f m1, Matrix3f m2)
public final void mul(Matrix3f m1)
The first mul method multiplies matrix m1 with matrix m2 and places the result into the matrix this. The second mul method multiplies the matrix this with the matrix m1 and places the result into matrix this.
public final void mulNormalize(Matrix3f m1)
public final void mulNormalize(Matrix3f m1, Matrix3f m2)
The first mulNormalize method multiplies this matrix by matrix m1, performs an SVD normalization of the result, and places the result back into this matrix (this = SVDnorm(this · m1)). The second mulNormalize method multiplies matrix m1 by matrix m2, performs an SVD normalization of the result, and places the result into this matrix (this = SVDnorm(m1 · m2)).
public final void mulTransposeBoth(Matrix3f m1, Matrix3f m2)
public final void mulTransposeRight(Matrix3f m1, Matrix3f m2)
public final void mulTransposeLeft(Matrix3f m1, Matrix3f m2)
The mulTransposeBoth method multiplies the transpose of matrix m1 (left) times the transpose of matrix m2 (right) and places the result into this matrix. The mulTransposeRight method multiplies matrix m1 times the transpose of matrix m2 and places the result back into this matrix. The mulTransposeLeft method multiplies the transpose of matrix m1 times matrix m2 and places the result into this matrix.
public final void normalize()
public final void normalize(Matrix3f m1)
The first normalize method performs a singular value decomposition normalization of this matrix. The second normalize method performs a singular value decomposition normalization of matrix m1 and places the normalized values into this.
public final void normalizeCP()
public final void normalizeCP(Matrix3f m1)
The first normalizeCP method performs a cross-product normalization of this matrix. The second normalizeCP method performs a cross-product normalization of matrix m1 and places the normalized values into this.
public boolean equals(Matrix3f m1)
public boolean equals(Object o1)
The first method returns true if all of the data members of Matrix3f m1 are equal to the corresponding data members in this Matrix3f. The second method returns true if the Object o1 is of type Matrix3f and all of the data members of o1 are equal to the corresponding data members in this Matrix3f.
public boolean epsilonEquals(Matrix3f m1, float epsilon)
This method returns true if the L distance between this Matrix3f and Matrix3f m1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to

MAX[i = 0,1,2, ... n; j = 0,1,2,... n; abs(this.m(i,j) - m1.m(i,j)]
public final void negate()
public final void negate(Matrix3f m1)
The first method negates the value of this matrix in place (this = -this). The second method sets the value of this matrix equal to the negation of the matrix m1 (this = -m1).
public final float getScale()
This method performs an SVD normalization of this matrix to calculate and return the uniform scale factor. If the matrix has nonuniform scale factors, the largest of the x, y, and z scale factors will be returned.
public final void setScale(float scale)
This method sets the scale component of the current matrix by factoring out the current scale (by doing an SVD) and multiplying by the new scale.
public final void add(float scalar)
This method adds a scalar to each component of this matrix.
public final void add(float scalar, Matrix3f m1)
This method adds a scalar to each component of the matrix m1 and places the result into this. Matrix m1 is not modified.
public final void mul(float scalar, Matrix3f m1)
This method multiplies each component of the matrix m1 by a scalar and places the result into this. Matrix m1 is not modified.
public final void mul(float scalar)
This method multiplies each element of this matrix by a scalar.
public final void transform(Tuple3f t)
public final void transform(Tuple3f t, Tuple3f result)
The first method multiplies this matrix by the tuple t and places the result back into the tuple (t = this*t). The second method multiplies this matrix by the tuple t and places the result into the tuple result (result = this*t).
public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two different Matrix3f objects with identical data values (that is, equals(Matrix3f) returns true) will return the same hash number. Two Matrix3f objects with different data members may return the same hash value, although this is not likely.
public String toString()
The toString method returns a string that contains the values of this Matrix3f.

A.2.2 Matrix3d Class
The Matrix3d class serves to contain 3 x 3 matrices mainly for storing and manipulating 3D rotation matrices. The class includes five different constructors for creating matrices and several operators for manipulating these matrices.

Variables
The component values of a Matrix3d are directly accessible through the public variables m00, m01, m02, m10, m11, m12, m20, m21, and m22. To access the element in row 2 and column 0 of the matrix named rotate, a programmer would write rotate.m20. Other matrix values are accessed similarly.
public double m00
public double m01
public double m02
public double m10
public double m11
public double m12
public double m20
public double m21
public double m22
These public variables are the elements of the matrix.

Constructors
public Matrix3d(double m00, double m01, double m02, double m10,
       double m11, double m12, double m20, double  m21, double  m22)
public Matrix3d(double v[])
public Matrix3d()
public Matrix3d(Matrix3d m1)
public Matrix3d(Matrix3f m1)
Each of these constructors returns a new Matrix3d object. The first constructor generates a 3 x 3 matrix from the nine values provided. The second constructor generates a 3 x 3 matrix from the first nine values in the array v. The third constructor generates a 3 x 3 matrix with all nine values set to 0.0. The fourth and fifth constructors generate a 3 x 3 matrix with the same values as the matrix m1 parameter.

Methods
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
These methods set the value of this matrix to the value of the argument.
public final void set(double scale)
public final void set(double m[])
These methods set the value of the matrix this to a scale matrix with the passed scale amount.
public final void set(AxisAngle4d a1)
public final void set(AxisAngle4f a1)
These two set methods set the value of the matrix this to the matrix conversion of the axis and angle argument a1.
public final void set(Quat4d q1)
public final void set(Quat4f q1)
These two set methods set the value of the matrix this to the matrix conversion of the quaternion argument q1.
public final void setElement(int row, int column, double value)
public final double getElement(int row, int column)
The setElement and getElement methods provide a means for accessing a single element within a 3 x 3 matrix using indices. This is not a preferred method of access, but Java 3D provides these methods for functional completeness. The setElement method takes a row index row (where a value of 0 represents the first row and a value of 2 represents the third row), a column index column (where a value of 0 represents the first column and a value of 2 represents the third column), and a value. It sets the corresponding element in matrix this to the specified value. The getElement method also takes a row index row and a column index column and returns the element at the corresponding locations as a floating-point value.
public final void setRow(int row, double x, double y, double z)
public final void setRow(int row, Vector3d v)
public final void setRow(int row, double v[])
public final void getRow(int row, Vector3d v)
public final void getRow(int row, double v[])
The three setRow methods provide a means for constructing a 3 x 3 matrix on a row basis. The row parameter determines which row the method invocation affects. A row value of 0 represents the first row, and a value of 2 represents the third row. The first setRow method specifies the three new values as independent floating-point values. The second setRow method uses the values in the Vector3d v to update the matrix. The third setRow method uses the first three values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getRow methods copy the matrix values in the specified row into the array or vector parameter, respectively.
public final void setColumn(int column, double x, double y,
       double  z)
public final void setColumn(int column, Vector3d v)
public final void setColumn(int column, double v[])
public final void getColumn(int column, Vector3d v)
public final void getColumn(int column, double v[])
The three setColumn methods provide a means for constructing a 3 x 3 matrix on a column basis. The column parameter determines which column the method invocation affects. A column value of 0 represents the first column, and a value of 2 represents the third column. The first setColumn method specifies the three new values as independent floating-point values. The second setColumn method uses the values in the Vector3d v to update the matrix. The third setColumn method uses the first three values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getColumn methods copy the matrix values in the specified column into the array or vector parameter, respectively.
public final void add(Matrix3d m1, Matrix3d m2)
public final void add(Matrix3d m1)
public final void sub(Matrix3d m1, Matrix3d m2)
public final void sub(Matrix3d m1)
The first add method adds the matrix m1 to the matrix m2 and places the result into the matrix this. The second add method adds the matrix this to the matrix m1 and places the result into the matrix this. The first sub method performs an element-by-element subtraction of matrix m2 from matrix m1 and places the result into the matrix this. The second sub method performs an element-by-element subtraction of the matrix m1 from the matrix this and places the result into the matrix this.
public final void add(double scalar)
This method adds a scalar to each component of this matrix.
public final void add(double scalar, Matrix3d m1)
This method adds a scalar to each component of the matrix m1 and places the result into this. Matrix m1 is not modified.
public final void transform(Tuple3d t)
public final void transform(Tuple3d t, Tuple3d result)
The first method multiplies this matrix by the tuple t and places the result back into the tuple (t = this*t). The second method multiplies this matrix by the tuple t and places the result into the tuple result (result = this*t).
public final void transpose()
public final void transpose(Matrix3d m1)
The first method transposes this matrix in place. The second method sets the value of this matrix to the transpose of the matrix m1.
public final void invert()
public final void invert(Matrix3d m1)
The first method inverts this matrix in place. The second method sets the value of this matrix to the inverse of the matrix m1.
public final double determinant()
The determinant method computes the determinant of the matrix this and returns the computed value.
public final void rotX(double angle)
public final void rotY(double angle)
public final void rotZ(double angle)
The three rot methods construct rotation matrices that rotate in a counterclockwise (right-handed) direction around the axis specified by the final letter of the method name. The constructed matrix replaces the value of the matrix this. The rotation angle is expressed in radians.
public final void mul(Matrix3d m1, Matrix3d m2)
public final void mul(Matrix3d m1)
The first mul method multiplies matrix m1 with matrix m2 and places the result into the matrix this. The second mul method multiplies matrix this with matrix m1 and places the result into the matrix this.
public final void mulNormalize(Matrix3d m1)
public final void mulNormalize(Matrix3d m1, Matrix3d m2)
The first mulNormalize method multiplies this matrix by matrix m1, performs an SVD normalization of the result, and places the result back into this matrix (this = SVDnorm(this · m1)). The second mulNormalize method multiplies matrix m1 by matrix m2, performs an SVD normalization of the result, and places the result into this matrix (this = SVDnorm(m1 · m2)).
public final void mulTransposeBoth(Matrix3d m1, Matrix3d m2)
public final void mulTransposeRight(Matrix3d m1, Matrix3d m2)
public final void mulTransposeLeft(Matrix3d m1, Matrix3d m2)
The mulTransposeBoth method multiplies the transpose of matrix m1 (left) times the transpose of matrix m2 (right) and places the result into this matrix. The mulTransposeRight method multiplies matrix m1 times the transpose of matrix m2 and places the result back into this matrix. The mulTransposeLeft method multiplies the transpose of matrix m1 times matrix m2 and places the result into this matrix.
public final void normalize()
public final void normalize(Matrix3d m1)
The first normalize method performs a singular value decomposition normalization of this matrix. The second normalize method performs a singular value decomposition normalization of matrix m1 and places the normalized values into this.
public final void normalizeCP()
public final void normalizeCP(Matrix3d m1)
The first normalizeCP method performs a cross-product normalization of this matrix. The second normalizeCP method performs a cross-product normalization of matrix m1 and places the normalized values into this.
public boolean equals(Matrix3d m1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Matrix3d m1 are equal to the corresponding data members in this Matrix3d. The second method returns true if the Object t1 is of type Matrix3d and all of the data members of t1 are equal to the corresponding data members in this Matrix3d.
public boolean epsilonEquals(Matrix3d m1, double epsilon)
This method returns true if the L distance between this Matrix3d and Matrix3d m1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to

MAX[i = 0,1,2,; j = 0,1,2,; abs(this.m(i,j) - m1.m(i,j)]
public final void negate()
public final void negate(Matrix3d m1)
The first method negates the value of this matrix in place (this = -this). The second method sets the value of this matrix equal to the negation of the matrix m1 (this = -m1).
public final double getScale()
This method performs an SVD normalization of this matrix to calculate and return the uniform scale factor. If the matrix has non-uniform scale factors, the largest of the x, y, and z scale factors will be returned.
public final void setScale(double scale)
This method sets the scale component of the current matrix by factoring out the current scale (by doing an SVD) and multiplying by the new scale.
public final void mul(double scalar, Matrix3d m1)
This method multiplies each component of the matrix m1 by a scalar and places the result into this. Matrix m1 is not modified.
public final void mul(double scalar)
This method multiplies each element of this matrix by a scalar.
public final void transform(Tuple3d t)
public final void transform(Tuple3d t, Tuple3d result)
The first method multiplies this matrix by the tuple t and places the result back into the tuple (t = this*t). The second method multiplies this matrix by the tuple t and places the result into the tuple result (result = this*t).
public final void setZero()
This method sets this matrix to all zeros.
public final void setIdentity()
This method sets this Matrix3d to identity.
public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two different Matrix3d objects with identical data values (that is, equals(Matrix3d) returns true) will return the same hash number. Two Matrix3d objects with different data members may return the same hash value, although this is not likely.
public String toString()
The toString method returns a string that contains the values of this Matrix3d.

A.2.3 Matrix4f Class
The Matrix4f class serves to contain 4 x 4 matrices mainly for storing and manipulating 3D transformation matrices. The class includes seven different constructors for creating matrices and several operators for manipulating these matrices.

Variables
The component values of a Matrix4f are directly accessible through the public variables m00, m01, m02, m03, m10, m11, m12, m13, m20, m21, m22, m23, m30, m31, m32, and m33. To access the element in row 2 and column 0 of matrix rotate, a programmer would write rotate.m20. A programmer would access the other values similarly.
public float m00
public float m01
public float m02
public float m03
public float m10
public float m11
public float m12
public float m13
public float m20
public float m21
public float m22
public float m23
public float m30
public float m31
public float m32
public float m33
These public variables are the elements of the matrix.

Constructors
public Matrix4f(float m00, float m01, float m02, float m03,
       float m10, float m11, float m12, float m13,
       float m20, float  m21, float m22, float m23, float m30,
       float m31, float  m32, float  m33)
public Matrix4f(float v[])
public Matrix4f(Quat4f q1, Vector3f t1, float s)
public Matrix4f(Matrix4d m1)
public Matrix4f(Matrix4f m1)
public Matrix4f(Matrix3f m1, Vector3f t1, float s)
public Matrix4f()
Each of these constructors returns a new Matrix4f object. The first constructor generates a 4 x 4 matrix from the 16 values provided. The second constructor generates a 4 x 4 matrix from the first 16 values in the array v. The third constructor generates a 4 x 4 matrix from the quaternion, translation, and scale values. The scale is applied only to the rotational components of the matrix (upper 3 x 3) and not to the translational components. The fourth and fifth constructors generate a 4 x 4 matrix with the same values as the passed matrix m1. The sixth constructor generates a 4 x 4 matrix from the rotation matrix, translation, and scale values. The scale is applied only to the rotational components of the matrix (upper 3 x 3) and not to the translational components of the matrix. The final constructor generates a 4 x 4 matrix with all 16 values set to 0.0.

Methods
public final void set(Quat4f q1)
public final void set(Quat4d q1)
public final void set(Quat4f q1, Vector3f t1, float s)
public final void set(Quat4d q1, Vector3d t1, double s)
public final void set(Matrix4d m1)
public final void set(Matrix4f m1)
public final void set(AxisAngle4f a1)
public final void set(AxisAngle4d a1)
The first two set methods set the value of this matrix to the matrix conversion of the quaternion argument q1. The next two set methods set the value of this matrix from the rotation expressed by the quaternion q1, the translation t1, and the scale s. The next two set methods set the value of this matrix to a copy of the passed matrix m1. The last two set methods set the value of this matrix to the matrix conversion of the axis and angle argument a1.
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
These methods set the rotational component (upper 3 x 3) of this matrix to the matrix values in the m1 argument. The other elements of this matrix are initialized as if this were an identity matrix (that is, an affine matrix with no translational component).
public final void set(float scale)
public final void set(float m[])
The first method sets the value of this matrix to a scale matrix with the passed scale amount. The second method sets the value of this matrix to the row-major array parameter (that is, the first four elements of the array are copied into the first row of this matrix, and so forth).
public final void set(Vector3f v1)
This method sets the value of this matrix to a translation matrix with the passed translation value.
public final void set(float scale, Vector3f t1)
public final void set(Vector3f t1, float scale)
These methods set the value of this matrix to a scale and translation matrix. In the first method, the scale is not applied to the translation, and all of the matrix values are modified. In the second method, the translation is scaled by the scale factor, and all of the matrix values are modified.
public final void set(Matrix3f m1, Vector3f t1, float scale)
public final void set(Matrix3d m1, Vector3d t1, double scale)
These two methods set the value of this matrix from the rotation expressed by the rotation matrix m1, the translation t1, and the scale scale. The translation is not modified by the scale.
public final void get(Matrix3d m1)
public final void get(Matrix3f m1)
public final float get(Matrix3f m1, Vector3f t1)
public final void get(Quat4f q1)
public final void get(Vector3f trans)
The first two methods perform an SVD normalization of this matrix in order to acquire the normalized rotational component. The values are placed into the matrix parameter m1. The third method performs an SVD normalization of this matrix to calculate the rotation as a 3 x 3 matrix, the translation, and the scale. None of the matrix values in this matrix is modified. The fourth method performs an SVD normalization of this matrix to acquire the normalized rotational component. The values are placed into the quaternion q1. The final method retrieves the translational components of this matrix and copies them into the vector trans.
public final void setElement(int row, int column, float value)
public final float getElement(int row, int column)
The setElement and getElement methods provide a means for accessing a single element within a 4 x 4 matrix using indices. This is not a preferred method of access, but Java 3D provides these methods for functional completeness. The setElement method takes a row index row (where a value of 0 represents the first row and a value of 3 represents the fourth row), a column index column (where a value of 0 represents the first column and a value of 3 represents the fourth column), and a value. It sets the corresponding element in matrix this to the specified value. The getElement method also takes a row index row and a column index column and returns the element at the corresponding locations as a floating-point value.
public final void getRotationScale(Matrix3f m1)
This method retrieves the upper 3 x 3 values of this matrix and places them into the matrix m1.
public final void setScale(float scale)
public final float getScale()
The first method sets the scale component of the current matrix by factoring out the current scale (by doing an SVD) and multiplying by the new scale. The second method performs an SVD normalization of this matrix to calculate and return the uniform scale factor. If the matrix has nonuniform scale factors, the largest of the x, y, and z scale factors will be returned.
public final void add(float scalar)
This method adds a scalar to each component of this matrix.
public final void add(float scalar, Matrix4f m1)
This method adds a scalar to each component of the matrix m1 and places the result into this. Matrix m1 is not modified.
public final void mul(float scalar, Matrix4f m1)
This method multiplies each component of the matrix m1 by a scalar and places the result into this. Matrix m1 is not modified.
public final void mul(float scalar)
This method multiplies each element of this matrix by a scalar.
public final void setRow(int row, float x, float y, float z,
       float  w)
public final void setRow(int row, Vector4f v)
public final void setRow(int row, float v[])
public final void getRow(int row, Vector4f v)
public final void getRow(int row, float v[])
The three setRow methods provide a means for constructing a 4 x 4 matrix on a row basis. The row parameter row determines which row the method invocation affects. A row value of 0 represents the first row, and a value of 3 represents the fourth row. The first setRow method specifies the four new values as independent floating-point values. The second setRow method uses the values in the Vector4f v to update the matrix. The third setRow method uses the first four values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getRow methods copy the matrix values in the specified row into the array or vector parameter, respectively.
public final void setColumn(int column, float x, float y, float  z,
       float  w)
public final void setColumn(int column, Vector4f v)
public final void setColumn(int column, float v[])
public final void getColumn(int column, Vector4f v)
public final void getColumn(int column, float v[])
The three setColumn methods provide a means for constructing a 4 x 4 matrix on a column basis. The column parameter determines which column the method invocation affects. A column value of 0 represents the first column, and a value of 3 represents the fourth column. The first setColumn method specifies the four new values as independent double-precision floating-point values. The second setColumn method uses the values in the Vector4f v to update the matrix. The third setColumn method uses the first four values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getColumn methods copy the matrix values in the specified column into the array or vector parameter, respectively.
public final void setRotation(Matrix3d m1)
public final void setRotation(Matrix3f m1)
public final void setRotation(Quat4f q1)
public final void setRotation(Quat4d q1)
public final void setRotation(AxisAngle4f a1)
These methods set the rotational component (upper 3 x 3) of this matrix to the matrix values in the passed argument. The other elements of this matrix are unchanged. In the first two methods, a singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the passed rotation components, and finally the scale is reapplied to the rotational components. In the next two methods, a singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the matrix equivalent of the quaternion, and finally the scale is reapplied to the rotational components. In the last method, a singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the matrix equivalent of the axis-angle, and finally the scale is reapplied to the rotational components.
public final void setRotationScale(Matrix3f m1)
This method replaces the upper 3 x 3 matrix values of this matrix with the values in the matrix m1.
public final void setTranslation(Vector3f trans)
This method modifies the translational components of this matrix to the values of the vector trans. The other values of this matrix are not modified.
public final void setIdentity()
This method sets this Matrix4f to identity.
public final void setZero()
This method sets this matrix to all zeros.
public final void add(Matrix4f m1, Matrix4f m2)
public final void add(Matrix4f m1)
public final void sub(Matrix4f m1, Matrix4f m2)
public final void sub(Matrix4f m1)
The first add method adds the matrix m1 to the matrix m2 and places the result into the matrix this. The second add method adds the matrix this to the matrix m1 and places the result into the matrix this. The first sub method performs an element-by-element subtraction of matrix m2 from matrix m1 and places the result into the matrix this. The second sub method performs an element-by-element subtraction of the matrix m1 from the matrix this and places the result into the matrix this.
public final void transpose(Matrix4f m1)
public final void transpose()
The first transpose method transposes the matrix m1 and places the result into the matrix this. The second transpose method transposes the matrix this and places the result back into the matrix this.
public final void transform(Point3f point)
public final void transform(Point3f point, Point3f pointOut)
The first transform method postmultiplies this matrix by the Point3f point and places the result back into point. The multiplication treats the three-element point as if its fourth element were 1. The second transform method postmultiplies this matrix by the Point3f point and places the result into pointOut.
public final void transform(Vector3f normal)
public final void transform(Vector3f normal, Vector3f normalOut)
The first transform method postmultiplies this matrix by the Vector3f normal and places the result back into normal. The multiplication treats the three-element vector as if its fourth element were 0. The second transform method postmultiplies this matrix by the Vector3f normal and places the result into normalOut.
public final void transform(Tuple4f vec)
public final void transform(Tuple4f vec, Tuple4f vecOut)
The first transform method postmultiplies this matrix by the tuple vec and places the result back into vec. The second transform method postmultiplies this matrix by the tuple vec and places the result into vecOut.
public final void negate()
public final void negate(Matrix4f m1)
The first method negates the value of this matrix in place (this = -this). The second method sets the value of this matrix equal to the negation of the matrix m1 (this = -m1).
public final void invert()
public final void invert(Matrix4f m1)
The first method inverts this matrix in place. The second method sets the value of this matrix to the inverse of the matrix m1.
public final float determinant()
The determinant method computes the determinant of the matrix this and returns the computed value.
public final void rotX(float angle)
public final void rotY(float angle)
public final void rotZ(float angle)
The three rot methods construct rotation matrices that rotate in a counterclockwise (right-handed) direction around the axis specified as the last letter of the method name. The constructed matrix replaces the value of the matrix this. The rotation angle is expressed in radians.
public final void mul(Matrix4f m1, Matrix4f m2)
public final void mul(Matrix4f m1)
The first mul method multiplies matrix m1 with matrix m2 and places the result into the matrix this. The second mul method multiplies the matrix this with matrix m1 and places the result in matrix this.
public final void mulTransposeBoth(Matrix4f m1, Matrix4f m2)
public final void mulTransposeRight(Matrix4f m1, Matrix4f m2)
public final void mulTransposeLeft(Matrix4f m1, Matrix4f m2)
The mulTransposeBoth method multiplies the transpose of matrix m1 (left) times the transpose of matrix m2 (right) and places the result into this matrix. The mulTransposeRight method multiplies matrix m1 times the transpose of matrix m2 and places the result back into this matrix. The mulTransposeLeft method multiplies the transpose of matrix m1 times matrix m2 and places the result into this matrix.
public boolean equals(Matrix4f m1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Matrix4f m1 are equal to the corresponding data members in this Matrix4f. The second method returns true if the Object t1 is of type Matrix4f and all of the data members of t1 are equal to the corresponding data members in this Matrix4f.
public boolean epsilonEquals(Matrix4f m1, float epsilon)
This method returns true if the L distance between this Matrix4f and Matrix4f m1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to

MAX[i = 0,1,2,3; j = 0,1,2,3; abs(this.m(i,j) - m1.m(i,j)]
public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two different Matrix4f objects with identical data values (that is, equals(Matrix4f) returns true) will return the same hash number. Two Matrix4f objects with different data members may return the same hash value, although this is not likely.
public String toString()
The toString method returns a string that contains the values of this Matrix4f.

A.2.4 Matrix4d Class
The Matrix4d class serves to contain 4 x 4 matrices mainly for storing and manipulating 3D transformation matrices. The class includes nine different constructors for creating matrices and several operators for manipulating these matrices.

Variables
The component values of a Matrix4d are directly accessible through the public variables m00, m01, m02, m03, m10, m11, m12, m13, m20, m21, m22, m23, m30, m31, m32, and m33. To access the element in row 2 and column 0 of matrix rotate, a programmer would write rotate.m20. A programmer would access the other values similarly.
public double m00
public double m01
public double m02
public double m03
public double m10
public double m11
public double m12
public double m13
public double m20
public double m21
public double m22
public double m23
public double m30
public double m31
public double m32
public double m33
These public variables are the elements of the matrix.

Constructors
public Matrix4d(double m00, double m01, double m02, double m03,
       double m10, double m11, double m12, double m13, double  m20,
       double m21, double m22, double m23, double  m30, double m31,
       double m32, double m33)
public Matrix4d(double v[])
public Matrix4d(Quat4d q1, Vector3d t1, double s)
public Matrix4d(Quat4f q1, Vector3d t1, double s)
public Matrix4d(Matrix3d m1, Vector3d t1, double s)
public Matrix4d(Matrix3f m1, Vector3d t1, double s)
public Matrix4d(Matrix4d m1)
public Matrix4d(Matrix4f m1)
public Matrix4d()
Each of these constructors returns a new Matrix4d object. The first constructor generates a 4 x 4 matrix from the 16 values provided. The second constructor generates a 4 x 4 matrix from the first 16 values in the array v. The third through sixth constructors generate a 4 x 4 matrix from the quaternion, translation, and scale values. The scale is applied only to the rotational components of the matrix (upper 3 x 3) and not to the translational components. The seventh and eighth constructors generate a 4 x 4 matrix with the same values as the passed matrix. The final constructor generates a 4 x 4 matrix with all 16 values set to 0.0.

Methods
public final void get(Matrix3d m1)
public final void get(Matrix3f m1)
public final double get(Matrix3d m1, Vector3d t1)
public final double get(Matrix3f m1, Vector3d t1)
public final void get(Quat4f q1)
public final void get(Quat4d q1)
public final void get(Vector3d trans)
The first two methods perform an SVD normalization of this matrix in order to acquire the normalized rotational component. The values are placed into the passed parameter. The next two methods perform an SVD normalization of this matrix to calculate the rotation as a 3 x 3 matrix, the translation, and the scale. None of the matrix values is modified. The next two methods perform an SVD normalization of this matrix to acquire the normalized rotational component. The last two methods retrieve the translational components of this matrix.
public final void setElement(int row, int column, double value)
public final double getElement(int row, int column)
The setElement and getElement methods provide a means for accessing a single element within a 4 x 4 matrix using indices. This is not a preferred method of access, but Java 3D provides these methods for functional completeness. The setElement method takes a row index row (where a value of 0 represents the first row and a value of 3 represents the fourth row), a column index column (where a value of 0 represents the first column and a value of 3 represents the fourth column), and a value. It sets the corresponding element in matrix this to the specified value. The getElement method also takes a row index row and a column index column and returns the element at the corresponding locations as a floating-point value.
public final void setRow(int row, double x, double y, double z,
       double  w)
public final void setRow(int row, Vector4d v)
public final void setRow(int row, double v[])
public final void getRow(int row, Vector4d v)
public final void getRow(int row, double v[])
The three setRow methods provide a means for constructing a 4 x 4 matrix on a row basis. The row parameter determines which row the method invocation affects. A row value of 0 represents the first row and a value of 3 represents the fourth row. The first setRow method specifies the four new values as independent floating-point values. The second setRow method uses the values in the Vector4d v to update the matrix. The third setRow method uses the first four values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getRow methods copy the matrix values in the specified row into the array or vector parameter, respectively.
public final void setColumn(int column, double x, double y,
       double  z, double  w)
public final void setColumn(int column, Vector4d v)
public final void setColumn(int column, double v[])
public final void getColumn(int column, Vector4d v)
public final void getColumn(int column, double v[])
The three setColumn methods provide a means for constructing a 4 x 4 matrix on a column basis. The column parameter determines which column the method invocation affects. A column value of 0 represents the first column and a value of 3 represents the fourth column. The first setColumn method specifies the four new values as independent double-precision floating-point values. The second setColumn method uses the values in the Vector4d v to update the matrix. The third setColumn method uses the first four values in the array v to update the matrix. In all three cases the matrix affected is the matrix this. The two getColumn methods copy the matrix values in the specified column into the array or vector parameter, respectively.
public final void setRotation(Matrix3f m1)
public final void setRotation(Matrix3d m1)
These methods set the rotational component (upper 3 x 3) of this matrix to the matrix values in the passed argument. The other elements of this matrix are unchanged. A singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the passed rotation components, and finally the scale is reapplied to the rotational components.
public final void setRotation(Quat4f q1)
public final void setRotation(Quat4d q1)
These methods set the rotational component (upper 3 x 3) of this matrix to the matrix values in the passed argument. The other elements of this matrix are unchanged. A singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the matrix equivalent of the quaternion, and finally the scale is reapplied to the rotational components.
public final void setRotation(AxisAngle4d a1)
This method sets the rotational component (upper 3 x 3) of this matrix to the equivalent values in the passed argument. The other elements of this matrix are unchanged. A singular value decomposition is performed on this object's upper 3 x 3 matrix to factor out the scale, then this object's upper 3 x 3 matrix components are replaced by the matrix equivalent of the axis-angle, and finally the scale is reapplied to the rotational components.
public final void getRotationScale(Matrix3f m1)
public final void getRotationScale(Matrix3d m1)
public final void setRotationScale(Matrix3d m1)
public final void setRotationScale(Matrix3f m1)
The two get methods retrieve the upper 3 x 3 values of this matrix and place them into the matrix m1. The two set methods replace the upper 3 x 3 matrix values of this matrix with the values in the matrix m1.
public final void setTranslation(Vector3d trans)
This method modifies the translational components of this matrix to the values of the Vector3d argument. The other values of this matrix are not modified.
public final void setScale(double scale)
public final double getScale()
The first method sets the scale component of the current matrix by factoring out the current scale (by doing an SVD) and multiplying by the new scale. The second method performs an SVD normalization of this matrix to calculate and return the uniform scale factor. If the matrix has nonuniform scale factors, the largest of the x, y, and z scale factors will be returned.
public final void add(double scalar)
This method adds a scalar to each component of this matrix.
public final void add(double scalar, Matrix4d m1)
This method adds a scalar to each component of the matrix m1 and places the result into this. Matrix m1 is not modified.
public final void mul(double scalar, Matrix4d m1)
This method multiplies each component of the matrix m1 by a scalar and places the result into this. Matrix m1 is not modified.
public final void mul(double scalar)
This method multiplies each element of this matrix by a scalar.
public final void add(Matrix4d m1, Matrix4d m2)
public final void add(Matrix4d m1)
public final void sub(Matrix4d m1, Matrix4d m2)
public final void sub(Matrix4d m1)
The first add method adds the matrix m1 to the matrix m2 and places the result into the matrix this. The second add method adds the matrix this to the matrix m1 and places the result into the matrix this. The first sub method performs an element-by-element subtraction of matrix m2 from matrix m1 and places the result into the matrix this. The second sub method performs an element-by-element subtraction of the matrix m1 from the matrix this and places the result into the matrix this.
public final void set(double m[])
This method sets the value of this matrix to the row-major array parameter (that is, the first four elements of the array will be copied into the first row of this matrix, and so forth).
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
These methods set the rotational component (upper 3 x 3) of this matrix to the matrix values in the matrix argument. The other elements of this matrix are initialized as if this were an identity matrix (that is, an affine matrix with no translational component).
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
These methods set the value of this matrix to the value of the passed matrix m1.
public final void set(Quat4d q1)
public final void set(Quat4f q1)
These methods set the value of this matrix to the matrix conversion of the quaternion argument.
public final void set(AxisAngle4d a1)
public final void set(AxisAngle4f a1)
These methods set the value of this matrix to the matrix conversion of the axis and angle argument.
public final void set(Vector3d v1)
This method sets the value of this matrix to a translation matrix by the passed translation value.
public final void set(Quat4d q1, Vector3d t1, double s)
public final void set(Quat4f q1, Vector3d t1, double s)
public final void set(Quat4f q1, Vector3f t1, float s)
These methods set the value of this matrix to the rotation expressed by the quaternion q1, the translation t1, and the scale s.
public final void set(double scale)
This method sets the value of this matrix to a scale matrix with the passed scale amount.
public final void set(double scale, Vector3d v1)
This method sets the value of this matrix to a scale and translation matrix. The scale is not applied to the translation, and all of the matrix values are modified.
public final void set(Vector3d v1, double scale)
This method sets the value of this matrix to a scale and translation matrix. The translation is scaled by the scale factor, and all of the matrix values are modified.
public final void set(Matrix3f m1, Vector3f t1, float scale)
public final void set(Matrix3d m1, Vector3d t1, double scale)
These methods set the value of this matrix from the rotation expressed by the rotation matrix m1, the translation t1, and the scale s.
public final void negate(Matrix4d m1)
public final void negate()
The first method sets the value of this matrix to the negation of the m1 parameter. The second method negates the value of this matrix (this = -this).
public final void transpose(Matrix4d m)
public final void transpose()
The first transpose method transposes the matrix m and places the result into the matrix this. The second transpose method transposes the matrix this and places the result back into the matrix this.
public final void transform(Tuple4d vec)
public final void transform(Tuple4f vec)
public final void transform(Tuple4d vec, Tuple4d vecOut)
public final void transform(Tuple4f vec, Tuple4f vecOut)
The first two transform methods postmultiply this matrix by the tuple vec and place the result back into vec. The last two transform methods postmultiply this matrix by the tuple vec and place the result into vecOut.
public final void transform(Point3d point)
public final void transform(Point3f point)
public final void transform(Point3d point, Point3d pointOut)
public final void transform(Point3f point, Point3f pointOut)
The first two transform methods postmultiply this matrix by the point argument point and place the result back into point. The multiplication treats the three-element point as if its fourth element were 1. The last two transform methods postmultiply this matrix by the point argument point and place the result into pointOut.
public final void transform(Vector3d normal)
public final void transform(Vector3f normal)
public final void transform(Vector3d normal, Vector3d normalOut)
public final void transform(Vector3f normal, Vector3f normalOut)
The first two transform methods postmultiply this matrix by the vector argument normal and place the result back into normal. The multiplication treats the three-element vector as if its fourth element were 0. The last two transform methods postmultiply this matrix by the vector argument normal and place the result into normalOut.
public final void invert()
public final void invert(Matrix4d m1)
The first method inverts this matrix in place. The second method sets the value of this matrix to the inverse of the matrix m1.
public final double determinant()
The determinant method computes the determinant of the matrix this and returns the computed value.
public final void rotX(double angle)
public final void rotY(double angle)
public final void rotZ(double angle)
The rot methods construct rotation matrices that rotate in a counterclockwise (right-handed) direction around the axis specified as the last letter of the method name. The constructed matrix replaces the value of the matrix this. The rotation angle is expressed in radians.
public final void mul(Matrix4d m1, Matrix4d m2)
public final void mul(Matrix 4d m1)
The first mul method multiplies matrix m1 with matrix m2 and places the result into the matrix this. The second mul method multiplies matrix this with matrix m1 and places the result into the matrix this.
public final void mulTransposeBoth(Matrix4d m1, Matrix4d m2)
public final void mulTransposeRight(Matrix4d m1, Matrix4d m2)
public final void mulTransposeLeft(Matrix4d m1, Matrix4d m2)
The mulTransposeBoth method multiplies the transpose of matrix m1 (left) times the transpose of matrix m2 (right) and places the result into this matrix. The mulTransposeRight method multiplies matrix m1 times the transpose of matrix m2 and places the result back into this matrix. The mulTransposeLeft method multiplies the transpose of matrix m1 times matrix m2 and places the result into this matrix.
public final void setZero()
This method sets this matrix to all zeros.
public final void setIdentity()
This method sets this Matrix4d to identity.
public boolean equals(Matrix4d m1)
public boolean equals(Object t1)
The first method returns true if all of the data members of Matrix4d m1 are equal to the corresponding data members in this Matrix4d. The second method returns true if the Object t1 is of type Matrix4d and all of the data members of t1 are equal to the corresponding data members in this Matrix4d.
public boolean epsilonEquals(Matrix4d m1, float epsilon)
Deprecated method. See the next method.
public boolean epsilonEquals(Matrix4d m1, double epsilon)
This method returns true if the L distance between this Matrix4d and Matrix4d m1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to

MAX[i = 0,1,2,3; j = 0,1,2,3; abs(this.m(i,j) - m1.m(i,j)]
public int hashCode()
The hashCode method returns a hash number based on the data values in this object. Two different Matrix4d objects with identical data values (that is, equals(Matrix4d) returns true) will return the same hash number. Two Matrix4d objects with different data members may return the same hash value, although this is not likely.
public String toString()
The toString method returns a string that contains the values of this Matrix4d.

A.2.5 GMatrix Class
The GMatrix class serves to contain a double-precision, general, and dynamically resizeable M x N matrix. Row and column numbering begins with zero. The representation is row major.
The GMatrix data members are not public, thus allowing efficient implementations of sparse matrices. However, the data members can be modified through public accessors. The class includes three different constructors for creating matrices and several operators for manipulating these matrices.

Constructors
public GMatrix(int nRow, int nCol)
public GMatrix(int nRow, int nCol, double matrix[])
public GMatrix(GMatrix matrix)
Each of these constructors returns a new GMatrix. The first constructor generates an nRow by nCol identity matrix. Note that because row and column numbering begins with zero, nRow and nCol will be one larger than the maximum possible matrix index values. The second constructor generates an nRow by nCol matrix initialized to the values in the array matrix. The last constructor generates a new GMatrix and copies the initial values from the parameter matrix argument.

Methods
public final void mul(GMatrix m1, GMatrix m2)
public final void mul(GMatrix m1)
The first mul method multiplies matrix m1 with matrix m2 and places the result into this. The second mul method multiplies this matrix with matrix m1 and places the result into this.
public final void add(GMatrix m1)
public final void add(GMatrix m1, GMatrix m2)
public final void sub(GMatrix m1)
public final void sub(GMatrix m1, GMatrix m2)
The first add method adds this matrix to matrix m1 and places the result back into this. The second add method adds matrices m1 and m2 and places the result into this. The first sub method subtracts matrix m1 from the matrix this and places the result into this. The second sub method subtracts matrix m2 from matrix m1 and places the result into the matrix this.
public final void negate()
public final void negate(GMatrix m1)
The first method negates the value of this matrix in place (this = -this). The second method sets the value of this matrix to the negation of the matrix m1 (this = -m1).
public final void invert()
public final void invert(GMatrix m1)
The first method inverts this matrix in place. The second method sets the value of this matrix to the inverse of the matrix m1.
public final void setIdentity()
This method sets this GMatrix to the identity matrix.
public final void setZero()
This method sets all the values in this matrix to zero.
public final void identityMinus()
This method subtracts this matrix from the identity matrix and puts the values back into this (this = I - this).
public final void copySubMatrix(int rowSource, int colSource,
       int  numRow, int numCol, int rowDest, int colDest,
       GMatrix  target)
This method copies a submatrix derived from this matrix into the target matrix. The rowSource and colSource parameters define the upper left of the submatrix. The numRow and numCol parameters define the number of rows and columns in the submatrix. The submatrix is copied into the target matrix starting at (rowDest, colDest). The target parameter is the matrix into which the submatrix will be copied.
public final void setSize(int nRow, int nCol)
This method changes the size of this matrix dynamically. If the size is increased, no data values will be lost. If the size is decreased, only those data values whose matrix positions were eliminated will be lost.
public final void set(double matrix[])
public final void set(GMatrix m1)
public final void set(Matrix3f m1)
public final void set(Matrix3d m1)
public final void set(Matrix4f m1)
public final void set(Matrix4d m1)
The first set method sets the values of this matrix to the values found in the matrix array parameter. The values are copied in one row at a time, in row-major fashion. The array should be at least equal in length to the number of matrix rows times the number of matrix columns in this matrix. The second set method sets the values of this matrix to the values found in matrix m1. The last four set methods set the values of this matrix to the values found in matrix m1.
public final void get(Matrix3d m1)
public final void get(Matrix3f m1)
public final void get(Matrix4d m1)
public final void get(Matrix4f m1)
public final void get(GMatrix m1)
The first two methods place the values in the upper 3 x 3 of this matrix into the matrix m1. The next two methods place the values in the upper 4 x 4 of this matrix into the matrix m1. The final method places the values in this matrix into the matrix m1. Matrix m1 should be at least as large as this matrix.
public final int getNumRow()
public final int getNumCol()
The getNumRow method returns the number of rows in this matrix. The getNumCol method returns the number of columns in this matrix.
public final void setElement(int row, int column, double value)
public final double getElement(int row, int column)
These methods set and retrieve the value at the specified row and column of this matrix.
public final void setRow(int row, double array[])
public final void setRow(int row, GVector vector)
public final void getRow(int row, double array[])
public final void getRow(int row, GVector vector)
public final void setColumn(int col, double array[])
public final void setColumn(int col, GVector vector)
public final void getColumn(int col, double array[])
public final void getColumn(int col, GVector vector)
The setRow methods copy the values from the array into the specified row of this matrix. The getRow methods place the values of the specified row into the array or vertex. The setColumn methods copy the values from the array into the specified column of this matrix or vector. The getColumn methods place the values of the specified column into the array or vector.
public final void setScale(double scale)
This method sets this matrix to a uniform scale matrix, and all of the values are reset.
public final void mulTransposeBoth(GMatrix m1, GMatrix m2)
public final void mulTransposeRight(GMatrix m1, GMatrix m2)
public final void mulTransposeLeft(GMatrix m1, GMatrix m2)
The mulTransposeBoth method multiplies the transpose of matrix m1 (left) times the transpose of matrix m2 (right) and places the result into this matrix. The mulTransposeRight method multiplies matrix m1 times the transpose of matrix m2 and places the result back into this matrix. The mulTransposeLeft method multiplies the transpose of matrix m1 times matrix m2 and places the result into this matrix.
public final void transpose()
public final void transpose(GMatrix m1)
The first transpose method transposes this matrix in place. The second transpose method places the matrix values of the transpose of matrix m1 into this matrix.
public String toString()
This method returns a string that contains the values of this GMatrix.
public int hashCode()
This method returns a hash number based on the data values in this object. Two different GMatrix objects with identical data values (that is, equals(GMatrix) returns true) will return the same hash number. Two objects with different data members may return the same hash value, although this is not likely.
public boolean equals(GMatrix m1)
public boolean equals(Object o1)
The first method returns true if all of the data members of GMatrix m1 are equal to the corresponding data members in this GMatrix. The second method returns true if the Object o1 is of type GMatrix and all of the data members of o1 are equal to the corresponding data members in this GMatrix.
public boolean epsilonEquals(GMatrix m1, float epsilon)
Deprecated method. See the next method.
public boolean epsilonEquals(GMatrix m1, double epsilon)
This method returns true if the L distance between this GMatrix and GMatrix m1 is less than or equal to the epsilon parameter. Otherwise, this method returns false. The L distance is equal to

MAX[i = 0,1,2, ... n; j = 0,1,2,... n; abs(this.m(i,j) - m1.m(i,j)]
public final double trace()
This method returns the trace of this matrix.
public final int SVD(GMatrix U, GMatrix W, GMatrix V)
The SVD method finds the singular value decomposition (SVD) of this matrix such that this = U * W * V^T, and returns the rank of this matrix. The values of U, W, and V are all overwritten. Note that the matrix V is output as V and not V^T. If this matrix is m x n, then U is m x m, W is a diagonal matrix that is m x n, and V is n x n. The inverse of this matrix is this^-1 = V * W^-1 * U^T, where W^-1 is a diagonal matrix computed by taking the reciprocal of each of the diagonal elements of matrix W.
public final int LUD(GMatrix LU, GVector permutation)
The LUD method performs an LU decomposition. This matrix must be a square matrix, and the LU parameter must be the same size as this matrix. The diagonal elements of L (unity) are not stored. The permutation parameter records the row permutation affected by the partial pivoting and is used as a parameter to the GVector LUDBackSolve method to solve sets of linear equations. This method returns +1 or -1, depending on whether the number of row interchanges was even or odd, respectively.

The Java 3D API Specification

A.1.1.2 Vector2d Class

A.1.2.2 Vector2f Class

A.2.1 Matrix3f Class

Copyright © 2000, Sun Microsystems, Inc. All rights reserved.