 |
Flexible G1 Interpolation of Quad Meshes
Published in Graphical Models (Elsevier). Download bibtex.
http://dx.doi.org/10.1016/j.gmod.2014.09.001
Abstract:
Transforming an arbitrary mesh into a smooth G1 surface has been the subject of intensive research works. To get a visual pleasing shape without any imperfection even in the presence of extraordinary mesh vertices is still a challenging problem in particular when interpolation of the mesh vertices is required. We present a new local method, which produces visually smooth shapes while solving the interpolation problem. It consists of combining low degree biquartic Bézier patches with minimum number of pieces per mesh face, assembled together with G1-continuity. All surface control points are given explicitly. The construction is local and free of zero-twists. We further show that within this economical class of surfaces it is however possible to derive a sufficient number of meaningful degrees of freedom so that standard optimization techniques result in high quality surfaces.
Paper in high res (55Mb, author manuscript)
Paper in low res (3Mb, author manuscript)
Results:
In the following Table several results are given in standard ascii files so that they can be inspected with your own software tools.
The input quad meshes (4th column) were generated from the collection of meshes by Cindy Grimm
Bézier files (5th column) are Ascii files with the number N of quartic patches (one integer) followed by 25xN Bézier control-points.
The uniformly tesselated surfaces (6th column) were obtained by evaluating the Bézier patches on a regular grid of isoparametric lines. Furthermore these files contain the exact continuous normal of the G1 interpolating surface.
obj files can be viewed with Blender or Meshlab
Name |
Quad mesh |
G1 Interpolating Surface |
Quad mesh file |
Bezier file |
Uniformly Tesselated surface with exact normals (obj file) |
Apple |
 |
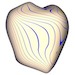 |
|||
Vase |
 |
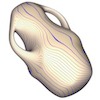 |
|||
Gumby1 |
 |
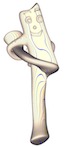 |
|||
Gumby2 |
 |
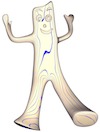 |
|||
Gumby3 |
 |
 |