 |
Ce premier chapitre d'état de l'art décrit les méthodes de simplification. Il motive ainsi les méthodes procédurales, plus rares et plus proches de nos propres travaux, dont l'état de l'art sera fait au chapitre suivant.
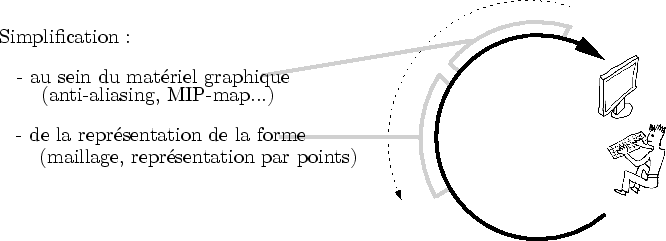
Les méthodes de simplification agissent à différents moments du processus de création (cf. figure 2.1). Nous les décrirons dans l'ordre inverse du flux d'information envoyé par le créateur. Nous commencerons par les méthodes de simplification prenant place au sein même de la carte graphique. Nous continuerons par celles s'appliquant à la représentation du modèle dans le processeur central.
Notons ici que cette partie, et tout ce mémoire de thèse en général, se place dans le contexte d'une utilisation intensive des cartes graphiques actuelles. Celles-ci sont toutes basées sur une architecture en pipe-line et sur un flux d'information monodirectionnel. Des formes géométriques simples sont décomposées en fragments qui vont s'amonceler sur le tampon de couleur [WND99]. Une connaissance de ces mécanismes est fortement recommandée pour la lecture de ce document.
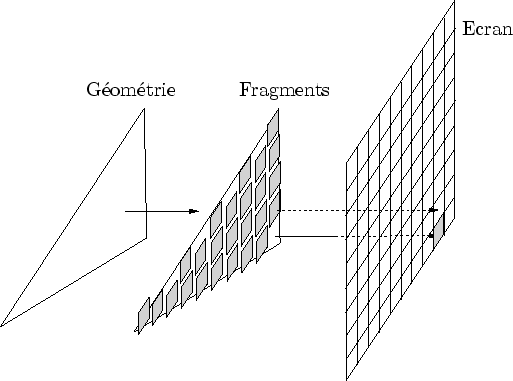
Tout à la fin du processus de création (cf. figure 2.1), au moment du rendu final, l'information envoyée par le créateur existe au sein de la carte graphique sous une forme brute : les fragments et les pixels (cf. figure 2.2). À ce niveau, les difficultés posées par l'affichage d'objets vus à différentes échelles sont connues sous le nom d'aliasing.
Après une rapide description des problèmes causés par l'aliasing, nous décrirons les méthodes d'anti-aliasing. Nous listerons ensuite d'autres techniques susceptibles de prendre en charge une partie du problème. Nous conclurons en identifiant les raisons pour lesquelles le matériel graphique ne peut pas, à lui tout seul, résoudre les problèmes posés par la multi-échelle.
 |
Lorsque la résolution de la projection d'un modèle 3D sur l'écran est très différente de la résolution de la grille de pixels de l'écran, la qualité de l'affichage est parasitée. Lorsque cette Ce phénomène est appelé aliasing.
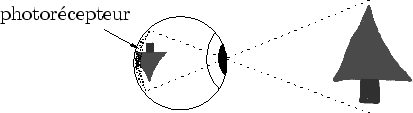
Dans le monde réel, nos yeux traitent très efficacement tous les signaux qu'ils reçoivent. Les récepteurs tapis au fond de la rétine réagissent aux photons lui parvenant et filtre ce signal spatialement et temporellement (cf. figure 2.3). Ce filtrage, qui est une sorte de simplification, s'effectue à coût constant et ne dépend pas de la complexité du monde observé.
 |
Dans les mondes virtuels que nous générons, cela ne se passe pas de la même manière.
Tout d'abord, le monde n'existe pas au sens ``physique'' du terme.
Il est remplacé par des données qui sont transformées tout le long du processus de création (cf. figure 2.1) pour finalement devenir des pixels sur l'écran.
L'écran et la carte graphique sont en quelque sorte un 
il intermédiaire qui observe le monde virtuel et qui est lui-même observé par le créateur.
L'écran joue ici le rôle d'il ``intermédiaire''.
L'onde lumineuse devient une métaphore du flux d'informations que génère l'algorithme.
Ce flux, juste avant de percuter l'écran, existe sous la forme de fragments, c'est-à-dire d'éventuels futurs pixels.
Les difficultés liées à ce fonctionnement résident essentiellement dans la discrétisation de l'écran.
Revenons un instant au monde réel : les récepteurs de la rétine filtrent le signal lumineux quelque soit sa complexité. Cette intégration est essentielle et nous permet d'apprécier une valeur représentative d'un signal infiniment plus complexe issu de la réalité. En effet, les ondes lumineuses du monde réel sont beaucoup plus complexes que celle que nos yeux envoient au cerveau. Par exemple, lorsque nous regardons un tee-shirt rose, les photons qui viennent vers notre oeil sont descriptifs de détails très précis tel que les fibres ou même plus. En revanche, le signal que nos yeux envoient au cerveau est qu'une surface lisse et de couleur quasi-uniforme : les fibres ont disparues au profit d'un signal grossier mais néanmoins représentatif, c'est à dire rose.
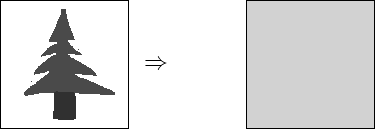
Dans les mondes virtuels, ce filtrage est tout aussi importante et les pixels allumés sur l'écran doivent absolument être représentatifs du signal plus précis tel qu'il a été décrit par le créateur (cf. figure 2.4). D'une façon ou d'une autre, il faut donc retrouver, lors de l'observation, la précision qui correspond le mieux à cette observation. Pourtant, le créateur ignore à quelle précision va être observée la forme qu'il crée. Il doit donc faire en sorte que cette forme soit adaptative et puisse passer d'une précision à l'autre.
 |
Venons en à des considérations plus techniques. La synthèse d'images, en un sens, n'est ni plus ni moins que l'art de discrétiser des fonctions sur une grille régulière : l'écran. La difficulté vient du fait que l'on ne désire pas vraiment calculer la fonction en chacun des points de l'écran, mais sur la surface des petits carrés que constitue chaque pixel. C'est donc une sorte d'intégrale des couleurs qu'il est nécessaire de faire en chacun des pixels.
Par exemple, si trop de fragments (de candidats au pixel) viennent sur un même pixel, de sérieux problèmes surgissent. Le pixel ne sait plus que faire de toute cette information et décide plus ou moins aléatoirement de celle qui sera finalement retenue. Il commettra ainsi une erreur à chaque affichage. De plus, rien n'assure que cette erreur reste la même d'un affichage à l'autre. Cela conduit irrémédiablement à des clignotements qui détériorent la qualité du rendu. On obtient alors autre chose que ce que l'on souhaitait, d'où l'utilisation de l'expression : problème d'aliasing (la base latine de "alias" signifiant "autre"). Une traduction française d'aliasing pourrait d'ailleurs être altération.
Pour lutter contre l'aliasing, de nombreuses méthodes ont été mises au point. Notamment, le sous-ensemble de ces méthodes traitant l'information quasiment au niveau des pixels est nommé anti-aliasing. Il est amusant de constater que toutes les méthodes luttant contre l'aliasing n'ont pas droit à cette noble appellation. Peut-être est-ce rassurant de cantonner ce problème loin de l'Homme dans le processus de création. Une façon de dire, peut-être, que «c'est la faute de l'ordinateur si ça ne marche pas»...
Nous verrons dans ce chapitre comment, en voulant à tout prix éviter l'aliasing, de nombreuses méthodes ont remonté progressivement tout le processus de création pour finalement nous toucher directement. Bien entendu, ce n'est pas l'ordinateur le fautif. Les causes du problème prennent leur source dans notre cerveau, dans la simple manière dont nous élaborons un modèle virtuel observable à différentes échelles (cf. chapitre suivant).
De nombreux fragments transitent vers le tampon de couleur dans l'espoir de devenir pixel. Quand plusieurs fragments revendiquent la place, les problèmes d'aliasing apparaissent. Afin d'y pallier, il faut trouver un moyen de relaxer un peu le critère de choix et de choisir non plus un fragment, mais plusieurs fragments dont l'influence est judicieusement pondérée.
Comment assurer un rendu correct d'une information échantillonnée trop finement pour les pixels de l'écran? La réponse théorique, contrairement à sa mise en pratique, est simple : il suffit d'augmenter la précision de l'écran. Physiquement, bien sûr, c'est impossible. Mais on peut toujours imaginer des algorithmes permettant de simuler un écran virtuel avec des pixels plus petits que ceux de l'écran réel. Pour revenir à l'écrean réel, il suffirait de filtrer en intégrant tout les sous-pixels virtuels dans le pixel réel correspondant. Ainsi, après un filtrage adéquat de l'écran virtuel on retrouverait la taille de l'écran réel et on supprimerait les effets indésirables du sur-échantillonnage.
Mais le coût mémoire d'un tel écran virtuel ainsi que le coût temporel de la fonction de filtrage rend impossible une telle réalisation avec un facteur d'échelle trop important.
Supposons par exemple que la géométrie soit 10 fois plus petite que la taille du cône de vision d'un pixel (cf. figure 2.5).
Un écran virtuel devrait alors être 10 fois plus grand pour espérer obtenir une bonne valeur pour chaque pixel, ce qui amènerait sa taille à
2.1.
Pour un facteur 100 (les feuilles d'une forêt vues de la montagne avoisinante), la taille mémoire devient 
.
Ces coûts mémoires rendent l'idée irréalisable.
 |
Certaines approches accumulent la valeur de fragments concurrents dans un même pixel de l'écran [HA90]. Celui-ci intègre successivement ces nouveaux fragments à la couleur du pixel. Ces techniques résolvent en partie les problèmes de coût exposés plus haut puisque l'écran garde la même taille. Néanmoins, il est délicat de savoir quelle importance donner à tel ou tel fragment, puisque l'information sur la couverture du pixel est perdue (les fragments sont comme des points, il n'ont pas de taille).
Il est possible de garder une bonne approximation de l'information de couverture en générant des fragments dédiés à une sous-partie d'un pixel.
Notamment, le A-buffer [Car84] propose de découper un pixel en sous-parties (le plus souvent
).
De cette façon, il devient possible de mieux quantifier l'influence de chaque fragment et de calculer une couleur finale relativement correcte.
L'implémentation de ce genre de techniques ne supporte le temps-réel que lorsqu'elle est directement coulée dans le silicium. De fait, les cartes graphiques récentes proposent des méthodes efficaces améliorant très sensiblement la qualité du rendu. Malheureusement, le facteur d'échelle gagné est de l'ordre de la dizaine, bien loin des buts que nous nous sommes fixés dans le chapitre 1. Dans le cas contraire, la mémoire et les coûts de calcul explosent.
Les méthodes d'anti-aliasing ont évidemment leur utilité et participent notamment à combattre d'autre phénomènes d'aliasing qui ne sont pas liées à la multi-échelle (tel que le crénelage). Cependant, elle ne sont pas suffisantes, à elles-seules, pour afficher des scènes complexes observables à différentes échelles.
Une autre forme d'aliasing sévit tous les jours sur nos écrans, mais elle n'a ordinairement pas le privilège d'être étiquetée comme produit de l'aliasing : il s'agit du sous-échantillonnage (c'est-à-dire l'inverse du sur-échantillonnage). Par exemple, prenez un lapin rouge. Vu à une certaine distance, le lapin rouge ressemble à un lapin rouge, ce qui est très souhaitable. Mais rapprochons nous maintenant, si bien que tout l'écran devient uniformément rouge. On ne voit plus un lapin, ni ses poils que l'on aurait dù voir pourtant. On voit autre chose : du rouge. Donc, si l'on se réfère à l'étymologie du mot, c'est bien d'aliasing dont il s'agit.
Sans doute l'appellation paraît inappropriée car, finalement, on s'attend bien à voir un écran rouge, comment en serait-il autrement? Si les poils n'ont pas été modélisés, l'ordinateur ne pourra pas les inventer. C'est donc moins surprenant de voir un écran rouge que le désagréable clignotement de l'aliasing dû au sur-échantillonnage. Mais mis à part cette considération émotionnelle, il s'agit bien, scientifiquement, des deux faces du même problème.
 |
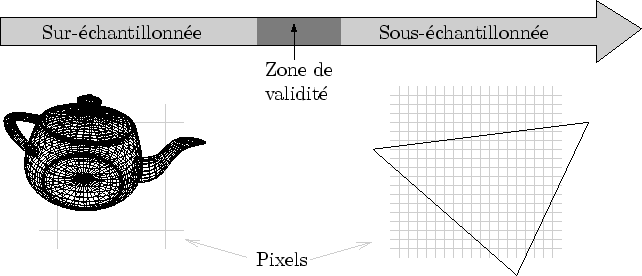Il n'est pas vraiment de remède miracle au sous-échantillonnage. Les modèles géométriques courants sont implicitement créés pour être observés à une certaine échelle. Si l'on observe de plus près, on peut toujours filtrer et simplifier l'information. Mais si l'on observe de plus loin, on touche aux limites du modèle et incidemment à la ``stupidité'' d'un ordinateur : celui-ci est bien incapable d'automatiquement enrichir une forme visible sans qu'on lui ai dit comment faire. Un modèle pré-échantillonné n'est donc valable que dans une certaine zone d'observation en dehors de laquelle il devient caduque (cf. figure 2.6).
Avant de conclure sur l'affichage multi-échelle au sein des cartes graphiques dans la sous-section suivante, nous expliquons ici deux approches communément utilisées pour réduire les problèmes d'aliasing. Elles ne sont pourtant pas étiquetées comme méthodes d'anti-aliasing. Il s'agit du MIP-mapping (discrétisé) et de la programmabilité (procédurale).
Les textures sont des tableaux2.2 échantillonnés régulièrement. Elles représentent la plupart du temps certaines propriétés de la fonction d'éclairage tel que le spectre de diffusion (autrement dit, les couleurs) ou une direction privilégiée (les normales). Une texture est appelée par un fragment qui, nous l'avons vu plus haut (cf. figure 2.2), peut représenter une zone plus ou moins vaste. Par exemple, un fragment peut représenter à lui seul toute la texture. Il est donc nécessaire d'intégrer l'information afin d'obtenir une valeur du fragment correcte, c'est-à-dire représentative de toute la portion de texture qu'il recouvre.
De nombreuse méthodes opèrent un pré-traitement sur ces tableaux afin de construire une hiérarchie de textures plus ou moins fine. Ces opérations sont connus sous le nom de MIP-mapping[Wil83]. L'acronyme MIP vient de l'expression latine "multim in parvo" qui veut dire "beaucoup de chose dans une petite place". Pour les tableaux à une et deux dimensions, le MIP-mapping réduit efficacement les parasites dus à un mauvais échantillonnage. Les récentes fonctions de filtrage anisotrope ajoutent encore à la qualité du rendu.
Les méthodes de MIP-mapping ressemble aux méthodes d'anti-aliasing dans la mesure où elles s'appliquent à des données régulièrement échantillonnées. Compte tenu du fait qu'il s'applique à des données statiques (les textures ne sont pas modifiées à chaque affichage), on peut décrire le MIP-mapping comme une sorte de pré-anti-aliasing local. Le terme ``local'' vient du fait que ces méthodes ne s'appliquent pas à tout l'écran, mais à chacune des textures des différents objets constituant la scène.
Les fragments issus d'une primitive graphique sont autant d'approximations de la fonction d'éclairage du matériau. Performance oblige, il n'est pas question de s'amuser à décrire la micro-structure d'une surface et à l'intégrer lors de l'affichage. Un éventail de fonctions d'éclairage permet de calculer efficacement quelques comportements simplistes (éclairage diffus, spéculaire). Cette modélisation procédurale de l'éclairage a fait ses preuves. Mais elle est insuffisante pour représenter des éclairages complexes et réalistes.
La sophistication de ces fonctions d'éclairage a récemment fait un bond en avant avec les fragment-programs [WND99]. Ces micro-programmes permettent notamment d'augmenter l'éventail des fonctions d'éclairage. Ils le font de manière procédurale alors que les textures que nous venons d'évoquer s'attaquent au même problème (enrichir la fonction d'éclairage) mais de manière discrétisée.
Plus généralement, la programmabilité des cartes graphiques récentes offre une souplesse qui peut être utilisée pour mieux gérer la multi-échelle. Par exemple, [DVS03] utilise les vertex-programs pour déterminer quelle hiérarchie de point doit être utilisée pour l'affichage courant. [BS04] propose une génération de surfaces de subdivision avec un fragment-program. Même si les traitements réalisés en hardware restent relativement simples, il est clair que ces approches procédurales sont très prometteuses.
Le matériel graphique fait parfois la pluie et le beau temps en synthèse d'images. En divisant par cent le coût de certaines fonctions, il peut éventuellement rendre complètement obsolètes certains algorithmes ou au contraire les remettre aux goûts du jour. Indéniablement, la recherche en infographie dépend, dans une certaine mesure, des possibilités offertes par les cartes graphiques (de même qu'elle dépend de toute l'architecture d'un ordinateur). Mais il est important de garder la tête froide : voyons pourquoi on ne peut pas tout attendre d'un matériel spécialisé.
Plus l'information migre le long du processus de création, moins celle-ci est sophistiquée. Par exemple, en fin de course, l'information devient une vaste énumération de pixels mis à jour plusieurs dizaines de fois par seconde. En début de cycle, l'idée d'un modèle qui germe dans notre cerveau est une information de nature bien plus sophistiquée et concise qu'une simple énumération. La création revient à trouver un moyen de transformer la représentation du modèle tout en la gardant fidèle à l'idée de départ.
En fin de parcours, la carte graphique s'occupe du traitement final de l'information. Compte tenu de la simplicité de la représentation finale, les traitements sont très basiques (projection, rasterisation). En revanche, ils sont redoutablement efficaces et traitent une très grande quantité d'informations. Ce mélange d'efficacité et de simplicité est la nature profonde des cartes graphiques.
Dans cette section, nous avons vu que les cartes graphiques étaient d'un grand secours face au problème posé par la multi-échelle. Mais, de par leur nature ``simple et efficace'', elles ne prendront jamais complètement en charge un problème aussi complexe que celui du rendu multi-échelle de scène complexe animée.
Bien qu'elles soient parfois utilisées pour des tâches qui n'ont rien de visuel [BFGS03], elles ne peuvent offrir autant de souplesse qu'un processeur universel. Certains pensent que ces cartes sont les prémices d'un nouveau type de processeur universel basé sur un flux d'information intense et redirectionnel. Ces considérations sont alléchantes et laissent entrevoir une toute autre utilisation des cartes graphiques (mais peut-être ne seront-elles alors plus appelées comme ça).
Plutôt que de spéculer sur l'avenir des GPU, revenons en à la multi-échelle. J'affirme que la complexité algorithmique nécessaire au rendu multi-échelle de scènes complexes et animées dépasse de loin les possibilité des cartes graphiques actuelles. Évidemment, plus il sera possible de migrer des fonctionnalités au sein du GPU, plus efficace sera l'affichage. Néanmoins, il restera toujours un noyau algorithmique qui ne pourra être réalisé que sur un support suffisamment complexe et souple tel que le processeur universel. L'une des contributions de cette thèse est l'identification de ce noyau ainsi qu'une tentative d'implémentation (chapitre 3).
Plus en amont dans le processus de création, pendant ou juste après la modélisation, une forme visible peut être décrite par de nombreuses représentations : maillage, volume, surfels... Généralement, pour chacune de ces représentations, plusieurs méthodes de simplification permettent un affichage multi-échelle.
Avant tout, nous commencerons par définir ce que nous entendons par simplification. Nous décrirons ensuite rapidement les différentes méthodes de simplification générique. Ensuite, nous décrirons les limites de ces méthodes dans le cadre de la modélisation et du rendu de scènes animées avec de grandes variations d'échelle.
Les méthodes de simplification calculent automatiquement des versions plus grossière d'un modèle décrit à son niveau le plus fin.
Nous caractérisons les méthodes de simplification par le fait qu'elles prennent en donnée d'entrée un modèle supposé être au niveau le plus fin pour calculer des versions plus grossière (moins précise). La quasi-totalité des modeleurs classiques (Maya ou 3DSMAX par exemple) produisent justement des modèles décrits à leur niveau le plus fin. Par conséquent, les méthodes de simplification sont très majoritaires dans l'ensemble des travaux proposant une approche multi-échelle.
Les méthodes de simplification se veulent automatiques : l'utilisateur fournit simplement le modèle en entrée et récupère le résultat. Ce but est louable car les méthodes de simplification interviennent une fois la modélisation terminée2.3.
De nombreuses représentations permettent de décrire des formes visibles. Les méthodes de simplification sont ici classées en fonction de la représentation à laquelle elles s'appliquent. Cette classification restera très générale : mon propos est plutôt de monter l'inadéquation de l'approche d'un point de vue global.
Les maillages sont la représentation la plus utilisée et détiennent haut la main le record du nombre d'algorithmes de simplification [Hop97,RB93]... Je vous renvoie à l'excellent [LRC+02] qui recense la quasi-totalité des méthodes de simplification de maillages.
De notre point de vue, les principales caractéristiques de ces méthodes sont :
Seuls les algorithmes à précision variable peuvent supporter un affichage avec de grandes variations d'échelle. La gène visuelle occasionnée par des transitions discrètes [Red97] limite leur emploi intensif.
Les représentations volumiques [KK89,Ney98] décrivent une forme visible par un échantillonnage spatial de la fonction d'éclairage. Des versions plus efficaces ont été proposées [LL94], parfois supportées par le matériel graphique [MN98].
En fonction du type d'information stocké dans un texel, les représentations volumiques permettent des simplifications plus ou moins importante. Par exemple, le codage de l'opacité d'un texel permet d'engendrer des versions grossières du modèle de bonne qualité [HHK+95]. Les représentations volumiques supportent donc mieux les simplifications extrêmes. En revanche, le passage à la 3D entraîne souvent des coûts mémoires nettement supérieurs aux représentations maillées.
Le terme représentations alternatives [Ney01] caractérise des méthodes de représentations originales, par exemple :
par des images simplifie énormément la complexité d'une scène [DDSD03,CBL99,MS95,LS97].
Dans le cadre de scènes animées observées avec de grandes variations d'échelle, la simplification souffre principalement de trois limitations.
La simplification extrême de formes lest un problème très délicat. Dans la grande majorité des cas, la qualité de l'approximation se dégrade fatalement à partir d'un certain degré de simplification. Imaginons par exemple un livre dont une face (la couverture) est rouge et l'autre face est verte. Très peu d'algorithmes, lors d'une simplification extrême, réduiront le livre à une sorte de point dont la couleur variera selon le point de vue.
Certaines représentations s'en sortent mieux que d'autres. Notamment, les représentations volumiques ou les light fields prenant en compte la transparence sont très robustes. En revanche, les coûts mémoires nécessaire pour décrire de grandes scènes deviennent vite insupportables. En fait, cette robustesse est réalisée au détriment de tout codage ingénieux du modèle. En effet, l'intelligence d'une représentation repose sur la connaissance du ``type'' de la forme (lisse, chaotique, transparent...). Mais ce type à la fâcheuse tendance de changer complètement lors de passages à l'échelle (une prairie vue de très loin est une surface lisse).
La simplification automatique révèle ici ses limites : sa méconnaissance sémantique des structures qu'elle manipule. Non seulement, comme nous venons de le voir, la nature de l'objet lui échappe, mais elle ignore aussi l'importance que nous, humains, accordons à cet objet. Par exemple, il nous est bien égal qu'un algorithme approxime brutalement un caillou au bord de la route. En revanche, il devra prêter une grande attention à la simplification des yeux humains. Nous remarquerions en effet la moindre dissymétrie, même de loin. En fait, la simplification de forme visible peut supporter une part d'automatisme mais elle ne pourra jamais fonctionner pour un large type d'objets et pour des grandes variations d'échelle sans une intervention humaine. Nous seuls sommes capables de décréter ce qui est important à nos yeux.
La connaissance explicite d'une scène à son niveau le plus fin limite drastiquement tout codage ingénieux. Nul besoin d'aller à des échelles astronomiques, les moindres paysages un peu trop volumineux sont très vite impossibles à stocker. En effet, les données d'entrée (le modèle à sa précision maximum) se chiffrent rapidement en dizaines ou centaines de gigaoctets.
Certaines méthodes de pagination de donnée transforment le disque dur en une extension plus lente mais plus volumineuse de la mémoire vive [LP02]. Les structures de données utilisées sont de plus en plus sophistiquées et accélèrent l'accès aux données. Mais cela ne fait que repousser le problème. D'ailleurs, on peut toujours décréter que l'on veut traiter des scènes de taille infinie (comme les fractales).
Le constat est clair : en utilisant une description au niveau le plus fin, on limite la taille des scènes visualisables. Cette limite est floue et dépend notamment de la représentation choisie. Il est donc difficile de quantifier à partir de quand ce handicap devient trop pesant. Mais dans une optique de rendu avec de grandes variations d'échelle, la simple existence de cette limite est très rebutante.
Les algorithmes de simplification temps-réel utilisent systématiquement un précalcul dont le but est de permettre un rendu efficace. Ces précalculs représentent toujours plus ou moins une représentation du modèle à différentes résolutions. Si la forme du modèle change (par exemple, lors d'une animation), il doit donc remettre à jour toute l'information plus grossière qui dépend de la zone qui s'est déformée. Le coût de cette mise à jour est souvent incompatible avec un affichage temps-réel.
En pratique, l'utilisation d'algorithmes de simplification limite beaucoup les possibilités d'animation. Dans certaines scènes très statiques, cela ne pose pas vraiment de problème (comme les villes). Mais c'est incompatible avec notre objectif : le rendu de scènes animées avec de grandes variations d'échelle (dans le film «Dark city», les bâtiments changent de place et de forme toutes les nuits...)
Les limitations décrites ici motivent une représentation par complexification, décrite dans le chapitre suivant.
Les contraintes sur la taille de la scène, la mauvaise qualité des simplifications extrêmes et l'animation sont autant de limites aux méthodes de simplification générique. Cette approche est inapte à assurer le bon déroulement de la modélisation et du rendu de scènes animées avec de grandes variations d'échelle. Cela dépend de ce que l'on entend par "grandes variations d'échelle". Disons qu'à partir de certaines amplitudes dans les variations, la simplification échoue inexorablement.
Je précise ici que ce constat ne met pas ces méthodes hors course, loin de là.
Cela les assigne simplement à une marge de manuvre plus locale.
La simplification n'est pas la bonne approche pour résoudre le problème.
En revanche, il me paraît clair que la bonne approche, quelle qu'elle soit, devra utiliser la simplification pour arriver à ses fins.
Pour de nombreuses raisons, les algorithmes de simplification ne sont pas aptes à faire un rendu multi-échelle animé de scène complexe. Mais pourquoi ne pas retourner la critique ? Et si c'était la représentation utilisée pour décrire des scènes complexes qui n'était pas à la hauteur des algorithmes de simplification ?
Il est remarquable que les méthodes de simplification prennent toutes des données d'entrée de nature très simplistes. Dans la grande majorité des cas, les représentations utilisées sont des énumérations de points, éventuellement agrémentées d'une information de voisinage (graphe d'adjacence, grille). La plupart du temps, aucune information sémantique n'existe et on ne sait pas si on a affaire à un lapin ou à un tractopelle.
Pourquoi ne pas adopter une représentation plus complexe ?
2.1