3. Complexification

**Figure 3.1:** Ce chapitre propose une étude des différentes représentations procédurales multi-échelles existantes et de leurs applications.
$\begin{figure}\begin{center} \input{schema_comp.pstex_t}\end{center}\end{figure}$

Comme nous l'avons vu à la fin du chapitre précédent, la meilleure manière d'aborder la modélisation est l'affichage multi-échelle de scènes animées et d'introduire la multi-échelle le plus tôt possible dans le processus de création. C'est la conception même du modèle qui est multi-échelle (cf. figure 3.1).

Afin d'éviter une description explicite au niveau le plus fin, le modèle est décrit par une représentation complexe partant de sa forme la plus grossière et ajoutant de la précision : c'est la complexification.

La structure de ce chapitre est particulière. En effet, l'une des contributions de cette thèse est une analyse des besoins qu'engendre la complexification. Ce chapitre contient donc des parties d'état de l'art et des contributions. Voici précisément comment se déroule ce chapitre :

3.1 Modélisation procédurale multi-échelle

Dans cette section, nous essairons de mieux comprendre ce qu'est la modélisation procédurale, si présente dans ce mémoire. Après une (tentative de) définition basée sur celle donnée dans [EMP⁺98], son apport dans le cadre d'un rendu multi-échelle sera discuté.

3.1.1 Programme vs. structure de données

Reprise de nombreuses fois en synthèse d'image, la définition de ``modélisation procédurale'' est plutôt obscure. Néanmoins, il semble bien que l'élément essentiel soit la distinction entre programme et données.

3.1.1.1 Définition de référence

Dans le livre «Texturing & Modeling, A Procedural Approach» [EMP⁺98], David Ebert donne une définition de procédural : «the adjective procedural is used in Computer Sciences to distinguish entities that are described by program rather than by data structures». Cette définition oppose deux types d'informations : actives (le code) et passives (les données). La délimitation entre ces deux types d'informations est malheureusement très floue.

L'auteur de la précédente définition est d'ailleurs explicite quant à cette imprécision. Il prend notamment l'exemple d'une fonction faisant partie du programme. L'information la constituant est considérée comme étant de type actif. Mais ne peut-on pas considérer que les paramètres de cette fonction sont en fait une information de type passif? Il semble qu'ici encore, la vérité soit une question d'échelle : elle dépend de l'observation... Avant de m'essayer à mon tour à une définition, j'aimerais m'attarder un peu sur le contexte particulier dans lequel on se place : celui de la modélisation. Pour cela, il nous faut donc répondre aux questions suivantes : dans le cadre de la modélisation en synthèse d'images, qu'est-ce que le programme? Où sont les données?

3.1.1.2 Le programme

**Figure 3.2:** Durant le processus de création, un *programme* traite les idées du créateur ( les *données d'entrée*) et les transforme en pixels. On peut considérer que tout le système d'exploitation fait partie du programme, mais cela n'a que peu d'influence : on se focalise sur, le contexte, c'est à dire la *frontière* entre l'outil et les données entrées par l'utilisateur.
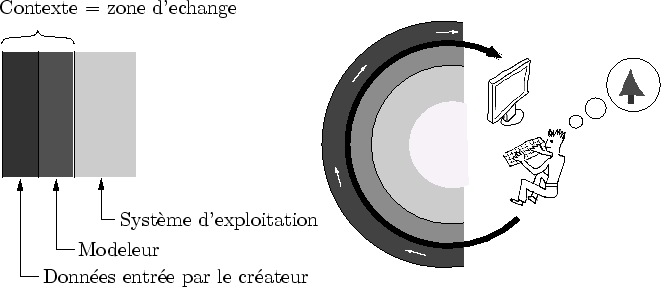$\begin{figure}\begin{center} \input{contexte.pstex_t}\end{center}\end{figure}$

Reprenons ici le processus de création : le créateur envoie des informations dans l'ordinateur qui sont transformées en pixels sur l'écran. Le programme, en synthèse d'images, est toute l'information qui décrit ces transformations. Très concrètement, c'est le code des programmes de modélisation et d'affichage ou plus généralement, toute information décrivant ces capacités de traitement de l'information (cf. figure 3.2).

3.1.1.3 Les données d'entrée

les données d'entrée sont, comme leur nom l'indique, données au programme par le créateur dans la phase de modélisation. Elles sont l'information imprévisible de la modélisation. Elles sont donc entièrement représentées par les actions physiques qu'opère le créateur devant son poste : bouton X, clic droit... On pourrait même remonter encore et déclarer qu'elles sont représentées dans la tête du créateur, mais elle est difficilement accessible ici... La représentation qui nous intéresse est celle du qui est retenue par le programme au moyen d'un langage descriptif.

Le langage descriptif est la grammaire utilisée pour représenter les données d'entrée dans le programme. Le choix de ce langage est d'une importance capitale. Par exemple, un modeleur peut mémoriser les opérations effectuées grâce à un maillage. Dans ce cas, chaque opération est oubliée et seul le résultat (le maillage) est stocké. Dans d'autres cas, ce sont les opérations qui sont stockées et la forme ne prend de sens que comme la succession d'application de ces opérations à une forme initiale. Il devient alors possible de remonter l'historique de la création et éventuellement faire des modifications ``dans le passé'' (comme le permet par exemple Maya avec son Dependency Graph [Ali03]).

3.1.2 Modélisation procédurale : définition

On peut donc opposer deux types d'informations : les données (le modèle 3D) et le programme (le modeleur). Une fois ce contexte situé, nous voila maintenant mieux préparés pour une nième définition de la modélisation procédurale.

3.1.2.1 Complexité du langage descriptif

Dans l'exemple précédent, on distingue différentes potentialités des langages descriptifs : un maillage permet moins de chose que la liste de toute les opérations effectuées par le créateur. Ceci n'est finalement que justice car mémoriser toutes les opérations effectuées par le créateur nécessite un langage complexe : il faut pouvoir y stocker tous les types d'opérations, leur domaine d'application, la date...

Définition : la complexité d'un langage descriptif est la taille de sa sémantique relativement à celle du programme qui l'utilise.

L'intelligence est assimilable à la prise d'initiative, l'indépendance. Par exemple, comment dessiner une forme représentée par un maillage? Il faut extraire et afficher tous les triangles un par un et les envoyer à la carte graphique. Un autre langage descriptif pourrait faire preuve de plus de finesse et intégrer dans sa représentation la façon dont elle s'affiche. Le programme principal n'aurait plus qu'à demander à une forme décrite avec ce langage de s'afficher, sans s'occuper des détails de l'opération. La complexité d'un langage descriptif est donc similaire à la concision de l'échange entre programme et donnée. Cette concision cache des processus complexes réalisés de façon relativement autonome par les données d'entrée.

3.1.2.2 Modélisation procédurale

Définition : une modélisation est dite procédurale lorsque la complexité du langage descriptif est grande.

Remarquons d'emblée que c'est une définition nuancée : plus la complexité du langage descriptif est grande, plus la modélisation est procédurale. L'idée intuitive, derrière cette définition, est de donner plus de pouvoir aux données d'entrée, plus d'expressivité. Ceci est à mon avis essentiel puisque ces données d'entrée sont les représentantes de notre intelligence au sein du programme!

Je suis conscient du manque de formalisme que l'on peut reprocher à cette définition, notamment dans l'utilisation du mot ``sémantique'' utilisé dans la définition de la compléxité. J'espère néanmoins avoir donner l'idée principale : rendre le modèle plus intelligent. Cette intelligence est absolument nécessaire dans le cadre de la multi-échelle où un modèle n'est plus une simple ``statue'', mais une forme en perpétuel mouvement, transformée d'une part par des méthodes d'animation, mais aussi par les mouvements de l'observateur.

3.1.3 Modélisation par complexification

Quels liens unissent la multi-échelle et la modélisation procédurale ? Est-ce que la modélisation procédurale n'est qu'une approche parmi d'autres pour aborder le problème des scènes observées avec de grandes variations d'échelle? Nous allons voir ici que ces deux concepts sont en fait inséparables. La problématique de la multi-échelle, devant l'échec de la simplification, mène naturellement à la modélisation procédurale. La méthode résultante, la modélisation procédurale multi-échelle, est nommée complexification.

3.1.3.1 Plus de souplesse

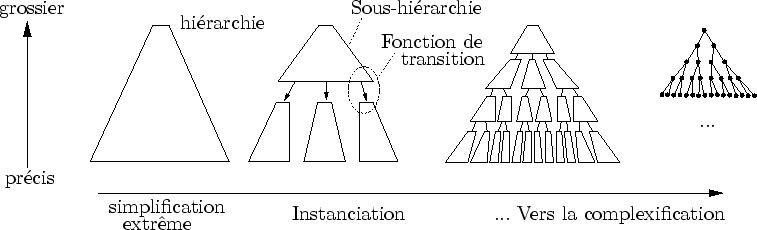
Nous avons vu dans le chapitre 2 qu'il était impossible d'espérer trouver des solutions aux problèmes posés par une méthode de simplification. Mais rien n'empêche de compliquer un peu le langage descriptif d'un modèle et de permettre que celui-ci englobe plusieurs sous-modèles. Ainsi, au lieu d'un seul modèle simplifié sur une grande plage d'échelle, plusieurs sous-modèles sont simplifié localement (cf. figure 3.3). On peut alors choisir des représentations et les algorithmes de simplification les plus adaptés à chaque sous-modèle. Notons que cette approche permet d'afficher plusieurs fois le même objet, puisque celui-ci n'est plus noyé dans une immense simplification : cette technique couramment utilisée se nomme instanciation [EMP⁺98]. Du coup, les problèmes de coût mémoire et de simplification extrême sont moins limitants.

Mais comment le créateur fait pour permettre au modèle de passer d'un sous-modèle à l'autre quand l'observateur se rapproche ? Supposons que l'on dispose d'un modèle de forêt observable de

ainsi que d'un modèle d'arbre observable de

. Sans même considérer des critères perceptuels complexes, le problème consistant à enrichir un modèle n'a rien d'évident. En effet, le modèle de la forêt peut très bien faire abstraction de l'individu et n'avoir alors que peu d'informations sur la manière dont un arbre va la remplacer. La solution consiste à décrire des fonctions de transition permettant de passer d'un modèle à l'autre et d'assurer le lien entre deux hiérarchies distinctes (cf. figure 3.3).

**Figure 3.3:** D'un modèle brutalement simplifié vers une représentation par complexification, la démarche est très naturelle. Le découpage et la réduction des plages de changement d'échelle permettent d'utiliser *différentes représentations adaptées* et de réduire les problèmes inhérents à la simplification.
$\begin{figure}\begin{center} \input{simp2comp.pstex_t}\end{center}\end{figure}$

3.1.3.2 Fonctions de transition

Ces fonctions de transition ont pour but de briser la lourde hiérarchie des niveaux de détail précalculés. Ainsi, elles doivent être très flexibles et ne pas reposer sur de grandes quantités d'informations. Pour le passage des forêts aux arbres, on peut imaginer une fonction qui va repérer, dans le modèle de la forêt, la place et l'espèce des arbres qui apparaissent.

Cette information peut être codée au sein de la forêt, mais de façon très concise. En tout cas, il est hors de question de décrire, dans le modèle de la forêt, chaque arbre entièrement et dans toute sa précision. On retomberait alors dans une représentation au coût mémoire exorbitant en ``recollant'' les sous-hiérarchies de chaque sous-modèle entre elles. Par contre, il est envisageable de stocker la place de chaque arbre de la forêt ainsi que d'éventuels paramètres (sa taille, son espèce, le nombre de branches...). Les fonctions de transitions consistent en fait en un paramétrage des modèles précis par le modèle grossier. Le modèle, lors d'un passage à un niveau plus précis, ne représente plus la forme brute, mais les paramètres qui vont permettre de l'afficher. On est bien en présence de modélisation procédurale.

3.1.3.3 Une description complexe mais dynamique

Le créateur, à cause des contraintes inhérentes à la simplification, est amené à représenter un modèle par plusieurs sous-modèles reliés entre eux par des fonctions de transition. D'une part, il ne manquera pas de remarquer que celles-ci sont difficiles à réaliser. En effet, il devra sans doute sophistiquer un peu le langage descriptif du modèle : celui-ci doit maintenant représenter non seulement des formes visuelles, mais aussi les fonctions permettant de les paramétrer. D'autre part, le créateur regrettera d'avoir été contraint à quitter les méthodes de simplification. En effet, celles-ci permettent de passer automatiquement d'une précision à l'autre. Désormais, ce passage est manuel et le bon déroulement des fonctions de transition est à sa seule et unique charge.

Néanmoins, notre créateur remarquera aussi que l'utilisation de fonctions de transition a décidément plusieurs aspects très positifs. Tout d'abord, elles répondent à leurs objectifs initiaux : elles réduisent les coûts mémoire et permettent des simplifications locales de bonne qualité. De plus, le paramétrage des sous-modèles, nécessaire aux fonctions de transition, peut être utilisé à d'autres fins. Notamment, ces nouveaux degrés de liberté permettent d'animer le modèle. Par exemple, revenons aux forêts et supposons que le modèle d'arbre dont on dispose peut changer de taille. Cette caractéristique, initialement prévue pour assurer une population d'arbres de taille variée, peut aussi servir à faire pousser les arbres au cours du temps.

3.1.3.4 Vers la complexification

La possibilité de faire pousser des arbres est certes une nouveauté en comparaison avec les méthodes de simplification pures qui permettent très difficilement l'animation. En revanche, cela est insuffisant pour rendre le mouvement des arbres sous le vent, par exemple. Du coup, afin de relaxer encore le modèle et d'y ajouter plus de degrés de liberté, notre créateur téméraire ajoutera des fonctions de transitions un peu partout. Il réduira en conséquence les phases de simplification et augmentera les possibilités d'animation (cf. figure 3.3). Ce faisant, il modélisera d'une façon bien particulière. Il commencera par la forêt vue de très loin et rajoutera des fonctions de transitions enrichissant progressivement la forme pour la rendre à chaque fois plus précise. Il pratiquera la modélisation par complexification.

Définition : La modélisation par complexification est une description d'un modèle par un ensemble de fonctions décrites dans un langage descriptif procédural (i.e. complexe). Ces fonctions ajoutent localement de la précision à une forme initiale grossière. Lors d'un affichage, elles sont rejouées jusqu'à satisfaire les critères d'observation (précision, visibilité...).

Au premier abord, complexification semble prometteuse. Mais il y a bien sûr beaucoup de problèmes à résoudre. Tout d'abord, comme nous l'avons déjà vu en 2.2.4, la simplification ne doit pas être mise de côté. En revanche, son utilisation, dans le cadre d'une application avec de grandes variations d'échelle, doit rester locale. Ensuite, la complexification nie l'automatisme ainsi que l'universalité et pousse vers des algorithmes toujours plus nombreux et spécialisés.

Historiquement, les premiers modèles par complexification sont les objets fractales qui sont étudiés dans la prochaine section. Plus récemment, quelques travaux assez récents utilisent la complexification afin de modéliser des phénomènes précis, dans des conditions d'observations particulières. Ils seront étudiés dans la section 3.3.

3.2 Fractales

Les fractales sont très polémiques en synthèse d'images : elles ont suscité beaucoup de critiques et leur utilité a été sévèrement remise en cause. De notre point de vue, elles sont pourtant extrêmement intéressantes : ce sont les premiers objets modélisés par complexification.

Nous commencerons cette section par une vue d'ensemble des fractales. Nous décrirons ensuite les méthodes utilisées pour accélérer le rendu d'objet fractal. Nos terminerons par la descriptions du ``Platonic World''.

3.2.1 Vue d'ensemble

Benoît Mandelbrot a découvert les objets fractales : des «objets infiniment complexes et autosimilaires à différents niveaux». Cette définition, proposée par Mandelbrot lui-même, ne le satisfait pas entièrement [Man75]. D'autres définitions existent, mais finalement, comme tant d'autres termes, la nature précise du mot ``fractale'' nous a un peu échappé. Entre considération esthétique et rigueur mathématique, que sont réellement ces objets? Quelle est leur utilité?

3.2.1.1 Un luxe

**Figure 3.4:** Les fractales ont décidément quelque chose d'intrigant. Lorsqu'on s'en approche ou s'en éloigne, l'animation engendrée est d'un effet très curieux. C'est un peu comme si notre cerveau pressentait la simplicité de la définition mais se laisser pourtant submergé par une apparente complexité.
$\begin{figure}\begin{center} \input{showfrac.pstex_t}\end{center}\end{figure}$

La visualisation fractale a eu son heure de gloire et la voilà maintenant réduite à remplir les fonds d'écran. À un curieux engouement esthétique a succédé un réel désintéressement scientifique. Les fractales ont néanmoins trouvé des applications en statistique, en compression et en traitement du signal [HRSV01].

Il n'en reste pas moins l'intérêt esthétique qu'elles suscitent (cf. figure 3.4). Les images générées ont quelque chose d'un peu mystique au point que nombreux sont ceux qui déclaraient que l'univers était fractal. Dernièrement, certains logiciels ont permis de zoomer sur des fractales en temps-réel [xao,eas]. Ces logiciels, très spécialisés, permettent de très grandes variations d'échelle dont la limitation est la précision numérique des flottants. Naviguer dans une fractale est une expérience très particulière : la complexité d'un univers engendré par une simple équation peut être étonnante et les ``paysages'' auto-similaires (et pourtant subtilement différents) sont très attrayants, presque hypnotiques.

3.2.1.2 Un bon rapport qualité prix

Chacun définit le mot fractale de son propre point de vue. Un mathématicien (mais pas tous) dira que c'est un objet dont la dimension de Hausdorff est supérieure à sa dimension topologique. Un artiste dira que c'est une jolie image répétitive à différentes échelles... Définir de tels objets est délicat. Pourtant, il existe une caractéristique commune à toutes les fractales : la complexité de l'information générée. Lorsqu'on la visualise, la complexité d'une fractale paraît être bien plus grande que la complexité de sa définition. En d'autres termes, une fractale est une fonction mathématique simple dont l'observation (i.e. la visualisation) est disproportionnellement complexe. Un bon rapport $\frac{qualit\acute{e}}{prix}$ en quelque sorte...

Du point de vue de la multi-échelle, cette abondante complexité est très séduisante : les fractales nous offrent des univers qui nous apparaissent comme infiniment complexes. Ici, il n'est plus besoin de décrire le modèle à son niveau le plus fin pour le simplifier (cf. chapitre 2), avec tous les problèmes que cela engendre. Une simple formule décrit implicitement la scène à toutes les précisions possibles. En effet, le calcul d'une fractale est généralement itératif et ajoute à chaque pas un peu plus de précision : il suffit donc d'arrêter l'itération à une certaine valeur pour obtenir la précision correspondante.

**Figure 3.5:** La construction de certaines fractales peut être vue comme un ajout successif de précision.
$\begin{figure}\begin{center} \input{snowflake.pstex_t}\end{center}\end{figure}$

3.2.1.3 Quelques faiblesses

Synthétiser des mondes sur lesquels on n'a aucun contrôle est un exercice lassant. De plus, d'un point de vue scientifique, l'Homme doit plier l'informatique à ses désirs, et non la laisser générer ce que bon lui semble. En fait, la modélisation d'objet fractal et parfois très hasardeuse : il s'agit d'essayer de comprendre ce qui se passe lorsque l'ordinateur devient imprévisible. D'ailleurs, les liens très forts entre les sciences du chaos, des systèmes déterministes et des fractales ne sont pas anodins. Pourtant, malgré leur irréalisme et leur aspect incontrôlable, les objets fractales ont soulevé de nombreux problèmes très intéressants.

3.2.2 Calculabilité

Les fractales sont les premiers univers virtuels dans lesquels on peut zoomer infiniment. Pour la première fois, ce n'est plus le modèle qui est limitant dans la navigation multi-échelle, mais l'algorithme de rendu. Voyons comment celui-ci a été modifié pour permettre un rendu efficace de fractale.

3.2.2.1 Précision itérative

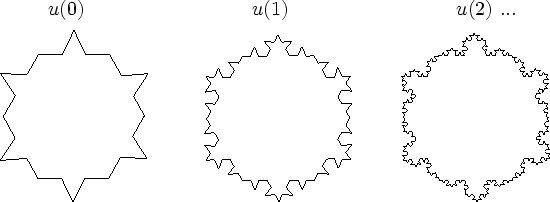
Les fractales sont infiniment précises. Les méthodes utilisées pour visualiser une fractale consistent à complexifier (amplifier) l'information jusqu'à ce que la précision devienne suffisante. La représentation d'une fractale n'est donc pas la forme proprement dite, mais la façon dont elle se construit. Cette propriété est absolument prépondérante lors de son évaluation (i.e. dérivation). De ce point de vue, une fractale n'est ni plus ni moins que la limite d'une suite convergente (cf. figure 3.5).

Les suites utilisées sont récursives, ce qui permet de déduire un niveau de détail du pas de calcul antérieur. La représentation sous forme de suites récursives des formes tridimensionnelles est providentielle dans le cadre de la multi-échelle. En effet, l'observateur peut se rapprocher, c'est-à-dire rajouter des itérations, ou bien reculer, c'est-à-dire revenir aux itérations précédentes (que l'on a gardé en mémoire). De cette façon, la forme n'est jamais décrite explicitement au niveau le plus fin : seule une évaluation plus ou moins précise permet d'engendrer la forme adéquate.

3.2.2.2 Évaluation paresseuse

La représentation sous forme de suite convergente permet donc de ne calculer que la précision nécessaire à l'observation. En effet, il suffit de trouver le bon

tel que

satisfasse la précision requise par l'observateur (cf. figure 3.5). Mais les critères d'arrêt, dans l'espace tridimensionnel, ne sont pas aussi simples qu'un seuil entier jusqu'où la fractale est uniformément calculée. En effet, les formes visibles n'ont pas la même précision dans une même image donnée (cf. figure 1.1). De plus, certaines parties ne sont pas visibles pour diverses raisons : hors-champ, occultées...

Il est donc nécessaire de réaliser une évaluation paresseuse qui calcule la fonction fractale le moins possible de façon à ne générer que l'information utile à une observation^3.1. Une évaluation paresseuse consiste à ne calculer l'information que là où elle est pertinente (cf. John C. Hart dans [EMP⁺98]). De cette façon, l'algorithme de rendu devient output sensitive : son coût dépend de la complexité de l'observation (entre autres : nombre de pixels sur l'écran) et non de la complexité de la fractale^3.2.

La grande majorité des fonctions fractales est bidimensionnelles. En conséquence, les évaluations paresseuses mises en $\oe$ uvre sont généralement très simples. D'une part, la précision est uniforme (critère d'arrêt global). D'autre part, la visibilité consiste juste à ne pas engendrer ce qui est en dehors de l'écran (pas d'occultation). En trois dimensions, ces problèmes sont plus délicats. Les problèmes de précision [Red97] et de visibilité [Dur99] ont été essentiellement étudiés dans le cadre d'approche par simplification.

3.2.2.3 Cohérence temporelle

La nature très continue de la majorité des observations faites par l'Homme permet d'optimiser les calculs en utilisant la cohérence temporelle. En effet, la quasi-totalité des méthodes de visualisation impose des mouvements de caméra suffisamment lents pour que l'image générée à un pas de temps ressemble à celle du pas du temps précédent. Il est donc possible d'accélérer le calcul d'une image en se basant sur sa similarité avec l'image précédente. C'est une sorte d'évaluation paresseuse temporelle.

L'utilisation de la cohérence temporelle est un concept très général utilisé dans plusieurs domaines et pour de nombreuses applications. Néanmoins, son utilisation est relativement rare dans le cadre de la modélisation fractale. En effet, l'optimisation par cohérence temporelle nécessite la connaissance de la forme visible au pas de temps précédent, puisque c'est sur ces données que l'optimisation est fondée. Or, une fractale est généralement générée à la volée, rendant ainsi très volatile les informations qui la décrivent.

En effet, lorsqu'une scène est décrite par des fonctions de construction, sa définition est implicite. Sa description explicite (géométrie, matériaux) n'existe souvent que lors d'une observation (d'une évaluation). Parfois, elle n'a même aucune existence dans la mémoire de l'ordinateur, mais n'apparaît que de façon très fugace au sein même du processeur (dans la la pile d'appels par exemple).

Il faut donc faire un effort particulier pour garder la description explicite en mémoire. Cet effort consiste généralement à coder une structure de donnée qui stocke et rend accessible cette information ancienne (c'est notamment le cas de XaoS [xao]). Remarquons que la problématique est subtilement différente pour les algorithmes utilisant des descriptions explicites. En effet, ceux-ci offrent la possibilité de modifier l'information existante, ce qui est déjà une forme d'optimisation par cohérence temporelle.

3.2.3 Modélisation fractale et langage descriptif

La modélisation fractale est généralement un acte délicat. Trouver des méthodes simples de construction dont peuvent résulter des observations très complexes n'est pas chose aisée. C'est en tout cas moins intuitif que de décrire une forme à une précision donnée^3.3. La plupart du temps, c'est une idée qui jaillit sans prévenir, ou un coup de chance, voire même un ``bogue''. Plutôt qu'un acte de création, les fractales semblent être issues du hasard. Pourtant, certains outils proposent un cadre formel permettant leur modélisation.

3.2.3.1 Classement

Le système de réécriture des L-systèmes consiste, pour un certaine type de règle, à rajouter de l'information. L'idée d'ajouter de l'information est bien adapté à la multi-échelle : on va ajouter de la précision en fonction de la multi-échelle. Cette similitude entre croissance et précision, mise en évidence dans [Coe00,Smi84], fait des L-systèmes un langage bien adapté à une description multi-échelle.

3.2.3.2 Présentation des L-systèmes

Créer une fractale revient à trouver des fonctions simples dont la composition donnera lieu à des observations intéressantes. Très vite, les L-systèmes (et les grammaires en générale) se sont avérées pratiques pour coder ce genre de construction. En effet, lorsqu'une production crée de nouveaux symboles, ceux-ci peuvent soit être interprétés (observés), soit engendrer de nouveaux symboles (par l'application d'autres règles).

Plus généralement, les langages descriptifs utilisés pour décrire des fractales ne sont ni plus ni moins que de petits langages de programmation. «Pourquoi petit?». De nombreuses contraintes pèsent sur les langages descriptifs de fractales :

Ces considérations évoquent un curieux équilibre entre créativité et expressivité^3.4. Les L-systèmes ne seraient-il pas trop contraint pour la modélisation de scènes tridimensionnelles ? Ici, les résultats parlent d'eux même : dans un cadre non multi-échelle, la variété et la richesse des modèles crées sont époustouflantes [PHM99,CXGS02].

De plus, certains travaux s'attachent à donner aux L-systèmes le plus d'expressivité possible :

3.2.4 Platonic World

Le Platonic World [PGF01] consiste en une formalisation de la modélisation par complexification. Le langage descriptif utilisé est un L-système. Ce travail étant étroitement lié au mien, il est maintenant décrit et discuté.

3.2.4.1 Concept

**Figure 3.6:** L'évaluation d'un L-système est ici représentée par un arbre de dérivation (éventuellement cyclique). La chaîne de caractères d'un L-système peut être dérivée à l'infini, mais une observation correspond à une coupe de cet arbre.
$\begin{figure}\begin{center} \input{cut.pstex_t}\end{center}\end{figure}$

Le monde platonique est un monde où tout existe sous forme ``d'idée'' et où ces idées ne prennent une apparence palpable dans le mode réel que si elles sont observées. En langage informatique, cela signifie qu'il ne faut afficher que ce qui est visible à la bonne précision. Pour arriver à cela, les traditionnelles méthodes de visibilité sont appliquées. C'est la grande série des ``culling'' qui énumère tous les critères pour lesquels une forme visible doit être acceptée ou rejetée.

L'originalité de la méthode de Przemyslaw Prusinkiewicz et de Christophe Godin vient du fait que des graphes multi-échelles y sont représentés par des L-systèmes. Les objets modélisés avec Platonic World sont essentiellement des fractales. Un modèle d'arbre a aussi été écrit (à rapprocher avec [WP95,LCV03]), ce qui illustre le fait que le Platonic World n'est pas restreint aux objets auto-similaires à différentes échelles.

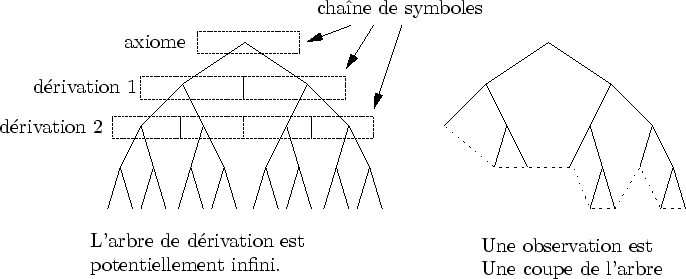
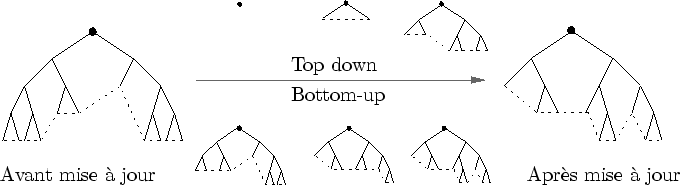
Du point de vue de la multi-échelle, c'est l'approche des fractales qui est retenue : un objet est représenté implicitement par les fonctions qui vont progressivement enrichir sa précision. Platonic World représente à ma connaissance la première formalisation du concept de Modélisation multi-échelle procédurale. L'échelle d'un objet est décrite comme une fonction de sa distance à la caméra. Des boîtes englobantes hiérarchiques sont utilisées pour déterminer si un objet est hors champs ou non. L'évaluation du L-système est représentée par un arbre potentiellement infini. Une observation y est caractérisée par une coupe de l'arbre. Une coupe d'un arbre est un sous-arbre comprenant la racine (cf. figure 3.6).

Dans Platonic World, Lorsque l'observation change, la forme change aussi. De quelle manière doit-on mettre à jour l'arbre qui la représente? Deux approches sont fondamentalement opposées :

D'un point de vue théorique, ces deux approches ont chacune leurs avantages et leurs inconvénients. Principalement, remarquons que la méthode Bottom-up, pour être efficace, implique une bonne cohérence temporelle lors d'une animation (du modèle lui-même ou de la caméra). Le choix de l'une ou l'autre des approches n'est donc pas évident et la question est à ma connaissance laissée en suspens.

**Figure 3.7:** Lors d'une mise à jour de la figure, deux approches s'opposent. La méthode *Top-down* commence par la racine et descend vers les feuilles. La méthode *Bottom-up* commence par les feuilles et remonte vers la racine (elle redescend cependant lorsque des détails sont ajoutés).
$\begin{figure}\begin{center} \input{topdown.pstex_t}\end{center}\end{figure}$

3.2.4.2 Discussion de l'implémentation actuelle

Les mondes générés avec Platonic World sont en deux dimensions. Même si la méthode reste conceptuellement la même en trois dimensions, certaines difficultés supplémentaires viennent se greffées aux problèmes.

Les mondes générés par le Platonic World ne sont pas animés. Encore une fois, cela ne changerait rien au concept originel. Cependant, la formalisation des parcours Top-down et Bottom-up n'a pas été pensée pour des objets animés. En effet, l'intérêt du parcours Bottom-up implique l'utilisation d'un modèle statique. Dans le cas d'objet animé à tous les niveaux de détail, le parcours Bottom-up serait impraticable. Nous voyons les parcours Top-down et Bottom-up comme deux méthodes parmi d'autres pour mettre à jour un modèle en fonction du temps et de la position de la caméra.

Le langage L-système est un langage simple, minimaliste. En un sens, il est au langage de programmation ce que les cartes graphiques sont au CPU : une version spécialisée, simple et rapide^3.5. Le système d'interprétation implémenté dans L-Studio est celui de la ``tortue'', correspondant à des push/pop de matrices en OpenGL. Un catalogue de formes tridimensionnelles est disponible pour l'affichage. Les fonctions d'interprétation et les formes disponibles sont implémentées dans le programme principal. L'ajout ou la modification de nouveaux éléments requiert une re-compilation de ce dernier, entravant ainsi gravement les possibilités d'extension. Il est souhaitable, dans un contexte algorithmique aussi délicat que la modélisation multi-échelle, d'avoir plus de marge de man $\oe$ uvre qu'un simple éventail d'objets aux repères tridimensionnels variables. Je défend dans ce manuscrit l'hypothèse selon laquelle les limitations drastiques des langages simples brident la créativité et contraignent le ``champ des possibles''.

3.3 Loi du cas particulier

Contrairement aux méthodes de simplification, la complexification ne se prête guère à la généralisation et à l'universalisation. Ainsi, les programmes adhérant à cette philosophie sont tous appliqués à des phénomènes très spécifiques : c'est la loi du cas particulier. Nous nous proposons ici d'énumérer ces travaux afin d'en extraire un besoin commun. L'énumération commencera par les travaux orientés modélisation. Ensuite, une partie sera réservée aux applications non-académiques. Enfin, nous nous intéresserons aux algorithmes plus orientés rendu temps-réel.

3.3.1 Travaux orientés vers modélisation

Avant de décrire les rares travaux permettant la description de formes tridimensionnelles du plus grossier au plus fin, le cas bidimensionnel est rapidement survolé. Seront ensuite analysés les langages de description, les interfaces graphiques et enfin les outils de modélisation par contraintes (CAO).

3.3.1.1 Deux dimensions

De nombreuses applications 2D utilisent des représentations procédurales. Par exemple, le très répandu format vectoriel (postcript) est un codage de l'image utilisant des fonctions plutôt qu'une grille de points. Ce codage est très utilisé en cartographie où les deux représentations sont en concurrence : matricielle versus vectorielle^3.6. De façon plus générale, une simple page HTML ou le moindre système de fenêtrage est une image procédurale. En deux dimensions, les représentations procédurales sont décidément bien implantées.

Les travaux multi-échelles sont plus rares. Par exemple, les textures de Perlin offrent la possibilité de garder une représentation procédurale [Per02,PV95]. Mises à part les approches fractales discutées dans la section 3.2, la modélisation multi-échelle 2D n'est en fait guère plus développée que la multi-échelle 3D. Il est bien sûr possible de réaliser des animations 2D multi-échelles avec la quasi-totalité des outils de modélisation. Mais aucun d'entre eux, à notre connaissance, n'est prévu pour cela.

3.3.1.2 Langage descriptif expressif

J'aimerais ici parler de Slithy [ZS03], une bibliothèque écrite Python permettant de réaliser des présentations similaire à ``Powerpoint''. En effet, cet outil peut tout à fait être analysé sous l'angle de la modélisation multi-échelle procédurale de scènes massivement animées. Il suffit pour s'en convaincre de voir les présentations qui l'utilisent.

Python permet une incroyable expressivité. Notamment, il est réflexif [Gra95], ce qui signifie que le type ``code python'' existe dans Python^3.7. Cette ``réflexivité'' est en quelque sorte le ``comble'' de la modélisation procédurale : le langage descriptif est aussi complexe que le langage de programmation.

3.3.1.3 Langages descriptifs tridimensionnels

Il est difficile de recenser les langages permettant une modélisation par complexification en trois dimensions. Non pas parce qu'ils sont peu nombreux, mais parce que tous les langages, dans une certaine mesure, le permettent. Voici donc un petit échantillon représentatif des travaux existants :

Les interfaces textuelles sont actuellement plus expressives que les interfaces graphiques. Entre autres, elles ne sont pas focalisées sur des cas particuliers. Bien entendu, cette permissivité est gagnée au prix d'un confort d'utilisation très médiocre. On peut considérer que l'interface graphique est le plus haut niveau d'abstraction que peut atteindre un langage de modélisation multi-échelle procédurale. Dans ce cas, quelques étapes restent encore à parcourir avant la réalisation de cet objectif.

3.3.1.4 Modélisation interactive

De récents travaux [BPF⁺03,KN02] proposent pour la première fois des interfaces graphiques permettant la modélisation multi-échelle de forme tridimensionnelle. Uniquement axés sur la modélisation, ces systèmes ont certains points communs :

Ces travaux pionniers en modélisation multi-échelle pourraient éventuellement se prolonger vers le rendu :

3.3.1.5 Entre simplification et complexification

Les surfaces de subdivision [Loo94] peuvent être vues comme des méthodes de complexification. Malheureusement, l'ajout de détails n'est souvent réalisé que dans un seul but : celui de lisser la forme. Même si d'autres schémas de subdivision existe, ils souffrent la plupart du temps d'un manque de contrôle certain : c'est le même schéma de subdivision qui est répété à l'infini.

D'autres techniques permettent d'ajouter des détails plus variés à un maillage [EDD⁺95] ou un volume [GLDH97]. Elles s'appuient sur des méthodes par ondelettes [SDS96] ou en sont conceptuellement proche. Ce codage permet un certain dynamisme dans l'affichage : on peut passer d'une représentation à l'autre de façon continue en rajoutant progressivement l'influence d'un coefficient.

Malheureusement, le langage descriptif utilisé est très simple. En effet, le choix très restreint d'une base de fonctions d'ondelette impose une discrétisation fine de l'espace. Il devient alors difficile de garder une information sémantique forte : on manipule des tableaux de coefficients. En pratique, toutes ces méthodes partent d'une information représentée à sa précision maximum qui est décomposée en ondelette. A notre connaissance, personne ne s'est intéressé à la génération procédurale de coefficients d'ondelette.

De même que pour la simplification, ces méthodes sont absolument nécessaires à la réalisation de scènes tridimensionnelles multi-échelles à un niveau local, mais elles s'adaptent mal, pour l'instant, à de très grandes variations d'échelle.

**Figure 3.8:** Quelques (magnifiques!) rendus réalisés avec Pandromeda. Après expérimentation du logiciel, il est clair que les temps de calcul de ses images sont bien loin du temps-réel.
$\begin{figure}\begin{center} \input{mojo.pstex_t}\end{center}\end{figure}$

3.3.2 Travaux non-académiques

De nombreux travaux sont réalisés en dehors du circuit académique. Obéissant à d'autres contraintes que ce dernier, peu d'informations sont disponibles. Il est néanmoins possible de déduire certaines propriétés par une simple observation. Voici donc une liste des produits dont j'ai connaissance agrémentée de quelques commentaires.

Les intervalles d'observation donnés sont approximatifs mais donnent une bonne estimation de ce que permet le modèle. Vous pourrez trouver plus d'informations sur le site très complet de VTerrain [vte].

3.3.2.1 Pandromeda [moj,MKM89]

Ken Musgrave est certainement l'un des plus fervents adeptes de la modélisation procédurale multi-échelle. Son travail sur Mojo Word en est l'indiscutable preuve (cf. figure 3.8). Mojo Word se distingue par des interfaces graphiques très soignées et bien pensées (ce qui n'a rien d'évident en modélisation procédurale). Les méthodes employées semblent être massivement orientées vers la génération procédurale de textures. Les temps de calcul sont assez lents (du moins, plus lent que ce que l'on pourrait espérer). Les résultats, moyennant un peu de patience, peuvent être vraiment spectaculaires. Cet outil a été conçu pour être très modulaire, près à accueillir de nouveaux plugins. Très paramétrable, Mojo Word est néanmoins spécialisé pour le rendu de vaste terrain. L'intervalle d'observation est assez large, permettant de zoomer de plusieurs kilomètres à quelques mètres. Dans l'ensemble, c'est un logiciel très prometteur orienté vers la modélisation procédurale multi-échelle.

3.3.2.2 Speedtree [spe], Blueberry3d [Wid], Gscape [gsc]

**Figure 3.9:** La végétation est un terrain de prédilection pour les méthodes de complexification. Ces images tirées de produits commerciaux en sont la preuve.
$\begin{figure}\begin{center} \input{ext_terrain.pstex_t}\end{center}\end{figure}$

Ces logiciels concurrents (cf. figure 3.9) proposent tous un rendu de végétation en temps-réel très convaincant. Ils sont basés sur une utilisation intensive de Billboards semi-transparents. Dans un certain intervalle d'observation, le problème de rendu de végétation semble être en grande partie résolu. Blueberry3d se distingue par un intervalle d'observation plus grand. Notamment, une vidéo montre un zoom impressionnant sur une forêt (de

3.3.2.3 XaoS [xao], EasyFractal [eas]

Xaos est un logiciel spécialisé dans le rendu de l'ensemble de Mandelbrot. C'est à mon sens un petit bijou algorithmique et une référence en la matière. L'algorithme est basé sur une cohérence temporelle forte assurée par une méthode bottom-up pour le rendu de l'image suivante. EasyFractal semble faire plus ou moins la même chose, mais je n'ai pas pu l'expérimenter.

3.3.2.4 En vrac

**Figure 3.10:** Quelques images du jeu *Black and white* dans lequel vous êtes un ``Dieu multi-échelle''.
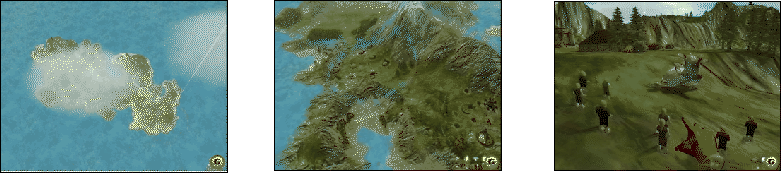$\begin{figure}\begin{center} \input{bw.pstex_t}\end{center}\end{figure}$

Le jeu Black and White [Stu01] propose de devenir Dieu. Ce dernier, comme tout Dieu qui se respecte, peut tout voir et tout faire. En conséquence, un travail exceptionnel a été réalisé pour permettre de grandes variations d'échelle (cf. figure 3.10).

Virtual Skipper [vsk] est un jeu de course de bateau dont le rendu de l'océan, multi-échelle et procédurale, et impressionnant.

Celestia [cel] est un rendu de l'Univers (notre univers). Esthétiquement, c'est sans prétention. Par contre, c'est du vrai temps-réel avec des zooms de la galaxie vers le système solaire et la Terre (vue satellite). C'est la preuve que la multi-échelle a sa place dans les logiciels pédagogiques.

Descensor [des] est un logiciel qui propose de générer des villes procéduralement. La distance d'observation varie de

. Lors d'un zoom arrière, des imposteurs simplifient la géométrie. Très convaincant dans le discours, ce logiciel passe assez mal le cap de la démonstration.

3.3.2.5 Bilan

Tous ces produits appuient la loi du ``cas particulier''. En effet, aucun logiciel ne prétend faire un rendu multi-échelle générique. Tous sont spécialisés (villes, fractales, planète). Chaque modèle est observable dans des intervalles bien délimités. La politique de Mojo Word sur les plugins est une façon de proposer un cadre commun à l'expression des nouveaux résultats en modélisation procédurale. En effet, aucun format de fichier n'est actuellement capable de représenter un large éventail de données multi-échelles. C'est une sorte de crise d'identité : tous ces travaux ont besoin d'une bannière commune pour aller plus loin dans la variété et l'amplitude des variations d'échelle.

3.3.3 Travaux académiques

La recherche en synthèse d'image a récemment engendré une série de travaux s'appuyant sur la modélisation procédurale multi-échelle. Puissance des machines ou maturité des recherches, le temps-réel est désormais accessible, même avec de grandes variations d'échelle. C'est sans doute l'un des tournants historiques de la multi-échelle : les limitations semblent maintenant venir de l'algorithmique plus que du matériel. L'avenir s'annonce radieux...

3.3.3.1 Arbres

Les arbres et les forêts sont les travaux les plus nombreux. Weber [WP95] est sans doute le premier à proposer des arbres multi-échelles. Alexandre Meyer utilise des fonctions d'éclairage procédurales et multi-échelle [MN00], puis une représentation à base d'image [MNP01] pour un rendu plus efficace. Xavier Baele [Bae03] utilise la programmabilité du vertex-engine pour générer les branches à la bonne précision. Un soin particulier est apporté aux transitions, réalisées par un fondu enchaîné des modèles 3D dans l'espace image. Thomas Di Giacomo [GCF01] permet une animation d'arbre multi-échelle basculant entre méthodes réactives et prévisibles selon la position de l'observateur. Marc Stamminger [SD01] utilise un rendu par point (avec lequel il modélise aussi d'autres types d'objets procéduraux). Olivier Deussen affiche des végétations complexes [DCSD02], mais on est plus ici dans une optique de simplification.

3.3.3.2 Prairie

Nous avons réalisé, au début de ma thèse, un programme permettant le rendu temps-réel de prairie animée. L'approche est multi-échelle et procédurale, aussi bien dans la forme que dans l'animation : des imposteurs se transforment en géométrie pendant que des primitives de vent balayent le terrain. A la première version [PC01] a succédé une seconde mouture, améliorant très sensiblement les résultats [GPR⁺03]. Programme fondateur de cette thèse, il est décrit précisément dans le chapitre suivant.

[BLH02] propose un rendu de prairie à base de points. Je pense que le rendu par points est utile dans le cas de formes pour lesquelles l'information de voisinage est très chaotique (comme les feuilles d'un buisson par exemple). L'aspect longiligne d'un brin d'herbe me semble donc mal se prêter à ce genre de représentation.

3.3.3.3 Terrain

Les rendus de terrain ont tout d'abord été traités par des méthodes de simplification [LRC⁺02]. Mais de nombreuses applications ne tirent aucun profit à la connaissance du terrain au niveau le plus fin. De plus, le dynamisme de la représentation nécessaire au changement rapide de point de vue a orienté certaines méthodes vers des techniques de complexification [SD01,MKM89].

3.3.3.4 Océan

Certains travaux proposent un affichage temps-réel des surfaces procédurales. Ils sont très remarquables car la modélisation procédurale est usuellement utilisée pour modéliser des formes structurées de façon hiérarchique. Damien Hinsinger modélise un océan en temps-réel [HNC02]. La projection inverse de la grille de l'écran sur l'océan et les fonctions d'animation multi-échelles adaptative participent à rendre ce travail très original. C'est à mon goût l'un des plus beaux exemples de réalisation procédurale multi-échelle.

3.3.3.5 Ville

Longtemps abordées par les techniques de simplification, les villes de Yoah Parish sont entièrement procédurales. Elles profitent de la sémantique forte inhérente à tout son modèle procédurale pour faire des approximations géométriques intelligentes. Toujours dans le milieu urbain, certains travaux proposent des solutions au problème posé par la modélisation de foules multi-échelles. Les approches retenues sont actuellement très axées sur la simplification [TLC02,WS02].

3.3.3.6 Poils et cheveux

Les poils et les chevelures sont des structures très réfractaires aux méthodes de simplification (forme complexe et très animée). Jerom Lengyel [LPFH01] permet le rendu (et l'animation) de poils courts en temps-réel par volumes approximés par tranche (une approche simple et redoutablement efficace). La détection de contour permet l'ajout de la précision sur la silhouette, là où notre $\oe$ il en requiert le plus. Florence Bertails [BKCN03] modélise, anime et affiche des mèches de cheveux multi-échelles. La méthode d'animation utilisée est remarquable puisqu'elle adapte sa complexité à la précision requise par l'observation (de loin ou au repos, seules quelques mèches sont prises en compte).

3.3.4 Des besoins similaires

Le petit nombre de travaux cités ici et leur caractère très spécifique à une application particulière montrent la pauvreté, voire l'inexistence, des outils génériques de modélisation par complexification. Il est donc nécessaire d'envisager des outils plus évolués. A la lumière des travaux existants, recensons les principaux besoins afin de tracer les grandes lignes d'un modeleur multi-échelle procédural.

3.3.4.1 Outils génériques existants

Le but de tous ces programmes est toujours le même : n'afficher que ce que l'on voit. Ce but se décompose en sous-objectifs ; c'est la série des cullings : back-face culling, view frustrum culling, precision culling, occultation culling, ... De nombreux graphes de scène proposent des algorithmes pour répondre à toutes ces façons de réduire la forme visible à l'essentiel [Inv,Per,Jav,Opeb,Opec,Opea,Giz,Ren,Wor]. Quelques fonctionnalités multi-échelles sont disponibles comme des algorithmes de rendu de terrain multi-échelle ou la gestion de hiérarchie de niveaux de détail statique. Néanmoins, tous ces outils sont pensés pour la représentation de scènes connues à l'avance et supportent mal la génération procédurale à la volée.

3.3.4.2 Précision et visibilité

La complexification entraîne notamment l'utilisation intensive de fonctions de transition. Implémenter une transition est le genre de code qu'il est possible d'écrire en quelques minutes de façon très naïve, mais qui prend beaucoup plus de temps si l'on désire la contrôler subtilement. Les transitions utilisent notamment la précision, notion vague et toujours délicate à coder de façon générique.

La quasi-totalité des algorithmes de visibilité [MKM89] est basée sur des précalculs lourds et elle est donc inadapté à la modélisation par complexification. Pour bénéficier d'un algorithme de suppression des faces occultées, la seule solution consiste actuellement à le coder soi-même pour chaque objet modélisé (comme dans [SD01]). En conséquence, il serait souhaitable mettre à disposition un système de visibilité générique applicable aux méthodes procédurales. Les autre ``culling'' (back-face, view frustrum) posent moins de difficultés techniques mais bénéficieraient tout autant d'une implémentation générique.

3.3.4.3 Modélisation

Le rendu de scènes procédurales multi-échelles produit un flux d'information soutenu et très volatile, s'adaptant au moindre mouvement de la caméra. Ce flux doit être canalisé lors du rendu (précision, visibilité) afin de garder des performances correctes. Remarquons que le temps d'affichage d'un objet est essentiel à sa modélisation. En effet, la répercussion immédiate des modifications faites par le créateur est garante d'un meilleur confort de modélisation^3.8.

Notamment, l'utilisation de langages descriptifs complexes doit être accompagnée d'outils adéquats. En effet, plus un langage est expressif, plus il est possible de commettre des erreurs. Par exemple, de nombreux langages nécessitent même des débogueurs tant ces erreurs peuvent être complexes et difficilement repérables. En synthèse d'images, les formes modélisées sont affichées sur l'écran, ce qui est parfois suffisant pour déterminer l'origine d'une erreur. De plus, certaines modélisations procédurales utilisent des langages très répandus (Python, C++) et bénéficient alors d'environnements existants. Néanmoins, ceux-ci sont mal adaptés à la complexification et à son flux d'information dense et versatile.

Des outils d'aide à la modélisation seraient d'un grand secours ici. Le flux d'information peut être visualisé de façons très diverses. De nombreux travaux montrent les niveaux de détail utilisés par de fausses couleurs. De même, un rendu de la scène vue par un deuxième observateur s'avère souvent très utile pour mieux observer le comportement de certaines transitions. De plus, la complexification implique une connaissance forte sur les objets manipulés. Cette connaissance peut être mise à profit pour créer des micro-environnements de développement parfaitement adaptés au type de l'objet observé.

3.3.4.4 Plus de richesse

Les travaux cités en 3.3.3 bénéficieraient tous plus ou moins de l'utilisation d'un outil factorisant les problèmes communs (précision, visibilité, cohérence temporelle, persistance, environnement de modélisation...). Mais ils bénéficieraient aussi de leur simple mise en commun au sein d'une même scène tridimensionnelle. En effet, les scènes que l'on pourrait réaliser en rassemblant les travaux existants laissent rêveur : des forêts, des prairies, des montagnes, des océans, des villes... En pratique, une telle mise en commun est délicate. Certes, les programmes sont quasiment tous écrits en C++, mais la mise en commun de deux programmes dont les architectures sont radicalement différentes peut être un véritable calvaire.

Ce problème délicat peut être allégé par l'utilisation d'un format commun. Par exemple, il est facile de réunir deux modèles VRML dans un même modeleur pouvant lire ce format. Malheureusement, aucun format standard de modèles 3D ne permet aujourd'hui de coder aisément des représentations procédurales. Nous voilà donc confrontés à une requête essentielle : un langage capable de décrire des modèles procéduraux multi-échelles. Malheureusement, les formats disponibles actuellement sont soit peu expressifs (comme les L-système), soit inefficaces (comme Python). Il semble bien difficile de se passer de l'expressivité et de la puissance de langage tel que le C++.

3.3.4.5 Mise en commun des intervalles d'observation

Le format commun décrit plus haut permettrait non seulement de rassembler différents modèles à la même échelle, mais il permettrait aussi une mise en commun multi-échelle. On pourrait alors, par exemple, utiliser un modèle de planète et le connecter à des modèles de prairie, de forêt et d'océan. De cette façon, on cumulerait les intervalles de validité des sous-modèles. Il deviendrait possible de créer petit à petit des modèles couvrant des intervalles d'observation gigantesques et offrant, pour la première fois, de grandes variations d'échelle et une grande variété au sein de ces différentes échelles. En effet, les seuls modèles permettant actuellement de grandes variations d'échelle sont les fractales, très monotones dans leur différentes résolutions.

Cette mise en commun multi-échelle n'est pas aussi évidente qu'une mise en commun ``mono-échelle''. En effet, les fonctions de transition, évoquées dans la section 3.1 , ne sont pas des formules magiques et peuvent être difficiles, voire impossibles à coder. Afin de faciliter leur écriture, les sous-modèles doivent notamment être très paramétrables. Ils doivent offrir suffisamment de degrés de liberté pour pouvoir d'abord se fondre dans la représentation grossière puis faire apparaître continûment leurs détails. Malheureusement, lors de la réalisation d'un seul sous-modèle, il est très facile de négliger ces degrés de liberté nécessaires à une future mise en commun multi-échelle. Ici encore, un environnement de travail peut imposer une certaine discipline ou tout du moins faciliter le plus possible le paramétrage d'un modèle.

3.3.4.6 Cahier des charges

Dans cette thèse, nous proposons un nouveau modeleur générique multi-échelle présenté dans les chapitres 5, 6 et 7. Nous avons identifié une liste de fonctionnalités dont ce dernier doit être muni :

Sachant que la modélisation par complexification est dirigée par la loi du cas particulier, les choix réalisés pour cet environnement ne doivent en aucun cas restreindre l'éventail des modèles possibles. Clairement, on prend le risque d'imposer un certain style de modélisation mais ce constat est valable pour n'importe quel outil de modélisation. De plus, toutes les fonctionnalités listées plus haut peuvent paraître ambitieuses. Pourtant, l'objectif à atteindre est finalement relativement modeste : il s'agit de rendre meilleures les conditions actuelles de modélisation par complexification. Ces conditions étant actuellement très médiocres (quasi-inexistantes), il y a beaucoup de place pour l'amélioration.

Avant de passer à la description de nos contributions à ce problème, le chapitre suivant revient sur l'étude préliminaire d'un cas particulier : l'animation temps-réel de prairies agitées par le vent.