AnimaL |
Tutorial |
Documentation |
Functions | |
| template<class M1, class M2> void | animal::m_eq_ludcmp (M1 &LU, const M2 &A) |
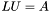 (precond: &A!=&LU) LU decomposition of matrix A. (precond: &A!=&LU) LU decomposition of matrix A. | |
| template<class M, class V1, class V2> void | animal::v_eq_lusolve (V1 &x, const M &LU, const V2 &b) |
Solve 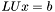 . . | |
| template<class M, class M2, class Vec> void | animal::m_eq_luinv (M &Inv, const M2 &LU, Vec &aux) |
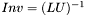 Inverse of a matrix given its LU decomposition. Inverse of a matrix given its LU decomposition. | |
| template<class M, class M2> int | animal::ludcmp (M &a, M2 indx) |
| template<class M, class M2, class M3> int | animal::lubksb (M &a, M2 indx, M3 b) |
| template<class M> int | animal::ns1__luinv (M &a, M &b) |
| template<class M1, class M2> void | animal::m_eq_modchol (M1 &L, const M2 &A) |
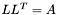 (precond: &A!=&L) Modified cholesky decomposition of matrix A. (precond: &A!=&L) Modified cholesky decomposition of matrix A. | |
| template<class M, class V1, class V2> void | animal::v_eq_cholsolve (V1 &x, const M &L, const V2 &b) |
| Solution of a linear equation system using the modified Cholesky decomposition L of the system matrix A (see m_eq_modchol). | |
| template<class M, class M2, class M3> void | animal::m_eq_cholinv (M &Inv, const M2 &A, M3 &Tmp) |
| Inverse of a symmetric positive definite matrix. | |
| template<class M1, class M2> void | animal::m_eq_invsqrt (M1 &B, const M2 &A) |
compute 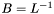 , where , where 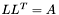 . . | |
| template<class M1, class M2> void | animal::m_eq_cholfactor (M1 &L, const M2 &A) |
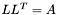 (precond: &A!=&L) Cholesky decomposition of matrix A. (precond: &A!=&L) Cholesky decomposition of matrix A. | |
| template<class M1, class M2> void | animal::m_eq_invsqrt2 (M1 &B, const M2 &A) |
compute 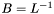 , where , where 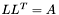 . . | |
| template<class M1, class M2> void | animal::m_eq_inv (M1 &B, const M2 &A) |
compute 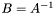 | |
|
||||||||||||||||||||
|
Definition at line 1314 of file linear.h. References animal::nrows(). Referenced by animal::ns1__luinv(). |
|
||||||||||||||||
|
Definition at line 1248 of file linear.h. References animal::nrows(). Referenced by animal::ns1__luinv(). |
|
||||||||||||||||
|
Only the upper triangular part of A is used. The lower triangular part of L is written.
Definition at line 1513 of file linear.h. References animal::ncols(), and animal::nrows(). Referenced by animal::m_eq_invsqrt2(). |
|
||||||||||||||||||||
|
Inverse of a symmetric positive definite matrix. (precond: &A!=&Tmp and &Inv!=&Tmp)
Definition at line 1465 of file linear.h. References animal::m_eq_AtB(), and animal::m_eq_invsqrt(). |
|
||||||||||||||||
|
compute
Definition at line 1595 of file linear.h. References animal::ncols(), and animal::nrows(). |
|
||||||||||||||||
|
compute
Definition at line 1479 of file linear.h. References animal::m_eq_modchol(), animal::ncols(), and animal::nrows(). Referenced by animal::m_eq_cholinv(). |
|
||||||||||||||||
|
compute
Definition at line 1559 of file linear.h. References animal::m_eq_cholfactor(), animal::ncols(), and animal::nrows(). |
|
||||||||||||||||
|
Matrix L is stored in the lower triangle of LU, including the diagonal. Matrix U is stored in the strictly upper triangular part of LU. Since the diagonal entries of U are all equal to 1, they are not stored.
Definition at line 1140 of file linear.h. References animal::ncols(), and animal::nrows(). Referenced by animal::octree::getMatrixInverse(). |
|
||||||||||||||||||||
|
(precond: &Inv!=&LU)
Definition at line 1213 of file linear.h. References animal::ncols(), animal::nrows(), animal::size(), and animal::v_assign(). Referenced by animal::b_eq_inverse(), and animal::octree::getMatrixInverse(). |
|
||||||||||||||||
|
Only the upper triangular part of A is used. The lower triangular part of L is written. The values of the diagonal of L are inversed (1/) with respect to the real cholesky decomposition. This accelerates the solution of an equation system based on this decomposition. Consequently,
Definition at line 1395 of file linear.h. References animal::ncols(), and animal::nrows(). Referenced by animal::m_eq_invsqrt(). |
|
||||||||||||||||
|
Definition at line 1352 of file linear.h. References animal::lubksb(), animal::ludcmp(), and animal::nrows(). |
|
||||||||||||||||||||
|
Solution of a linear equation system using the modified Cholesky decomposition L of the system matrix A (see m_eq_modchol).
Given L and vector b, the method computes x such that
Definition at line 1430 of file linear.h. References animal::ncols(), animal::nrows(), and animal::size(). |
|
||||||||||||||||||||
|
Solve
Solution of a linear equation system using the LU decomposition of a matrix A. Given matrix LU and vector b, the method computes vector x such that
Definition at line 1180 of file linear.h. References animal::ncols(), animal::nrows(), and animal::size(). |
 1.3.6
1.3.6