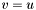Documentation

linear.readme File Reference

Detailed Description

Linear algebra template methods implemented in linear.h.

vector vector-vector matrix matrix-matrix matrix-vector factorization and solution
$ size $ animal::size(Cont&)
$ v = a $ animal::v_assign(Cont&,const typename container_traits<Cont>::value_type&)
$ v *= a $ animal::v_teq(Cont& Y, typename container_traits<Cont>::value_type a)
$ \| v \| $ animal::v_norm(const Cont&)
$ v = v/\|v\| $ animal::v_normalize(Cont&)
$ \| v \|_1 $ animal::v_norm1
$ \| v \|_{\inf} $ animal::v_normInf(const Cont&)
$ \sum_i v_i $ animal::v_sum(const Cont&)
$ \sum_i v_i^2 $ animal::v_sqsum(const Cont&)
$ \frac{1}{dim(v)} \sum_i v_i $ animal::v_mean(const Cont&)
$ variance(v) $ animal::v_variance(const Cont&)

$ v=u $ animal::v_eq(Cont&,const Cont&)
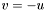$ v=-u $ animal::v_meq(Cont&,const Cont&)
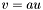$ v=au $ animal::v_eq (Cont&,typename container_traits<Cont>::value_type,const Cont&)
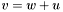$ v=w+u $ animal::v_eq_apb(Cont&,const Cont&,const Cont&)
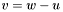$ v=w-u $ animal::v_eq_amb(Cont&,const Cont& a,const Cont& b)
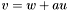$ v=w+au $ animal::v_eq (Cont&,const Cont&,typename container_traits<Cont>::value_type,const Cont&)

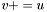$ v+=u $ animal::v_peq (Cont&,const Cont&)
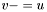$ v-=u $ animal::v_meq (Cont&,const Cont&)
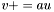$ v+=au $ animal::v_peq (Cont&,typename container_traits<Cont>::value_type,const Cont&)

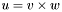$ u = v \times w $ animal::v_eq_cross (V1&,const V2&,const V3&)
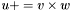$ u += v \times w $ animal::v_peq_cross (V1&,const V2&,const V3&)
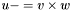$ u -= v \times w $ animal::v_meq_cross (V1&,const V2&,const V3&)

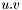$ u.v $ animal::v_dot(const Cont&,const Cont&)

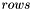$ rows $ animal::nrows(const M&)
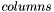$ columns $ animal::ncols(const M& m)
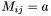$ M_{ij} = a $ animal::m_assign( Cont& M, const typename matrix_traits<Cont>::value_type a )
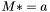$ M *= a $ animal::m_teq ( Cont& M, const typename matrix_traits<Cont>::value_type a )

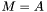$ M=A $ animal:: m_eq_A (Cont1&,const Cont2&)
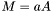$ M=aA $ animal::m_eq_aA (Cont1&,typename matrix_traits<Cont2>::value_type,const Cont2&)
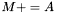$ M+=A $ animal::m_peq_A (Cont1&,const Cont2&)
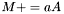$ M+=aA $ animal::m_peq_aA (Cont1&,typename matrix_traits<Cont2>::value_type,const Cont2&)
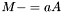$ M-=aA $ animal::m_meq_A (Cont1& M,const Cont2&)

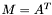$ M=A^T $ animal:: m_eq_At (Cont1&,const Cont2&)
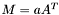$ M=aA^T $ animal::m_eq_aAt (Cont1&,typename matrix_traits<Cont2>::value_type,const Cont2&)
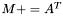$ M+=A^T $ animal::m_peq_At (Cont1&,const Cont2&)
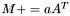$ M+=aA^T $ animal::m_peq_aAt (Cont1&,typename matrix_traits<Cont2>::value_type,const Cont2&)
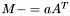$ M-=aA^T $ animal::m_meq_At (Cont1& M,const Cont2&)

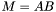$ M=AB $ animal::m_eq_AB ( M1& C, const M2& A, const M3& B )
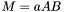$ M=aAB $ animal::m_eq_aAB ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
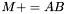$ M+=AB$ animal::m_peq_AB ( M1& C, const M2& A, const M3& B )
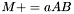$ M+=aAB$ animal::m_peq_aAB ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
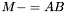$ M-=AB $ animal::m_meq_AB ( M1& C, const M2& A, const M3& B )

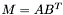$ M=AB^T $ animal::m_eq_ABt ( M1& C, const M2& A, const M3& B )
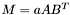$ M=aAB^T $ animal::m_eq_aABt ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
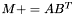$ M+=AB^T $ animal::m_peq_ABt ( M1& C, const M2& A, const M3& B )
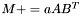$ M+=aAB^T$ animal::m_peq_aABt ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
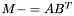$ M-=AB^T $ animal::m_meq_ABt ( M1& C, const M2& A, const M3& B )

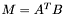$ M=A^TB $ animal::m_eq_AtB ( M1& C, const M2& A, const M3& B )
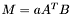$ M=aA^TB $ animal::m_eq_aAtB ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
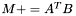$ M+=A^TB$ animal::m_peq_AtB ( M1& C, const M2& A, const M3& B )
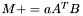$ M+=aA^TB$ animal::m_peq_aAtB ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
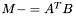$ M-=A^TB $ animal::m_meq_AtB ( M1& C, const M2& A, const M3& B )

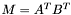$ M=A^TB^T $ animal::m_eq_AtBt ( M1& C, const M2& A, const M3& B )
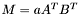$ M=aA^TB^T $ animal::m_eq_aAtBt ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
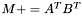$ M+=A^TB^T $ animal::m_peq_AtBt ( M1& C, const M2& A, const M3& B )
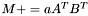$ M+=aA^TB^T$ animal::m_peq_aAtBt ( M1& C, const typename matrix_traits<M2>::value_type a, const M2& A, const M3& B )
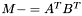$ M-=A^TB^T $ animal::m_meq_AtBt ( M1& C, const M2& A, const M3& B )

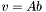$ v=Ab $ animal::v_eq_Ab ( V1& v, const M& A, const V2& b )
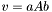$ v=aAb $ animal::v_eq_aAb ( V1& v, const typename matrix_traits<M>::value_type a, const M& A, const V2& b
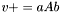$ v+=aAb $ animal::v_peq_aAb ( V1& v, const typename matrix_traits<M>::value_type a, const M& A, const V2& b )
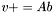$ v+=Ab $ animal::v_peq_Ab ( V1& v, const M& A, const V2& b )
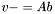$ v-=Ab $ animal::v_meq_Ab ( V1& v, const M& A, const V2& b )

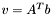$ v=A^Tb $ animal::v_eq_Atb ( V1& v, const M& A, const V2& b )
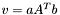$ v=aA^Tb $ animal::v_eq_aAtb ( V1& v, const typename matrix_traits<M>::value_type a, const M& A, const V2& b
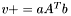$ v+=aA^Tb $ animal::v_peq_aAtb ( V1& v, const typename matrix_traits<M>::value_type a, const M& A, const V2& b )
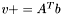$ v+=A^Tb $ animal::v_peq_Atb ( V1& v, const M& A, const V2& b )
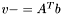$ v-=A^Tb $ animal::v_meq_Atb ( V1& v, const M& A, const V2& b )

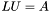$ LU = A $ animal::m_eq_ludcmp( M1& LU, const M2& A )
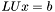$ LUx = b $ animal::v_eq_lusolve( V1& x, const M& LU, const V2& b )
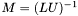$ M=(LU)^{-1} $ animal::m_eq_luinv( M& Inv, const M2& LU, Vec& aux )
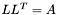$ LL^T = A $ animal::m_eq_modchol( M1& L, const M2& A )
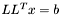$ LL^Tx = b $ animal::v_eq_cholsolve( V1& x, const M& L, const V2& b )
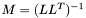$ M=(LL^T)^{-1} $ animal::m_eq_cholinv( M& Inv, const M2& A, M3& Tmp )
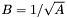$ B = 1/\sqrt{A} $ animal::m_eq_invsqrt(M1& B , const M2& A)

Definition in file linear.readme.

Go to the source code of this file.

Generated on Thu Dec 23 13:52:28 2004 by doxygen 1.3.6