AnimaL |
Tutorial |
Documentation |
A class to represent a 3D DataType vector.
Classes | |
| struct | ArgumentBase |
| Abstract base class for all comand line arguments. More... | |
| struct | Argument |
| Command line argument. Contains a pointer to a value which can be parsed by a ArgumentParser. More... | |
| class | ArgumentParser |
| Command line parser. More... | |
| struct | Array |
| Fixed-size array. More... | |
| struct | Value< Array< N, T > > |
| Null values. More... | |
| struct | Frame |
| Origin and basis of a local frame (coordinate system) with respect to a reference frame (coordinate system). More... | |
| class | BoundingBox3D |
| Axis-aligned bounding box in dimension 3. More... | |
| class | Chrono |
| A Chronometers class. More... | |
| struct | container_traits |
| Abstraction of a container. More... | |
| struct | container_traits< Cont const > |
| Abstraction of a const container. More... | |
| struct | container_traits< T[sz]> |
| Abstraction of a container: overlaoded version for arrays. More... | |
| struct | container_traits< T const[sz]> |
| Abstraction of a const container: overlaoded version for const arrays. More... | |
| struct | value_type |
| class | FrprMinimizer |
| Function optimization using gradient. More... | |
| class | History |
| Base class for histories (single values or stl containers). More... | |
| struct | History::Key |
| Store a time stamp: time, position, velocity. More... | |
| class | HistoryS |
| History for single values with << and >> operators. More... | |
| class | HistoryV |
| History for STL containers. More... | |
| class | ExplicitIntegrator |
| Apply explicit time integration of a given function. More... | |
| struct | States |
| States: position, velocity. More... | |
| struct | Derivs |
| Derivative: velocity, acceleration. More... | |
| class | ExplicitIntegrator2 |
| Apply explicit time integration of a given function for second-order differential equation: acceleration(position, velocity) Handles auxiliary variables and their resizing. More... | |
| struct | ExplicitIntegrator2::Derivator |
| Compute a Derivative given a State. More... | |
| struct | v_Output |
| Vector output. More... | |
| struct | v_Input |
| Vector input. Sets the values of the elements. More... | |
| struct | m_Output |
| matrix output More... | |
| struct | m_Input |
| matrix input. Sets the values of the elements. More... | |
| struct | matrix_traits |
| Auxiliary class for the extraction of matrix entry type. More... | |
| class | MassSpringSolver |
| A solver for mass-spring systems. More... | |
| struct | matrix_traits< Matrix< T > > |
| Entry type (specialize if necessary). More... | |
| struct | Matrix |
| Dense 2d array stored as a dense 1d array. More... | |
| class | Numerics |
| Numerics general template. More... | |
| class | Numerics< float > |
| Numerics<float>: specialization of class Numerics<>. More... | |
| class | Numerics< double > |
| Numerics<double>: specialization of class Numerics<>. More... | |
| class | OdeImplicitSolver |
| Abstract class for implicit ODE solver. More... | |
| class | OdeSolver |
| Abstract class for ODE solvers. More... | |
| class | PhysicalSolver |
| This is a base class for physically-based animation of points (gravity, air damping). More... | |
| class | ConstrainedItem |
| Models something which can be selected and moved interactively. More... | |
| class | Quaternion |
| Unit quaternion used to model a rotation in 3D. More... | |
| class | Quaternion_Traits |
| class | Rotation2d |
| Matrix 2x2 used to model a rotation in 2D. More... | |
| class | Rotation2d_Traits |
| Customization of class rotation in 2D. More... | |
| class | SimpleSolver |
| This is a base class for physically-based animation of points (gravity, air damping). More... | |
| struct | Value |
| class | vector |
| Same as std::vector, + range checking on operator[ ]. More... | |
| struct | VectorVec |
| A vector of vectors. More... | |
| class | World |
| Abstract base class to represent the world of a 3D scene. More... | |
| class | Engine |
| Abstract base class to represent an animation concept. More... | |
| class | MassSpringEngine |
| This class implements a physical engine which animates particules (defined with Inv_Masses, Velocities and Points) linked with springs (defined with SpringStiffness and IndexedSprings). More... | |
| class | MassSpringEngine::ConstrainedPoint |
| Models a selected point among a vector of points, using a pointer to the engine and the index of the point. More... | |
| struct | MassSpringEngine::rgb |
| class | MorphingEngine |
| This class computes an interpolation from given values which are defined at several keys. More... | |
| class | Event |
| The AnimalEvent class is the base class of all event classes. Event objects contain event parameters. More... | |
| class | KeyEvent |
| The AnimalKeyEvent class describes a key event. More... | |
| class | MouseEvent |
| The AnimalMouseEvent class describes a mouse event. More... | |
| class | EngineGroup |
| Recursively apply the actions. More... | |
| struct | container_traits< X3DTK::SFVec3f > |
| Abstraction of a SFVe3f. More... | |
| struct | container_traits< X3DTK::SFVec3f const > |
| Abstraction of a SFVe3f const. More... | |
| struct | Value< X3DTK::SFVec3f > |
| struct | value_type< X3DTK::SFVec3f > |
BoundingBox3D class-related methods. | |
| template<class P, class R> std::ostream & | operator<< (std::ostream &os, const BoundingBox3D< P, R > &b) |
| Output. | |
| template<class P, class R> bool | intersect (const BoundingBox3D< P, R > &b1, const BoundingBox3D< P, R > &b2) |
| Test bounding box intersection. | |
vector and matrix input/output | |
| template<class Container> void | print (const Container &container) |
| Print all the values of a container on the standard output. | |
| template<class Container> void | print (const Container &container, std::ostream &out) |
| Print all the values of a container on the specified output. | |
| template<class T> v_Output< T > | v_output (const T &t, char *s="") |
| to put a vector in an output stream | |
| template<class T> std::ostream & | operator<< (std::ostream &out, v_Output< T > ot) |
| output a vector | |
| template<class T> v_Input< T > | v_input (T &t) |
| to put a vector in an input stream | |
| template<class T> std::istream & | operator>> (std::istream &in, v_Input< T > it) |
| input a vector | |
| template<class T> m_Output< T > | m_output (const T &t) |
| to put a matrix in an output stream | |
| template<class T> std::ostream & | operator<< (std::ostream &out, m_Output< T > ot) |
| matrix output | |
| template<class T> m_Input< T > | m_input (T &t) |
| to put a matrix in an input stream | |
| template<class T> std::istream & | operator>> (std::istream &in, m_Input< T > it) |
| matrix input | |
Quaternion class-related methods | |
| template<class Real, class Traits> std::ostream & | operator<< (std::ostream &stream, const Quaternion< Real, Traits > &q) |
| Output stream. | |
| template<class Real, class Traits> std::istream & | operator>> (std::istream &stream, Quaternion< Real, Traits > &q) |
| Input stream. | |
| template<class Real, class Traits> Vec3 | operator * (const typename Quaternion< Real, Traits >::Vec3 &, const Quaternion< Real, Traits > &) |
| Apply rotation to a vector. | |
| template<class Real, class Traits> Vec3 | operator/ (const typename Quaternion< Real, Traits >::Vec3 &, const Quaternion< Real, Traits > &) |
| Apply inverse rotation to a vector. | |
| template<class Real, class Traits, class Mat33> void | writeRotMatrix (const Quaternion< Real, Traits > &q, Mat33 &m) |
| template<class Real, class Traits, class Mat44> void | writeOpenGLRotMatrix (const Quaternion< Real, Traits > &q, Mat44 &m) |
Rotation2d class-related methods | |
| template<class R, class T, class Vector> Vector | operator/ (const Vector &v, const Rotation2d< R, T > &m) |
| Apply inverse rotation to a vector. | |
| template<class R, class T, class Vector> Vector & | operator/= (Vector &v, const Rotation2d< R, T > &m) |
| Apply inverse rotation to a vector. | |
| template<class R, class T, class Vector> Vector | operator * (const Vector &v, const Rotation2d< R, T > &m) |
| Apply rotation to a vector. | |
| template<class R, class T, class Vector> Vector & | operator *= (Vector &v, const Rotation2d< R, T > &m) |
| Apply rotation to a vector. | |
| template<class R, class T> std::istream & | operator>> (std::istream &stream, Rotation2d< R, T > &r) |
| Input. | |
| template<class R, class T> std::ostream & | operator<< (std::ostream &stream, const Rotation2d< R, T > &r) |
| Output. | |
vector class-related methods | |
| template<class T, class TT> void | remove (std::vector< T, TT > &v, const T &elem) |
| Remove the first occurence of a given value. | |
| template<class T, class TT> void | removeValue (std::vector< T, TT > &v, const T &elem) |
| Remove the first occurence of a given value. | |
| template<class T, class TT> void | removeIndex (std::vector< T, TT > &v, size_t index) |
| Remove value at given index, replace it by the value at the last index, other values are not changed. | |
Typedefs | |
| typedef std::istringstream | istrstream |
| use a string as input | |
| typedef unsigned int | Natural |
| Positive integer, used as size_type. | |
| typedef Array< 2, float > | Vec2 |
| Specialization of animal::Array with two float. | |
| typedef Array< 3, float > | Vec3 |
| Specialization of animal::Array with three float. | |
| typedef Array< 4, float > | Vec4 |
| Specialization of animal::Array with four float, in order to describe RGBA datas or rotations. | |
Functions | |
| ArgumentParser | parse (const std::string &helpstr="", char hs='h', const std::string &hl="help") |
| parse | |
| template<class T, std::size_t N> Array< N, T > | operator * (const T &a, const Array< N, T > &v) |
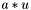 where a is a scalar where a is a scalar | |
| template<class T, std::size_t N> std::ostream & | operator<< (std::ostream &out, const Array< N, T > &a) |
| Write to an output stream. | |
| template<class T, std::size_t N> std::istream & | operator>> (std::istream &in, Array< N, T > &a) |
| Read from an input stream. | |
| template<class Vec1, class Basis, class Vec2> void | v_eq_project_vec (Vec1 &v, const Basis &b, const Vec2 &a) |
| Project vector a from basis b to another base. | |
| template<class Basis1, class Basis2> void | b_eq_inverse (Basis1 &b, const Basis2 &a) |
| Compute inverse of basis a and stores it in b. | |
| template<class Basis, class Real> void | b_eq_eulerX (Basis &b, Real a) |
| Define a basis as a given rigid rotation defined by one Euler angle a around axis i. | |
| template<class Basis, class Real> void | b_eq_eulerY (Basis &b, Real a) |
| Define a basis as a given rigid rotation defined by one Euler angle a around axis j. | |
| template<class Basis, class Real> void | b_eq_eulerZ (Basis &b, Real a) |
| Define a basis as a given rigid rotation defined by one Euler angle a around axis k. | |
| template<class Basis, class Real> void | b_eq_eulerXYZ (Basis &b, Real a, Real b, Real c) |
| Define a basis as a given rigid rotation defined by Euler angles around axes i then j then k. | |
| template<class Vec1, class Frame, class Vec2> void | v_eq_project_point (Vec1 &v, const Frame &f, const Vec2 &a) |
| template<class Frame> void | f_eq_inverse (Frame &f, const Frame &a) |
| template<class Basis, class Vec> const Vec & | get_translation (const Frame< Basis, Vec > &f) |
| Read-only reference to the translation of a frame. | |
| template<class Basis, class Vec> Vec & | set_translation (Frame< Basis, Vec > &f) |
| Read-write reference to the translation of a frame. | |
| template<class Basis, class Vec> const Basis & | get_basis (const Frame< Basis, Vec > &f) |
| Read-only reference to the basis of a frame. | |
| template<class Basis, class Vec> Basis & | set_basis (Frame< Basis, Vec > &f) |
| Read-write reference to the basis of a frame. | |
| template<typename Cont> container_traits< Cont >::iterator | begin (Cont &cont) |
| First element of a sequence. | |
| template<typename Cont> container_traits< Cont >::iterator | end (Cont &cont) |
| Element after the last element of a sequence. | |
| template<typename Cont> container_traits< Cont >::size_type | size (Cont &cont) |
| Size of a sequence. | |
| template<typename T, std::size_t sz> container_traits< T[sz]>::iterator | begin (T(&a)[sz]) |
| First element of an array. | |
| template<typename T, std::size_t sz> container_traits< T[sz]>::iterator | end (T(&a)[sz]) |
| Element after the last element of an array. | |
| template<typename T, std::size_t sz> container_traits< T[sz]>::size_type | size (T(&a)[sz]) |
| Size of an array. | |
| template<class FS, class IS, class D, class Real> void | v_eq_euler_step (FS &final, const IS &initial, Real h, const D &derivative) |
| Apply an euler integration step final = initial + h*deriv. | |
| template<class State, class Deriv, class Derivator, class Real> void | integrate_euler (State &s, Real h, Derivator *eq_deriv, Real t, Deriv &d) |
| Perform one Euler integration step: x += h*x'(x). | |
| template<class State, class Deriv, class Derivator, class StateAux, class Real> void | integrate_rk2 (State &s, Real h, Derivator *eq_deriv, Real t, Deriv &d, StateAux &s1) |
| Perform one second-order Runge-Kutta integration step. | |
| template<class State, class Deriv, class Derivator, class StateAux, class Real> void | integrate_rk4 (State &s, Real h, Derivator *eq_deriv, Real t, Deriv &d1, Deriv &d2, Deriv &d3, Deriv &d4, StateAux &s1) |
| Perform one fourth-order Runge-Kutta integration step. | |
| template<class State, class Deriv, class Derivator, class StateAux, class Real> void | integrate_modmid (State &s, Real h, Derivator *eq_deriv, Real t, int n, Deriv &d1, StateAux &s1, StateAux &s2, StateAux &s3) |
| Perform one modified midpoint integration step. | |
| template<class P, class V> void | v_eq (States< P, V > &s, const States< P, V > &t) |
| copy a States | |
| template<class P, class V> void | v_peq (States< P, V > &s, const States< P, V > &t) |
| Add two states component-wise. | |
| template<class P, class V, class Real> void | v_eq_ab (States< P, V > &s, const Real &a, const States< P, V > &b) |
| Set a state to a real time a state. | |
| template<class V, class A> void | v_peq (Derivs< V, A > &d, const Derivs< V, A > &e) |
| Add derivatives component-wise. | |
| template<class V, class A, class Real> void | v_teq (Derivs< V, A > &d, const Real &e) |
| multiply derivative by a real | |
| template<class C1, class C2> std::ostream & | operator<< (std::ostream &out, const std::pair< C1, C2 > &p) |
| print an std::pair | |
| template<class C1, class C2> std::istream & | operator>> (std::istream &in, std::pair< C1, C2 > &p) |
| read an std::pair | |
| template<class Cont, class Value> void | v_assign (Cont &v, const Value &a) |
Assign a value to all the entries ![$ \forall i \;\; v[i] = a $](form_84.png) . . | |
| template<class Cont, class Value> void | v_addall (Cont &v, const Value &a) |
Add a value to all the entries ![$ \forall i \;\; v[i] = a $](form_84.png) . . | |
| template<class Cont, class Real> void | v_teq (Cont &v, const Real &a) |
![$\forall i \;\; v[i] = *a $](form_85.png) | |
| template<class Cont> value_type< Cont >::type | v_norm (const Cont &v) |
norm 2 of vector ![$ \sqrt{ \sum_i v[i]^2 } $](form_86.png) Euclidian norm Euclidian norm | |
| template<class Cont> void | v_normalize (Cont &v) |
normalize the vector: 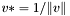 | |
| template<class Cont> container_traits< Cont >::value_type | v_norm1 (const Cont &v) |
norm 1 of vector ![$ \sum_i |v[i]| $](form_88.png) Sum of all absolute values of the entries Sum of all absolute values of the entries | |
| template<class Cont> container_traits< Cont >::value_type | v_normInf (const Cont &v) |
infinite norm of vector ![$ \max_i |v[i]| $](form_89.png) The maximum absolute value among all the entries The maximum absolute value among all the entries | |
| template<class Cont> container_traits< Cont >::value_type | v_sum (const Cont &v) |
sum of vector elements ![$ \sum_i v[i] $](form_90.png) | |
| template<class Cont> container_traits< Cont >::value_type | v_sqsum (const Cont &v) |
the sum of the squares of the vector entries ![$ \sum_i v[i]^2 $](form_91.png) | |
| template<class Cont> container_traits< Cont >::value_type | v_mean (const Cont &v) |
the mean of vector entries ![$ \sum_i v[i] / size(v)$](form_92.png) | |
| template<class Cont> container_traits< Cont >::value_type | v_variance (const Cont &v) |
variance of vector elements ![$ \sum_i (v[i]-\bar{v})^2 / size(v) $](form_93.png) | |
| template<class Cont1, class Cont2> void | v_eq (Cont1 &Y, const Cont2 &X) |
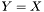 | |
| template<class Cont1, class Cont2> void | v_eq_minus (Cont1 &Y, const Cont2 &X) |
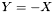 | |
| template<class Cont1, class Cont2, class Real> void | v_eq_ab (Cont1 &Y, const Real &a, const Cont2 &X) |
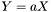 | |
| template<class Cont1, class Cont2, class Cont3> void | v_eq_apb (Cont1 &Y, const Cont2 &W, const Cont3 &X) |
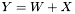 | |
| template<class Cont1, class Cont2, class Cont3> void | v_eq_amb (Cont1 &Y, const Cont2 &W, const Cont3 &X) |
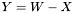 | |
| template<class Cont1, class Cont2, class Cont3, class Entry> void | v_eq (Cont1 &Y, const Cont2 &W, const Entry &a, const Cont3 &X) |
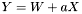 | |
| template<class Cont1, class Cont2> void | v_peq (Cont1 &Y, const Cont2 &X) |
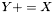 | |
| template<class Cont> void | v_meq (Cont &Y, const Cont &X) |
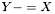 | |
| template<class Cont> void | v_peq (Cont &y, typename container_traits< Cont >::value_type a, const Cont &x) |
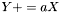 | |
| template<class Cont> void | v_meq (Cont &y, typename container_traits< Cont >::value_type a, const Cont &x) |
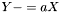 | |
| template<class Cont, class Real> void | v_peq_ab (Cont &y, Real a, const Cont &x) |
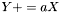 | |
| template<class V1, class V2, class V3> void | v_eq_cross (V1 &u, const V2 &v, const V3 &w) |
Cross product of two vectors: 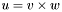 (generalisation of cross product in dimension 3). (Precond: &u!=&v and &u!=&w). (generalisation of cross product in dimension 3). (Precond: &u!=&v and &u!=&w). | |
| template<class V1, class V2, class V3> void | v_peq_cross (V1 &u, const V2 &v, const V3 &w) |
Add cross product of two vectors: 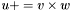 . (Precond: &u!=&v and &u!=&w). . (Precond: &u!=&v and &u!=&w). | |
| template<class V1, class V2, class V3> void | v_meq_cross (V1 &u, const V2 &v, const V3 &w) |
Substract cross product of two vectors: 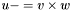 . (Precond: &u!=&v and &u!=&w). . (Precond: &u!=&v and &u!=&w). | |
| template<class Cont> value_type< Cont >::type | v_dot (const Cont &x, const Cont &y) |
| dot product of two vectors | |
| template<class M> std::size_t | nrows (const M &m) |
| Number of rows of a matrix. | |
| template<class M> std::size_t | ncols (const M &m) |
| Number of columns of a matrix. | |
| template<class Cont, class Value> void | m_assign (Cont &M, const Value &a) |
for all elements M[i][j]: ![$ M[i][j] = a $](form_104.png) | |
| template<class Cont, class Val> void | m_teq (Cont &M, const Val &a) |
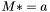 | |
| template<class Cont, class Val> void | m_deq (Cont &M, const Val &a) |
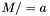 | |
| template<class Cont1, class Cont2> void | m_eq_A (Cont1 &M, const Cont2 &A) |
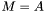 | |
| template<class Cont1, class Cont2> void | m_eq_aA (Cont1 &M, typename matrix_traits< Cont2 >::value_type a, const Cont2 &A) |
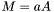 | |
| template<class Cont1, class Cont2> void | m_peq_A (Cont1 &M, const Cont2 &A) |
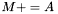 | |
| template<class Cont1, class Cont2> void | m_peq_aA (Cont1 &M, typename matrix_traits< Cont2 >::value_type a, const Cont2 &A) |
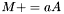 | |
| template<class Cont1, class Cont2> void | m_meq_A (Cont1 &M, const Cont2 &A) |
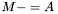 | |
| template<class Cont1, class Cont2> void | m_eq_At (Cont1 &M, const Cont2 &A) |
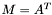 | |
| template<class Cont1, class Cont2> void | m_eq_aAt (Cont1 &M, typename matrix_traits< Cont2 >::value_type a, const Cont2 &A) |
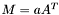 | |
| template<class Cont1, class Cont2> void | m_peq_At (Cont1 &M, const Cont2 &A) |
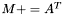 | |
| template<class Cont1, class Cont2> void | m_peq_aAt (Cont1 &M, const typename matrix_traits< Cont2 >::value_type a, const Cont2 &A) |
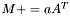 | |
| template<class Cont1, class Cont2> void | m_meq_At (Cont1 &M, const Cont2 &A) |
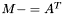 | |
| template<class M1, class M2, class M3> void | m_eq_AB (M1 &C, const M2 &A, const M3 &B) |
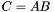 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_aAB (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
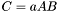 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_AB (M1 &C, const M2 &A, const M3 &B) |
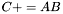 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_aAB (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
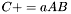 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_meq_AB (M1 &C, const M2 &A, const M3 &B) |
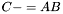 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_ABt (M1 &C, const M2 &A, const M3 &B) |
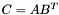 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_aABt (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
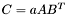 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_ABt (M1 &C, const M2 &A, const M3 &B) |
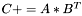 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_aABt (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
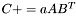 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_meq_ABt (M1 &C, const M2 &A, const M3 &B) |
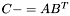 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_AtB (M1 &C, const M2 &A, const M3 &B) |
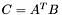 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_aAtB (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
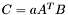 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_AtB (M1 &C, const M2 &A, const M3 &B) |
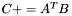 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_aAtB (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
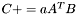 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_meq_AtB (M1 &C, const M2 &A, const M3 &B) |
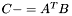 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_AtBt (M1 &C, const M2 &A, const M3 &B) |
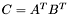 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_eq_aAtBt (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
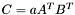 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_AtBt (M1 &C, const M2 &A, const M3 &B) |
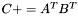 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_peq_aAtBt (M1 &C, const typename matrix_traits< M2 >::value_type a, const M2 &A, const M3 &B) |
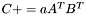 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class M1, class M2, class M3> void | m_meq_AtBt (M1 &C, const M2 &A, const M3 &B) |
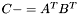 (precond: &C!=&A and &C!=&B) (precond: &C!=&A and &C!=&B) | |
| template<class V1, class M, class V2> void | v_eq_Ab (V1 &v, const M &A, const V2 &b) |
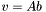 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_eq_aAb (V1 &v, const typename matrix_traits< M >::value_type a, const M &A, const V2 &b) |
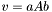 a is scalar (precond: &v!=&b) a is scalar (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_peq_aAb (V1 &v, const typename matrix_traits< M >::value_type a, const M &A, const V2 &b) |
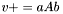 a is scalar (precond: &v!=&b) a is scalar (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_peq_Ab (V1 &v, const M &A, const V2 &b) |
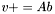 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_meq_Ab (V1 &v, const M &A, const V2 &b) |
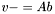 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_eq_Atb (V1 &v, const M &A, const V2 &b) |
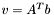 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_eq_aAtb (V1 &v, const typename matrix_traits< M >::value_type a, const M &A, const V2 &b) |
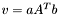 a is scalar (precond: &v!=&b) a is scalar (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_peq_aAtb (V1 &v, const typename matrix_traits< M >::value_type a, const M &A, const V2 &b) |
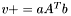 a is scalar (precond: &v!=&b) a is scalar (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_peq_Atb (V1 &v, const M &A, const V2 &b) |
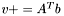 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class V1, class M, class V2> void | v_meq_Atb (V1 &v, const M &A, const V2 &b) |
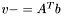 (precond: &v!=&b) (precond: &v!=&b) | |
| template<class M1, class M2> void | m_eq_ludcmp (M1 &LU, const M2 &A) |
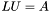 (precond: &A!=&LU) LU decomposition of matrix A. (precond: &A!=&LU) LU decomposition of matrix A. | |
| template<class M, class V1, class V2> void | v_eq_lusolve (V1 &x, const M &LU, const V2 &b) |
Solve 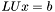 . . | |
| template<class M, class M2, class Vec> void | m_eq_luinv (M &Inv, const M2 &LU, Vec &aux) |
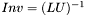 Inverse of a matrix given its LU decomposition. Inverse of a matrix given its LU decomposition. | |
| template<class M, class M2> int | ludcmp (M &a, M2 indx) |
| template<class M, class M2, class M3> int | lubksb (M &a, M2 indx, M3 b) |
| template<class M> int | ns1__luinv (M &a, M &b) |
| template<class M1, class M2> void | m_eq_modchol (M1 &L, const M2 &A) |
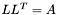 (precond: &A!=&L) Modified cholesky decomposition of matrix A. (precond: &A!=&L) Modified cholesky decomposition of matrix A. | |
| template<class M, class V1, class V2> void | v_eq_cholsolve (V1 &x, const M &L, const V2 &b) |
| Solution of a linear equation system using the modified Cholesky decomposition L of the system matrix A (see m_eq_modchol). | |
| template<class M, class M2, class M3> void | m_eq_cholinv (M &Inv, const M2 &A, M3 &Tmp) |
| Inverse of a symmetric positive definite matrix. | |
| template<class M1, class M2> void | m_eq_invsqrt (M1 &B, const M2 &A) |
compute 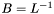 , where , where 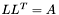 . . | |
| template<class M1, class M2> void | m_eq_cholfactor (M1 &L, const M2 &A) |
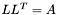 (precond: &A!=&L) Cholesky decomposition of matrix A. (precond: &A!=&L) Cholesky decomposition of matrix A. | |
| template<class M1, class M2> void | m_eq_invsqrt2 (M1 &B, const M2 &A) |
compute 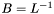 , where , where 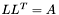 . . | |
| template<class M1, class M2> void | m_eq_inv (M1 &B, const M2 &A) |
compute 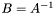 | |
| template<class T> std::size_t | nrows (const Matrix< T > &m) |
| Number of rows. | |
| template<class T> std::size_t | ncols (const Matrix< T > &m) |
| Number of columns. | |
| template<class T> const Matrix< T > & | m_output (const Matrix< T > &m) |
| for compatibility with animal::io | |
| template<class T> Matrix< T > & | m_input (Matrix< T > &m) |
| for compatibility with animal::io | |
| template<class T> T | pow2 (const T &f) |
| power two | |
| template<class T> T | pow3 (const T &f) |
| power three | |
| template<class T> T | pow4 (const T &f) |
| power four | |
| template<class Int, class Real, class Points, class Vec> bool | findClosestPointToLine (Int &index, Real &distance, const Points &coords, const Vec &lineOrigin, const Vec &lineDirection, Real threshold) |
| Searches the index of the closest point to the given 3d line among the point array. | |
| template<class T> T | sqr (const T &t) |
| Returns the square of the given value. | |
| template<class T> void | erase (T *&ptr) |
| Free the memory pointed and set the pointer to 0. | |
| template<class V> double | v_dot (const VectorVec< V > &a, const VectorVec< V > &b) |
Overload of the dot product 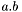 . . | |
| template<class V> void | v_eq (VectorVec< V > &Y, const VectorVec< V > &X) |
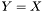 | |
| template<class V> void | v_eq (VectorVec< V > &Y, const VectorVec< V > &W, const double &a, const VectorVec< V > &X) |
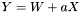 | |
| template<class V> void | v_peq (VectorVec< V > &Y, double a, const VectorVec< V > &X) |
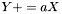 | |
| template<class V> void | v_meq (VectorVec< V > &Y, const VectorVec< V > &X) |
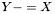 | |
| template<class V> void | v_teq (VectorVec< V > &v, const double &a) |
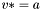 | |
| template<class Container> void | resize (Container &C, int size) |
| std::size_t | size (const X3DTK::SFVec3f &) |
| const float * | begin (const X3DTK::SFVec3f &v) |
| float * | begin (X3DTK::SFVec3f &v) |
| const float * | end (const X3DTK::SFVec3f &v) |
| float * | end (X3DTK::SFVec3f &v) |
| X3DTK::SFVec3f & | operator *= (X3DTK::SFVec3f &v, float f) |
| float | v_dot (const X3DTK::MFVec3f &u, const X3DTK::MFVec3f &v) |
| void | v_peq (X3DTK::MFVec3f &v, const X3DTK::MFVec3f &u) |
| void | v_peq (X3DTK::MFVec3f &v, float a, const X3DTK::MFVec3f &u) |
| float | v_norm (const X3DTK::MFVec3f &u) |
|
|
use a string as input
Definition at line 21 of file argumentParser.h. Referenced by animal::ArgumentParser::operator()(). |
|
|
Positive integer, used as size_type.
Definition at line 21 of file numerics.h. |
|
|
Specialization of animal::Array with two float.
Definition at line 10 of file vec2.h. Referenced by X3DTK::Qt::MFVector2::SFieldGUI(), X3DTK::Qt::SFVector2::SFieldGUI(), and X3DTK::Qt::SFVector2GUI::SFVector2GUI(). |
|
|
Specialization of animal::Array with three float.
Definition at line 11 of file vec3.h. Referenced by animal::Quaternion< RealT, TraitsT >::getAxisAngle(), MainController::mouseDoubleClickEvent(), MainController::mouseMoveEvent(), MainController::mousePressEvent(), and MainController::mouseReleaseEvent(). |
|
|
Specialization of animal::Array with four float, in order to describe RGBA datas or rotations. Warning : this is not a animal::Quaternion more adapted to represent rotations ! Definition at line 12 of file vec4.h. Referenced by X3DTK::Qt::MFVector4::SFieldGUI(), X3DTK::Qt::SFVector4::SFieldGUI(), and X3DTK::Qt::SFVector4GUI::SFVector4GUI(). |
|
|
Definition at line 68 of file linearX3DTK.h. |
|
|
Definition at line 67 of file linearX3DTK.h. |
|
||||||||||
|
First element of an array.
Definition at line 120 of file container_traits.h. |
|
||||||||||
|
First element of a sequence.
Definition at line 102 of file container_traits.h. Referenced by operator<<(), operator>>(), animal::vector< State >::operator[](), v_addall(), v_assign(), v_dot(), v_eq(), v_eq_ab(), v_eq_amb(), v_eq_apb(), v_eq_minus(), v_meq(), v_norm1(), v_normInf(), v_peq(), v_peq_ab(), v_sqsum(), v_sum(), v_teq(), and v_variance(). |
|
|
Definition at line 70 of file linearX3DTK.h. |
|
|
Definition at line 69 of file linearX3DTK.h. |
|
||||||||||
|
Element after the last element of an array.
Definition at line 125 of file container_traits.h. |
|
||||||||||
|
Element after the last element of a sequence.
Definition at line 107 of file container_traits.h. Referenced by operator<<(), operator>>(), v_addall(), v_assign(), v_dot(), v_eq(), v_eq_ab(), v_eq_amb(), v_eq_apb(), v_eq_minus(), v_meq(), v_norm1(), v_normInf(), v_peq(), v_peq_ab(), v_sqsum(), v_sum(), v_teq(), and v_variance(). |
|
||||||||||
|
Free the memory pointed and set the pointer to 0.
|
|
||||||||||||||||||||||||||||||||
|
Searches the index of the closest point to the given 3d line among the point array.
If the distance is smaller than the given threshold, return true. Else, return false (in this case the value of distance is not significant). The threshold is an angular-related value:
Definition at line 47 of file picking.h. References size(), v_dot(), v_meq(), and v_norm(). Referenced by animal::MassSpringEngine< Inv_Masses, Velocities, SpringStiffness, IndexedSprings, Points, Real >::pickPoint(), X3DTK::X3D::DeformableOctreeParticleSystemNode::pickPoint(), and X3DTK::X3D::DeformableOctreeNode::pickPoint(). |
|
||||||||||||||||||||||||||||
|
Perform one Euler integration step: x += h*x'(x).
Definition at line 29 of file integrator.h. References v_eq_euler_step(). Referenced by animal::ExplicitIntegrator2< Position, Velocity, ComputeAcceleration, Real, Acceleration >::euler(), and animal::ExplicitIntegrator< State, Deriv, Derivator, Real >::euler(). |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Perform one modified midpoint integration step.
Definition at line 100 of file integrator.h. References v_eq(), v_eq_ab(), v_eq_euler_step(), and v_peq(). Referenced by animal::ExplicitIntegrator2< Position, Velocity, ComputeAcceleration, Real, Acceleration >::modmid(), and animal::ExplicitIntegrator< State, Deriv, Derivator, Real >::modmid(). |
|
||||||||||||||||||||||||||||||||
|
Perform one second-order Runge-Kutta integration step.
Definition at line 45 of file integrator.h. References v_eq_euler_step(). Referenced by animal::ExplicitIntegrator2< Position, Velocity, ComputeAcceleration, Real, Acceleration >::rk2(), and animal::ExplicitIntegrator< State, Deriv, Derivator, Real >::rk2(). |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Perform one fourth-order Runge-Kutta integration step.
Definition at line 67 of file integrator.h. References v_eq_euler_step(), v_peq(), and v_teq(). Referenced by animal::ExplicitIntegrator2< Position, Velocity, ComputeAcceleration, Real, Acceleration >::rk4(), and animal::ExplicitIntegrator< State, Deriv, Derivator, Real >::rk4(). |
|
||||||||||||||||
|
Test bounding box intersection.
Definition at line 209 of file boundingBox.h. References animal::BoundingBox3D< Point, Real >::_max, and animal::BoundingBox3D< Point, Real >::_min. |
|
||||||||||
|
for compatibility with animal::io
|
|
||||||||||
|
to put a matrix in an input stream
|
|
||||||||||
|
for compatibility with animal::io
|
|
||||||||||
|
to put a matrix in an output stream
|
|
||||||||||
|
Number of columns.
Definition at line 128 of file matrix.h. References animal::Matrix< T >::ncols(). |
|
||||||||||
|
Number of rows.
Definition at line 124 of file matrix.h. References animal::Matrix< T >::nrows(). |
|
||||||||||||||||
|
Apply rotation to a vector.
Definition at line 264 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::_matrix. |
|
||||||||||||||||
|
Apply rotation to a vector.
Definition at line 883 of file quaternion.h. |
|
||||||||||||||||
|
Definition at line 156 of file array.h. References v_teq(). |
|
||||||||||||
|
Definition at line 73 of file linearX3DTK.h. |
|
||||||||||||||||
|
Apply rotation to a vector.
Definition at line 278 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::_matrix. |
|
||||||||||||||||
|
Apply inverse rotation to a vector.
Definition at line 235 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::_matrix. |
|
||||||||||||||||
|
Apply inverse rotation to a vector.
|
|
||||||||||||||||
|
Apply inverse rotation to a vector.
Definition at line 249 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::_matrix. |
|
||||||||||||||||
|
Output.
Definition at line 305 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::angle(). |
|
||||||||||||||||
|
Output stream.
Definition at line 284 of file quaternion.h. |
|
||||||||||||||||
|
print an std::pair
|
|
||||||||||||||||
|
matrix output
Definition at line 135 of file io.h. References begin(), end(), and v_output(). |
|
||||||||||||||||
|
output a vector
|
|
||||||||||||||||
|
Output.
Definition at line 200 of file boundingBox.h. |
|
||||||||||||||||
|
Write to an output stream.
|
|
||||||||||||||||
|
Input.
Definition at line 292 of file rotation2d.h. References animal::Rotation2d< RealT, TraitsT >::setAngle(). |
|
||||||||||||||||
|
Input stream.
Definition at line 297 of file quaternion.h. References animal::Quaternion< RealT, TraitsT >::setAxisAngle(). |
|
||||||||||||||||
|
read an std::pair
|
|
||||||||||||||||
|
matrix input
Definition at line 149 of file io.h. References begin(), end(), animal::m_Input< T >::t, and v_input(). |
|
||||||||||||||||
|
input a vector
Definition at line 119 of file io.h. References begin(), end(), and animal::v_Input< T >::t. |
|
||||||||||||||||
|
Read from an input stream.
|
|
||||||||||||||||
|
parse
Definition at line 359 of file argumentParser.h. |
|
||||||||||
|
power two
Definition at line 12 of file numerics.h. |
|
||||||||||
|
power three
Definition at line 15 of file numerics.h. |
|
||||||||||
|
power four
Definition at line 18 of file numerics.h. |
|
||||||||||||||||
|
Print all the values of a container on the specified output.
|
|
||||||||||
|
Print all the values of a container on the standard output.
|
|
||||||||||||||||
|
Remove the first occurence of a given value. The remaining values are shifted. |
|
||||||||||||||||
|
Remove value at given index, replace it by the value at the last index, other values are not changed.
|
|
||||||||||||||||
|
Remove the first occurence of a given value. The last value is moved to where the value was found, and the other values are not shifted. |
|
||||||||||||||||
|
|
Definition at line 66 of file linearX3DTK.h. |
|
||||||||||
|
Size of an array.
Definition at line 130 of file container_traits.h. |
|
||||||||||
|
||||||||||
|
Returns the square of the given value.
|
|
||||||||||||
|
Definition at line 160 of file linearX3DTK.h. |
|
||||||||||||||||
|
Overload of the dot product
Definition at line 43 of file vectorVec.h. |
|
||||||||||||||||||||||||
|
Definition at line 71 of file vectorVec.h. |
|
||||||||||||||||
|
Definition at line 60 of file vectorVec.h. |
|
||||||||||||||||
|
||||||||||||||||||||
|
||||||||||||||||||||||||
|
Apply an euler integration step final = initial + h*deriv. This is the lowest-level integration method. Definition at line 13 of file integrator.h. References v_eq(). Referenced by animal::OdeSolver< t_Positions, t_Vector, t_Real >::integrate_euler(), integrate_euler(), animal::OdeSolver< t_Positions, t_Vector, t_Real >::integrate_modmid(), integrate_modmid(), animal::OdeSolver< t_Positions, t_Vector, t_Real >::integrate_rk2(), integrate_rk2(), animal::OdeSolver< t_Positions, t_Vector, t_Real >::integrate_rk4(), and integrate_rk4(). |
|
||||||||||
|
to put a vector in an input stream
Definition at line 115 of file io.h. Referenced by operator>>(), and animal::HistoryV< Position, Velocity >::read(). |
|
||||||||||||||||
|
Definition at line 94 of file vectorVec.h. |
|
|
Definition at line 180 of file linearX3DTK.h. References v_dot(). |
|
||||||||||||||||
|
to put a vector in an output stream
Definition at line 101 of file io.h. Referenced by operator<<(), animal::FrprMinimizer< ValueFunction, GradientFunction, Parameter, Real >::printFunction(), and animal::HistoryV< Position, Velocity >::write(). |
|
||||||||||||||||
|
Definition at line 174 of file linearX3DTK.h. |
|
||||||||||||
|
Definition at line 168 of file linearX3DTK.h. |
|
||||||||||||||||||||
|
Definition at line 83 of file vectorVec.h. |
|
||||||||||||||||
|
Add derivatives component-wise.
Definition at line 296 of file integrator.h. References animal::Derivs< Vels, Accs >::accelerations, v_peq(), and animal::Derivs< Vels, Accs >::velocities. |
|
||||||||||||||||
|
||||||||||||||||
|
Definition at line 105 of file vectorVec.h. |
|
||||||||||||||||
|
||||||||||||||||
|
Write the rotation matrix m corresponding to quaternion q, in OpenGL format (the rotation matrix is transposed); Assumes that the quaternion is normalized Definition at line 1102 of file quaternion.h. References animal::Quaternion< RealT, TraitsT >::w(), animal::Quaternion< RealT, TraitsT >::x(), animal::Quaternion< RealT, TraitsT >::y(), and animal::Quaternion< RealT, TraitsT >::z(). |
|
||||||||||||||||
|
Write the rotation matrix m corresponding to quaternion q; Assumes that the quaternion is normalized
Definition at line 985 of file quaternion.h. References animal::Quaternion< RealT, TraitsT >::w(), animal::Quaternion< RealT, TraitsT >::x(), animal::Quaternion< RealT, TraitsT >::y(), and animal::Quaternion< RealT, TraitsT >::z(). |
 1.3.6
1.3.6