- 4.1.1 Contexte
- 4.1.2 Trois niveaux de détail
- 4.1.3 Transition
- 4.1.4 Fonctions d'animation
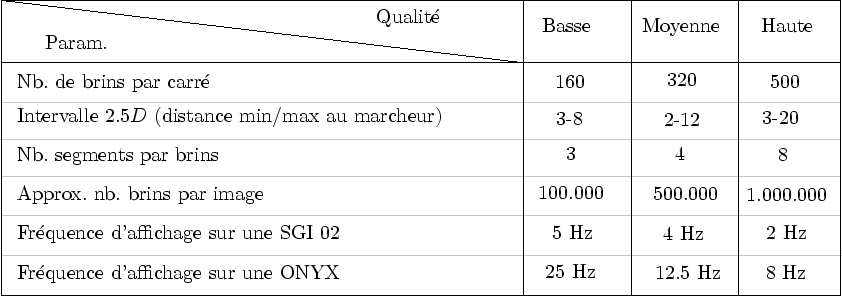
- 4.1.5 Résultats
- 4.1.6 Limitations
Je vais présenter ici un algorithme permettant le rendu et l'animation de prairies animées sous le vent. Ce travail est un cas typique de modélisation par complexification (cf. chapitre précédent). Sa description nous aidera à mieux comprendre l'intérêt de l'outil générique pour la modélisation par complexification décrit dans les chapitres suivants.
Une seconde version de l'algorithme des prairies a été implémentée par Sylvain Guerraz, François Faure et moi. Les différences avec la première en disent long sur l'art et la manière de bien aborder la modélisation par complexification. Ce chapitre est donc composé de deux sections :
Durant la première partie de ma thèse, j'ai terminé la mise au point d'un algorithme de rendu de prairies animées en temps-réel conçu pendant mon DEA [PC01].
Nous présenterons d'abord le contexte scientifique. Nous décrirons ensuite les trois niveaux de détail utilisés, puis la méthode d'animation et enfin les transitions entre niveaux de détail. Cette section se termine par une analyse critique des résultats.
Visuellement, le cerveau humain semble avoir un besoin insatiable de complexité. Ceci est particulièrement vrai quand on regarde les images synthétisées par ordinateur : les détails (si possibles animés) sont essentiels pour s'immerger dans un monde virtuel.
Mais cette complexité est difficilement réalisable dans le cadre d'applications interactives comme les jeux vidéos4.1. Grâce à la puissance des cartes graphiques et à la simplicité et le statisme de la géométrie des environnements artificiel (i.e. réalisé par l'Homme), les scènes d'intérieurs sont rendues en temps-réel avec une bonne qualité. A l'extérieur, les modèles actuels sont généralement moins séduisants, spécialement pour les scènes naturelles. En effet, la richesse de ces dernières est limitée, et elles sont très difficilement animables en temps-réel.
De plus, comme on l'a vu dans le chapitre précédent, les travaux qui vont dans cette direction sont rares. Le travail présenté ici est parmi les tous premiers à relever ce nouveau et très excitant défi. Nous proposons un algorithme permettant le rendu et l'animation d'une prairie. Les applications visées sont les jeux vidéos, c'est pourquoi le modèle a été conçu pour être observé par un marcheur parcourant la prairie (le cas général étant, comme nous le verrons, plus délicat).
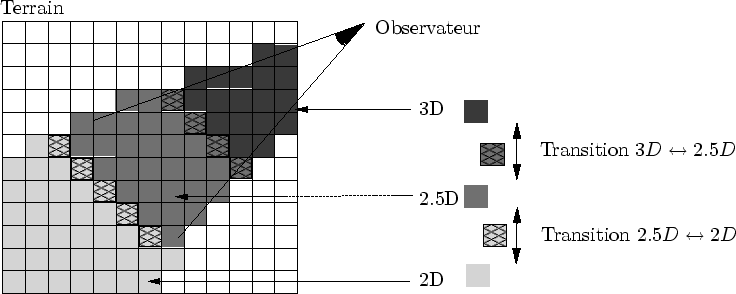
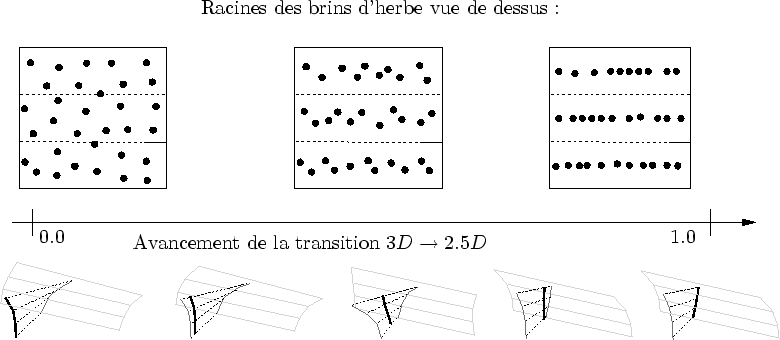
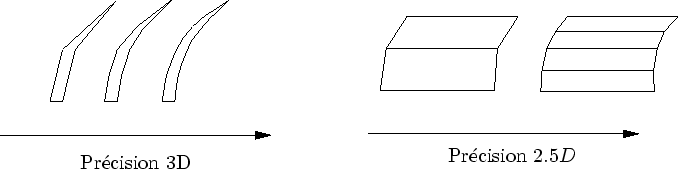
Afficher chaque brin d'herbe individuellement anéantirait tout espoir d'interactivité. Comme expliqué au chapitre 2, les méthodes de simplification sont inefficaces devant une géométrie si complexe et animée. Nous avons vu dans le chapitre 3 que les scènes complexes sont mieux représentées par des niveaux de détails de nature différentes (cf. sous-section 3.1.3). Notre solution s'appuie sur l'utilisation simultanée de trois représentations : de la géométrie 3D, des textures volumiques et des textures 2D (cf. figure 4.1).
Pour assurer des performances constantes, lors de mouvements de la caméra, certaines zones de la prairie passent d'un niveau de détail à l'autre. Afin d'éviter toute discontinuité nuisible à la qualité de l'affichage, des fonctions de transitions permettent de passer continûment d'un niveau de détail à l'autre sans altérer la qualité du rendu.
Les fonctions d'animation que nous utilisons dans notre travail puisent leur inspiration dans trois travaux :
Nous avons choisi d'animer la prairie par des primitives de vent, plus généralement appelées fonction d'animation. Elles envoient à chaque instance de chaque niveau de détail une information de mouvement procédural. Elles offrent un contrôle interactif à l'utilisateur.
Sont décrits ici les modèles géométriques utilisés pour représenter l'herbe. Trois niveaux de détail sont utilisés. Bien que, par soucis de clarté, la modélisation du mouvement sera décrite plus tard, il est important de signaler que c'est durant la modélisation géométrique que les paramètres utiles à l'animation doivent être considérés.
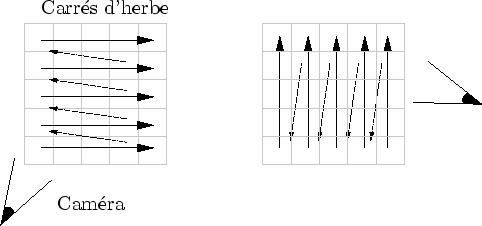
Le terrain est une carte de hauteurs et peut donc être divisé en petits carrés de terrain. Un carré est rempli d'herbe : on parlera dans la suite de carrés d'herbe. Un certain nombre de carrés d'herbe est précalculé : la position des brins d'herbes, leur taille et leur couleur sont connues à l'avance. En précalculant 2 ou 3 carrés d'herbe, en les plaçant et en les tournant aléatoirement, la répétition n'est pas visible (cf. figure 4.2).
 |
Les carrés d'herbes, selon leur distance à la caméra, utilisent différentes représentations alternatives de l'herbe. Lorsque la caméra bouge, certains carrés d'herbe passent d'une représentation à une autre et subissent une transition. Trois représentations alternatives sont utilisées. Un carré d'herbe est ignoré s'il ne se trouve pas dans le champ de vision (cf. figure 4.3).
 |
Chaque brin d'herbe est représenté par une chaîne de lignes (GL_LINES) dont la l'épaisseur varie en fonction de la hauteur.
Le brin est illuminé procéduralement : une couleur verte lui est attribuée (variant plus ou moins au hasard). La couleur est plus foncée à la base du brin afin de rendre compte (tout à fait empiriquement) du fait que moins de lumière parvient au sol. Cette représentation est la seule qui décrit la forme d'un brin d'herbe individuellement par des primitives 3D, c'est pourquoi elle est appelée la représentation 3D (cf. figure 4.1).
 |
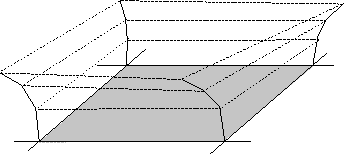
Lorsqu'un carré d'herbe est plus loin, il devient trop coûteux de dessiner chaque brin d'herbe. Le carré d'herbe est alors découpé en tranches horizontales (cf. figure 4.1). Des bandes de polygones semi-transparents subdivisent chacune de ces tranches. Ces polygones semi-transparent sont texturés avec une image RGBA (cf. figure 4.4). Le canal Alpha code la transparence. Chaque tranche est plantée verticalement parallèlement au côté du carré qui qui fait le plus face à la caméra.
La transparence est permise grâce à l'utilisation de la fonction glBlendFunc. Cette fonction est un peu capricieuse et requiert un tri des polygones semi-transparents de l'avant vers l'arrière. Compte tenu de la structure régulière du terrain, ce tri est réalisable via un simple parcours intelligent, prenant en compte la position de la caméra (cf. figure 4.5).
 |
Ce niveau de détail, compte tenu de sa construction en tranches, offre une bonne qualité de rendu lorsque l'observateur regarde la prairie d'un angle rasant (comme un marcheur). L'approximation d'un volume 3D à base de tranches de texture 2D nous a amené à appeler, très informellement, cette représentation 2.5D.
La représentation utilisée ici est une texture représentant de l'herbe directement appliquée sur le sol, c'est pourquoi elle a été nommé 2D (cf. figure 4.1). Quelques textures de cette représentation sont créés par un rendu en projection orthogonale d'un carré d'herbe 3D quelconque (cf. figure 4.6).
En fait, cette texture est légèrement surélevée et semi-transparente afin que l'on puisse distinguer la couleur du sol. Elle est aussi légèrement inclinée et montre la plus forte pente à la caméra. De cette façon, on approxime mieux le volume que devrait occuper l'herbe.
 |
Une attention particulière a été portée sur la continuité des transitions.
En effet, le marcheur (portant la caméra) va se déplacer dans la prairie.
Des transitions entre niveaux de détail doivent être déclenchées pour que la qualité visuelle et le coût d'affichage ne soient jamais dégradés.
Nous considérons que les discontinuités visuelles durant le passage d'un niveau de détail à un autre nuisent énormément au confort visuel.
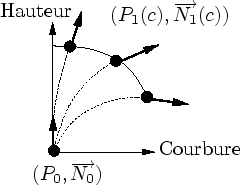
Les transitions mises en ![]() uvre entre chaque niveau sont donc des métamorphoses continues d'un niveau à l'autre.
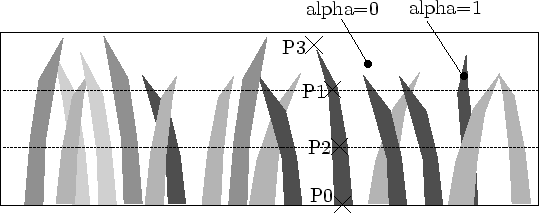
L'état de complexion d'une transition se mesure par son avancement qui n'est rien d'autre qu'un coefficient d'interpolation.
uvre entre chaque niveau sont donc des métamorphoses continues d'un niveau à l'autre.
L'état de complexion d'une transition se mesure par son avancement qui n'est rien d'autre qu'un coefficient d'interpolation.
En plus de cette continuité temporelle, les transitions 3D
![]() 2.5D assurent aussi une continuité ``spatiale'' : chaque brin d'herbe sur la texture a un homologue 3D (cf. figure 4.4).
Nous verrons comment la construction des carrés d'herbe permet cette correspondance, puis nous décrirons les transitions.
2.5D assurent aussi une continuité ``spatiale'' : chaque brin d'herbe sur la texture a un homologue 3D (cf. figure 4.4).
Nous verrons comment la construction des carrés d'herbe permet cette correspondance, puis nous décrirons les transitions.
Chaque brin d'herbe dans une texture 2.5D a un homologue 3D. Il est imaginable d'assurer cette correspondance en construisant, pour chaque carré d'herbe, autant de textures que nécessaire. Mais cela mènerait très vite à un coût mémoire exorbitant.
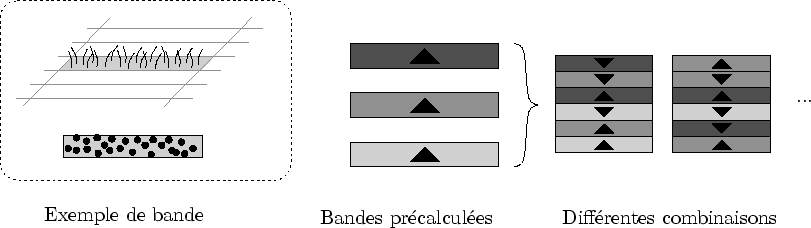 |
Lors d'une phase de précalcul, un certain nombre de tranches d'herbe sont générées. Chaque tranche d'herbe contient un ensemble de brins d'herbe dont les caractéristiques sont tirées au hasard : taille, couleur, position de racine et la courbure.
Les textures utilisées pour la représentation 2.5D sont chacune générées à partir de l'une de ces tranches précalculées (cf. figure 4.6). Ces textures sont obtenues par un rendu offscreen de la tranche correspondante avec une caméra orthogonale. Chaque carré d'herbe précalculé est alors constitué de tranches placées aléatoirement (cf. figure 4.7).
Ainsi, avec peu de textures (i.e. de tranches d'herbe), il est possible de générer combinatoirement un grand nombre de carrés d'herbe différents. La correspondance des brins d'herbe un à un est assurée par construction de la façon suivante. Un certain nombre de texture sont initialement générées au début du programme. Les tranches d'herbe sont ensuite générées à partir de ces textures.
Lorsqu'un carré d'herbe bascule du premier niveau vers le deuxième, chaque brin d'herbe 3D rejoint son homologue dans les textures 2.5D (cf. figure 4.8).
Ceci est réalisé par une simple interpolation du brin durant son mouvement (ce dernier sera décrit en 4.1.4).
En particulier, le brin d'herbe glisse sur le sol pour épouser sa nouvelle forme.
Ce mouvement est invisible pour un ![]() il non averti car il a lieu à distance suffisante.
il non averti car il a lieu à distance suffisante.
Lorsque l'interpolation est terminée, il faut ``sauter'' d'une représentation à l'autre. Ce passage ne peut pas être réalisé de façon totalement discontinue. En effet, compte tenu des représentations différentes (texture et géométrie), il existe toujours une différence visuelle non négligeable entre les deux niveaux. Pour éviter tout artefact, un fondu enchaîné est réalisé4.2.
Remarquons que les distances où ont lieu les transitions sont déterminées de façon complètement empiriques. En effet, il nous a semblé préférable, plutôt que d'établir un espace de mesure à la norme discutable, de laisser le maximum de degrés de liberté dans le paramétrage des transitions. Ces degrés de liberté étant modifiés à la volée, la phase de calibration est très rapide. Les critères de calibration sont tout simplement la qualité du rendu, en éternelle opposition avec les performances.
 |
Pour basculer de la représentation 2.5D à la représentation 2D, les textures 2.5D s'enfonce dans le sol pendant que la représentation 2D pousse (cf. figure 4.9). Aucune association de brin d'herbe n'est assurée, mais à la distance où intervient cette transition, il n'est de toute façon pas possible de distinguer un brin d'herbe individuellement.
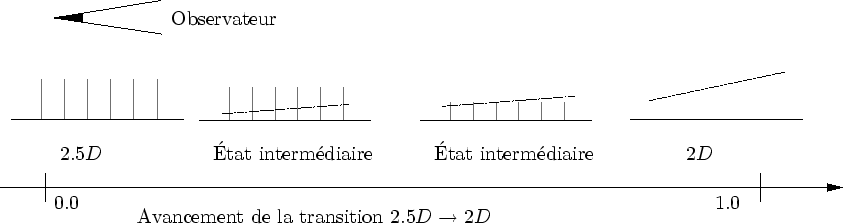 |
L'avancement des transitions ne dépendait initialement que de la position de la caméra. En conséquence, pour certaines positions de la caméra, l'avancement d'une transition pouvait rester à mi-chemin entre un niveau de détail et le suivant. Ces positions intermédiaires ne sont pas souhaitables pour la simple raison qu'elles sont plus coûteuses qu'un niveau déterminé et offrent une moindre qualité de rendu. En effet, les états transitoires n'existent que pour assurer la continuité et l'esthétisme est maximal aux états ``de repos'' (sans transition).
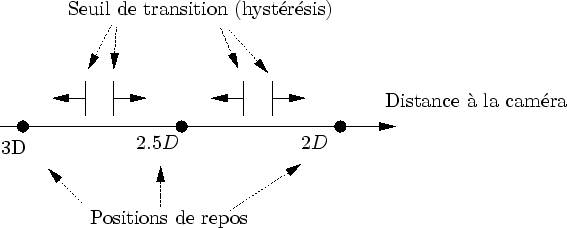
Ceci a tout naturellement mené à des transitions asynchrones qui, une fois déclenchées, évoluent inexorablement jusqu'à leur complexion. Pour limiter les problèmes d'oscillations entre des différents niveaux de détail, des seuils de déclenchements différents sont utilisés d'un niveau à l'autre (cf. figure 4.10). Cette technique est appelé transition par hystérésis par [LRC+02].
 |
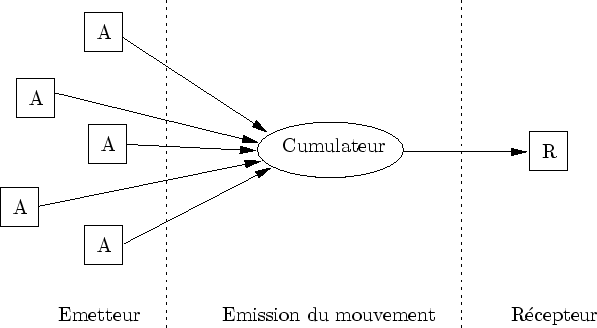
Avant de décrire la méthode d'animation et de donner quelques exemples, il est nécessaire de décrire les degrés de liberté que proposent les trois représentations. L'animation de la prairie reviendra à modéliser l'action des ``primitives de vent'' sur ces degrés de liberté.
L'animation consiste à simuler la courbure que subit un brin d'herbe dans une direction donnée sous l'action du vent. Afin de permettre cette action, les différentes représentations offrent un certain nombre de degrés de liberté:
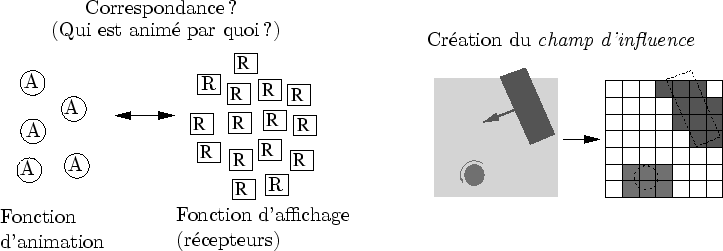
L'ensemble des paramètres de chaque instance d'un niveau de détail est appelé un récepteur : c'est lui qui reçoit l'information envoyée par les primitives de vent.
Des fonctions d'animation, ou primitives de vent, modifient la prairie en simulant différents types de vent tels que des bourrasques, une brise légère ou un tourbillon (cf. figure 4.12). Pour de bonnes performances, plutôt que de simuler le vent comme un fluide et de déterminer son action sur chaque brin d'herbe, les fonctions d'animation modélisent directement l'action du vent sur l'herbe.
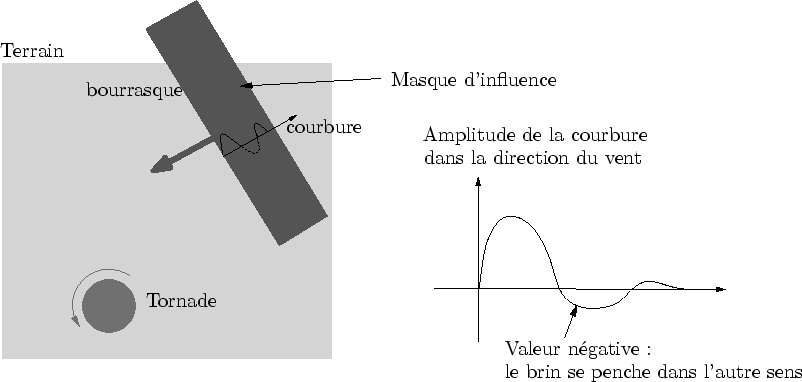 |
Ces fonctions ne s'appliquent pas à tous les brins d'herbes mais seulement à ceux compris dans un certain masque d'influence. chaque primitives de vent a son propre masque d'influence représenté par une forme géométrique 2D simple. A chaque pas de temps, tous les carrés d'herbe visibles de la prairie détectent quelles sont les primitives de vent susceptibles de les influencer en calculant leur intersection avec le masque de chaque primitive (cf. figure 4.13).
 |
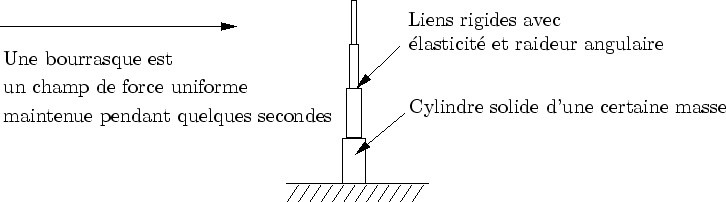
Une bourrasque est définie par un masque d'influence rectangulaire qui avance sur la prairie (cf. figure 4.12) dans une certaine direction principale. Chaque brin d'herbe (ou brin directeurs) influencé se courbe dans la direction principale et oscille jusqu'à revenir à sa position de repos Il est possible de déclencher une bourrasque de vent sur commande.
Les positions possibles d'un brin d'herbe soumis à une bourrasque sont précalculées dans un tableau de positions indexées par la courbure. Il est envisageable de calculer ces positions à l'aide d'un programme de simulation physique. Nous avons utilisé le programme ABDULA, réalisé par François Faure [Fau99] (cf. figure 4.14).
La brise est modélisée par un petit mouvement aléatoire qui influence toute la prairie.
L'amplitude évolue selon la formule
![]() .
Pour chaque brin d'herbe, la valeur de
.
Pour chaque brin d'herbe, la valeur de ![]() évolue lentement et aléatoirement afin que le mouvement ne ressemble pas à celui d'un métronome.
De même, la valeur de
évolue lentement et aléatoirement afin que le mouvement ne ressemble pas à celui d'un métronome.
De même, la valeur de ![]() (l'amplitude maximale) évolue pour briser toute sensation de répétitivité.
(l'amplitude maximale) évolue pour briser toute sensation de répétitivité.
 |
D'autres primitives ont été modélisées : une tornade, les mouvements induis par un hélicoptère... Grâce à leur nature procédurale, il est très facile de rajouter de nouvelles primitives de vent. Néanmoins, la principale limitation de notre algorithme réside en la manière dont sont combinées les fonctions d'animation.
En pratique, plusieurs primitives de vents peuvent être activées en même temps sur la prairie et passée sur les mêmes endroits. Nous les combinons de façon très simple en leur donnant une priorité. La primitive de vent qui a la plus haute priorité annule les influences des autres primitives. Par exemple, une tornade annulera les effets d'une bourrasque qui annulera les effets de la brise légère.
Nous avons présenté une solution au problème des prairies animées sous le vent. Ce travail à fait l'objet d'une publication à Interactive 3D Graphics [PC01].
 |
Le coefficient
![]() de notre système dépend de nombreux paramètres :
de notre système dépend de nombreux paramètres :
L'utilisation de trois représentations de nature différente est bien entendu le point clef de ce travail. Elle illustre parfaitement la ``loi du cas particulier'' exposé en 3.3 : des choix adaptés à un phénomène particulier s'avère bien plus souple et efficace que des algorithmes universels. La gestion combinée de différentes représentations, d'animation procédurale et des transitions continues montrent une nouvelle voie dans la modélisation multi-échelle : la complexification (cf. chapitre 3).
L'animation, dans son extrême simplicité, est pourtant la grande force du programme (cf. figure 4.16).
En effet, cette vaste étendue d'herbe se déplaçant plus ou moins harmonieusement est du meilleur effet sur l'![]() il humain.
L'aspect des brins d'herbe, bien que simplifié à l'extrême, reste crédible.
C'est la preuve que l'Homme, dans certains cas, n'a pas besoin d'un réalisme très poussé pour se laisser convaincre.
il humain.
L'aspect des brins d'herbe, bien que simplifié à l'extrême, reste crédible.
C'est la preuve que l'Homme, dans certains cas, n'a pas besoin d'un réalisme très poussé pour se laisser convaincre.
Ce premier résultat soulève des questions d'ordre perceptuel. Était-il possible de prévoir que l'emploi des trois niveaux de détails et des fonctions d'animation donnerait d'aussi bons résultats ? La réponse me semble être négative. La méthode utilisée ne supporte pas de mesure de qualité a priori pour la simple raison que l'espace dans lequel une telle mesure prendrait effet n'existe pas avant la création du modèle (ou du moins, il est beaucoup trop complexe). Contrairement à de nombreuses méthodes, on doit créer l'espace de mesure avant d'espérer en tirer quoique ce soit. Cette approche, comme tout notre programme, est extrêmement empirique.
Insistons sur l'aspect pseudo-chaotique de la prairie : c'est lui qui, malgré l'irréalisme du modèle, trompe l'![]() il humain.
Nous sommes en effet exceptionnellement doués pour détecter la répétitivité, qu'elle soit spatiale ou temporelle.
Toute monotonie détériore l'esthétique d'une scène.
il humain.
Nous sommes en effet exceptionnellement doués pour détecter la répétitivité, qu'elle soit spatiale ou temporelle.
Toute monotonie détériore l'esthétique d'une scène.
Des fonctions aléatoires aux lois bien choisies sont utilisées à de nombreux endroits : la couleur, la direction par défaut, l'amplitude maximum, la répartition, la taille... Chaque brin d'herbe est d'une certaine façon unique. Les fonctions d'animation sont aussi ``randomisées'' dans leur vitesse et leur placement.
Plus généralement, le bon usage de fonctions aléatoires est un facteur essentiel à la qualité de tout modèle procédural décrivant des scènes naturelles.
 |
La méthode de combinaison des différentes influences des primitives de vent est insuffisante. Une simple priorité ne peut pas, par exemple, tenir compte de l'effet cumulé de différentes primitives.
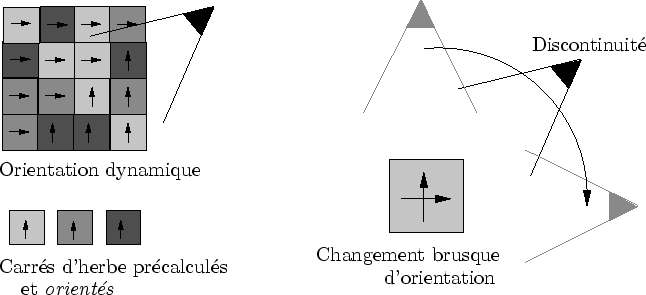
La figure 4.2 a été simplifié : les carré d'herbes sont en fait orientés. La détermination de leur orientation à la volée peut parfois entraîner une discontinuité dans la représentation (cf. figure 4.17). Utiliser un simple fondu enchaîné pour remédier à cette discontinuité de l'affichage n'est pas évident compte tenu de la géométrie entre-croisée. En effet, pour trier les polygones (nécessaire pour un rendu avec transparence), il faudrait décomposer chaque polygone semi-transparent. Nous verrons dans la section 4.2 comment ce problème a été corrigé.
 |
La densité de l'herbe est quasi-constante sur tout le terrain. Il est possible de décréter que certains carrés d'herbe sont en fait désertiques, mais l'effet ne serait pas convaincant car la prairie serait comme crénelée. Une densité variant continûment est nécessaire si on veut représenter un paysage plus réaliste. Malheureusement, les textures précalculées engendrent une contrainte très forte : il doit y avoir autant de brins d'herbe dans une tranche que dans la texture associée. Il est envisageable de construire plusieurs types de texture correspondant à des densités différentes. La difficulté viendrait ensuite de leur assemblage.
Seul un angle de vue rasant offre une bonne qualité de rendu. Ceci est dû aux niveau 2.5D et 2D qui sont prévus pour être observés d'un angle bien particulier. Cette limitation est sans-doute la plus nuisible. Même si l'on restreint l'observateur à un marcheur (disons 2 mètres au dessus de la prairie), cela ne l'empêchera pas de voir des portions de prairie avec un angle de vue important si le terrain est très dénivelé (cf. figure 4.18). Ainsi, pour assurer une bonne qualité de rendu, non seulement on doit contraindre l'observateur à l'état de marcheur, mais il est aussi nécessaire de limiter la taille des bosses du terrain... Ces contraintes deviennent vite très restrictives.
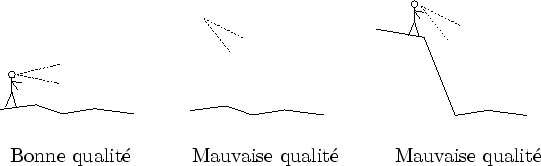 |
La première version des prairies a donné suite à une nouvelle mouture principalement développée par Sylvain Guerraz [GPR+03] lors de son stage de magistère. J'ai participé à l'encadrement, principalement effectué par François Faure. Les différentes représentations et leurs animations restent sensiblement les mêmes. En revanche, la flexibilité du modèle a été améliorée, permettant de repousser certaines limitations inhérentes à la première version.
L'utilisation de tableaux de position, utilisés dans la première version, limite la variété des mouvements (cf. sous-section 4.1.2). L'apparence d'un brin d'herbe étant simple et variant peu, il est facile de générer ce dernier à la volée sans jamais stocker sa géométrie. La courbe d'un brin d'herbe est donc calculée grâce à une simple courbe de Hermite.
Il faut cependant faire attention à conserver approximativement la taille du brin d'herbe pour n'importe quelle paramétrisation (tout droit, courbé, couché). Les fonctions permettant de conserver la longueur d'une courbe sont rares et coûteuses. Par soucis d'efficacité, une taille à peu près constante est assurée par une fonction de ``rapetissage'' (cf. figure 4.19).
 |
Les textures utilisées sont désormais paramétrées par un facteur alpha. Celui-ci, grâce à l'utilisation du GL_ALPHA_TEST, permet d'afficher plus ou moins de brins d'herbe, selon la valeur du seuil alpha (cf. figure 4.20). Ce système a été utilisé avec succès pour les textures 2D et 2.5D. Il permet, grâce à une carte de densité, d'obtenir des terrains dont la répartition d'herbe est très variable (cf. figure 4.24).
C'est donc en ajoutant un degré de liberté dans le rendu des textures qu'il a été possible de varier la densité. L'ajout de ce degré de liberté est réalisé au détriment de l'association des brins d'herbe 3D et 2.5D. Cela signifie que lors d'une transition entre ces deux représentations, la correspondance des brins d'herbe n'est plus assurée.
Ce choix allège énormément la conception des transitions : il n'est plus nécessaire de garder les coordonnées des brins d'herbe dessinés dans les textures (cf. figure 4.4). Cette perte entraîne une légère dégradation du rendu : durant le déplaçant de l'observateur, l'observateur attentif distingue une onde de discontinuité au niveau des transitions entre la 3D et la 2.5D. Même si cela s'annonce délicat, il semble possible de conserver la correspondance des brins d'herbe tout en gardant un paramétrage de la densité. Affaire à suivre...
Afin de remédier au problème de ``l'observation rotative'', les polygones texturés entourent les carrés d'herbe (cf. figure 4.21). De cette façon, la géométrie ne dépend moins de l'angle d'observation. Pour une qualité similaire, le nombre de polygones utilisé est très légèrement supérieur. En effet, l'orientation est moins optimisée pour l'observateur. En revanche, la caméra peut maintenant se déplacer sans contrainte dans la prairie, sans soulever le problème des ``l'observation rotative'' évoqué plus haut.
 |
Au sein d'un même niveau de détail, la géométrie est échantillonnée plus ou moins finement selon la distance à la caméra (cf. figure 4.22).
Cela permet une meilleure adaptation de la précision et ainsi un meilleur
![]() .
.
 |
Un effort a aussi été porté sur les fonctions d'animation.
Tout d'abord, un moteur d'animation procédurale a été développé. Il gère la vie des fonctions d'animation. Son rôle est le suivant :
 |
Une fonction d'animation d'écrasement d'herbe a été ajoutée. Elle permet de simuler procéduralement l'herbe écrasée (par un personnage par exemple) en la couchant temporairement sur le sol (cf. figure 4.24). Pour plus d'informations sur cette fonction, référez vous à [GPR+03].
 |
Nous décrirons d'abord quelques améliorations qu'il serait souhaitable d'ajouter à la seconde version des prairies. Nous décrirons ensuite en quoi ces travaux sont une expression du besoin d'un modeleur par complexification (qui fait l'objet du chapitre 5).
La prairie dans sa version actuelle est efficace et simple à utiliser. Elle a été combinée à une technique d'animation d'arbres dans [GCF01]. Il est envisageable de l'intégrer à un moteur de rendu dédié au jeu. Pourtant, il reste quelques point à éclaircir.
De nombreuses contraintes sont posées sur l'observateur. Celui-ci doit observer la prairie ni de trop loin (pas plus de quelques centaines de mètre), ni de trop près (pas à moins de un mètre). De plus, notre marcheur ne peut pas observer la prairie d'en haut. Ce sont beaucoup de limites pour de la recherche qui se proclame multi-échelle et il est clair qu'ici, beaucoup reste à faire.
Notons néanmoins que ces limites existent forcément quelque soit le modèle. A l'exception des fractals (malheureusement très peu variées), il n'existe pas de modèles permettant n'importe quelle échelle d'observation. En fait, il serait peut-être souhaitable de mieux préciser les plages d'observation valide de chaque modèles multi-échelle. Une telle mesure permettrait de placer chaque modèle sur un puzzle pour modéliser des phénomènes de plus en plus grand sur des échelles variants toujours plus.
Toutes ces prairies manquent de fleurs : une plus grande variété de végétation améliorerait beaucoup la qualité du rendu. Pour cela, une très grande cohérence entre la géométrie et les textures devra être assuré. En effet, il n'est pas question de faire apparaître et disparaître de gros pétales rouges lors d'une transition.
Les textures ont la fâcheuse tendance d'être très peu paramétrables et en conséquence très statiques.
Les problèmes de variété et de densité en sont des conséquences directes.
La solution mise en ![]() uvre pour améliorer le contrôle sur la densité consiste justement à paramétrer la texture avec le canal alpha.
uvre pour améliorer le contrôle sur la densité consiste justement à paramétrer la texture avec le canal alpha.
De nombreuses méthodes proposent de générer des textures procédurales. Notamment, la programmabilité des cartes graphiques, même embryonnaire, permet de plus en plus de souplesse. Les textures pourront bientôt être composées de sous-textures, engendrées par des fonctions mathématiques simples, des fonctions de bruits... En bref, les textures procédurales ont de beaux jours devant elles. Leur utilisation pour la prairie est très prometteuse.
Les difficultés rencontrées durant le développement de la prairie sont la motivation initiale d'un outil générique pour la modélisation procédurale multi-échelle.
Tout d'abord, la prairie, que ce soit dans la première ou la seconde version, est bien un exemple de modélisation par complexification. Cela peut ne pas paraître évident compte tenu du fait qu'elle n'a pas été présentée de son niveau le plus grossier vers le niveau le plus fin. Pourtant, la diversité des représentations utilisées, la complexité du langage descriptif (le C++) et la quantité très faible de précalculs pour la version finalement retenue sont des signes qui ne trompent pas.
Remarquons que durant la conception de la première version, toute la structure de la prairie reposait sur des précalculs lourds (chaque brin d'herbe de la prairie existait à son niveau le plus fin). Cela n'a pas été évident d'assouplir ces précalculs pour quitter doucement la simplification et se rapprocher de la complexification. Cependant, la complexité du modèle et de son animation n'offrait pas d'autre choix que d'aller dans cette direction. La seconde version de la prairie est d'ailleurs un pas de plus vers la complexification.
Lors de la modélisation de la prairie, le temps passé à améliorer son esthétisme a été quasiment nul ! En un sens, ceci est rassurant : je ne suis pas un artiste. Dans le cadre de ma thèse, mon rôle n'est pas de réaliser de belles choses, mais de proposer des moyens pour y arriver.
Néanmoins, la question se pose : où est la difficulté?
En fait, les seuls représentants du temps passé spécifiquement sur la prairie sont les transitions (ce qui est normal, compte tenu de ce qui a était dit en 3.1).
En somme, disons que ![]() du temps qui a été nécessaire à la réalisation des prairies a directement servi ce but.
C'est peu.
du temps qui a été nécessaire à la réalisation des prairies a directement servi ce but.
C'est peu.
La première version a été développée en six mois par une personne. La seconde version a profité de l'expérience acquise durant la première ainsi que du moteur d'animation procédurale. Pour des résultats bien meilleurs, cette dernière a été implémentée en trois mois par un stagiaire niveau maîtrise et comprend une interface graphique dédiée (cf. figure 4.25). Remarquons que l'utilisation de transitions n'assurant pas la correspondance des brins d'herbe un à un a notablement allégé la modélisation. En revanche, la mise en commun des arbres et de la prairie pour [GPR+03] a demandé une certaine énergie.
 |
La prairie, comme toutes les réalisations procédurales multi-échelles, a un besoin crucial d'un environnement de modélisation. La plupart des critères énumérés dans 3.3.4 sont ici valides :
De façon moins évidente :
Le dernier point non abordé est celui de la cohérence temporelle. La première version de la prairie est basée sur une information dynamique mise à jour à chaque pas de temps : les carrés d'herbe visibles restent en mémoire de façon permanente. Dans la seconde version, la génération des brins d'herbe est réalisée à la volée (cf. sous-section 4.2.1), sans aucune mémoire de l'état précédent. Certaines fonctions d'animation nécessitant la connaissance de cet état, il n'a pas été évident de rendre permanentes certaines données (c'est en fait le moteur d'animation qui assure cette permanence). Ici, une bonne gestion de la durée de vie de l'information aurait été très utile.
La réalisation des prairies animées est la première étape d'une pensée qui, me semble-t-il aujourd'hui, ne pouvait aboutir que dans la réalisation de Dynamic Graph.