Modélisation multi-échelle procédurale de scènes animées
Frank Perbet - 2004/04/25

Next: 6. Dynamic Graph : Up: main Previous: 4. Étude de cas

5. Dynamic Graph : un outil générique pour la modélisation multi-échelle

Ce chapitre propose une vue d'ensemble de Dynamic Graph, un outil de modélisation par complexification générique que j'ai conçu et développé durant ma thèse. Il introduit les chapitres suivants :

le chapitre 6 détaille le coeur de Dynamic Graph, c'est-à-dire les mécanismes nécessaires à l'évaluation et l'affichage du modèle ;
le chapitre 7 prend le point de vue du créateur et décrit l'acte de modélisation ainsi que les résultats obtenus.

Voici un survol des différentes sections de ce chapitre.

Introduction à Dynamic Graph:: Bien que la prairie n'ait pas été réalisée avec Dynamic Graph, elle est une transition idéale qui reflète parfaitement le cheminement de ma pensée. Ce chapitre débute donc par la description du modèle de prairie tel qu'il aurait été réalisé avec Dynamic Graph. Cela permettra d'introduire le langage descriptif de Dynamic Graph basé sur un nouveau concept : les amplifieurs.
Évaluation du modèle:: Après cette introduction à Dynamic Graph, nous donnerons un premier aperçu des mécanismes complexes qui assurent la transformation du modèle décrit par le créateur en pixel sur l'écran. Cette transformation est appelée évaluation. Notez que dans tout ce document, le terme évaluation doit être compris comme un synonyme de calcul (et non de validation).
Bilan intermédiaire:: la section 5.3 fait un bilan de ce chapitre et introduit le contenu des chapitres 6 et 7.

5.1 Introduction à Dynamic Graph

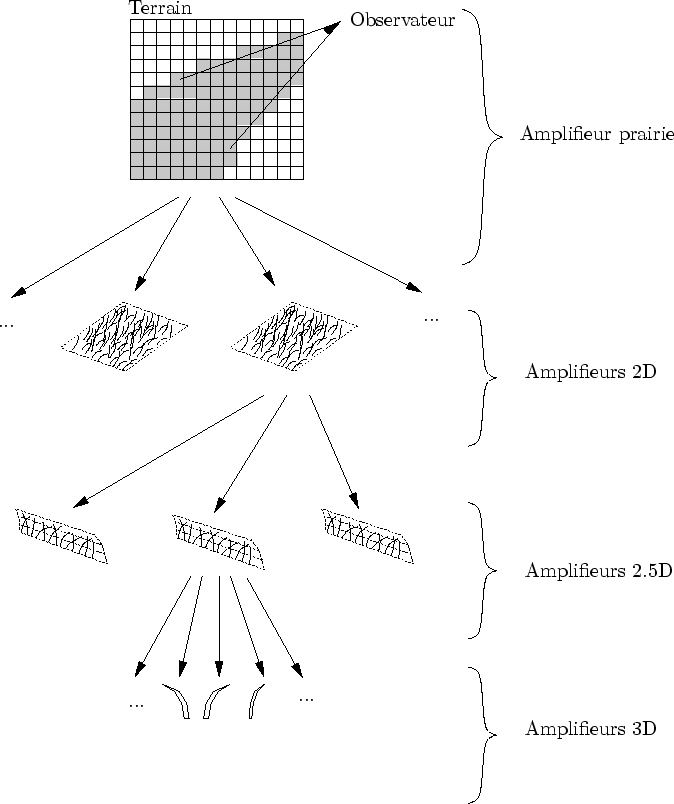
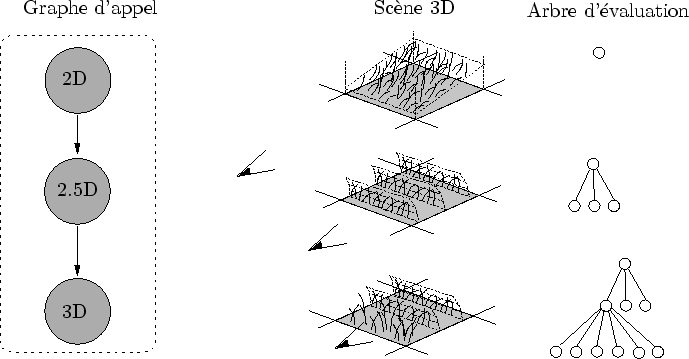
La prairie, décrite au chapitre précédent, est ici reformulée avec le langage descriptif que propose Dynamic Graph. Cette section propose donc une entrée en matière basée sur cet exemple^5.1. Nous verrons tout d'abord comment voir la prairie comme une modélisation par complexification et nous introduirons le concept d'amplifieur qui est le fondement du langage descriptif de Dynamic Graph. Enfin, nous aborderons le problème complexe de la persistance d'information.

5.1.1 Vue de la complexification

Une forme visible peut être vue comme une forme grossière auquel on ajoute progressivement et localement des détails. Une fonction qui ajoute des détails est appelée un amplifieur. Une scène 3D pourrait donc être décrit par une forme grossière et un ensemble d'amplifieur. Mais Dynamic Graph va plus loin dans l'abstraction de la représentation du modèle : le créateur ne donne pas des amplifieurs, mais des générateurs d'amplifieurs. Ceux-ci ont pour fonction de créer des amplifieurs automatiquement. Voyons plus précisément la nature de ces générateurs d'amplifieurs dans le cas de la prairie.

5.1.1.1 Amplifications successives

Imaginons que la prairie soit initialement définie par une forme grossière : le carré d'herbe 2D. Celle-ci est enrichie par les représentations 2.5D et 3D en fonction de la position de la caméra (cf. figure 5.1).

Dans Dynamic Graph, la description du fonctionnement d'un niveau de détail est un générateur d'amplifieurs. Le rôle du créateur, lors de la modélisation est principalement de créer ces générateurs. Ensuite, lors d'une observation, Dynamic Graph augmente automatiquement la précision à différents endroits en créant une multitude d'amplifieurs générés par les générateurs.

Il est important de bien distinguer ces deux entités :

un amplifieur: ajoute de la précision à un certain endroit du modèle. Dans la prairie, chaque brin d'herbe et généré par un amplifieur ``3D''.
un générateur d'amplifieurs: génére automatiquement des amplifieurs. Le créateur, lorsqu'il invente un nouvel objet, le décrit par des générateurs d'amplifieurs, et non pas directement par des amplifieurs.

Le langage descriptif d'un objet décrit avec Dynamic Graph est donc essentiellement un ensemble de générateur d'amplifieurs. Cette représentation est un pas de plus dans l'abstraction d'un modèle : celui-ci est représenté non plus par les fonctions qui le construisent, mais par des fonctions qui génèrent des fonctions qui le construisent. Remarquons que cette approche très procédurale permet de mieux capturer la répétitivité d'un scène. Par exemple, dans le cas des prairies, les brins d'herbe ne sont pas modelisés un a un : un générateur d'amplifieurs crée de multiples instances d'amplifieur (qui représente chacun un brin d'herbe).

De façon très simplifiée, un amplifieur a deux fonctions possibles :

il peut afficher une partie du modèle ;
ou bien il peut déclencher des fonctions de transition pour ajouter de la précision à cette partie du modèle.

**Figure 5.1:** Un premier amplifieur ``prairie'' engendre les amplifieurs 2D à condition que ceux-ci soient dans le champ de vue. Ensuite, en fonction de la précision, les amplifieurs vont continuer leur ajout de précision (leur amplification) ou bien dessiner la forme qu'ils représentent.
$\begin{figure}\begin{center} \input{prairie_amp.pstex_t}\end{center}\end{figure}$

5.1.1.2 Ajout de précision

Un amplifieur est un objet capable de se dessiner ou bien de créer plus d'information (de s'amplifier). Les fonctions de transitions sont réalisées par la création de nouveaux amplifieurs. L'idée générale de cette reformulation est la suivante (cf. figure 5.1):

si un amplifieur 2D est suffisamment précis, il se dessine, sinon il engendre des sous-amplifieurs 2.5D ;
si un amplifieur 2.5D est suffisamment précis, il se dessine, sinon il engendre des sous-amplifieurs 3D ;
les amplifieurs 3D n'ont pas d'autre choix que de s'afficher car ils ne savent pas générer de sous-amplifieurs (aussi appelés amplifieur fils).

5.1.2 Modélisation de la prairie

Dynamic Graph propose un langage descriptif basé sur le C++ permettant la description d'une scène par un ensemble de générateurs d'amplifieurs.

5.1.2.1 Création d'un nouveau générateur d'amplifieurs

Avec Dynamic Graph, le créateur doit fournir des générateurs d'amplifieurs qui seront transformés en amplifieurs (i.e. instance de générateur d'amplifieurs) lors d'une évaluation. Très concrètement, le langage de modélisation est le C++ auquel quelques contraintes sont ajoutées. Pour chaque amplifieur, il faut remplir le corps de certaines fonctions :

constructeur:: les constructeurs sont appelés lors de nouvelles amplifications (de construction de sous-amplifieurs).;
affichage:: si la précision est suffisante, un amplifieur s'affiche ;
amplification:: si elle n'est pas suffisante, il faut enrichir la forme et continuer l'amplification par la génération de sous-amplifieurs (par des appels du constructeur).

5.1.2.2 Cas des prairies

Afin de fixer les idées, voici, pour chaque générateur d'amplifieurs, le rôle de chacune des fonctions :

générateur d'amplifieurs ``prairie'':

: constructeur : construit une prairie avec un certain pavage, un certain type d'herbe et de nombreux autres paramètres donnés par le créateur... Cet amplifieur est l'amplifieur axiome : c'est le premier a être généré. Il détermine la distance maximale d'observation : si elle est dépassé (i.e. si l'observateur s'éloigne encore), le phénomène d'aliasing par sur-échantillonement (cf. 2.1.2) du modèle apparaît ;
: affichage : affiche le terrain ;
: amplification : produit les carrés d'herbe 2D s'ils sont dans le champ de vue.

générateur d'amplifieurs 2D:

: constructeur : construit un carré d'herbe basé sur une certaine combinaison de tranches d'herbe (cf. figure 4.7) ;
: affichage : affiche la texture 2.5D (éventuellement en cours de transition) ;
: amplification : génère les amplifieurs 2.5D correspondant aux tranches d'herbe du carré.

générateur d'amplifieurs 2.5D:

: constructeur : construit une tranche d'herbe et calcule l'animation ;
: affichage : affiche les polygones semi-transparents correspondant à la tranche d'herbe (éventuellement en cours de transition) ;
: amplification : construit les brins d'herbe associés à la tranche d'herbe.

générateur d'amplifieurs 3D:

: constructeur : construit d'un brin d'herbe et calcule l'animation ;
: affichage : affiche d'un brin d'herbe (éventuellement en cours de transition) ;
: amplification : aucune amplification n'est codée. Cela détermine la distance minimale d'observation : si elle est dépassé (i.e. si l'observateur se rapproche encore), le phénomène d'aliasing par sous-échantillonement (cf. 2.1.2) du modèle apparaît.

5.1.3 Processus de création

La représentation que fournit le créateur lors de la modélisation est donc un ensemble de générateurs d'amplifieurs. Ceux-ci, durant l'évaluation, vont engendrer des amplifieurs jusqu'à satisfaire la précision requise par l'observation. Ces amplifieurs envoient finalement des commandes à la carte graphique afin d'afficher le modèle.

5.1.3.1 Outils de modélisation

Très concrètement, l'acte de modélisation se passe de la façon suivante : chaque générateur d'amplifieurs est écrit en C++ par le créateur. Différents outils d'aide au développement sont fournis et simplifient la modélisation : ils seront discutés dans le chapitre 7.

5.1.3.2 Évaluation

**Figure 5.2:** La nature du langage descriptif varie au fil de l'évaluation. Le langage descriptif initial est une sorte de C++ spécialisé pour la description de générateurs d'amplifieurs. Au fil de l'évaluation, ces classes génèrent des instances de classes, des commandes OpenGL et enfin des pixels sur l'écran.
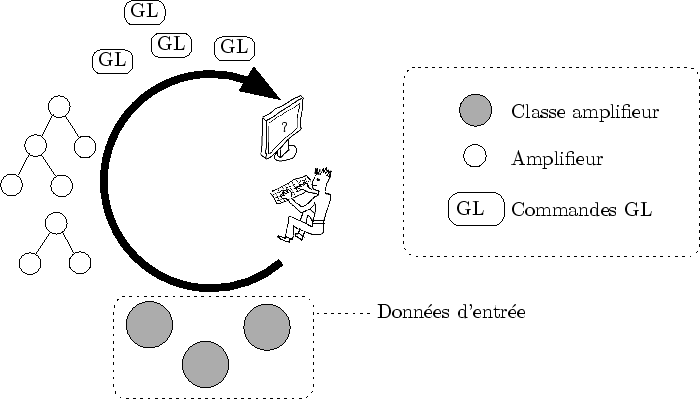$\begin{figure}\begin{center} \input{organiseur.pstex_t}\end{center}\end{figure}$

Une fois les générateurs d'amplifieurs fournis (cf. figure 5.2), la scène est évaluée ``à la volée'' en fonction de l'observation. Cette évaluation entraîne une production de nouveaux amplifieurs à partir de l'amplifieur axiome. Ils sont stockés dans un arbre appelé arbre d'évaluation. A chaque nouvelle observation (i.e. à chaque pas de temps) la scène est réévaluée et engendre un nouvel arbre d'évaluation.

5.1.3.3 Rendu

Au fil de l'évaluation, les amplifieurs envoient des commandes à la carte graphique pour dessiner le résultat final, en l'occurrence la prairie sous le vent. Des critères de précision et de visibilité sont utilisés pour n'envoyer que les commandes nécessaires.

5.2 Vue d'ensemble

Dans cette section, la partie évaluation est décrite dans son ensemble. Tout d'abord, les amplifieurs, fondement de Dynamic Graph, sont détaillés. Nous verrons ensuite comment l'observation d'une forme engendre un arbre d'évaluation. Ensuite, nous motiverons et décrirons l'organiseur, dont le but est de garder un maximum de contrôle sur la génération de l'arbre d'évaluation. Enfin, nous verrons quel support Dynamic Graph fournit pour l'animation et porterons notamment notre attention sur la mémoire nécessaire à la cohérence temporelle.

5.2.1 Amplifieurs

5.2.1.1 Fonctions paramétrables

Lors d'une modélisation avec Dynamic Graph, le créateur écrit des fonctions qui vont enrichir la forme : les générateurs d'amplifieurs. Ces derniers sont en fait des fonctions qui renvoient des fonctions :

$\begin{displaymath} u \stackrel{g}{\longmapsto} ( x \stackrel{g_u}{\longmapsto} f_u(x) ) \end{displaymath}$

Le générateur renvoie, en fonction du contexte , la fonction qui va ajouter de la précision à la forme. Le contexte représente en quelque sorte toutes les variables qui sont inconnues lors de la modélisation.

Il existe plusieurs raisons pour lesquelles une variable est inconnue :

dans Dynamic Graph, un modèle est représenté par ajout de précision successif. le contexte peut représenter la partie de la forme qui va être amplifier : il indique où et comment il faut enrichir le modèle ;
le contexte peut aussi représenter tous les événements qui sont imprévisibles lors de la modélisation tel que le déclenchement d'une bourrasque de vent par exemple.
l'observateur, ainsi que tous les paramètres influençant l'affichage, font aussi partie du contexte : la position de la caméra, le temps qui passe, la précision requise... Tous ces paramètres changeront le comportement des amplifieurs et ne sont connus que lors de l'affichage.

La modélisation proposée par le langage descriptif de Dynamic Graph impose en quelque sorte un niveau d'abstraction supplémentaire. Plutôt que d'appliquer plusieurs fois la même fonction (ou amplification) à une forme, le créateur choisit de décrire une façon automatique pour appliquer ces fonctions : les générateur d'amplifieurs. Dynamic Graph est donc d'autant plus performant que les fonctions sont répétitives.

5.2.1.2 Une représentation orientée-objet

Pour des raisons de performance, le langage C++ a été choisi comme fondement du langage descriptif. Nous discuterons des conséquences de choix dans la section 8.1. Un générateur d'amplifieurs est une classe dont chaque instance d'objet est un amplifieur . Le contexte représente principalement les paramètres du constructeur. C'est la représentation utilisée par Dynamic Graph : une forme visible est un ensemble de classes écrites dans un langage orienté-objet : le C++.

est un objet-fonction qui ajoute de la précision à la forme. Il est appelé amplifieur. La classe qui le génère est un générateur d'amplifieurs. Dans Dynamic Graph, le créateur s'exprime donc en définissant de nouveaux générateurs d'amplifieurs.

Les paramètres contenus dans , c'est-à-dire les paramètres du constructeur du générateur d'amplifieurs, font partie du contexte. Le contexte représente les données qui dépendent de l'observation (comme la position de la caméra). Lors de la modélisation, ce sont donc les ``inconnues'' dont la valeur ne sera révélée que lors d'une observation particulière.

On distingue généralement deux parties dans un objet : les variables et les fonctions. Dans Dynamic Graph, c'est la partie fonctionnelle des objets qui est la plus importante. Un objet est avant tout un ensemble de fonctions qui vont être évaluées pour répondre à une observation.

Les variables membres, c'est-à-dire la zone mémoire dynamique de l'objet, doivent être considérées comme un support des fonctions. Concrètement, elles servent la plupart du temps à stocker les résultats intermédiaires des fonctions. Le résultat final d'un amplifieur est l'affichage de la forme enrichie.

**Figure 5.3:** (a) Le créateur, durant la phase de modélisation, produit les *générateurs d'amplifieurs*. (b) Celles-ci produisent, grâce aux données fournies par l'observation, les objets *amplifieurs*. (c) Les *amplifieurs* produisent l'image.
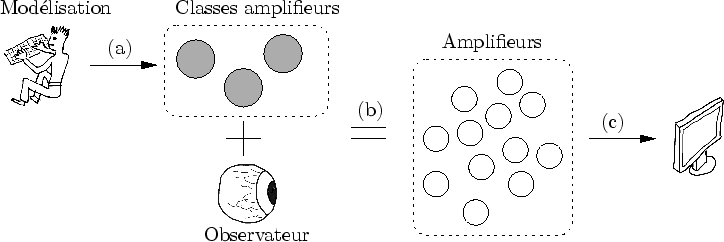$\begin{figure}\begin{center} \input{amplifieur.pstex_t}\end{center}\end{figure}$

5.2.1.3 Génération de nouveaux amplifieurs

La description d'un modèle consiste essentiellement en la donnée des générateurs amplifieurs. Un autre type de classe est cependant nécessaire : les fonctions d'échange. Elles produisent des objets très particuliers dont le but est d'assurer le bon déroulement des opérations. Notamment, la fonction de production de l'axiome produit l'amplifieur axiome qui représente la scène à sa précision la plus grossière.

L'algorithme de rendu récupère ces classes pour évaluer la forme visible en fonction d'une observation. L'observation fournit aux générateurs d'amplifieurs les paramètres nécessaires à la production des amplifieurs. C'est l'évaluation de ces amplifieurs qui va afficher la forme visible (cf. figure 5.3).

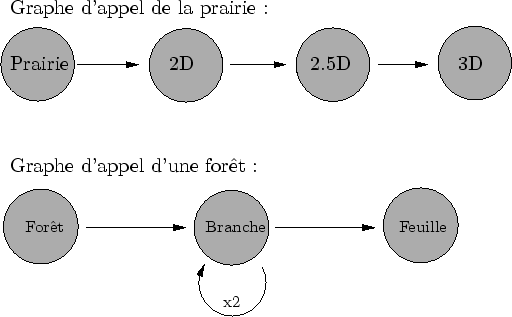
Lorsqu'un amplifieur ne suffit pas à la précision requise par une observation, il peut appeler d'autres amplifieurs qui vont continuer le travail qu'il n'a pas pu mener à terme. C'est naturellement au créateur de spécifier la manière dont un amplifieur peut générer des amplifieurs fils. La succession de ces appels définit un arbre d'évaluation (cf. figure 5.4).

**Figure 5.4:** Les générateurs d'amplifieurs s'appellent les unes les autres. De fait, Dynamic Graph permet une représentation très concise des structures répétitives. Par exemple, le générateur de branche, en s'appellant lui-même, permet de décrire un arbre très succintement en utilisant sa structure ``pseudo-fractale''.
$\begin{figure}\begin{center} \input{mod_arbre.pstex_t}\end{center}\end{figure}$

5.2.2 Arbre d'évaluation dynamique

Dans Dynamic Graph, chaque observation (i.e. affichage) nécessite une nouvelle évaluation de la forme. Une forme est évaluée par l'évaluation de tous les amplifieurs qui vont lui ajouter de la précision. Ces amplifieurs sont stockés dans un arbre d'évaluation. La génération de cet arbre s'arrête lorsque les critères de précision et de visibilité sont remplis.

5.2.2.1 Observation

Dans Dynamic Graph, on peut considérer la forme comme une fonction de l'observation. L'observation est notamment caractérisée par la position de la caméra et le temps. Plus généralement, l'observation est l'ensemble de tous les paramètres qui influent sur le rendu. Par exemple, on peut décider d'augmenter ou de diminuer le coefficient $Qualit\acute{e} \times Rapidit\acute{e}$ . La précision fait donc aussi partie de l'observation. Une forme peut être observée par plusieurs caméras. Dans ce cas, toutes les caméras font partie de l'observation.

Vous l'avez compris, l'observation est utilisée ici dans un sens très large. Du point de vue de la modélisation, l'observation représente indirectement toutes les inconnues, c'est-à-dire les paramètres des constructeurs des générateurs d'amplifieurs.

5.2.2.2 Construction de l'arbre d'évaluation

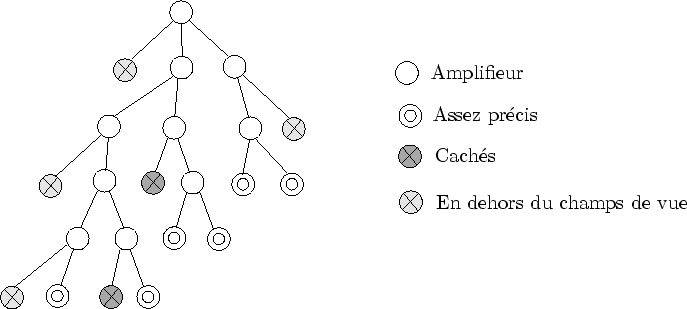
Lorsqu'un amplifieur ne suffit pas à la précision requise par une observation, nous avons vu qu'il peut appeler d'autres amplifieurs. La description proposée par Dynamic Graph impose que ces autres amplifieurs soient en fait engendrés par l'amplifieur en manque de précision. Ce choix est d'une importance capitale : il impose une description multi-échelle hiérarchique (ce choix sera discuté dans la section 8.1). Chaque noeud de l'arbre est un amplifieur et les fils d'un noeud sont les amplifieurs que celui-ci a créé. Cet arbre est appelé l'arbre d'évaluation (cf. figure 5.5).

**Figure 5.5:** Lorsque l'observateur se rapproche, l'arbre d'évaluation se développe. Il s'arrête lorsque l'objet est suffisamment précis ou non-visible.
$\begin{figure}\begin{center} \input{arbre_evaluation2.pstex_t}\end{center}\end{figure}$

5.2.2.3 Décomposition de l'évaluation

L'arbre d'évaluation représente en fait le résultat de l'évaluation. Plus précisément, il représente les étapes intermédiaires vers le résultat final : l'affichage sur l'écran.

Pour mieux comprendre cet arbre, on peut imaginer une personne faisant un immense calcul mathématique (une grosse équation) sur un tableau. Ce calcul étant très complexe, il préfère décomposer le calcul en plusieurs sous-problèmes. De cette façon, lorsqu'il sera bloqué sur un sous-problème, il pourra continuer sur un autre. Pour faire cela, il n'utilisera pas un tableau mais plusieurs petites ardoises. Lorsqu'il reprendra une ardoise, il pourra continuer le calcul qu'il y avait dessus car toutes les étapes y sont gardées en mémoire.

Dans l'arbre d'évaluation, chaque noeud est un amplifieur. Chaque noeud (i.e. amplifieur) de l'arbre d'évaluation est ``l'ardoise'' qui permet de retenir les calculs. Un nom plus précis de cet arbre serait donc : arbre de résultats partiels de l'évaluation. Pour simplifier, et par ``abus de langage'', nous employons le terme : arbre d'évaluation.

5.2.2.4 Critère d'arrêt

On peut, en connaissance d'une observation, calculer la précision d'un amplifieur. La précision joue un rôle essentiel dans les critères d'arrêt de l'évaluation de la forme. De plus, elle permet le calcul de la maturité. Cette dernière est un simple coefficient facilitant la réalisation de transitions continues entre niveaux de détail (c'est-à-dire entre amplifieur père et fils).

La forme contenue par un amplifieur peut ne pas être visible pour deux raisons :

il est hors-champ ;
il est caché par un autre objet.

D'une part, un simple calcul d'intersection entre la boîte englobante de l'amplifieur et la pyramide de vue est réalisé. D'autre part, un algorithme de visibilité est mis en oeuvre pour détecter les faces occultées afin ne pas afficher la géométrie cachée par d'autres géométries.

La construction s'arrête quand tous les amplifieurs sont soit assez précis, soit non visibles (cf. figure 5.6).

**Figure 5.6:** En fonction de l'observation, l'arbre d'évaluation va se générer jusqu'à sa complexion, c'est-à-dire quand toutes les conditions d'arrêt des feuilles sont positives. Comme les conditions d'arrêt dépendent de l'observation, l'arbre d'évaluation est différent à chaque affichage.
$\begin{figure}\begin{center} \input{critere_arret.pstex_t}\end{center}\end{figure}$

5.2.3 Une évaluation assistée

L'évaluation du modèle dans le but de son affichage est un procédé complexe assuré par Dynamic Graph. Avant de détailler dans le chapitre suivant les subtilités de cette évaluation, nous donnons ici un premier aperçu rapide.

Un organiseur, au moyen de visiteur (voir plus bas), contrôle l'ordre de l'évaluation de chaque amplifieur. Ce contrôle est nécessaire pour de nombreuses raisons, notamment à cause des contraintes émanant de l'algorithme de visibilité. Ce contrôle nécessite un échange complexe entre l'organiseur (via les visiteurs) et les amplifieurs.

5.2.3.1 Visiteur

Un visiteur est une fonction (un objet) qui parcours l'arbre d'évaluation et applique un traitement sur tous les noeuds (les amplifieurs). Chaque amplifieur est spécialisé grâce au polymorphisme et au mécanisme des fonctions virtuelles [Cha98]. Le traitement appliqué aux noeuds est donc différent pour chaque couple (visiteur,amplifieur).

Un visiteur sait comment stimuler un amplifieur : de leur échange naît l'information désirée. Voici les visiteurs couramment utilisés dans Dynamic Graph :

générateur:: ce visiteur construit l'arbre ;
destructeur:: ce visiteur détruit un arbre d'évaluation ;
redessinateur:: il redessine les informations contenu dans un arbre déjà généré ;
visualiseur:: il affiche l'arbre de façon formelle (noeud et arête), ce qui est utile lors du debogage du modèle.

Le générateur est le visiteur le plus important : c'est lui qui, à mesure qu'il parcourt l'arbre d'évaluation, construit ce dernier. Cela peut paraître paradoxal de parcourir un arbre en même temps qu'on le construit. Pour que le générateur puisse visiter un arbre comme s'il était déjà construit, il génère lui-même les fils des amplifieurs qu'il veut visiter plus profondément. Ce faisant, le générateur se maintient dans l'illusion de l'existence d'un arbre infini. Cet algorithme est inspiré des méthodes de la théorie des jeux telle que le branch and bound [BCL⁺99].

5.2.3.2 L'organiseur

**Figure 5.7:** On reprend ici la figure 5.2 en rajoutant l'organiseur et ses visiteurs. L'organiseur s'occupe du bon ordonnancement des tâches nécessaires aux contraintes émanant de certaines fonctionnalités (tel que l'algorithme de détection d'occultation).
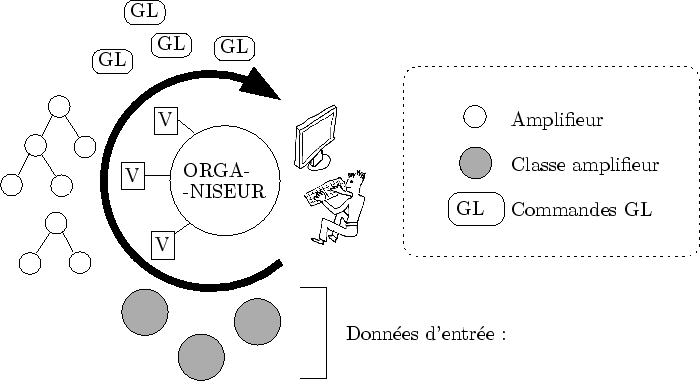$\begin{figure}\begin{center} \input{organiseur2.pstex_t}\end{center}\end{figure}$

L'un des rôles fondamental de l'algorithme de rendu est de bien distribuer le temps de calcul et d'activer tel ou tel amplifieur selon des critères de performances particuliers (que nous verrons en détails plus tard). L'algorithme de rendu est pour cette raison appelé l'organiseur : il organise l'activité pour optimiser les performances.

On peut ici reprendre les notions qui ont été nécessaires à la définition de la modélisation procédurale et en particulier, discuter du découpage entre ``programme'' et ``donnée'' (cf. sous-section 3.1.1). L'organiseur, avec ces visiteurs, est la partie du programme qui se trouve à la frontière des données d'entrée. Les générateurs d'amplifieurs, les amplifieurs et enfin les commandes OpenGL produites sont les données utilisateur à leur différentes représentations au fil de l'évaluation (cf. figure 5.7).

5.2.3.3 Évaluation par morceau

**Figure 5.8:** Dans Dynamic Graph, la construction de l'arbre d'évaluation est parfaitement contrôlée par l'organiseur. Contrairement à de simples fonctions récursives, Dynamic Graph permet de rendre la main à l'organiseur après la fin de l'évaluation de chaque amplifieur. De cette façon, l'organiseur a tous les pouvoirs pour diriger les opérations dans un ordre adéquat.
$\begin{figure}\begin{center} \input{recursif.pstex_t}\end{center}\end{figure}$

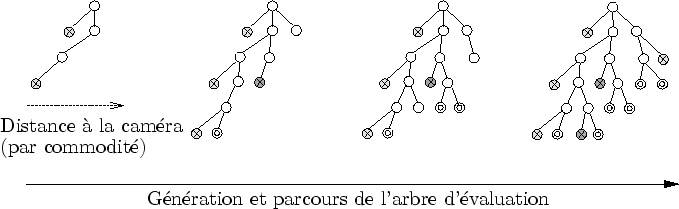
Comme les amplifieurs génèrent d'autres amplifieurs, on pourrait croire qu'une fois l'évaluation commencée, il est impossible de l'arrêter. Ce comportement est celui des fonctions récursives : les appels s'enchaînent sans jamais rendre la main jusqu'à ce que tous les critères d'arrêt soient satisfaits (cf. figure 5.8). Dynamic Graph propose un comportement similaire à ces fonctions récursives mais permet un bien meilleur contrôle de leur exécution.

Ce contrôle est essentiel pour diverses raisons. Notamment, l'ordre d'affichage des amplifieurs est important : l'algorithme de visibilité qui sera expliqué dans la section 6.3 nécessite un rendu de l'avant vers l'arrière. On pourrait construire tout l'arbre d'évaluation d'abord pour le trier et l'afficher ensuite. Malheureusement, ce même algorithme nécessite d'afficher les amplifieurs le plus tôt durant la construction : le premier amplifieur est rendu alors que la construction vient à peine de commencer.

Pour résoudre ce problème, l'arbre est construit approximativement de l'avant vers l'arrière (d'autres contraintes peuvent peser sur la construction). Lorsqu'un amplifieur est prêt à être affiché, l'organiseur le place dans une liste d'attente qui rétablit un ordre plus strict. Pour réaliser cela, un amplifieur, lorsqu'il génère des amplifieurs fils, construit ces derniers sans les évaluer. L'organiseur choisira plus tard s'il décide de les évaluer ou s'il est temps de lancer l'affichage de certains amplifieurs pour cela.

**Figure 5.9:** Un parcours trié en profondeur d'abord assure un rendu de l'avant vers l'arrière. Un noeud envoie ses commandes OpenGL dès que possible. Les feuilles visibles représentées par deux cercles imbriqués sont les amplifieurs les plus susceptibles de s'afficher. Sur ce schéma, par commodité de représentation, les amplifieurs à droite de l'arbre sont les plus distants de la caméra.
$\begin{figure}\begin{center} \input{graph_front2back.pstex_t}\end{center}\end{figure}$

5.2.3.4 Échange entre le modèle et le programme

L'organiseur doit être capable de communiquer avec les amplifieurs directement ou via un visiteur. Les fonctions d'échange s'occupent d'une partie de ce travail : elles fournissent notamment l'amplifieur axiome et assurent aussi certaines initialisations sans lesquelles le modèle ne peut pas être évalué. De plus, Dynamic Graph sait comment communiquer avec chaque générateur d'amplifieurs car ceux-ci héritent d'une classe virtuelle connue par l'organiseur.

Voici les fonctions que l'organiseur est susceptible d'appeler sur chaque amplifieur:

initialisation ;
fonctions diverses de navigation au sein d'un arbre (indiquer le fils, le père...) ;
génération des amplifieurs fils ;
affichage de la forme ;
calcul de la visibilité ;
calcul de la précision.

Dans certains cas, ces fonctions sont virtuelles pures, ce qui signifie que le créateur doit obligatoirement donner le code de cette fonction. Dans d'autres cas, ces fonctions sont virtuelles ``tout court'', ce qui signifie qu'un comportement par défaut est disponible. Pour des raisons diverses (performances, qualité, contrôle), le créateur peut choisir de personnaliser ces dernières pour un amplifieur particulier.

5.2.4 Animation

Dynamic Graph propose une évaluation de la forme visible à la volée. Afin de permettre l'optimisation par cohérence temporelle, des mémoires à plus ou moins long terme sont proposées au créateur. Un exemple simple et concret motive ce besoin.

5.2.4.1 Mémoire de l'information

À chaque pas de temps, un nouvel arbre d'évaluation est entièrement régénéré (i.e. la scène est entièrement reconstruite). En effet, la structure très dynamique de Dynamic Graph impose une évaluation à la volée. Utilisée naïvement, cette régénération supprime toute possibilité d'optimiser le programme par cohérence temporelle. Afin de ne pas passer son temps à recalculer la même fonction mille fois, Dynamic Graph permet une certaine mémoire des opérations effectuées aux pas de temps précédents.

Cette mémoire est principalement implémentée via un tampon d'arbres qui stocke les derniers arbres d'évaluation. Chaque arbre d'évaluation a accès aux arbres plus anciens et peut donc retrouver des résultats effectués récemment. Plus généralement, Dynamic Graph permet d'utiliser toute une panoplie de mémoires à plus ou moins long terme et propose différentes fréquences de calculs selon le type de fonction.

Voyons maintenant au travers d'un exemple simple une utilisation possible de la mémoire et de la cohérence temporelle.

5.2.4.2 Exemple : la brise légère

L'animation est calculée durant la construction d'un objet. Les fonctions d'animation modifient certaines données présentes dans les amplifieurs. Elle incrémente une position : $x=x+v.\delta t$ . Dynamic Graph propose des fonctionnalités avancées dans la gestion de la persistance des données. C'est un point essentiel du fonctionnement de Dynamic Graph, mais il est difficile à motiver de façon générale. Je vais donc l'introduire par un exemple.

On peut imaginer implémenter un mouvement par défaut de l'herbe, comme une brise légère^5.2. Cette fonction d'animation est réalisée par la donnée d'une position du brin d'herbe au repos : la brise légère induit de légères oscillations autour de cette position. Compte tenu de la génération à la volée, cette méthode pose un problème a priori anodin : où stocker cette position au repos ?

5.2.4.3 Durée de vie d'une information

Voici deux façons extrêmes et inappropriées d'accéder à cette information :

permanent:: mémoriser les positions au repos de tous les brins d'herbe induirait une description partielle au niveau le plus fin à éviter absolument ;
éphémère:: une fonction pseudo-aléatoire peut générer à la volée et à chaque pas de temps une position au repos pour chaque brin d'herbe. Ceci implique, pour tous les brins d'herbe, un calcul reproduit à l'identique à chaque pas de temps. De plus, l'information de cette position au repos sera stocké dans chaque amplifieur à chaque pas de temps, résultant en un gaspillage de place mémoire.

Dans le cas de description au niveau le plus fin, le problème de la durée de vie ne se pose pas : toute l'information existe à tous les pas de temps. En revanche, dans le cas d'une génération à la volée, la gestion de la persistance mémoire est beaucoup plus délicate. Dans l'exemple cité plus haut, il serait souhaitable, dans l'idéal, de n'allouer la position au repos d'un brin d'herbe qu'une fois par apparition sur l'écran : si, d'une image à l'autre, le même brin est visible, la même information peut être utilisée. Dynamic Graph permet ce genre de mécanisme et propose une gamme de mémoires dont la durée de vie varie de permanente à éphémère. Ces fonctionnalités sont une première forme simpliste d'optimisation par cohérence temporelle et sont le fondement de toute utilisation plus complexe de ce dispositif.

5.3 Bilan intermédiaire

5.3.0.1 Dynamic Graph

Les présentations sont faites. Dynamic Graph propose une nouvelle représentation d'une forme consistant en une description du plus grossier au plus fin. Le langage descriptif de Dynamic Graph est le C++ dont les caractéristiques orientées-objet sont utilisées pour permettre la communication entre l'algorithme de rendu et l'objet lui-même.

Compte tenu de cette représentation originale, la modélisation et le rendu sont très spécifique. En conséquence, aucun outil existant nous a semblé propice à prendre en charge une part des difficultés. C'est pourquoi Dynamic Graph est présent quasiment tout au long du processus de création^5.3.

5.3.0.2 La suite

Dans le chapitre 6, la phase d'évaluation sera détaillée. Une attention particulière sera portée sur la façon dont sont traités les deux critères d'arrêt : la précision et la visibilité.

Le chapitre 7 aborde Dynamic Graph du point de vue de l'utilisateur. J'y discute des outils proposés pour faciliter le développement de modèles et des résultats obtenus.

Notes

... exemple ^5.1: Afin d'éviter toute confusion, je tiens à signaler que la prairie n'a pas été implémentée avec Dynamic Graph. Néanmoins, l'adaptation ne poserait aucun problème.
... légère ^5.2: La brise légère anime donc tous les brins d'herbe, mais elle laisse aux autres primitives de vent la possibilité d'influencer. Du point de vue de l'amplifieur, on peut parler d'animation interne (la brise légère) et d'animation externe (les autres primitives de vent).
... création ^5.3: Sauf au stade final : l'utilisation des cartes graphiques, quelque soit l'application, est incontournable lorsque le temps-réel est visé.

Next: 6. Dynamic Graph : Up: main Previous: 4. Étude de cas

Frank Perbet
2004/04/25