Modélisation multi-échelle procédurale de scènes animées
Frank Perbet - 2004/04/25
next up previous contents
Next: 8. Conclusion Up: main Previous: 6. Dynamic Graph :

Sous-sections


7. Dynamic Graph : vue du créateur

Ce chapitre décrit Dynamic Graph du point de vue du créateur. C'est donc la partie modélisation qui est détaillée ici. La structure de ce chapitre est la suivante :

Environnement de modélisation:
la section 7.1 décrit l'environnement graphique de Dynamic Graph;
Création d'un amplifieur:
la section 7.2 décrit la tâche principale du créateur durant la modélisation : la création d'un amplifieur ;
Arbres animés
: la section 7.3 termine ce chapitre par la description du modèle le plus sophistiqué réalisé avec Dynamic Graph: des arbres agités par le vent.


7.1 Environnement de modélisation

Dans cette section sont détaillées les différents fonctionnalités que Dynamic Graph propose pour simplifier la modélisation.

7.1.1 Sous un autre angle

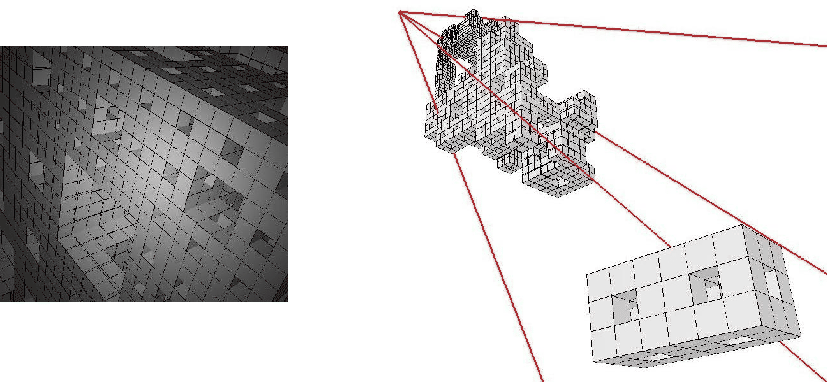
Les formes que Dynamic Graph génère s'adaptent à l'observation. Dans le meilleur des cas, on ne distingue pas cette adaptation lorsque l'on prend le point de vue de l'observateur : elle est invisible, camouflée. De plus, chaque mouvement de l'observateur provoque une transformation du modèle. il est parfois ``congeler'' le modèle pour pouvoir l'observer sous tous les angles. De cette façon, il est plus facile de déboguer et de trouver d'éventuels défaut.

Afin de permettre cela, Dynamic Graph propose, en plus de l'observation principale, une seconde observation, c'est-à-dire une observation pour laquelle la forme affichée reste adaptée à l'observation principale (cf. figure 7.1).

Figure 7.1: Une seconde observation permet un regard critique sur le modèle.
\begin{figure}\begin{center} \input{sec_obs.pstex_t}\end{center}\end{figure}

7.1.2 Sélection multi-échelle

La sélection est une opération de base dans toute modélisation. Dans Dynamic Graph, une sélection est un ensemble d'amplifieurs. La persistance de l'information est assurée par l'arbre permanent : les amplifieurs sélectionnés sont inscrits dans ce dernier.

Trois opérations de sélection classiques sont possibles :

Deux autres opérations plus originales sont propres à Dynamic Graph :

hiérarchique:
il est impossible de sélectionner graphiquement un amplifieur $\mathcal{A}$ qui n'affiche pas de géométrie. En revanche, il est possible de sélectionner un des amplifieurs contenu dans le sous-arbre de l'arbre d'évaluation (cf. section 6.1) dont $\mathcal{A}$ est la racine. Ensuite, il suffit de remonter d'amplifieur père en amplifieur père pour trouver $\mathcal{A}$. Dynamic Graph propose donc de transformer une sélection courante de façon hiérarchique : la nouvelle sélection est constituée par les père (resp. les fils) des amplifieurs de la sélection courante.
temporelle:
le tampon d'arbre (cf. section 6.1) garde une mémoire des $n$ derniers graphes d'évaluation. Pour accéder à un amplifieur ancêtre, il faut sélectionner l'amplifieur présent et remonter le temps (tant que le tampon d'arbre le permet). Dynamic Graph propose de transformer une sélection courante de façon temporelle : la nouvelle sélection est constituée par les ancêtres (resp. les successeurs) des amplifieur de la sélection courante.

7.1.3 Le DebugPanel

Dynamic Graph propose une boîte de dialogue composée de plusieurs champs de curseurs et de boutons : le debugPanel (cf. figure 7.2). C'est un outil d'aide à la modélisation.

Figure 7.2: Le debugPanel offre la possibilité de déclarer et de modifier dynamiquement une infinité autant de valeur que le souhaite le créateur. C'est en quelque sorte la version la plus primitive qui soit d'une interface graphique procédurale. Cet outil est très utile pour contrôler les très nombreux degrés de liberté qu'offre la modélisation procédurale.
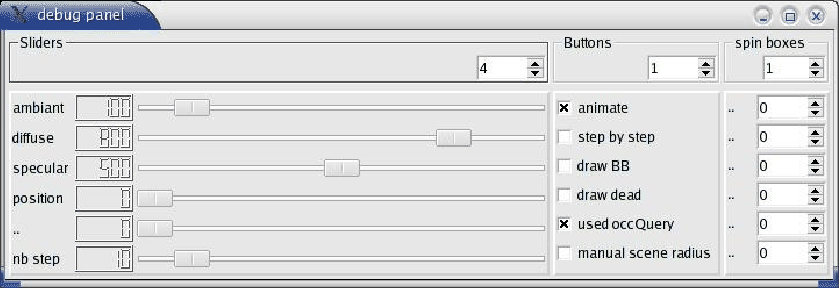\begin{figure}\begin{center} \input{debugPanel.pstex_t}\end{center}\end{figure}

Cet outil est un assistant très pratique à la modélisation avec Dynamic Graph. Avec une ligne de commande, on peut initialiser un curseur et lui donner un nom (par exemple : "taille cube" ou "couleur"). Avec une autre ligne de commande, il est possible d'appeler cette valeur. Durant l'exécution du programme, il devient alors possible de changer la valeur du curseur et d'en apprécier les conséquences.

7.1.4 Micro-interface graphique

Figure 7.3: Les micros-interfaces locales permettent d'interagir avec un amplifieur particulier.
\begin{figure}\begin{center} \input{dgselect.pstex_t}\end{center}\end{figure}

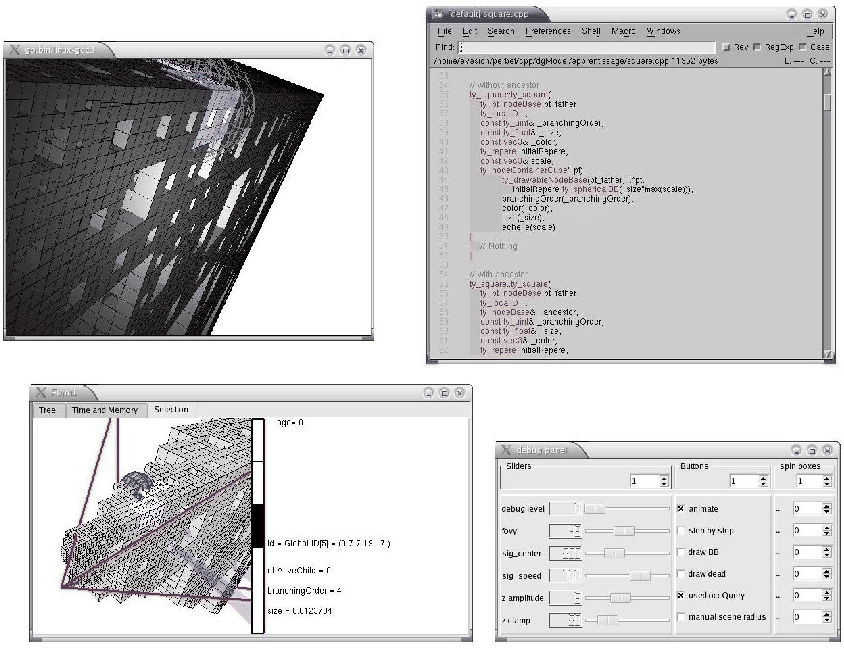
Dans les modeleurs classiques, il est possible de sélectionner une partie du maillage et de l'éditer. Cette opération est impossible en modélisation procédurale puisque aucune représentation géométrique n'est imposée. Néanmoins, afin de faciliter l'édition, le créateur peut, dans chaque amplifieur, coder une micro-interface graphique. S'il fait cela, il pourra, après avoir sélectionné un amplifieur, visualiser ses caractéristiques et interagir avec lui (cf. figure 7.3).

Concrètement, les interfaces graphiques sont uniquement basées sur OpenGL. Elles intègrent une gestion des évènements souris et clavier. Aucune bibilothèque d'interface n'a malheureusement été utilisée. Il serait intéressant d'associer à chaque amplifieur une interface dédié simple et facilement implémentable (des sortes de DebugPanel personnalisés).

L'utilisation la plus simple consiste à afficher, sous forme de texte, les caractéristiques de l'amplifieur sélectionné. Une utilisation plus complexe permettra une visualisation graphique éventuellement tridimensionnelle de certaines caractéristiques complexes de l'amplifieur. Enfin, il est possible, via les fonctions événements, d'interagir avec l'objet et, par exemple, de changer certaines valeurs à la volée.

7.1.5 Mesure de performance

Lors d'une modélisation procédurale assistée par Dynamic Graph, les coûts mémoires et les temps de calcul du rendu dépendent essentiellement des fonctions que le créateur a codé dans les amplifieurs. Il est donc très utile de pouvoir rapidement faire des mesures afin d'éviter de coder des amplifieurs trop gourmands en mémoire ou bien trop lents à calculer. Pour cela, Dynamic Graph fournit une visualisation de courbes de performances.

Plusieurs mesures de consommation de mémoire sont effectuées à chaque pas de temps :

Plusieurs mesures de temps de calcul sont réalisées :

7.1.6 Visualisation de l'arbre d'évaluation

De l'évaluation de la scène résulte l'arbre d'évaluation. La visualisation de ce dernier (cf. figure 7.4) s'avère dans certains cas fort utile. Par exemple, on peut sélectionner les amplifieurs directement dans cette fenêtre et naviguer plus facilement dans la hiérarchie de l'arbre.

De plus, en attribuant des couleurs particulières aux noeuds, il est possible de représenter certaines statistiques intéressantes sur les amplifieurs :

D'autres types de visualisation peuvent être définis. On peut imaginer, dans le cas particulier des prairies par exemple, afficher la densité de brins d'herbe de chaque amplifieur. Ici encore, Dynamic Graph ne propose pas de solution clef en main, mais une visualisation très souple et très paramétrable.

Figure 7.4: La visualisation de l'arbre d'évaluation donne un bon aperçu de la complexité de la scène.
\begin{figure}\begin{center} \input{dgtree.pstex_t}\end{center}\end{figure}

7.1.7 Temps réel, temps virtuel

Compte tenu du flux très dynamique d'informations durant l'exploration d'une scène animée multi-échelle, il est vital de maîtriser l'écoulement du temps. Pour cela, Dynamic Graph offre un paramétrage très souple du couple $(f_{virtuel},f_{reel})$ :

Dynamic Graph peut forcer la valeur de $f_{virtuel}$ sans tenir compte de $f_{reel}$. L'inverse est aussi possible grâce à une régulation très simple de la fonction de précision, via la valeur $S_{ideale}$ (cf. section 6.2). Il est possible d'asservir ces deux valeurs. Par exemple, un asservissement $f_{virtuel}=f_{reel}$ est caractéristique d'un affichage temps-réel.

Il est aussi possible de contrôler manuellement $f_{reel}$ : c'est le pas à pas. Il permet de faire avancer l'animation image par image et de détecter, par exemple, l'éventuelle apparition de bogue. Toujours dans la même optique, Dynamic Graph permet de décomposer $f_{reel}$ et de générer l'arbre d'évaluation progressivement. Chaque étape de l'organiseur est alors déclenchée manuellement.

Il est possible de passer d'un mode à l'autre durant l'exécution du programme.

Figure 7.5: Exemple typique de modélisation avec Dynamic Graph. En haut à gauche, la fenêtre affiche l'objet tel qu'il est vu par l'observateur principal. En bas à gauche, une seconde observation permet de contrôler la manière dont le modèle s'adapte au point de vue ; la sélection permet d'accéder aux micro-interfaces graphiques. En bas à droite, le debugPanel permet de changer dynamiquement certaines valeurs. En haut à droite, un éditeur de texte permet la modélisation des amplifieurs.
\begin{figure}\begin{center} \input{env.pstex_t}\end{center}\end{figure}


7.2 Création d'un amplifieur

Les amplifieurs sont la base du langage descriptif de Dynamic Graph. Nous allons voir ici les détails de la création d'un générateur d'amplifieurs dans le cas simple du cube de Sirpienski. Nous décrirons tout d'abord rapidement l'environnement de travail. Nous détaillerons ensuite les étapes nécessaires à la création d'un amplifieur. Enfin, nous nous attarderons sur quelques points sensibles auxquels le créateur doit prêter une attention particulière.

7.2.1 Cadre de travail

Compte tenu de l'aspect très particulier de la modélisation que propose Dynamic Graph, nous décrivons ici le cadre de travail d'un point de vue très général. Du point de vue du Dynamic Graph, un modèle (i.e. une forme tridimensionnelle) est une librairie dynamique (sous linux, un fichier dont l'extension et so). Les fonctionnalités décrites en 7.1 assistent le créateur dans sa tâche. Lors de la modification d'un modèle, Dynamic Graph recharge dynamiquement la librairie sans cesser son éxécution afin de rendre compte des modifications le plus vite possible.

7.2.1.1 Le projet

Très concrètement, comment se passe une session de modélisation? Tout d'abord, il faut créer le ``projet'' correspondant à un modèle. Ce projet va générer l'infrastructure nécessaire à la réalisation du modèle : un dossier, un fichier Makefile et le fichier principal. Ce fichier principal contient les fonctions d'échange (cf. sous-section 5.2.3).

Par exemple, c'est ici que la fonction de production de l'axiome est définie. D'autre fonctions d'échange permettent d'initialiser la librairie dynamique en éxécutant une fonction particulière lors du chargement. Il est aussi possible d'éxécuter une fonction avant chaque affichage. Parallèlement à ces fonctions d'initialisation existe des fonctions de terminaison.

7.2.1.2 L'interface

La figure 7.5 décrit une configuration classique de l'environnement. La modélisation se passe essentiellement dans l'éditeur de texte. Remarquons que l'éditeur de texte est parfaitement indépendant de Dynamic Graph. Dans la figure 7.5, l'éditeur utilisé est NEdit augmenté de quelques macro-fonctions dédié à Dynamic Graph.

7.2.1.3 Une classe C++

Un amplifieur est une transformation de la forme tridimensionnelle qui consiste à ajouter de la précision. Concrètement, il est représenté par une classe C++ héritant d'une classe virtuelle. Celle-ci impose au créateur de remplir certaines fonctions :

constructor:
construit une instance de classe (un amplifieur) ;
createChild:
construit les instance filles (amplifieur plus précis) ;
draw:
envoie les commandes OpenGL pour dessiner la forme ;
drawBoundingBox:
envoie les commandes OpenGL pour dessiner la boîte englobante.
Ces fonctions seront détaillées dans la sous section suivante 7.2.2.

7.2.1.4 Compilation à la volée

Lorsque le créateur veut afficher le modèle qu'il a écrit dans son éditeur préféré, il lance une compilation. Évidemment, il lui faudra sûrement corriger quelques erreurs. Lorsque la compilation réussit, une librairie dynamique est créée (ou modifiée si elle existe déjà).

Dynamic Graph peut charger à la volée des modèles (i.e. des librairies dynamiques). Par exemple, lors d'une modification de la librairie dynamique, Dynamic Graph détectera cette dernière et fera la mise à jour automatiquement. Ce comportement engendre quelques soucis techniques, mais il est néanmoins tout à fait naturel de la part d'un modeleur : lorsque l'on modifie un objet, on veut en voir les répercussions immédiatement.

La latence entre une modification et sa répercussion sur l'écran est égale au temps de compilation. Dans le cas du cube de Sirpienski, cette durée vaut environ $5$ secondes (sur une machine standard achetée en 2003).


7.2.2 Détail des fonctions

Voyons maintenant plus précisément le contenu de chaque fonction de l'amplifieur : le constructeur, la fonction d'affichage, les boîtes englobantes et la génération des fils. Nous terminerons par quelques résultats de modélisation de fractales.

7.2.2.1 Constructeur

Le rôle du constructeur est principalement d'initialiser les valeurs des variables membres. Voici à quoi ressemble l'entête du constructeur :


\begin{table}\begin{verbatim}square(int localID, float _size, repere localRepere)\end{verbatim} \end{table}

les paramètres caractérisant un amplifieur sont sa taille et son repère local (exprimé dans le repère de la caméra). L'identifieur local est aussi nécessaire : rappelons qu'il permet de distinguer un amplifieur parmi ses frères.

Le constructeur est appelé durant la création de l'amplifieur axiome et à chaque génération d'amplifieurs fils.

7.2.2.2 Fonction d'affichage

Figure 7.6: La fonction draw de l'exemple du cube de Sirpienski dépend de la maturité de l'amplifieur. Cet objet est le seul utilisé lors de l'affichage de la fractale.
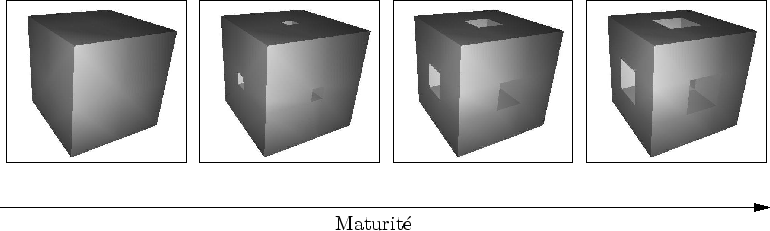\begin{figure}\begin{center} \input{csbase.pstex_t}\end{center}\end{figure}

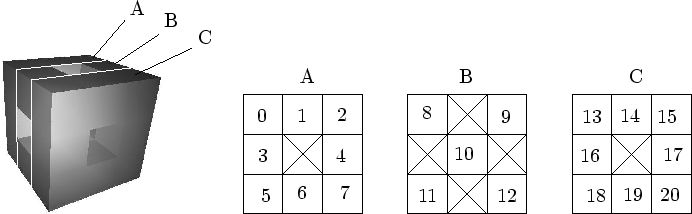
Dans le cas du cube de Sierpinski, la fonction draw dessine l'objet représenté sur la figure 7.6. Cet objet est défini procéduralement : il est généré et envoyé à la carte graphique à la volée.

La fonction d'affichage envoie les commandes OpenGL à la carte graphique. Elle n'a aucun paramètre et utilise généralement les données stockées dans l'amplifieur. Par exemple, dans le cas du cube de Sierpinski, la fonction est la suivante :


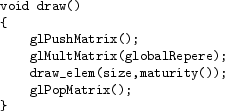
\begin{table}\begin{verbatim}void draw() { glPushMatrix(); glMultMatrix(globalRepere); draw_elem(size,maturity()); glPopMatrix(); }\end{verbatim} \end{table}

Les variables globalRepere et size sont des variables membres de l'amplifieur. La fonction maturity() renvoie la maturité de l'amplifieur.

Figure 7.7: Les sous cubes de l'élément de base sont numérotés. La fonction getRepere donne la translation entre le repère de l'élément (centré sur celui-ci) et les $20$ sous repères.
\begin{figure}\begin{center} \input{cube_tranche.pstex_t}\end{center}\end{figure}

Figure 7.8: Pour une qualité aussi haute, la fréquence d'affichage est d'environ $1Hz$. Remarquons tout de même que la taille des détails observés, pour un cube initial mesurant un mètre, sont de l'ordre du micromètre.
\begin{figure}\begin{center} \input{showcube.pstex_t}\end{center}\end{figure}

Figure 7.9: Différentes fréquences d'affichage : la qualité est inversement proportionnelle aux performances.
\begin{figure}\begin{center} \input{cubeDetail.pstex_t}\end{center}\end{figure}

Figure 7.10: Un zoom sur la pyramide de Sirpienski.
\begin{figure}\begin{center} \input{pyzoomr.pstex_t}\end{center}\end{figure}


7.2.2.3 Boites englobantes

Remarquons qu'il appartient au créateur de spécifier la boîte englobante de chaque amplifieur. Un calcul automatique des boîtes englobantes est tout simplement impossible puisque il faudrait parcourir une infinité d'amplifieur pour s'assurer que rien ne ``dépasse''. Remarquons à cette occasion un travail récent proposant un calcul automatique de boîtes englobantes hiérarchiques [LH03]. Cette approche est possible grâce au formalisme et aux restrictions propres au langage des IFS. Dans le cadre de Dynamic Graph, l'expressivité du C++ rend complètement impossible ce genre de calcul.

Demander au créateur de spécifier les boîtes englobantes des amplifieurs qu'il modélise peut sembler très contraignant. Mais cela est en partie justifié. Remarquons cependant que les boîtes englobantes ne doivent pas être très précises. Par exemple, des boîtes englobantes deux fois plus grosses que ce qu'elles devraient influencent peu les performances. Ceci est du à l'utilisation de boîte englobante hiérarchique : à la fin de la décomposition, les boîtes englobantes sont de toute façon très petites et ne déborderont pas beaucoup du champ de vue.

Le créateur doit fournir différents types d'information sur l'occupation de l'espace :

Encore une fois, il peut sembler contraignant de demander autant d'information au créateur. Mais dans le cas où celui-ci est paresseux, il peut ne fournir que la boîte englobante sphérique dont seront déduits les deux autres type d'information.

Dans le cas du cube de Sirpienski, seul la boîte englobante sphérique est spécifiée.

7.2.2.4 Génération des fils

Lorsque la précision est insuffisante, les amplifieurs fils sont générés. Voici à quoi ressemble le corps de la fonction childGeneration :


\begin{table}\begin{verbatim}void square::childGeneration() { for(int i=0;i<2... ...e,newRepere); childContainer.addChild(newChild); } }\end{verbatim} \end{table}

La fonction getRepere donne la transformation entre un repère et les $20$ repères des amplifieurs fils (cf. figure 7.7).

7.2.2.5 Résultat

Les figures 7.8, 7.9 et 7.10 montrent quelques captures d'écran. Même si ces modèles ne sont pas animés, les résultats sont plus impressionnants lorsque la caméra est en mouvement. Des vidéos sont disponibles sur le site http://www-evasion.imag.fr/$\sim$Frank.Perbet/these. Ces modèles ont été réalisé par Sandrine Bard et Benjamin Rouveyrol, deux stagiaires qui débutaient en modélisation 3D, en une semaine. Ils ont aussi réalisé un modèle d'arbre qui sera décrit en 7.3.

7.2.3 Quelques points sensibles

L'étude de ce cas simple cache quelques subtilités dont il est important d'être conscient. Nous parlerons tout d'abord ici de la zone d'influence d'un amplifieur. Nous expliquerons ensuite pourquoi le choix des conteneurs des amplifieurs fils est laissé au créateur. Enfin, nous parlerons des différentes mémoires que Dynamic Graph propose et de leur utilisation dans le cadre de l'optimisation par cohérence temporelle.

7.2.3.1 Zone d'influence d'un amplifieur

Figure 7.11: Lors d'une observation, les amplifieurs enrichissent différentes zones et sous-zones de la forme. Dans Dynamic Graph, rien n'assure le bon positionnement des zones les unes par rapport aux autres. En conséquence, certains comportements maladifs peuvent survenir.
\begin{figure}\begin{center} \input{zone.pstex_t}\end{center}\end{figure}

Un amplifieur est une transformation de la forme tridimensionnelle qui consiste à l'amplifier (i.e. à ajouter de la précision). Pour chaque amplifieur, on peut déterminer la partie d'un objet qu'il amplifie. La fonction draw dessine précisément cette partie amplifiée. De même, la boîte englobante entoure cette partie (ainsi que toute la géométrie pouvant être amplifiée à partir de celle-ci).

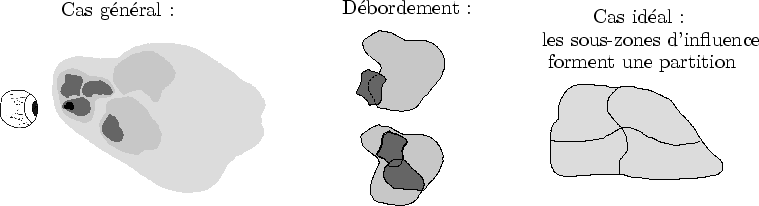
On peut imaginer que la forme est marquée au feutre sur l'objet de différentes zones d'influence correspondant chacune à un amplifieur. Chaque zone est à son tour marquée par les zones des amplifieurs fils, et ainsi de suite. La figure 7.11 schématise ces zones d'influence en deux dimensions.

Remarquons que dans Dynamic Graph, ces zones d'influences ne sont représentées par aucune structure. Elles n'existent que par le simple fait que les amplifieurs modifient une certaine partie des informations représentant la forme. En fait, malgré le fait que la métaphore visuelle soit plus intuitive, il est plus juste de définir une zone d'influence comme l'ensemble des données en mémoire modifiées par un amplifieur.

Lorsque plusieurs amplifieurs modifient les mêmes parties d'un objet, plusieurs zones d'influence peuvent s'intersecter : on parle alors de zone sous influences multiples. Ces dernières posent de sérieuses difficultés :

Dans le cas de structures très hiérarchiques tel que le sont tous les modèles présentés dans ce manuscrit, les zones d'influences sont parfaitement disjointes, évitant du coup cette difficulté. Dans le cas de structures continues, il est évident que le problème se pose. On peut par exemple imaginer que la figure 7.11 représente un terrain et que les amplifieurs ajoutent des montagnes.

Une solution consisterait à imposer un ordre d'évaluation, ou à s'assurer de la commutativité des amplifieurs. Mais comment savoir s'il faut afficher, à un instant donné, les parties de l'objet appartenant à la zone d'influence d'un amplifieur ? En effet, peut-être que celle-ci sera modifiée ultérieurement par un autre amplifieur, auquel cas il faut retarder l'affichage.

Toute cette problématique semble mettre en avant un lien étroit entre zone d'influence et boîte englobante (i.e. zone ``influençant''). En effet, si une zone d'influence avait connaissance des boîtes englobantes, elle pourrait décider de ne s'afficher que lorsqu'aucune boîte englobante ne l'intersecte (et donc qu'aucun amplifieur ne l'influence). Ceci implique une représentation de la géométrie intelligente et capable de déterminer les zones qu'elle peut afficher sans risque.

Dynamic Graph n'apporte pas de solution à ces problèmes. Plus généralement, il est clair que cet outil est mieux adapté aux structures hiérarchiques. Ceci sera discuté plus en profondeur en 8.1 : nous y verrons comment il est possible de contourner ces limitations.

7.2.3.2 Conteneur des fils

Rappelons que le conteneur des fils est la structure de donnée qui recense tous les fils d'un amplifieur père. Un amplifieur, lorsque la forme nécessite plus de précision, engendre un certain nombre de sous-amplifieurs pouvant être de type différent. Les amplifieurs enfants sont référencés dans un conteneur de l'amplifieur parent. Ce conteneur est utilisé intensivement par l'organiseur lors des parcours de graphe.

Or, de façon générale, aucun conteneur n'est efficace pour stocker n'importe quel type de donnée : parfois, un tas sera efficace, d'autres fois une table de hachage, parfois un simple tableau... Dans Dynamic Graph, le problème vient du fait que les amplifieurs peuvent représenter de très nombreuses formes de nature très différente. Un choix générique de conteneur compromettrait donc les performances de l'organiseur.

De plus, une fonction de tri est appliquée aux conteneurs à chaque pas de temps afin de réaliser un rendu d'avant en arrière. Ce tri, s'il n'est pas fait avec précaution, peut coûter cher et ralentir notablement les performances. La répartition spatiales des sous-amplifieurs suit souvent des lois connues (cf. figure 4.5 du chapitre 4) qui peuvent être mises à profit pour accélérer le tri.

Ainsi, le créateur doit lui même choisir quel conteneur utiliser parmi ceux proposés par défaut. Éventuellement, il peut en recoder un pour un cas très particulier. C'est ce qui a été fait pour le cube de Sirpienski : la connaissance très particulière de la structure du cube (cf. figure 7.7) a permis de réaliser un conteneur adapté très efficace.

7.2.3.3 Mémoire et cohérence temporelle

Dynamic Graph propose un mécanisme d'évaluation à la volée. S'il était utilisé naïvement, toute la partie visible serait régénérée à chaque pas de temps. Afin de pouvoir réutiliser certaines informations d'un pas de temps sur l'autre, Dynamic Graph propose des mémoires à différente durée de vie (cf. figure 7.12).

Figure 7.12: Plusieurs types de mémoire sont visibles depuis un amplifieur. Chacune d'elles a une durée de vie particulière. La mémoire permanente est allouée pour toute la durée de l'exécution de Dynamic Graph. La mémoire mortelle est allouée à la naissance d'un amplifieur et désallouée à sa mort. La mémoire éphémère est celle stockée dans le tampon d'arbres : elle dure 2 ou 3 pas de temps.
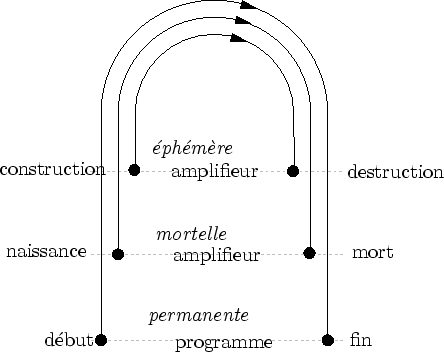\begin{figure}\begin{center} \input{mem.pstex_t}\end{center}\end{figure}

Afin de fixer les idées, voici, pour chaque type de mémoire, un exemple d'utilisation :

mémoire permanente:
supposons que l'on veuille dessiner l'un des éléments du cube de Sirpienski en rouge, et non en gris. Grâce à l'arbre permanent (cf. sous-section 6.1.3), ceci est possible en ajoutant dans la mémoire permanente associée à un amplifieur une fonction imposant cette caractéristique ;
mémoire mortelle:
supposons que la géométrie dessinée par un amplifieur soit parfaitement statique. On peut alors la décrire grâce à un vertex array. Celui-ci sera alloué lors de la naissance de l'amplifieur et désalloué lors de sa mort (cf. sous-section 6.1.2) ;
mémoire éphémère:
lors d'une animation, le créateur peut utiliser une fonction faisant intervenir des valeurs à des temps passé. C'est le cas, par exemple, d'un calcul d'accélération :

\begin{displaymath} a(t)=\frac{x(t)-2.x(t-\delta t)+x(t-2.\delta t)}{\delta t^2} \end{displaymath}

La position étant stockée dans chaque amplifieur, le tampon d'arbres (cf. sous-section 6.1.2) permet ce calcul par la reformulation :

\begin{displaymath} a_{courant}=\frac{x-2.x_{anc\grave{e}tre}+x_{anc\grave{e}tre^2}}{\delta t^2} \end{displaymath}

La bonne utilisation de ces mémoires est essentielle à de bonnes performances lors de l'évaluation et de l'affichage. Ces mémoires sont le support principal de l'utilisation de la cohérence temporelle.


7.3 Arbres animés

Dans cette section, nous présentons l'exemple de modèle le plus abouti réalisé avec Dynamic Graph : un modèle d'arbre animé. Nous présenterons ce modèle non pas comme un travail de recherche, mais comme une validation de Dynamic Graph comme outil d'aide à la modélisation multi-échelle. Nous décrirons donc rapidement un super-cylindre qui est quasiment la seule primitive graphique utilisée dans le modèle. Nous détaillerons ensuite la structure du modèle et les différents amplifieurs qui le constituent. Enfin, nous décrirons brièvement l'animation et montrerons les résultats.

7.3.1 Présentation

Nous dévoilons ici l'idée générale sur laquelle est bâti ce modèle. Nous expliquons ensuite le contexte de cette réalisation afin de mieux valider Dynamic Graph.

7.3.1.1 Idée générale

Le modèle le plus abouti réalisé avec Dynamic Graph est un arbre. L'arbre réalisé est extrêmement paramétrable. Cela ne signifie pas que toutes les espèces peuvent être modélisées mais nous pensons néanmoins que la structure mise en place peut être adaptée facilement à de nombreux cas particuliers.

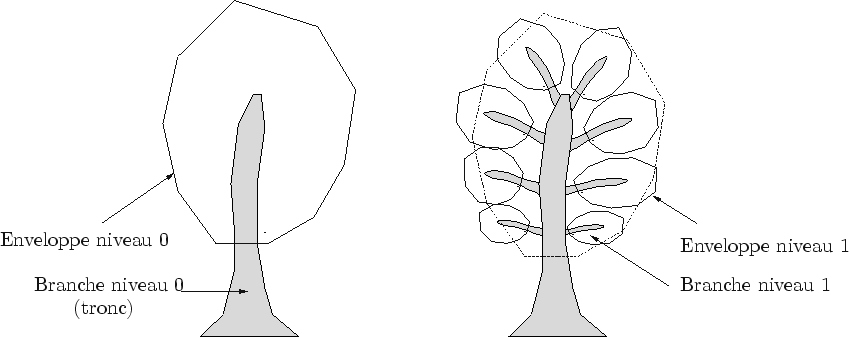
Les niveaux de détail reposent sur la structure de l'arbre ``biologique'' : le tronc, les branches, les sous-branches (cf. figure 7.13). Cette structure a le mérite d'être un excellent codage de la répétitivité : deux générateurs d'amplifieurs sont suffisants : les branches et les feuilles. Les niveaux de détail grossiers sont supportés par les enveloppes des branches : à la place des feuilles contenues par une enveloppe, seule cette dernière est affichée avec une texture ``feuillue''. L'animation est réalisée de manière procédurale de façon très similaire aux prairies. Des primitives de vent (une brise légère et des bourrasques) dictent le mouvement de l'arbre.

Figure 7.13: La structure générale, similaire à [BPF+03], est la suivante : de loin, un arbre est représenté par un tronc et une enveloppe. Lorsque l'observateur se rapproche, la grande enveloppe disparaît pour laisser la place aux branches et à leurs enveloppes.
\begin{figure}\begin{center} \input{arbre_str0.pstex_t}\end{center}\end{figure}

Notons qu'un modèle similaire a été conçu par Lars Mündermann lors de sa thèse sous la direction de Przemyslaw Prusinkiewicz, suite à leurs travaux sur «l'information positionnelle» [PMKL01]. L'implémentation avait été réalisée avec L-Studio[PHM99]. Il est extrêmement intéressant que ce logiciel, initialement conçu pour simuler la croissance de plante, ait pu être ``détourné'' vers la multi-échelle. En fait, le lien entre la croissance et la multi-échelle est très fort : on peut imaginer qu'un jeune arbre est une version grossière (mais plus petite) de l'arbre mature. Pour vous en convaincre, je vous renvoie à l'excellent livre «The art of genes» de Enrico Coen [Coe00].

7.3.1.2 Contexte

Ce travail est présenté non pas comme un travail de recherche, mais comme un produit de Dynamic Graph. Il est donc important de préciser le cadre dans lequel il a été réalisé. Dynamic Graph, en proposant une modélisation très fondamentale (procédurale), n'est pas un outil facile à utiliser et il n'est guère possible de le faire tester en quelques heures par quelques victimes choisies dans l'entourage. J'ai eu la chance d'encadrer deux stagiaires, Sandrine Bard et Benjamin Rouveyrol, qui, durant sept semaines, ont chacun utilisé Dynamic Graph dans le but de modéliser ces arbres agités par le vent. Par ailleurs, ce sont aussi les auteurs des exemples de fractales utilisés en 7.1.

Ces deux personnes ont réalisé une sorte de validation très informative. Afin de pouvoir mieux valider Dynamic Graph en tant qu'outil générique, voici en quelque sorte le ``protocole expérimental'' utilisé :

Vous savez tout, passons maintenant à la description du modèle. Les temps passés sur les différents stades du développement seront chiffrées en semaines cumulées, comme si une seule personne avait travaillé plus longtemps. Avec cette unité, la réalisation des arbres a durée 10 semaines au total (2 fois 5 semaines).

Figure 7.14: Deux fonctions définissent un super-cylindre. La forme s'affiche avec une mise à l'échelle à la volée et un échantillonnage en $z$ de l'axe et en $(z,\theta)$ de l'enveloppe.
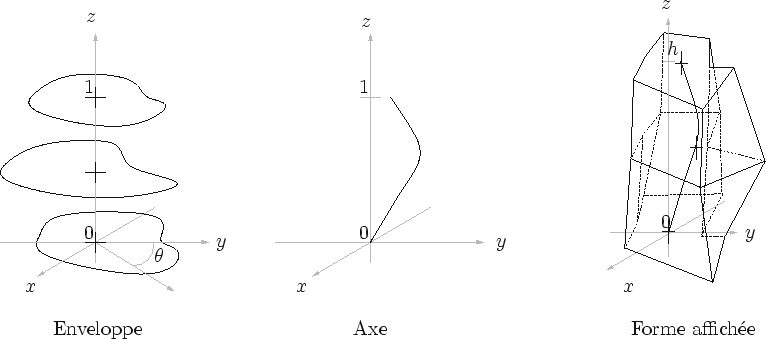\begin{figure}\begin{center} \input{supercyl.pstex_t}\end{center}\end{figure}

7.3.2 Super-cylindre

A l'exception des feuilles, les arbres sont affichés via un seul type de primitives géométriques : des cylindres généralisés normalisés, adaptatifs et procéduraux (générés à la volée). Par commodité, nous les appellerons super-cylindre. Leur implémentation a pris 6 semaines, soit plus de la moitié du temps.

7.3.2.1 Un axe et une enveloppe

Un super-cylindre est principalement caractérisé par deux fonctions (cf. figure 7.14) :

axe:
$[0,1] \stackrel{axe}{\longmapsto} [0,1] \times [0,1]$ tq $axe(0)=(0,0)$ ; cette fonction décrit l'axe du cylindre.
enveloppe:
$[0,1] \times [0,2\pi] \stackrel{env}{\longmapsto} [0,1]$; cette fonction décrit l'enveloppe du cylindre.
La seule contrainte posée sur ces fonctions est d'être rapidement calculable (des splines font très bien l'affaire).

Lors d'un affichage, un super-cylindre est généralement mis à l'échelle. Stocker l'information sous une forme normalisée ne change rien conceptuellement. Cela offre néanmoins un moyen pratique pour créer une banque de fonctions facilement réutilisables .

7.3.2.2 Multi-échelle

Lors de l'affichage, un super-cylindre est échantillonné en triangles puis envoyé sur la carte graphique. Cet échantillonnage est adaptatif et permet de concentrer l'échantillonnage des triangles là où c'est le plus nécessaire (cf. figure 7.15).

Figure 7.15: L'échantillonnage dynamique de l'axe et de l'enveloppe d'un super-cylindre lui permet d'adapter continûment sa précision à l'observation. Cette structure est mise à jour par modification : à chaque pas de temps, un parcours de liste permet d'enlever ou de supprimer certains points. Un super-cylindre est stocké dans la mémoire mortelle.
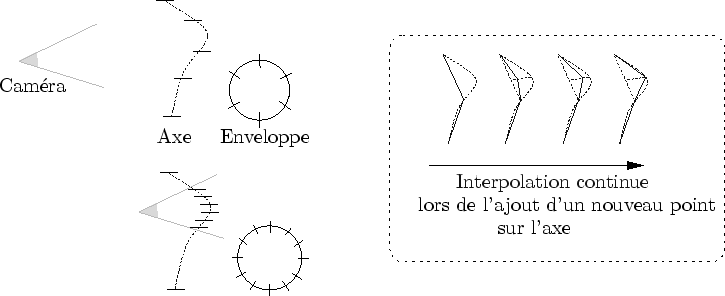\begin{figure}\begin{center} \input{supercylmr.pstex_t}\end{center}\end{figure}

Lors d'une mise à jour, la liste d'échantillon est parcourue :

Des interpolations continues sont réalisées lors de l'ajout ou la suppression d'un nouveau point.

7.3.2.3 Texture

Lors de l'affichage à la volée d'un super-cylindre, il est possible de lui associer une texture grâce à un plaquage cylindrique. Des textures répétitives en hauteur et en largeur sont utilisées pour éviter les discontinuités.

Un effort particulier a été réalisé pour contrôler le canal Alpha. Celui-ci est représenté par une texture indépendante grâce au multiTexturing [WND99]. Nous verrons dans la sous-section suivante comment la transparence que permet la fonction glAlphaTest est utilisée pour donner un aspect feuillu.

7.3.3 Structure du modèle

Cette partie décrit principalement le générateur d'amplifieurs principal : la branche. Les générateurs de forêt et de feuille seront aussi décrits, mais leur temps de développement a été négligeable. Le travail présenté dans cette sous-section, décrivant les mécanismes essentiels du modèle, a été réalisé en 3 semaines.

7.3.3.1 Enveloppe et tronc

Un amplifieur peut dessiner une enveloppe et un tronc. Le tronc est dessiné grâce à un super-cylindre texturé. Un amplifieur affiche le tronc quelque soit la précision, même s'il a engendré des amplifieurs fils.

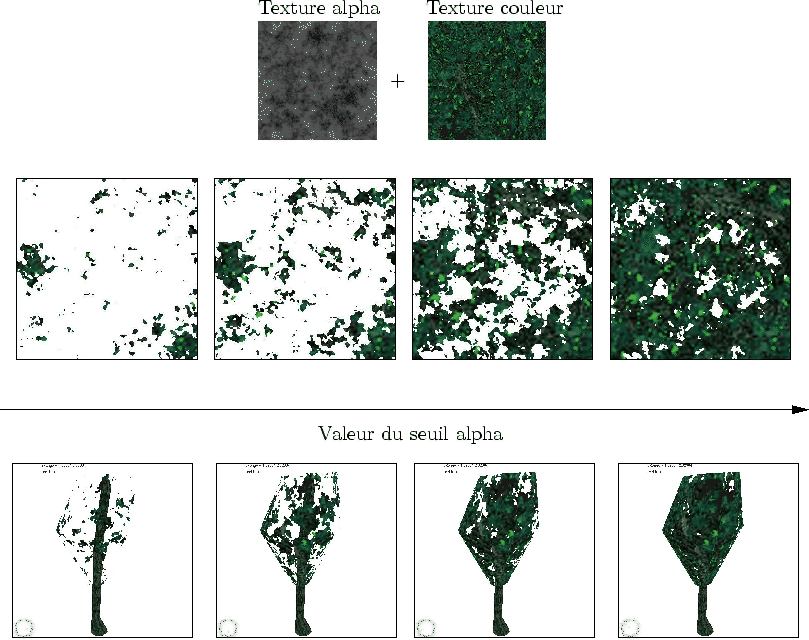
L'enveloppe est dessinée avec un super-cylindre plus large, texturée de façon semi-transparente. La texture de couleur est une texture de bruit évoquant l'apparence d'un feuillage. En jouant sur le seuil Alpha de la fonction glAlphaTest, on peut changer la densité de feuilles (cf. figure 7.16) Cette représentation est, à une certaine distance, suffisante pour rendre l'aspect chaotique du feuillage de l'arbre.

Figure 7.16: L'enveloppe est texturée par un image RGB et une image alpha. Le canal Alpha module la densité de feuille dans l'arbre.
\begin{figure}\begin{center} \input{texarbre.pstex_t}\end{center}\end{figure}

7.3.3.2 Ajout d'un niveau supérieur

Pour passer de l'arbre représenté par un seul amplifieur (tronc et enveloppe) au niveau de détail supérieur, les enveloppes des branches principales sont ajoutées progressivement (cf. figure 7.17).

Figure 7.17: Transition entre deux niveaux de détail : les sous-amplifieurs apparaissent tandis que l'amplifieur père disparaît. Reqmarquez qu'il aurait été intéressant de réaliser un fondu continue de la transparence au lieu de la transparence ``tout ou rien''. Mais la fonction glBlendFunc, nécessaire pour avoir une transparence continue, est délicat à utiliser car elle nécessite un rendu parfaitement trié des polygones. De plus, même si la transparence utilisée ici est ``tout ou rien'', elle apparaît et disparaît de façon spatiallement continue, ce qui est rend le procédé très acceptable d'un point de vue perceptuel.
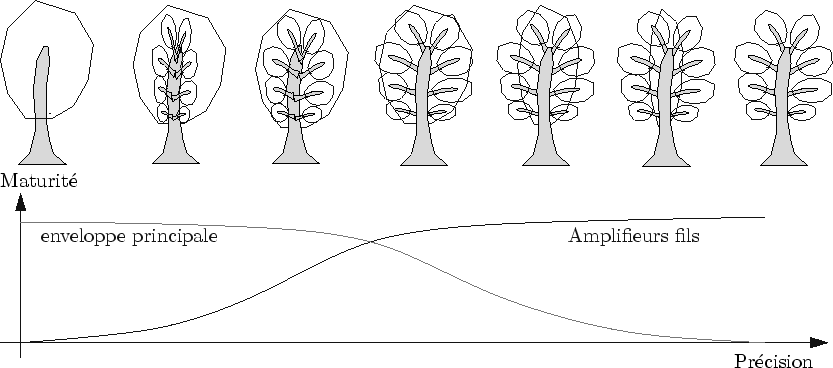\begin{figure}\begin{center} \input{arbre_str1.pstex_t}\end{center}\end{figure}

On peut décomposer la vie d'un amplifieur «branche» en différentes phases (cf. figure 7.18):

non-existence:
lorsque l'observateur est trop loin, l'amplifieur n'existe pas ;
première transition (apparition):
lorsque la précision augmente, l'amplifieur ``pousse'' verticalement (selon son repère local). Dans le cas du tronc, tout se passe comme si l'arbre sortait du sol. L'amplifieur est initialement constitué d'une enveloppe et d'une branche ;
premièr état stable :
dans une certaine plage de précision, l'arbre s'adapte à la précision grâce aux possibilités offerte par les super-cylindres ;
seconde transition (disparition de l'enveloppe):
lorsque la précision augmente encore, l'enveloppe se rassemble sur son axe (homothétie axiale) et disparaît. Le tronc reste.
second état stable:
ensuite, seul le tronc est dessiné. Il continue à adapter sa précision grâce aux super-cylindres.

Figure 7.18: Différentes étapes d'un amplifieur en fonction de la précision. Deux fonctions de maturité assurent le passage d'un niveau de détail à l'autre.
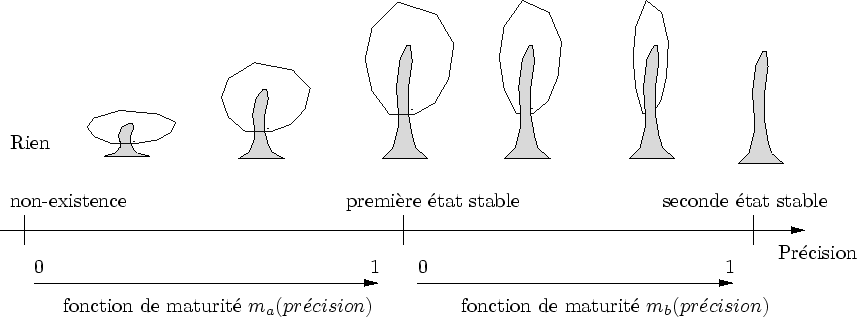\begin{figure}\begin{center} \input{arbre_vie.pstex_t}\end{center}\end{figure}

7.3.3.3 La valse des maturités

La figure 7.17 met en évidence deux types de transitions guidés par deux maturités différentes $m_a(pr\acute{e}cision)$ et $m_b(pr\acute{e}cision)$:

Comme le procédé est récursif sur 3 niveaux, ces deux transitions sont appliquées aux mêmes amplifieurs (cf. figure 7.18). Pour assurer la synchronisation de la disparition d'une enveloppe pendant l'apparition des sous-amplifieurs, on exprime la fonction $m_a$ d'un sous amplifieur en fonction de la fonction $m_b$ de l'amplifieur père : $m_a^{fils}=1-m_b^{p\grave{e}re}$.

Soit $i$ l'ordre de branchement d'un amplifieur, on nomme $m^{i}_a$ et $m^{i}_b$ les maturités des amplifieurs. La figure 7.19 illustre l'évolution de ces différentes maturités en fonction de la précision.

Figure 7.19: Les deux maturités sont déclenchées à des précisions bien particulières, assurant une bonne synchronisation entre les amplifieurs père et fils.
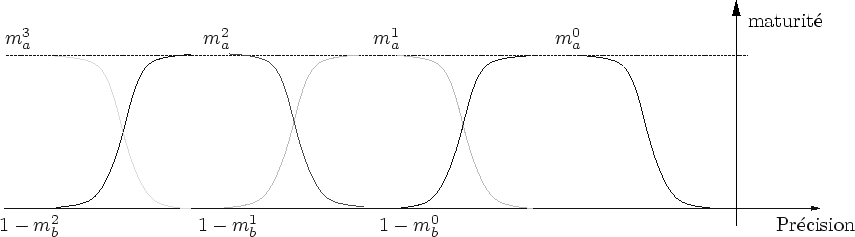
\begin{figure}\begin{center} \input{arbre_mat.pstex_t}\end{center}\end{figure}

7.3.3.4 Conservation de l'espace

Les branches d'un arbre sont générées à partir de la fonction d'enveloppe. Lors de la création de nouveaux amplifieurs, de nouvelles fonctions d'enveloppe sont générées aléatoirement. Elles sont cependant déterminées de façon à remplir approximativement l'enveloppe mère (cf. figure 7.13).

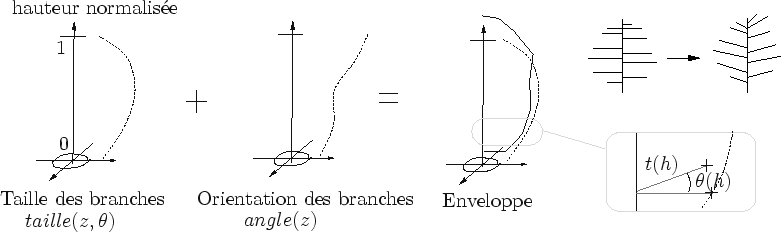
Afin de ne pas effectuer de calcul complexe d'intersection entre une branche et l'enveloppe mère pour trouver la taille de la branche, cette dernière n'est pas directement décrite dans l'espace. Une enveloppe est décrite par deux fonctions : $taille(z,\theta)$ et $angle(z)$ :

$taille(z,\theta)$:
cette fonction décrit la taille d'une branche dont l'origine de l'axe est à une hauteur $z$ sur l'axe du père ;
$angle(z)$:
cette fonction décrit l'inclinaison d'une branche dont l'origine de l'axe est à une hauteur $z$ sur l'axe du père ;

Ainsi, il est facile de reconstruire la fonction enveloppe lors d'un échantillonnage à la volée : il suffit de ``remonter'' le sommet de la branche (déterminer par $taille(z,\theta)$) d'une rotation d'angle $angle(z)$ (cf. figure 7.20).

Figure 7.20: La fonction enveloppe n'est pas donnée explicitement. Elle est générée à la volée grâce à la connaissance des fonctions $taille(z,\theta)$ et $angle(z)$.
\begin{figure}\begin{center} \input{env_angle.pstex_t}\end{center}\end{figure}

7.3.3.5 Générateur d'amplifieurs : Feuilles

Les amplifieurs «feuille» reprennent toutes les fonctionnalités des amplifieurs «branche». Concrètement, la classe décrivant les feuilles hérite de celle décrivant les branches.

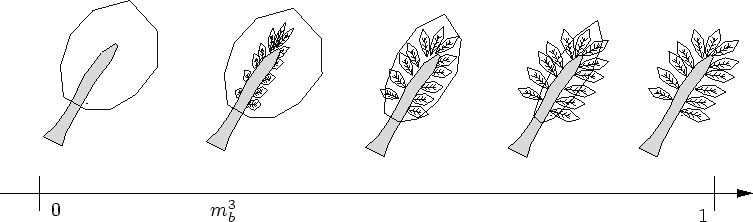
La seule différence est la suivante : lors de la seconde transition (lorsque l'enveloppe disparaît), les feuilles attachées aux troncs apparaissent (cf. figure 7.21). Les feuilles n'ont donc pas d'amplifieur individuel : elles sont simplement ajoutées aux branches les plus fines.

Une feuille est affichée par de simples polygones colorés. C'est ici que s'arrête l'amplification : il faudrait ensuite ajouter les nervures, affiner sa silhouette, et éventuellement faire apparaître les cellules...

Figure 7.21: Les feuilles apparaissent lorsque l'enveloppe des branches d'ordre de branchement maximum disparaissent. D'autres fonctions d'ajout de précision plus sophistiquées aurait pu être utilisées. Néanmoins, les fonctions utilisées ici ont le mérite d'être très simple a implémenté et tout à fait continue. D'un point de vue perceptuel, combinées avec le mouvement de l'arbre, elles sont d'une qualité convenable.
\begin{figure}\begin{center} \input{arbre_str2.pstex_t}\end{center}\end{figure}

7.3.3.6 Générateur d'amplifieurs : Forêt

Une forêt est un amplifieur qui appelle les amplifieurs «branche» plantés verticalement et répartis sur un terrain. Naturellement, chaque arbre est paramétré de façon subtilement différente de façon à briser toute impression de répétitivité. La taille, le nombre de branches, les fonctions d'enveloppe, la couleur : tous ces paramètres peuvent être bruités par des fonctions pseudo-aléatoires. On pourrait appeler ce procédé l'amplification stochastique.

Pour pouvoir reculer encore et voir la forêt de très loin, il faudrait imaginer une façon de l'afficher comme un seul ``individu'', un peu comme le niveau 2D de la prairie (cf. chapitre 4). Cela reste à faire.

7.3.4 Animation

Les fonctions d'animation ont été réalisées en une semaine. Elles reprennent le même concept que celui utilisé pour les prairies. Les récepteurs sont ici aussi la courbure et la direction de courbure de chaque branche.

7.3.4.1 Brise légère

Une petit mouvement aléatoire change la courbure et la direction de chaque branche à tous les niveaux. L'animation est conçue de façon complètement procédurale. Le but des deux utilisateurs de Dynamic Graph était de trouver une fonction mimant de façon acceptable le mouvement des arbres.

Le résultat est à mon goût très satisfaisant. Les résultats montrent encore une fois que l'\oeil est sensible à la complexité du mouvement mais qu'il nous est difficile de déterminer si une animation est réaliste ou non. Comme pour les prairies, c'est la plausibilité qui compte ici.

7.3.4.2 Bourrasque

De même que pour les prairies, une bourrasque impose une direction et une courbure à chaque branche de l'arbre. La seul différence vient du fait que l'orientation du repère tridimensionnel change entre chaque branche. Il est donc nécessaire d'appliquer une rotation pour déterminer la bonne courbure.

De même que pour les brins d'herbe, la taille de chaque branche est modulée à la main pour simuler une taille constante.

7.3.5 Résultats

Nous présenterons tout d'abord le modèle lui-même. Nous décrirons ensuite dans quelle mesure ces stages valident Dynamic Graph en tant qu'outil d'aide à la modélisation multi-échelle.

7.3.5.1 Le modèle

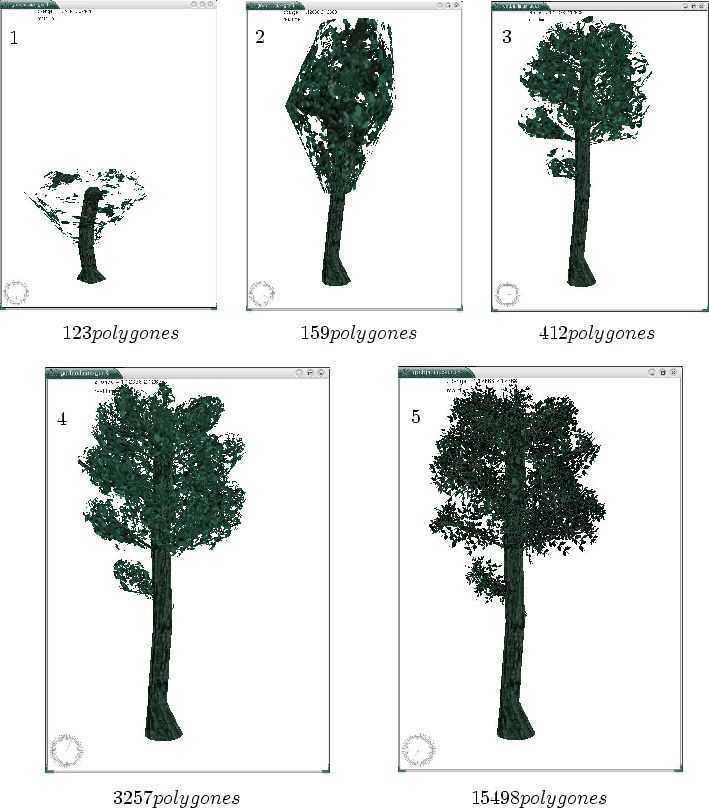
Le modèle prend tout son ampleur lorsqu'il est animé. Je vous convie à télécharger les vidéos sur le site de l'équipe Évasion http://www-evasion.imag.fr/$\sim$Frank.Perbet/dg. La figure 7.22 montre quelques captures d'écran d'un arbre à différentes précisions. La figure 7.23 est une forêt très simple.

Figure 7.22: La précision de cet arbre varie, à titre illustratif, de façon uniforme et indépendamment du point de vue. On remarque ainsi les différents niveaux de détail : trois niveaux d'enveloppes imbriquées laissent ensuite place aux feuilles. Lorsque l'arbre est très loin, il s'enterre dans le sol : c'est le terrain qui doit alors être texturé de façon à représenter une forêt.
\begin{figure}\begin{center} \input{arbre.pstex_t}\end{center}\end{figure}

Figure 7.23: Plusieurs arbres à différentes précisions.
\begin{figure}\begin{center} \input{foret.pstex_t}\end{center}\end{figure}

Le coefficient $Qualit\acute{e} \times Rapidit\acute{e}$ du modèle est acceptable. Néanmoins, pour un affichage temps-réel, il faut vraiment sacrifier la qualité. Durant la création de ce modèle, le soucis de performance n'était pas prioritaire. Il me semble qu'un facteur d'approximativement $10$ peut être gagné par une seconde implémentation plus soucieuse de l'efficacité.

7.3.5.2 Validation de Dynamic Graph

Lors de l'utilisation de Dynamic Graph durant ce stage, certains points intéressants ont été soulevés par les deux étudiants. Tout d'abord, les différents outils d'aide à la modélisation se sont révélées globalement très utiles :

En revanche, les mesures d'occupation mémoire et de temps de calcul n'ont pas été utilisées. Il est probable que ces outils soient plus utiles dans le cas de scènes plus complexes comprenant plusieurs amplifieurs.

Ce stage a aussi été l'occasion de changer un peu Dynamic Graph lui-même. Mis à part les innombrables bogues, ces deux mois ont beaucoup enrichi le dialogue entre Dynamic Graph et le modèle. Avant le début du stage, la seule fonction d'échange (cf. sous-section 5.2.1) était la fonction de création de l'axiome. Très vite, de nouvelles fonctions ce sont révélées nécessaires. Par exemple, des fonctions d'initialisation ont permis de rajouter automatiquement de nouveaux curseurs dans le debugPanel. Ainsi, lorsque l'on charge un modèle, on charge automatiquement les curseurs qui sont associés à ces paramètres. Généralement, Dynamic Graph a beaucoup profité du retour utilisateur durant ces deux mois.

7.3.5.3 Dynamic Graph : un imposteur

Un phénomène curieux s'est produit lors de la conception du modèle d'arbre. Les utilisateurs étaient comme attirés par la précision la plus fine. Une fois les feuilles créées, les niveaux de détail intermédiaires ont été négligés : le plus gros du travail passé dans la modélisation du niveau le plus fin. Je vois différentes explications à ce phénomène :

Dynamic Graph est un outil permettant de mimer le réel. À plusieurs reprise, j'ai insisté pour ne pas utiliser de photo, mais des textures réalisées à la main. Lors de l'animation, il a fallu imposer une modélisation procédurale car les utilisateurs étaient séduits par des simulations physiques qu'il était impossible de réaliser en si peu de temps. Le réalisme, ainsi que ``le niveau le plus fin'', semble attirer notre concentration. Dynamic Graph est à ce titre assez dérangeant car il renvoie à la synthèse d'image une identité que, peut-être, elle ne s'avoue pas : celle d'un imposteur.

next up previous contents
Next: 8. Conclusion Up: main Previous: 6. Dynamic Graph :
Frank Perbet
2004/04/25