6. Dynamic Graph : génération

Nous reprenons ici les concepts expliqués en 5 en les abordant sous un angle plus technique. Plus précisément, nous décrirons les algorithmes mis en $\oe$ uvre pour manipuler l'arbre d'évaluation. Les critères d'arrêt de précision et de visibilité feront l'objet d'une attention particulière.

6.1 Évaluation

Nous verrons dans cette section les mécanismes complexes mis en $\oe$ uvre durant la génération de l'arbre d'évaluation. Nous verrons ensuite comment Dynamic Graph assure une certaine connaissance des informations anciennes, notamment grâce à l'utilisation d'identifieurs. Nous décrirons enfin l'arbre permanent qui, contrairement à un arbre d'évaluation, contient des informations permanentes. Enfin, nous dresserons un bilan de la méthode d'évaluation et proposerons deux améliorations potentielles.

6.1.1 Génération de l'arbre d'évaluation

La génération de l'arbre d'évaluation est dirigée par l'organiseur, via un visiteur particulier : le générateur. L'évaluation d'un amplifieur est réalisée de façon séquentielle : elle ne se termine qu'après plusieurs phases d'exécution. Pour permettre cela, un dialogue a lieu entre le générateur et un amplifieur : le générateur donne des requêtes auxquelles l'amplifieur essaie de répondre.

6.1.1.1 Organiseur et visiteur

À chaque pas de temps, l'évaluation de la forme est effectuée par la création d'un arbre d'évaluation. La création de cet arbre est rythmée par l'organiseur. D'emblée, on distingue deux sortes d'événements temporels (cf. figure 6.1):

**Figure 6.1:** On appelle *pas de temps* les dates auxquelles une nouvelle observation est calculée. Chaque affichage est le fruit d'une évaluation, laquelle est divisée en *étapes* par l'organiseur.
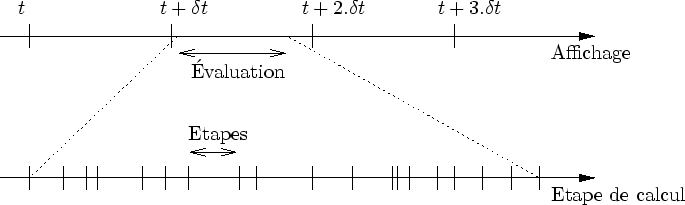$\begin{figure}\begin{center} \input{freq.pstex_t}\end{center}\end{figure}$

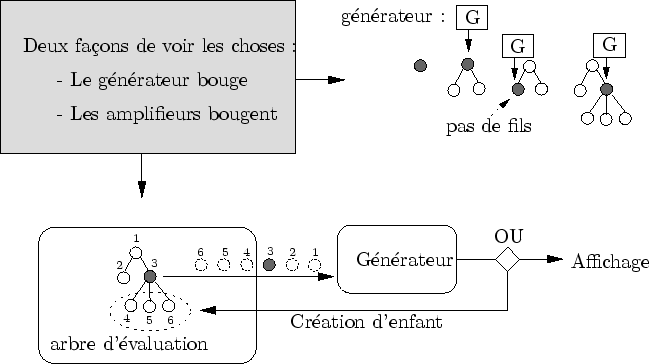
Le générateur est le visiteur qui s'occupe de ``développer'' l'arbre d'évaluation jusqu'à sa complexion. On peut voir un visiteur est une entité qui se déplace sur un graphe pour appliquer un traitement à chaque noeud. Mais dans Dynamic Graph, il est plus intuitif de voir le phénomène ``dual'' : ce sont les noeuds du graphe qui vont visiter le visiteur (cf. figure 6.2).

Cette différence est importante pour décrire l'évaluation avec une architecture en pipe-line. Plutôt que de visualiser un arbre dont les noeuds ne bougent pas, il est préférable d'imaginer qu'un amplifieur, lors de son traitement, entame un sorte de pèlerinage qui le mènera éventuellement à la carte graphique.

**Figure 6.2:** Il est plus facile de rendre compte de l'architecture en *pipe-line* lorsque ce sont les noeuds (les amplifieurs) qui bougent. Attention, ceci n'est qu'une vue de l'esprit. Concrètement, ni le visiteur ni les noeuds ne changent de place en mémoire.
$\begin{figure}\begin{center} \input{visiteur_mode.pstex_t}\end{center}\end{figure}$

6.1.1.2 Évaluation d'un amplifieur

Comme on l'a vu, un amplifieur, lorsqu'il est évalué, ajoute de la précision à la forme. L'organiseur s'occupe de lancer le calcul des amplifieurs via le visiteur générateur. Afin de bien contrôler l'évaluation, l'organiseur reprend la main entre deux évaluations. Ceci est essentiel pour assurer un certain parallélisme entre le processeur central et la carte graphique (nous verrons en section 6.3 pourquoi un tel parallélisme est nécessaire).

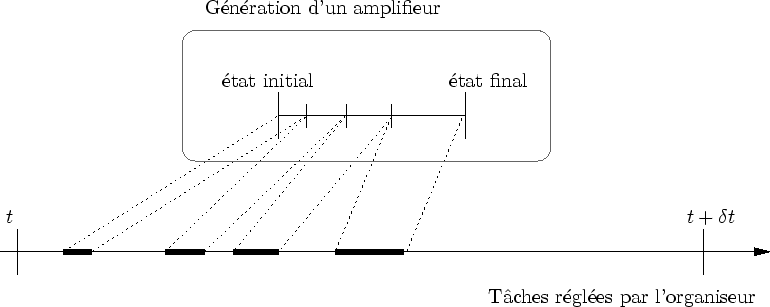
Comme toute action sur un ordinateur, l'évaluation d'un amplifieur n'est pas instantanée et il faut un certain nombre de cycles d'horloge pour que le processeur la termine. Lorsqu'un amplifieur est construit, il est dans son état initial : seule l'initialisation de l'évaluation a lieu. Lorsque l'évaluation est terminée, l'amplifieur est dans son état final : il a terminé tous ses calculs.

**Figure 6.3:** L'organiseur cadence le générateur pour que celui-ci évalue un amplifieur en plusieurs fois. En conséquence, l'organiseur reprend non seulement la main à la fin d'une évaluation, mais éventuellement plusieurs fois durant une même évaluation.
$\begin{figure}\begin{center} \input{eval_seq.pstex_t}\end{center}\end{figure}$

6.1.1.3 Évaluation séquentielle

Cette évaluation séquentielle est mise en $\oe$ uvre pour permettre à un amplifieur d'attendre la fin de tâches parallèles sans bloquer le processeur courant. En effet, imaginons que l'évaluation d'un amplifieur requiert une certaine information qui n'est pas encore prête : l'amplifieur devient alors bloquant. Plutôt que d'attendre inutilement, l'amplifieur peut rendre la main à l'organiseur qui va aller ``stimuler'' d'autres amplifieurs non-bloquants.

En théorie, Dynamic Graph est donc parfaitement conçu pour tourner en parallèle sur plusieurs processeurs. Pourtant, ce n'est pas ce type de parallélisme qui est visé en premier. Les évaluations séquentielles sont initialement prévues pour assurer une bonne synchronisation entre le processeur principal et le processeur graphique (cf. section 6.3).

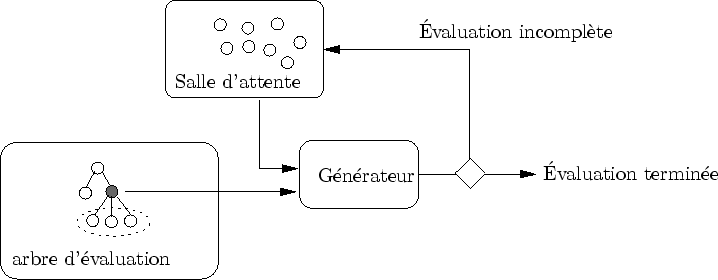
Les amplifieurs bloquants sont référencés dans une liste appelée la salle d'attente (cf. figure 6.4). Elle réinjecte les amplifieurs qui se sont débloqués vers le générateur. Une priorité est attribuée aux amplifieurs débloqués afin de libérer plus vite d'autres amplifieurs.

Si tous les amplifieurs sont bloquants, l'organiseur attend. Il est donc, par exemple, plus important de libérer un amplifieur dont on estime que les enfants sont nombreux. En effet, tout nouvel amplifieur est par défaut non bloquant. Plus le nombre d'amplifieurs non-bloquants est grand, plus l'organiseur peut organiser son travail efficacement. Remarquez que ce mécanisme permet de diminuer les durée de blocage, mais non de les supprimer.

**Figure 6.4:** La salle d'attente récupère les références des amplifieurs dont l'évaluation est incomplète et attend le bon moment pour les remettre dans le circuit.
$\begin{figure}\begin{center} \input{recycleur.pstex_t}\end{center}\end{figure}$

6.1.1.4 Requêtes du visiteur

On peut formaliser l'échange complexe qui a lieu entre un visiteur et un amplifieur de la façon suivante : pour déclencher l'évaluation d'un amplifieur, le visiteur lance une requête. Lorsque l'amplifieur lui rend la main, le visiteur vérifie si la requête est satisfaite. Dans le cas contraire, il envoie cet amplifieur dans la salle d'attente.

Différentes sortes de requêtes sont possibles. La plus courante est la requête de complexion : "Dessine la forme ou génère des enfants si nécessaire". D'autres requêtes sont possibles. Par exemple, le générateur peut forcer certains calculs : "génère tes enfants quoiqu'il arrive".

On peut représenter les différentes fonctions qu'un amplifieur peut réaliser par un graphe de dépendance des résultats qu'il peut produire (cf. figure 6.5). Au cours d'une même observation, l'amplifieur se souvient des fonctions qu'il a déjà exécutées. De cette façon, lors d'une reprise des calculs, l'évaluation peut reprendre là où elle s'était arrêtée.

**Figure 6.5:** Au contact d'un visiteur, un amplifieur peut exécuter différentes fonctions. Celle-ci dépendent les unes des autres. Par exemple, l'affichage ne peut être effectué qu'après le calcul de l'animation.
$\begin{figure}\begin{center} \input{node_dep.pstex_t}\end{center}\end{figure}$

Généralement, le générateur demande la requête de complexion à tous les amplifieurs. La complexion d'un amplifieur entraîne souvent la création de nouveaux amplifieurs qui doivent être évalués à leur tour. Lorsque tous les amplifieurs satisfont la requête de complexion, l'évaluation est terminée.

6.1.2 Mémoire et identifiant

Dans Dynamic Graph, chaque arbre d'évaluation connaît son ancêtre (notamment pour permettre l'optimisation par cohérence temporelle). Ceci est réalisé grâce au tampon d'arbres et aux identifiants attribués à chaque noeud. Chaque amplifieur a une date de naissance et de mort définissant sa durée de vie, notamment utilisée pour stocker des informations sur une longue durée.

6.1.2.1 Tampon d'arbres

Le tampon d'arbres stocke les

derniers arbres d'évaluations.

est fixé par le créateur ou l'application, selon les besoins de l'un ou de l'autre. Cette valeur peut être modifiée dynamiquement durant l'exécution du programme.

Son implémentation est basé sur l'utilisation de ``tableaux rotatifs''. Ces tableaux sont tout simplement des tableaux normaux dont l'accès est rendu cyclique en prenant les index modulo

Lorsque le programme débute, les premières cases du tableau, initialement vides, sont successivement remplies par un arbre d'évaluation. Lorsque le tableau est plein, les cases les plus vieilles sont libérées pour laisser place aux nouveaux arbres.

Chaque arbre d'évaluation est connecté à son ancêtre (l'arbre du pas de temps précédent). La connexion est réalisée dans les deux sens, ce qui signifie que chaque arbre est connecté à son ancêtre et à son successeur (s'ils existent).

6.1.2.2 Identifiant global

**Figure 6.6:** Chaque amplifieur de chaque arbre d'évaluation stocké dans le tampon d'arbres a connaissance de son successeur et de son ancêtre. Ceci lui permet d'avoir accès aux informations à des temps différents (généralement passés).
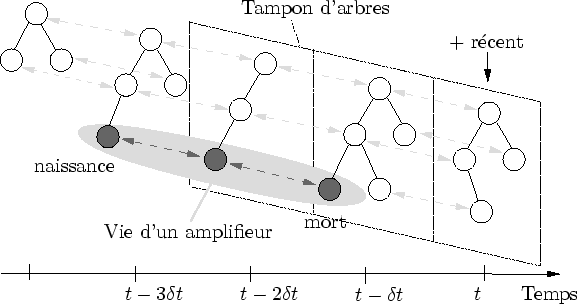$\begin{figure}\begin{center} \input{ancetre.pstex_t}\end{center}\end{figure}$

Lorsque l'on dit qu'un arbre est connecté à son ancêtre, cela signifie que chacun de ses noeuds (i.e. amplifieurs) est connecté à son noeud ancêtre (cf. figure 6.6). Cette connexion est réalisée durant la création d'un nouvel arbre (c'est-à-dire durant une nouvelle évaluation). Le principe est simple : chaque noeud a un identifiant global le distinguant de tous les autres noeuds d'un même arbre. Lorsqu'un noeud est créé, il vérifie si un noeud du même identifiant existe dans l'arbre précédent : s'il existe, la connexion est créée. Ceci baigne chaque amplifieur dans une structure de liste doublement chaînée.

Une recherche d'identifiant global dans un arbre est une opération dont le coût n'est pas négligeable. Si l'on considère que l'accès à un fils est réalisé en coût constant, le coût moyen d'une recherche est proportionnel à la hauteur de l'arbre précédent. La réaliser lors de la création de chaque nouveau noeud grèverait considérablement les performances. L'utilisation d'identifiant local permet de palier ce problème.

6.1.2.3 Identifiant local

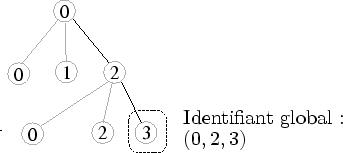
Un identifiant local permet de distinguer un amplifieur parmi ces frères. Concrètement, un identifiant local est un entier non signé. Un identifiant global est une liste d'identifiants locaux décrivant le chemin à suivre pour aboutir au noeud en question (cf. figure 6.7). Chaque noeud de l'arbre contient un conteneur vers ces noeuds fils. Ce conteneur est un conteneur associatif [D'A02] dont la clef (unique) est l'identifiant local. Accéder au fils $i \in \mathcal{N}$ revient donc à chercher l'existence de cette clef dans le conteneur associatif.

**Figure 6.7:** Un identifiant global est une liste d'identifiants locaux représentant le chemin de la racine à l'amplifieur identifié. Un identifiant local est unique parmi les identifiant des amplifieurs frères. Un identifiant global est unique parmi les identifiant des amplifieurs de l'arbre.
$\begin{figure}\begin{center} \input{id.pstex_t}\end{center}\end{figure}$

Pour les raisons de performance identifiées plus haut, les identifiants locaux sont utilisés pour faire des recherches relatives. Pour comprendre intuitivement le mécanisme, on peut le comparer aux chemins de fichiers sous UNIX. Il est en effet souvent plus efficace d'accéder à un fichier par un chemin relatif comme :

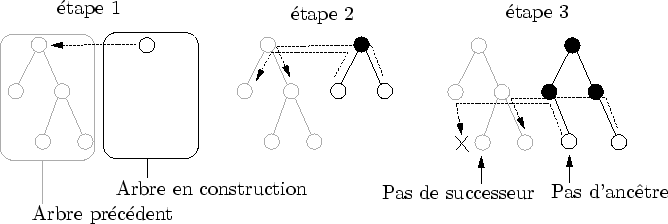
La recherche de l'ancêtre est réalisée au cours de l'évaluation. Elle est initialisée avec la racine du nouvel arbre : celui-ci est spécifiquement connecté à la racine de l'arbre précédent par l'organiseur. Ensuite, chaque nouvel amplifieur a pour ancêtre (au sens temporel) "le fils de l'ancêtre de son père" (cf. figure 6.8). Comme les connexions sont réalisées au fur et à mesure, on est assuré que le père d'un amplifieur connaît déjà son ancêtre.

**Figure:** L'ancêtre d'un noeud est "le fils de l'ancêtre de son père". Cette formulation ne fait intervenir qu'une recherche d'identifiant local, c'est-à-dire la recherche d'un fils particulier parmi ses frères. Nous verrons en 7.2 que le coût de cette recherche dépend des choix que fait le créateur. Dans le meilleur des cas, elle est effectuée en coût constant.
$\begin{figure}\begin{center} \input{connection_ancetre.pstex_t}\end{center}\end{figure}$

6.1.2.4 Destruction

À chaque pas de temps, lorsque le tampon d'arbres est plein, l'arbre le plus vieux est détruit. C'est un visiteur particulier qui s'occupe de ça : le destructeur. Celui-ci parcourt l'arbre des feuilles vers la racine en utilisant le retour d'un parcours en profondeur d'abord.

Il détruit tous les fils de l'amplifieur qu'il visite (la racine a un traitement particulier). De plus, si l'amplifieur n'a pas de successeur, il appelle sa fonction de mort. Si l'amplifieur à un successeur, il supprime proprement ce lien (dans les deux sens).

6.1.2.5 Vie et mort

La figure 6.6 montre la vie et la mort d'un amplifieur. La naissance est par définition une construction sans ancêtre et la mort une destruction sans successeur. Lors de la naissance (resp. de la mort) d'un amplifieur, un constructeur (resp. un destructeur) spécial est appelé.

Cette fonctionnalité permet d'initialiser de l'amplifieur. Par exemple, une texture peut être allouée lors de la naissance et désallouée lors de la mort. Plus généralement, la naissance et la vie d'un amplifieur permet de stocker n'importe quelle information mortelle pendant plusieurs pas de temps. L'information mortelle dure plus longtemps que les informations éphémères qui sont stockées dans un amplifieur : celles-ci sont accessibles

pas de temps ou

est la taille du tampon d'arbres En revanche, l'information mortelle dure moins longtemps que l'information permanente qui est décrite dans la sous-section suivante.

6.1.3 Arbre permanent

Les arbres d'évaluation, très dynamiques, sont complétés par un arbre permanent, représentant en quelque sorte la partie statique de l'évaluation. Il sert à stocker toutes les informations qui ne sont pas animés et ne nécessitent donc pas d'être recalculer à chaque pas de temps. Cet arbre ne dépend pas de l'observation et peut donc être très grand ; en conséquence, un effort particulier est fait pour maintenir sa taille la plus petite possible.

6.1.3.1 Description

Les informations stockées dans les noeuds sont très volatiles : leur durée de vie est celle de la taille du tampon d'arbres. Afin de donner la possibilité de stocker des informations de façon permanente, un arbre statique complète le tampon d'arbres dynamiques. Dans le cas de la prairie, par exemple, la courbure et la direction d'un brin d'herbe sont stockées dans l'arbre dynamique, alors que la couleur du brin d'herbe est stockée dans l'arbre permanent. Il permet d'associer à des amplifieurs particuliers des données supplémentaires. Il est appelé l'arbre permanent.

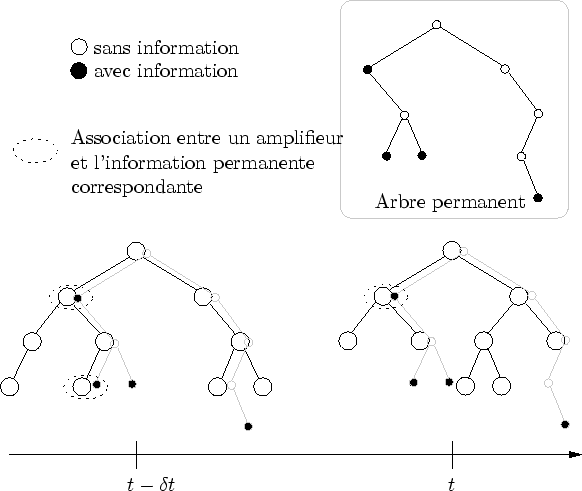
Les noeuds qui le composent, parce qu'ils représentent la partie permanente de l'information, sont appelés amplifieurs permanents. On peut représenter cet arbre comme un arbre partiellement superposable aux arbres d'évaluations mais beaucoup moins dense que ceux-ci (cf. figure 6.9).

**Figure 6.9:** Cette figure montre l'arbre dynamique à deux pas de temps successif avec, en grisé, l'arbre permanent. L'arbre permanent ne change pas dans le temps. Les données permanentes sont associées à un amplifieur qui, à un instant donné, peut exister ou non. Certains noeuds de l'arbre permanent sont vides et ne servent qu'à atteindre des noeuds non vides.
$\begin{figure}\begin{center} \input{arbre_special.pstex_t}\end{center}\end{figure}$

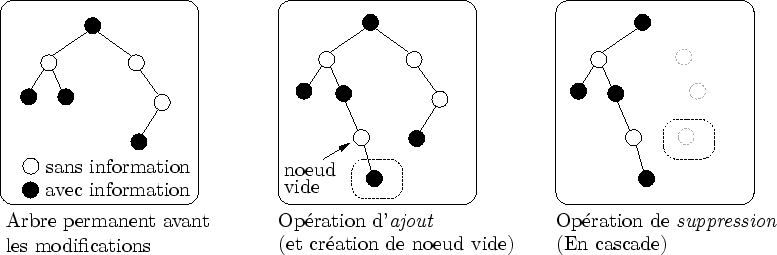
Rappelons que l'arbre d'évaluation est potentiellement infini. Seuls les critères d'arrêt qu'engendre une observation permet de limiter son expansion. L'arbre permanent n'est a priori pas sujet à cette restriction : les informations qu'il contient sont permanentes, que l'amplifieur soit observé ou non. Elles ne peuvent être supprimées que par une intervention explicite (soit du créateur, soit de l'organiseur).

6.1.3.2 Taille minimale

Si chaque amplifieur demande un homologue dans l'arbre permanent, la taille de celui-ci explose. Son utilisation doit donc rester exceptionnelle : seul quelques amplifieurs spéciaux peuvent l'utiliser.

De plus, afin de minimiser la mémoire occupée par l'arbre permanent, il est nécessaire de garder sa taille la plus petite possible. Pour cela, on s'assure que ce dernier est le plus petit graphe contenant tous les amplifieurs permanents (cf. figure 6.10). Concrètement, cela évite de garder en mémoire des informations concernant une forêt dans une zone désertique.

**Figure 6.10:** L'arbre permanent, lors d'ajout ou de suppression d'informations, rajoute ou supprime des noeuds vides afin de garder la taille minimum requise pour accéder à toutes les informations permanentes. Remarquons qu'une conséquence de cela est que chaque feuille de l'arbre contient toujours de l'information.
$\begin{figure}\begin{center} \input{operation_special.pstex_t}\end{center}\end{figure}$

6.1.3.3 Amplifieur enrichi

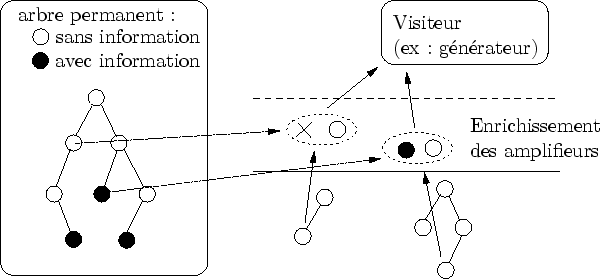
Lorsqu'un visiteur parcourt l'arbre d'évaluation, il parcourt en même temps l'arbre permanent. Ainsi, lorsqu'un amplifieur s'apprête à être visité par le générateur, il est enrichi d'une référence vers ses éventuelles informations permanentes (cf. figure 6.11).

**Figure 6.11:** Avant d'être traité par le visiteur, l'amplifieur est enrichi de ses informations permanentes (si celles-ci existent).
$\begin{figure}\begin{center} \input{enrichissement.pstex_t}\end{center}\end{figure}$

Lors de l'évaluation de l'amplifieur, le générateur met à disposition de celui-ci la zone de mémoire permanente. Elle est utilisée pour stocker des informations importantes. Dans un jeu, par exemple, cette mémoire peut servir à se souvenir qu'un objet particulier a été déposé ici par le joueur.

6.1.4 Bilan

La structure dynamique de Dynamic Graph permet de représenter des structures en perpétuelles transformations, parfaitement adéquate à une représentation par complexification. Néanmoins, on est en droit de se demander si cette structure n'est pas trop dynamique. Une nouvelle conception du tampon d'arbres local semblerait apporter une réponse. Enfin, nous verrons que le parcours de l'arbre d'évaluation dépend de l'échelle d'observation et limite ainsi les zooms très grands ; nous verrons comment la méthode de congélation, apporterait une solution partielle.

6.1.4.1 Dynamisme de la structure

La complexification entraîne une vision très dynamique de la forme affichée : celle-ci, en plus de son animation, s'adapte sans cesse aux mouvements de l'observateur. Pour représenter une forme aussi mouvante, il est nécessaire d'utiliser une structure qu'il est facile de mettre à jour. Dynamic Graph choisit une solution extrême : à chaque pas de temps, tout est régénéré. C'est un pari risqué : tout sur la génération à la volée.

La souplesse de la structure choisie est un avantage. La conception d'un algorithme traitant de scènes statiques a souvent quelques difficultés lorsqu'il faut passer à l'animation^6.1. Dynamic Graph prend le parti inverse : la conception est entièrement pensée pour des structures animées. Lors de la modélisation de structure statique avec Dynamic Graph, il est toujours possible d'utiliser l'optimisation par cohérence temporelle. Nous verrons dans le chapitre 7 comment les informations éphémères, mortelles et permanentes peuvent être utilisée pour cela.

6.1.4.2 Régénération vs. modification

On peut tout de même reprocher à Dynamic Graph de faire beaucoup de calculs inutils lors de la modélisation de scènes statiques. Notamment, il devient inutile d'assurer la liaison entre un ancêtre et son successeur. Dynamic Graph propose généralement plus que ce que désire le créateur : c'est une façon d'être sûr que ce dernier ne se sente pas limité. En revanche, cela entraîne un coût supérieur à l'approche classiquement utilisée : la modification d'une structure statique.

Il est très délicat d'argumenter de façon générale des avantages et des inconvénients d'une structure statique (modifiée) ou d'une structure dynamique (générée à la volée). Ceci dépend notamment des fonctions que code le créateur au sein d'un générateur d'amplifieurs : certaines supportent très bien les modifications, d'autres moins. Dynamic Graph permet suffisamment de souplesse (grâce aux informations mortelles et permanentes) pour laisser le choix au créateur. Néanmoins, le comportement par défaut est celui de la régénération.

La modification est souvent plus efficace que la régénération lorsqu'il existe une forte similarité entre deux images (i.e. observation). Cette contrainte n'est pas toujours assurée. Même si l'observateur évolue très souvent de façon continue, il arrive fréquemment qu'il se déplace trop vite et que les opérations de modification deviennent ainsi trop coûteuses. La régénération est plus souple à ce niveau et permet généralement des mouvements de caméra moins contraints.

6.1.4.3 Travaux futurs : tampon d'arbres local

L'une des plus grandes limites de l'algorithme actuel est l'impossibilité d'assigner des fréquences de mise à jour différentes pour chaque générateur d'amplifieurs. Une telle fonctionnalité est similaire à celle de la plateforme de simulation OpenMask [Mar02] ou aux MTG [GC98]. Elle permettrait par exemple d'insérer des objets statiques avec une fréquence de mise à jour nulle. Une telle structure semble réalisable grâce à une conception plus locale du tampon d'arbres (cf. figure 6.12).

**Figure 6.12:** Pour que chaque noeud d'un graphe se souvienne de son ancêtre, deux structures sont possibles. La structure globale de Dynamic Graph stocke arbres représentant les dernières observations. La structure locale ne représente qu'un seul arbre, mais au sein de chaque noeud, amplifieurs sont stockés (représentant les dernières observations).
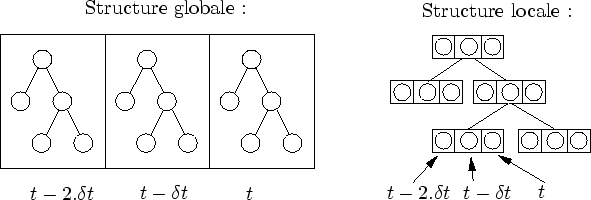$\begin{figure}\begin{center} \input{mode_ancetre.pstex_t}\end{center}\end{figure}$

Cette conception est à vrai dire très séduisante. Elle permettrait aux visiteurs d'ignorer les noeuds n'ayant pas besoin de mise à jour. De plus, la recherche de l'ancêtre serait alors immédiate. Il serait très intéressant de coder cette solution et de la confronter à l'implémentation actuelle.

6.1.4.4 Travaux futurs : la congélation

La régénération à chaque pas de temps de tout l'arbre d'évaluation entraîne un coût qui dépend de l'échelle d'observation : plus la scène est précise, plus l'arbre est grand et plus le temps de parcours augmente. Même si l'arbre à son niveau grossier est très mince, il faut au moins parcourir toute la hauteur. Ceci pose problème pour les très grandes variations d'échelle. En fait, nous n'avons pas pu observer ce phénomène car nous avons été limités par les problèmes d'imprécisions numériques. En effet, lorsque la caméra se rapproche trop d'un objet, la taille des détails observés et trop petite pour être représenté sur nombre constant de bits (typiquement

Ce n'est pas parce qu'un problème est caché par un autre que l'on peut l'ignorer, voyons les solutions qui s'offrent à nous. On peut envisager de congeler la partie grossière de l'arbre en une sorte ``d'amplifieur axiome compressé'' (cf. figure 6.13). Ce dernier pourrait, par exemple, représenter la partie congelée (forcément très lointaine) par un imposteur. Mais alors, l'animation des parties grossières du graphe seront ignorées. Cette approche ne pose pas de problème pour les zooms ``allé simple'' ou l'observateur se rapproche sans cesse sans jamais reculer beaucoup.

**Figure 6.13:** Lorsque le graphe devient trop haut, on pourrait ``compresser'' la partie haute.
$\begin{figure}\begin{center} \input{freeze.pstex_t}\end{center}\end{figure}$

On peut imaginer que les générateurs d'amplifieurs sachent non seulement ajouter de la précision en créant des amplifieurs fils, mais aussi enlever de la précision en créant leur amplifieur père^6.2. On touche ici à la limite intrinsèque de la complexification : celle-ci ajoute de l'information mais ne sait pas en enlever. Les langages descriptifs simples utilisés dans les méthodes de simplification autorisent la diminution de la précision. Mais dans le cas du langage descriptif complexe de Dynamic Graph, je vois mal comment une telle prouesse peut être réalisée...

6.2 Précision

La fin de ce chapitre est dédié aux critères d'arrêt de la génération de l'arbre d'évaluation de Dynamic Graph: la précision et la visibilité. Dans cette section, la précision sera définie. Ensuite, nous ferons une première incursion du côté de la modélisation et nous présenterons la maturité comme une transformation pratique de la précision. Enfin, nous conclurons sur ces deux concepts avant de passer au second critère d'arrêt : la visibilité

6.2.1 Précision

Nous définirons tout d'abord la précision de manière formelle. Nous la reformulerons ensuite de façon approximative, efficace et suffisante aux besoins de Dynamic Graph. Nous verrons enfin comment la précision intervient lors de la génération de l'arbre d'évaluation.

6.2.1.1 Définition théorique

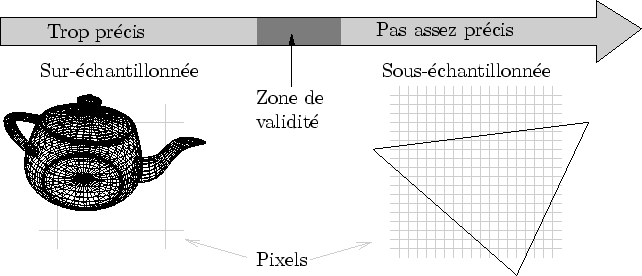
La précision est une notion très délicate à définir. Nous avons vu en 2.1 qu'un signal pouvait être sur-échantillonné ou bien sous-échantillonné. Dans Dynamic Graph, la précision est représentée par un nombre réel mesurant la qualité de l'échantillonnage (cf. figure 6.14).

**Figure 6.14:** La précision est représentée par un réel. Une valeur positive signifie que la forme est sous-échantillonnée. Une valeur négative signifie que la forme est sur-échantillonnée. La valeur nulle représente l'échantillonnage idéal. Le but du jeu est ici de se rapprocher au maximum de la valeur nulle.
$\begin{figure}\begin{center} \input{mesure_precision.pstex_t}\end{center}\end{figure}$

Plus formellement, on peut considérer qu'un amplifieur $\mathcal{A}$ affiché envoie un ensemble de primitives graphiques :

$\begin{displaymath} \mathcal{P}_{\mathcal{A}}=\{primitives\:graphiques\:envoy\acute{e}es\:par\:\mathcal{A}\} \end{displaymath}$

Pour chaque primitive graphique $p \in \mathcal{P}_{\mathcal{A}}$ , on peut déterminer la surface de l'écran

qu'elle va remplir en nombre de pixels. Cette valeur peut être infiniment grande (on ne considère pas le view frustrum culling). Elle peut être infiniment petite (pour un triangle infiniment petit par exemple).

Soit $S_{ideale}$ la taille de triangle considérée comme parfaite (cf. [WW03]). Cette valeur dépend notamment de l'application visée. Pour fixer les idées, pour une qualité maximum, on a $S_{ideale} \simeq 10 \times 10 \: pixels$ .

Pour chaque primitive graphique $p \in \mathcal{P}_{\mathcal{A}}$ , on peut alors exprimer l'aire ``normalisée'' : $S(p)=\frac{s(p)}{S_{ideale}}$ . Cette fonction vaut

lorsque la primitive a la taille idéale.

On peut calculer l'aire normalisée moyenne de toutes les primitives graphiques envoyées à la carte graphique par un amplifieur :

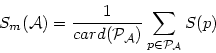
$\begin{displaymath} S_m(\mathcal{A})=\frac{1}{card(\mathcal{P}_{\mathcal{A}})}\sum_{p \in \mathcal{P}_{\mathcal{A}}} S(p) \end{displaymath}$

Le but de Dynamic Graph est donc de générer des amplifieurs tels que $S_m(\mathcal{A}) = 1$ . Afin de bien résoudre cette équation, il est préférable de mieux conditionner l'équation en prenant son logarithme : $log_2(S_m(\mathcal{A})) = 0$ .

Remarquons que lorsque les primitives sont deux fois plus grandes que la taille idéale, on a :

6.2.1.2 En pratique

En pratique, le calcul précis de la surface de chaque primitive est inutilement coûteux. En effet, l'expérience montre qu'une grossière estimation est largement suffisante pour obtenir des résultats satisfaisants.

$S_{bb}$ est la surface projetée d'une boîte englobante sphérique de l'amplifieur. Comme nous le verrons dans le chapitre suivant, la boîte englobante est spécifiée par le créateur lors de la modélisation. $C_{cr\acute{e}ateur} \in [0,1]$ est un coefficient de calibration qui reflète la discrétisation de l'amplifieur. Par exemple, un maillage sphérique très échantillonné aura un coefficient $C_{cr\acute{e}ateur}$ inférieur à

. À l'opposé, un maillage sphérique peu échantillonné aura un coefficient $C_{cr\acute{e}ateur}$ proche de

**Figure 6.15:** L'aire projetée $S_{bb}$ de la boîte englobante d'un objet donne une idée approximative de la taille qu'il occupe sur l'écran. En diminuant le coefficient $C_{cr\acute{e}ateur}$ , on peut prendre en compte le fait que l'objet a beaucoup de polygones (ou qu'il est texturé avec une image de grande résolution). Dans le cas de l'amplifieur 2D de la prairie, la valeur $C_{cr\acute{e}ateur}$ est petite car le polygone est texturé (ce qui, visuellement, est équivalent à une subdivision plus fine du polygone).
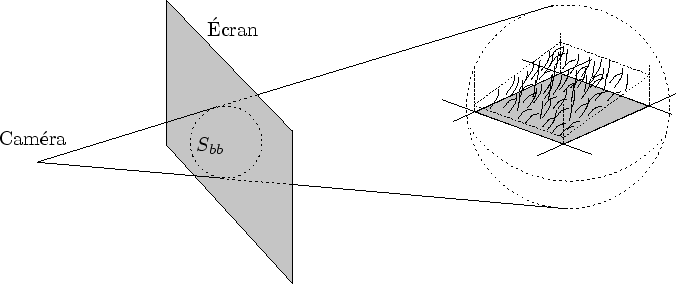$\begin{figure}\begin{center} \input{sbb.pstex_t}\end{center}\end{figure}$

Ces deux coefficients sont donnés par le créateur pour chaque générateur d'amplifieurs (cf. figure 6.15). C'est donc ce dernier qui spécifie entièrement la fonction de précision. Par expérience, la gène occasionnée par la détermination d'une boîte englobante sphérique et du coefficient $C_{cr\acute{e}ateur}$ sont minimes (en tout cas négligeable par rapport au reste du modèle).

6.2.1.3 Critère d'arrêt

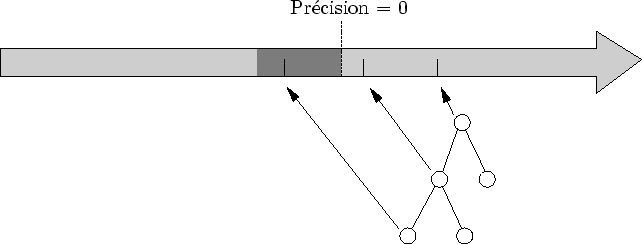
La fonction $precision(\mathcal{A})$ est celle utilisée dans le critère d'arrêt de précision de chaque amplifieur $\mathcal{A}$ . Le test de précision est très simple : si la précision est négative, cela signifie qu'elle est suffisante (cf. figure 6.16).

**Figure 6.16:** Les amplifieurs génèrent des fils tant qu'ils n'atteignent pas la première précision négative.
$\begin{figure}\begin{center} \input{arret_precision.pstex_t}\end{center}\end{figure}$

Remarquons, qu'une simple variation de $S_{ideale}$ permet de diminuer la précision (et donc la qualité) tout en augmentant les performances (moins de géométrie est générée). Dynamic Graph propose donc un contrôle total sur le coefficient $Qualit\acute{e} \times Rapidit\acute{e}$ .

Des contrôles plus fins sont permis : la valeur de $S_{ideale}$ peut varier par générateur d'amplifieurs. Ceci permet la calibration relative de modèles d'origine différente lors de leur mise en commun.

6.2.2 Transition et maturité

Nous verrons ici comment la précision est transformée en une valeur utilisable par le créateur : la maturité. La maturité est une sorte de normalisation de la précision idéale pour interpoler continûment l'ajout de détail d'un amplifieur. Nous verrons deux versions de la maturité : synchrone et asynchrone.

6.2.2.1 La précision : une variable continue

Le rôle que joue la précision dans les critères d'arrêt est discret : l'amplifieur génère des fils ou non. La nature continue de la précision est utilisée pour assurer le passage continu d'un amplifieur à ses amplifieurs fils. Pour reprendre le vocabulaire utilisé dans le chapitre 4, les transitions entre niveaux de détail doivent être continues.

Dynamic Graph accorde une grande importance à cette continuité. De nombreux critères plus ou moins importants sont garants du ``bon'' déroulement d'une transition. Nous plaçons la continuité parmi les plus importants : le moindre popping visuel détériore très notablement la qualité du rendu.

Soyons clairs, Dynamic Graph n'assure pas automatiquement ces transitions. Il propose simplement au créateur un coefficient d'interpolation qui permettra à ce dernier d'ajouter la précision continûment. Ce coefficient est appelé maturité. Lorsque la maturité est nulle, les détails codés par l'amplifieur sont indiscernables. Lorsque la maturité vaut un, l'amplifieur a ajouté toute la précision dont il était capable.

Remarquons qu'il est essentiel que lors de l'apparition d'un amplifieur fils, la maturité de ce dernier soit nulle. Dans le cas contraire, on distinguera un pop de la forme car celle-ci sera subitement enrichie.

6.2.2.2 Maturité synchrone

**Figure 6.17:** Avec la maturité synchrone, un amplifieur passe d'une maturité à par une simple fonction croissante sur l'*intervalle d'amplification* $[ - \alpha ,0]$ . Lorsque l'observateur se rapproche, la précision augmente et la maturité ``glisse'' vers sa valeur maximum.
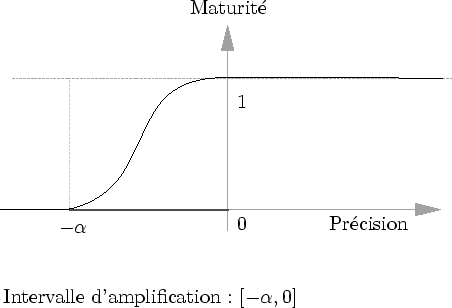$\begin{figure}\begin{center} \input{maturite_synchrone2.pstex_t}\end{center}\end{figure}$

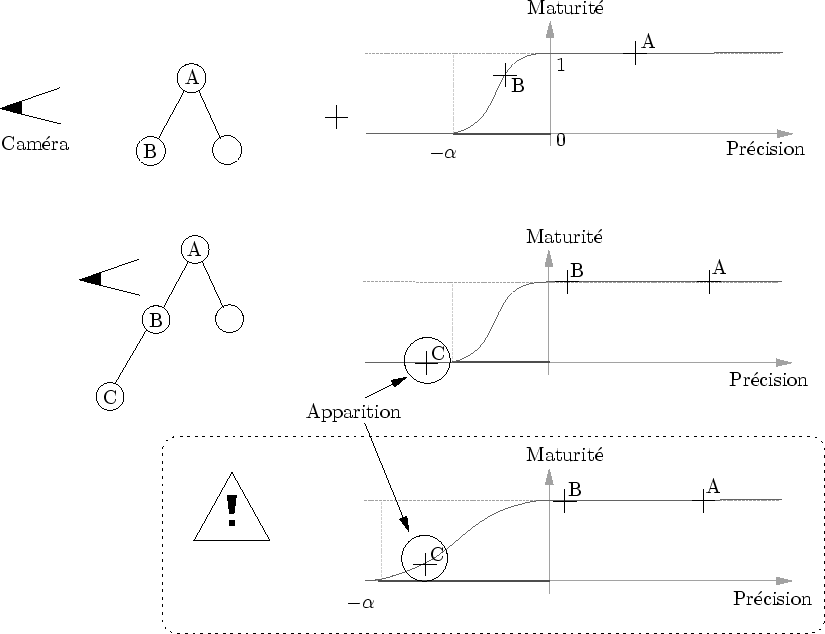
La première définition de la maturité qui vient à l'esprit est une simple transformation de la précision $maturite=f_{maturite}(precision)$ (cf. figure 6.17). Cette fonction est principalement définie par $\alpha$ déterminant la taille de l'intervalle d'amplification.

**Figure 6.18:** Lorsque la caméra se rapproche, un nouvel amplifieur naît. Si tout se passe bien, la précision de celui-ci sera suffisamment faible pour que que sa maturité soit nulle. En conséquent, l'ajout de détail est initialement indiscernable. Mais si $\alpha$ est mal réglé par le créateur, un amplifieur peut naître avec une maturité non nulle, ce qui engendrera un ajout soudain de précision.
$\begin{figure}\begin{center} \input{maturite_synchrone.pstex_t}\end{center}\end{figure}$

Cette taille dépend de l'amplifieur et de la précision qu'il couvre. C'est au créateur de régler le coefficient $\alpha$ (par calibrage expérimental). Celui-ci doit-être suffisamment petit sans quoi un amplifieur peut apparaître avec une transition non-nulle (cf. figure 6.18). Ceci entraîne des discontinuités de l'affichage à proscrire absolument. Dans le cas de la prairie, on aura par exemple la représentation 2.5D qui apparaîtra soudainement sur la représentation 2D sans ``pousser'' continûment.

Cette version de la maturité est appelée maturité synchrone car pour une position de la caméra correspond une valeur unique de la maturité pour chaque amplifieur. Le principal problème lié à cette maturité est qu'elle autorise un amplifieur à rester dans des positions intermédiaires (comme

). Or, dans certains cas (cf. sous-section 4.1.3), l'esthétique des positions intermédiaires peut être inférieure à celle des positions de repos (

). Nous en avons vu un exemple pour les états de transition entre 2D et 2.5D dans le cas de prairie. Pour remédier à ce problème, Dynamic Graph propose des transitions asynchrones.

6.2.2.3 Maturité asynchrone

La maturité asynchrone dépend du temps : une fois déclenchée (quelque soit le sens), elle se termine forcément. Pour cela, il faut définir deux valeurs de précision $p_{min}$ et $p_{max}$ telles que :

Le principal problème avec cette technique est que la maturité a de ``l'inertie''. En conséquence, la forme se modifie toujours même lorsque la caméra ne bouge pas. Ceci n'a pas d'importance pour la plupart des objets animés car cela passe inaperçu : l'animation des objets ``cache'' l'animation due à la maturité. En revanche, pour les objets non-animés, cela nuit indéniablement à la qualité de l'effet visuel.

L'astuce ici consiste à faire varier la vitesse $v_{maturite}$ en fonction des mouvements de la caméra (ou tout autre action ``diversive''). Dès que la caméra bouge ``sensiblement'', la vitesse $v_{maturite}$ augmente. En fait, pour détecter les mouvements de la caméra, on peut utiliser la dérivée de la précision :

$\begin{displaymath} \frac{\delta precision(t)}{dt} = \frac{precision(t)-precision(t-\delta t)}{\delta t}. \end{displaymath}$

$\begin{displaymath} maturite(t)=maturite(t-\delta t) + f_{vitesse}(precision(t)-precision(t-\delta t)).\delta t \end{displaymath}$

**Figure 6.19:** Deux exemples de fonction $f_{vitesse}$ . À gauche, la fonction permet deux vitesses : lente pour les faibles variations et rapide pour les grandes variations. À droite, c'est le même principe en plus continu.
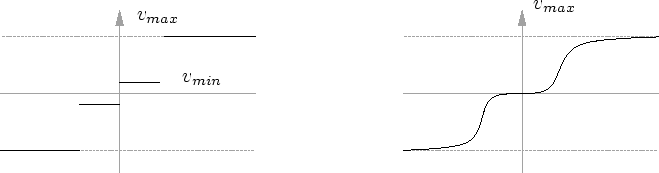$\begin{figure}\begin{center} \input{variation_precision.pstex_t}\end{center}\end{figure}$

La fonction $f_{vitesse}$ détermine comment on doit interpréter les variations de la précision (cf. figure 6.19). Cette méthodet fonctionne mais donnent des résultats médiocres pour certains types d'observation ``brutales''. Par exemple, si le marcheur court très vite vers la prairie, les niveaux de détails n'auront pas le temps de s'adapter. Pour éviter ce genre de problème, un mécanisme de détection de discontinuité est mis en place : si la précision varie plus qu'un certain seuil, on revient l'espace d'un pas de temps vers une maturité synchrone.

6.2.3 Bilan

Nous verrons tout d'abord dans ce bilan comment la maturité pourrait être étendue pour assurer la prise en charge de contraintes plus complexes. Ensuite, nous dresserons un bilan de la précision et conclurons en affichant Dynamic Graph comme un véritable laboratoire perceptuel dédié à la multi-échelle.

6.2.3.1 Maturité : une variable réactive

Peut être qu'il existe une fonction de maturité valide pour tous les types d'observations. Mais peut-être sommes-nous là aussi victimes de la loi du cas particulier. En fait, il semblerait que chaque générateur d'amplifieurs nécessite une fonction personnalisée qui dépend de la manière dont on l'observe, de son type d'animation.

On peut considérer la maturité comme une variable réactive, c'est-à-dire une variable dont la valeur dépend des valeurs précédentes. Dynamic Graph propose différentes fonctions par défaut que le créateur peut choisir selon le générateur d'amplifieurs modélisé.

Mais surtout, la connaissance des pas de temps précédents permet au créateur d'écrire ses propres variables réactives. On peut imaginer, par exemple, des amplifieurs dont la maturité doit fuir certaines valeurs $v_i \in [0,1]$ pour lesquelles le résultat n'est graphiquement pas de bonne qualité.

La fonction de maturité pourrait à la limite être conçue comme le résultat d'une ``simulation physique'' complexe dont les forces tendraient à minimiser les désagréments de l'affichage. La connaissance des valeurs au pas de temps précédent font de Dynamic Graph l'outil idéal pour réaliser ce genre de simulation dans un monde procédural généré à la volée.

6.2.3.2 Plus sur la précision

La précision utilisée dans Dynamic Graph joue parfaitement son rôle : via une simple calibration visuelle pour déterminer un bon $C_{cr\acute{e}ateur}$ , un critère d'arrêt automatique libère le créateur de tâches fastidieuses. La maturité met à la disposition de ce dernier un moyen simple de réaliser des interpolations durant l'ajout de détails et peut être configurée de différentes manières (synchrone, asynchrone).

Remarquons aussi que la précision caractérise ici tout l'amplifieur. Pourtant, on peut très bien imaginer un amplifieur complexe au sein duquel la précision varie de manière non-uniforme. Par exemple, un amplifieur peut représenter un terrain multi-résolution, auquel cas sa précision varie entre les parties proches et l'horizon. Plus généralement, Dynamic Graph implique une décomposition hiérarchique des amplifieurs et ne propose aucune facilité pour les structures continues telles qu'un tronc d'arbre (1D), un terrain (2D) ou du brouillard (3D). Nous discuterons de ces limitations dans le chapitre suivant et montrerons comment Dynamic Graph supporte aussi (mais moins bien) ces structures.

6.2.3.3 Dynamic Graph : un ``laboratoire perceptuel''

Dynamic Graph, dans sa forme actuelle, ne résout pas les nombreux problèmes perceptuels posés par la synthèse d'image et la multi-échelle en particulier. Certes, le travail effectué sur la maturité apporte quelques éléments de réponse et évite notamment les états intermédiaires. Néanmoins, de nombreux critères n'ont pas été pris en compte : la vitesse des objets, leur importances dans la scène, l'influence du frame-rate, l'excentricité... Pour plus de précision sur ces critères, veuillez consulter l'excellent mémoire de thèse réalisé par Martin Reddy : Perceptually Modulated Level of Detail for Virtual Environnments dont certains éléments ont été repris dans le livre Level of Detail for 3D graphics [LRC⁺02].

J'aimerais présenter ici Dynamic Graph comme un ``laboratoire perceptuel''. En effet, Dynamic Graph offre un champ d'étude perceptuel très complet et offre une très grande souplesse. En dehors du coeur algorithmique (les arbres d'évaluations), la quasi-totalité des fonctionnalités proposées par défaut sont redéfinissables en C++ lors de la création d'un modèle. Les vitesses et les accélérations des objets sont facilement calculables grâce au tampon d'arbres. La sémantique très forte apportée par la modélisation procédurale permet l'utilisation de critère cognitif. Enfin, les possibilités d'animation et les grandes variations d'échelle permettent la création de cadres d'expérimentations très variés.

6.3 Visibilité

La visibilité est, avec la précision, un critère d'arrêt essentiel dans la génération de l'arbre d'évaluation de Dynamic Graph. Nous exposerons tout d'abord le contexte scientifique puis un algorithme original de détection d'objet caché. Nous présenterons ensuite l'algorithme puis détaillerons la plus grande difficulté de sa mise en oeuvre : assurer un parallélisme efficace entre la carte graphique et le processeur central. Nous conclurons ensuite en insistant sur le rôle essentiel de la carte graphique dans cet algorithme.

6.3.1 Présentation

Avant de décrire le contexte scientifique, je justifierai la présence de cette méthode de détection d'occultation dans ce mémoire portant sur la multi-échelle, et non la visibilité. Notamment, nous verrons comment un triple concours de circonstances favorables ``m'a interdit'' de ne pas implémenter cet algorithme. Ensuite, nous comparerons rapidement ce travail à l'existant par l'étude bibliographique [COCSD03]. Nous énumérerons ensuite les différents travaux portants sur la visibilité et la multi-échelle.

6.3.1.1 Hors-sujet?

La présence de cet algorithme dans cette thèse peut laisser perplexe. En effet, pourquoi parler de visibilité dans un travail sur la multi-échelle? Au premier regard, cela peut paraître tout simplement hors-sujet. Pourtant, la visibilité et la multi-échelle sont toutes deux motivées par un même but : «n'afficher que ce que l'on voit».

Néanmoins, bien que mues par le même désir, les techniques mises en $\oe$ uvres dans ces deux méthodes sont radicalement différentes. En fait, l'implémentation de l'algorithme de détection d'occultation de Dynamic Graph est le fruit d'un concours de trois circonstances favorables. De ce coup de chance est né un algorithme simple et efficace permettant un calcul de visibilité temps-réel sur des scènes complexes et animées.

6.3.1.2 Un coup de chance

La première circonstance favorable est le besoin. La principale raison pour laquelle Dynamic Graph nécessite un algorithme de détection d'occultation est son efficacité. Sur certaines scènes très complexes (comme le cube de Sirpienski), $80\%$ des objets dessinés par un algorithme de base n'étaient pas visibles.

La seconde circonstance est l'apparition d'une nouvelle extension sur les nouvelles cartes graphiques : GL_ARB_occlusion_query . Cette extension s'est démocratisée en 2002 et elle est désormais sur toutes les cartes graphiques. Elle permet de compter le nombre de pixels qui atteignent l'écran^6.3. L'une des applications immédiates de cette extension est un calcul de détection d'occultation (ou calcul de visibilité) : lorsque le nombre de pixels allumés par un objet vaut zéro, ce dernier n'est pas visible. On peut donc l'ignorer puisqu'il ne contribuera pas à l'image finale.

La troisième circonstance favorable est l'utilisation de la modélisation procédurale multi-échelle. En effet, tout était prêt, dans Dynamic Graph, à accueillir l'algorithme de visibilité décrit plus loin. Les boîtes englobantes hiérarchiques étaient déjà utilisées pour le calcul de précision et le view frustrum culling. L'absence de précalcul, imposée par la modélisation procédurale, montrait presque la solution du doigt... Je ne pouvais pas ne pas implémenter cet algorithme.

6.3.1.3 Contexte

Pour un état de l'art exhaustif sur le problème de la visibilité, je vous renvoie à la thèse de Frédo Durand [Dur99]. Plus récemment, une excellente étude bibliographique [COCSD03] recense de très nombreuses méthodes. Surtout, elle propose une taxonomie très précise permettant une rapide et précise description des différents algorithmes de visibilité (section 2 : Classification).

Selon cette taxonomie, voici une description de l'algorithme implémenté dans Dynamic Graph :

6.3.1.4 Visibilité et multi-échelle

Un dernier critère manque peut-être à l'appel : l'utilisation de méthodes multi-échelles. En effet, certains travaux se démarquent par l'utilisation simultanée d'un algorithme de visibilité et d'une méthode multi-échelle. À notre connaissance, la totalité d'entre eux est basée sur des méthodes de simplification hiérarchique [YSM03,ESSS01,GLY⁺03,ISGM02,ACW⁺99]. Les précalculs effectués limitent ou interdisent l'animation. En effet, lorsque le modèle change trop, il faut remettre à jour la hiérarchie.

Dans la catégorie des algorithmes alliant visibilité et multi-échelle, mon travail est le premier utilisant une approche procédurale par complexification. Par conséquent, compte tenu de l'aspect dynamique de cette approche, il est aussi le premier à permettre une animation massive, en ce sens que tous les niveaux de la hiérarchie peuvent être animés.

6.3.2 Algorithme

Sont expliquées ici les grandes lignes de cet algorithme de détection de face cachée. Celui-ci est basé sur la fonction GL_ARB_occlusion_query permettant de compter les pixels allumés par la boite englobante de la forme contenu dans un amplifieur. Avec un rendu de l'avant vers l'arrière, il est alors possible de déterminer quel objet est au moins partiellement visible. Ensuite, nous verrons pourquoi et comment limiter le nombre d'appels à la fonction GL_ARB_occlusion_query .

6.3.2.1 Calcul du nombre de pixels allumés

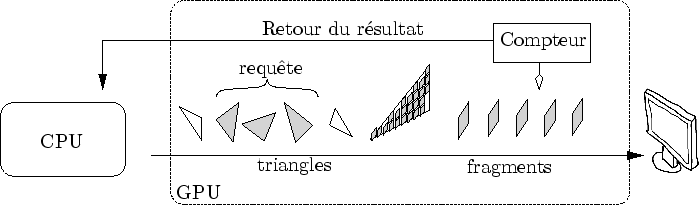
La fonction GL_ARB_occlusion_query n'est en fait qu'un simple compteur de fragments non rejetés (cf. figure 6.20). Le début et la fin du compte sont spécifiés par des commandes OpenGL s'insérant dans le flux d'information qui part vers la carte graphique. Le compteur est situé après le depth test.

**Figure 6.20:** Le CPU envoie au GPU des primitives graphiques qui sont décomposées en fragment. Un compteur compte ces derniers et renvoie le résultat au CPU. Le problème de l'asynchronicité souhaitée vient du fait que le CPU rester bloquer pendant que la requête traverse toute le pipe-line de la carte graphique et lui revienne.
$\begin{figure}\begin{center} \input{occfrag.pstex_t}\end{center}\end{figure}$

Lorsque l'on affiche un objet en l'entourant de commandes de début et de fin de requête^6.4, la fonction
GL_ARB_occlusion_query compte le nombre de pixels qui s'allument. Si l'on prend soin de désactiver l'écriture dans le tampon de couleur et de profondeur, il est possible de réaliser ce test sans influencer l'affichage.

En affichant la boîte englobante d'un objet, on obtient une borne supérieure du nombre de pixels qu'aurait affiché cet objet. L'utilisation de boîtes englobantes entraîne donc une perte de précision, mais aussi un gain de rapidité. En effet, celles-ci sont plus grossières et donc beaucoup plus rapides à afficher que les objets qu'elles englobent. De plus, dans Dynamic Graph, rappelons-le, on ne connaît même pas l'objet que l'on va afficher : celui-ci dépend de la précision.

6.3.2.2 Rendu de l'avant vers l'arrière

**Figure 6.21:** Dynamic Graph trie les amplifieurs de l'avant vers l'arrière lors de l'affichage.
$\begin{figure}\begin{center} \input{front2back.pstex_t}\end{center}\end{figure}$

La fonction GL_ARB_occlusion_query nous donne un moyen de calculer une sur-estimation de la surface réellement affichée de l'objet occulté. Pour avoir un algorithme conservatif, il faut que l'obstacle utilisé soit en quelque sorte une sous-estimation de l'obstacle réel. Dans notre cas, l'obstacle est le Z-buffer. Celui-ci, durant tout son remplissage, est une sous-estimation du Z-buffer final obtenu à la fin de l'affichage.

L'idéal serait de lancer les requêtes de visibilité sur le Z-buffer final. Ceci est malheureusement impossible car on ne peut remplir un Z-buffer qu'en évaluant la scène. Or, le calcul de visibilité est justement nécessaire à l'évaluation de cette scène : le problème ``se mord la queue''. On pourrait imaginer utiliser le Z-buffer au pas de temps précédent. Celui-ci est effectivement souvent une bonne approximation de la valeur courante. Malheureusement, assurer un calcul conservatif dans ces conditions est très difficile^6.5.

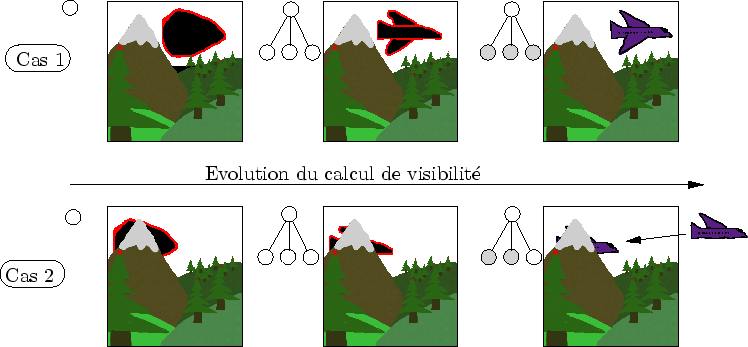
Afin de permettre un calcul de la visibilité en même temps que le calcul de la scène, celle-ci est rendue de l'avant vers l'arrière grâce à un parcours adéquat (cf. figure 6.21 et 5.9). Le but du jeu est de remplir le Z-buffer aussi vite que possible avec des valeurs aussi proches de la caméra que possible. De cette façon, le Z-buffer sera un occluder de bon qualité (i.e qui cachera le plus de chose possible). Avant d'enrichir un amplifieur, sa boîte englobante sera testée sur le Z-buffer courant (cf. figure 6.22). Les fils ne seront générés que si le nombre de pixels allumés par la boîte englobante n'est pas nul.

**Figure 6.22:** Les tests de visibilité s'effectuent sur une scène déjà partiellement dessinée. Avant de continuer l'amplification d'un objet, on teste la visibilité de sa boîte englobante. Si celle-ci est visible, l'amplification continue, sinon elle s'arrête. Lorsque la précision d'un amplifieur visible est suffisante, celui-ci est affiché.
$\begin{figure}\begin{center} \input{occtest.pstex_t}\end{center}\end{figure}$

6.3.2.3 Limitation du nombre d'appels à GL_ARB_occlusion_query

Lors de l'évaluation d'un amplifieur, le générateur peut évaluer les fonctions draw ou drawBoundingBox (ou les deux). Le but de l'organiseur est ici assez complexe : il doit bien sûr minimiser le nombre d'appels à la fonction draw. Pour cela, il va utiliser les fonctions drawBoundingBox qui, via une utilisation de GL_ARB_occlusion_query , détecte si l'amplifieur est occulté.

Mais il doit aussi minimiser le nombre d'appel à la fonction drawBoundingBox, notamment très coûteuse au niveau du taux de remplissage. Le problème ressemble à une minimisation (cf. figure 6.23). Une façon d'aborder ce problème est de donner une valeur de pertinence aux requêtes de visibilité dans le but d'en ignorer certaines. Remarquons que, conservativité oblige, tout requête non pertinente est considérée comme positive : l'objet est par défaut visible.

**Figure 6.23:** Comme toute méthode d'optimisation basée sur des tests, il faut s'assurer que le coût de ces derniers ne soit pas au bout du compte nuisible aux performances. En d'autres termes, il faut s'assurer que le test ne coûte pas plus cher que ce qu'il permet d'économiser.
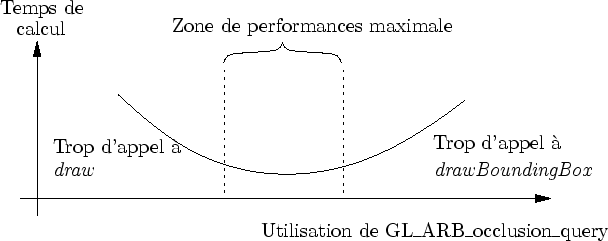$\begin{figure}\begin{center} \input{occmin.pstex_t}\end{center}\end{figure}$

Ces critères sont combinés pour former une heuristique décidant si la requête doit être lancée ou non. Une analyse précise n'a pas été réalisée et très clairement, cette heuristique est très perfectible. Actuellement, une somme pondérée de ces critères, avec des coefficients choisis empiriquement, est comparée à un seuil : le test de visibilité n'est réalisé que si la pertinence est suffisante.

6.3.3 Parallélisme GPU/CPU

La subtilité majeure de l'algorithme présenté ici est d'assurer une bonne assynchronisation entre la carte graphique et le processeur central. Nous verrons tout d'abord pourquoi une approche naïve nuit fatalement aux performances. Ensuite, nous énumérerons les moyens existants de synchronisation entre le CPU et le GPU. Enfin, nous détaillerons la mise en oeuvre du parallélisme et discuterons des auto-occultations.

6.3.3.1 Utilisation naïve

L'utilisation de GL_ARB_occlusion_query requiert quelques précautions d'utilisation. En effet, imaginons une utilisation naïve d'une requête de visibilité :

Cette approche est à proscrire. En effet, si l'utilisateur demande le résultat de la requête juste après l'avoir effectuée, il forcera la géométrie de la boîte englobante à traverser tout le pipe-line sans que celui-ci pourrait continuer à se remplir. La carte graphique se videra pendant que le processeur attend sans rien faire. Le temps moyen de traversée de la carte est non négligeable^6.6. En conséquence, il n'est pas tolérable de laisser inactif le GPU et le CPU à chaque requête de visibilité.

6.3.3.2 Moyen de synchronisation

Si l'on compare le CPU avec un énorme carrefour complexe et très fréquenté, le GPU est une autoroute à sens unique. Suivant cette métaphore, l'utilisation naïve décrite plus haut revient à laisser entrer quelques voitures sur l'autoroute, puis à la fermer et à attendre que les voitures arrivent à destination avant de la rouvrir. L'accumulation de voitures à l'entrée de l'autoroute paralyserait complètement le grand échangeur (le CPU), contraint d'attendre sans bouger que l'autoroute soit de nouveau ouverte.

Il existe actuellement trois moyens pour contrôler la synchronisation entre un CPU et la carte graphique :

L'utilisation de glFinish est à proscrire (le CPU et le GPU attendent). L'utilisation des
GL_NV_fence est prometteuse mais n'a pas été étudiée ici. La solution choisie consiste à utiliser glFlush couplé à une estimation du temps de traversée du GPU.

6.3.3.3 Mise en $\oe$ uvre du parallélisme

Pour remédier au temps perdu par une utilisation naïve, il convient avant tout de toujours envoyer de nouvelles informations au GPU. Pour cela, il est absolument nécessaire de ne pas demander le résultat de la requête de visibilité juste après l'avoir exécuté par un glFlush. Chaque amplifieur en attente devient alors bloquant, c'est-à-dire que le générateur ne peut plus les visiter avant que le résultat des requêtes soient disponibles. Si éventuellement tous les noeuds sont bloquants, alors la seule solution est d'attendre que les réponses des requêtes soient disponibles.

De plus, il n'est pas conseillé d'appeler glFlush trop souvent car le bus aime bien les gros paquets d'informations. Il faut donc envoyer des groupes de requêtes. La taille des groupes ne doit pas être trop grande, sans quoi tous les noeuds risquent de devenir bloquants. Cette situation arrive parfois en début de création de graphe lorsque les choix sont peu nombreux. C'est une raison de plus pour développer les tous premiers niveaux du graphe sans tester la visibilité.

Dans Dynamic Graph, le CPU utilise le générateur pour visiter les noeuds non bloquants pendant que le GPU calcule les requêtes de visibilité. Les réponses, une fois rapatriées sur le CPU, vont débloquer les noeuds bloquants et le générateur pourra alors les visiter.

6.3.3.4 Auto-occultation

Mais le problème ne s'arrête pas là. Il est nécessaire de limiter les auto-occultations au sein d'un même groupe de requêtes. Afin d'illustrer cette nécessité, penchons nous sur l'exemple suivant : le visiteur laisse les noeuds A et B en attente le temps que leur calcul de visibilité se termine. Pendant ce calcul, A et B n'influent pas sur le Z-buffer (grâce à glDepthMask) mais comptent juste le nombre de pixels qu'allument leurs bounding-box. Que se passe-t-il si A occulte complètement B? Comme les visibilités de A et B sont évaluées en même temps, cette occultation ne sera pas détectée, amenant des calculs inutiles (mais conservativement sans risque).

Il est donc nécessaire de bien répartir les membres d'un groupe de requêtes de visibilité selon leur placement sur l'écran. Idéalement, si les membres sont mutuellement non-recouvrants, le test de visibilité sera optimal. En pratique, il serait trop coûteux d'assurer cette condition et il est suffisant de bien répartir les requêtes sur l'écran pour obtenir de bonne performance. Cette répartition est actuellement implicitement et partiellement réalisé par le tri en profondeur. Cette méthode simpliste devrait pouvoir être améliorer par une meilleur connaissance de la répartition des boîtes englobantes sur le plan de l'image.

6.3.4 Bilan

Nous décrirons tout d'abord les répercussions importantes de cet algorithme sur l'architecture de Dynamic Graph. D'un point de vue plus abstrait, nous décrirons la carte graphique comme l'observateur du monde virtuel contenu dans les modèles de Dynamic Graph. Plus concrètement, nous discuterons rapidement des performances. Enfin, nous ajouterons une note sur l'utilisation de la transparence avec cet algorithme de visibilité.

6.3.4.1 Un pipe-line complexe

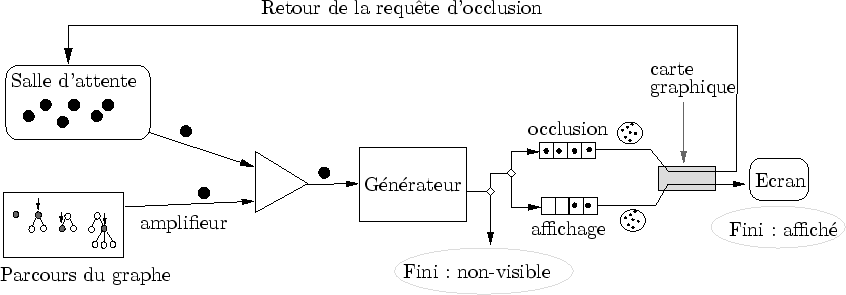
Au bout du compte, les contraintes qu'entraîne le parallélisme entre le processeur central et la carte graphique compliquent notablement le pipe-line d'évaluation. Sans rentrer dans les détails, la figure 6.24 donne un aperçu simplifié de la structure utilisée. Le rôle de la salle d'attente est essentiel : elle permet aux amplifieurs d'attendre sagement que leur requête de visibilité soit terminée.

**Figure 6.24:** Afin d'assurer un parallélisme efficace entre le GPU et le CPU, la génération de l'arbre d'évaluation est jalonnée de files d'attente. Notamment, les files d'attentes de l'affichage et de l'occultation ont pour premier objectif de grouper les commandes OpenGL. De plus, la file d'attente de l'affichage applique un tri local d'avant vers l'arrière pour compléter le tri réalisé lors du parcours du graphe.
$\begin{figure}\begin{center} \input{pipe.pstex_t}\end{center}\end{figure}$

6.3.4.2 La carte graphique observe le modèle

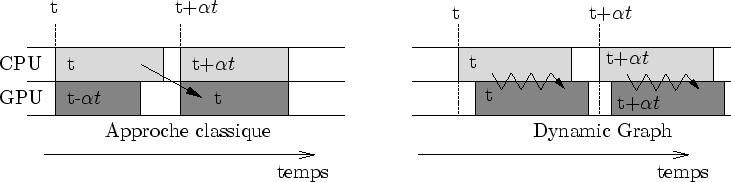
Fondamentalement, l'algorithme de rendu de Dynamic Graph est l'esclave de la carte graphique (cf. figure 6.25). Ceci diffère radicalement des approches pour lesquelles on envoie toutes les informations d'un bloc. Ici, l'algorithme de détection d'occultation amène un échange plus complexe.

**Figure 6.25:** L'échange complexe que Dynamic Graph fait avec la carte graphique permet d'afficher un modèle en même temps qu'il est animé (évalué). Plus classiquement, les méthodes d'animation affichent usuellement le résultat d'une animation au pas de temps suivant. De ce point de vue, notre approche réduit la latence [LRC⁺02] de l'affichage.
$\begin{figure}\begin{center} \input{gpu_cpu.pstex_t}\end{center}\end{figure}$

Cette évolution est en fait très naturelle. Rappelons que c'est l'observateur qui limite la génération de l'arbre d'évaluation par des critères de visibilité et de précision. Ne pourrait on pas considérer que la carte graphique est cet observateur ? C'est en quelque sorte elle qui observe les données virtuelles du modèle. On peut représenter la carte graphique comme un $\oe$ il intermédiaire (dont l'écran est la rétine) entre le modèle et le créateur. Il est tout naturel que Dynamic Graph interroge la carte graphique pour lui demander son avis : "vous en voulez encore ou on s'arrête là?". D'ailleurs, il est probable que le calcul de précision ou de view frutrum culling bénéficie aussi un jour des avantages de l'accélération matérielle par un retour de l'information du GPU vers le CPU.

6.3.4.3 Performance

Les résultats sont graphiquement corrects, ce qui est tout à fait normal puisque l'algorithme est conservatif. La figure 6.26 donne un aperçu des résultats grâce à une seconde caméra.

**Figure 6.26:** Sous différents angles, on apprécie la quantité d'informations supprimées.
$\begin{figure}\begin{center} \input{occ.pstex_t}\end{center}\end{figure}$

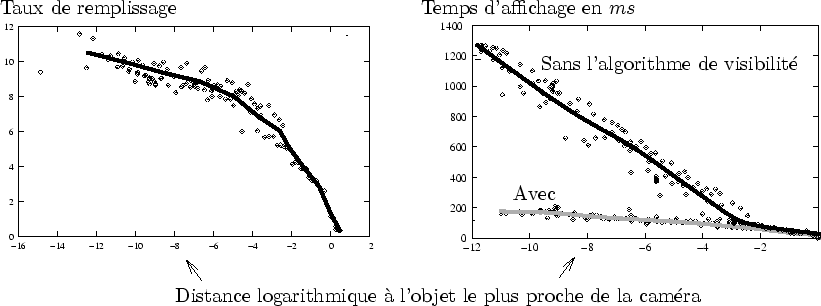
Dans le cas du cube de Sirpienski, une mesure du taux de remplissage a été effectuée (cf. figure 6.27). Le taux de remplissage mesure le nombre de fragments passant nécessaire au rendu final. Dans un cas idéal, un seul fragment serait envoyé par pixel. Mais ce chiffre n'est jamais égalé notamment parce qu'un grand nombre de fragments inutils doit être produit pour obtenir le résultat final. Au final, on peut mesurer le nombre total de fragments générés en équivalent écrans. Par exemple, un taux de remplissage égal à $12 \acute{e}crans$ signifie que l'équivalent de

écrans a été rempli par les fragments durant un affichage.

Le taux de remplissage engendré par l'affichage lui-même est très stable et reste entre $2 \acute{e}crans$ et $5 \acute{e}crans$ (cette valeur dépend beaucoup du modèle). Lorsque la caméra est très proche du cube, le taux de remplissage engendré par les boîtes englobantes monte jusqu'à $12 \acute{e}crans$ . Au total, le taux de remplissage est monté jusqu'à $17 \acute{e}crans$ pour une observation très proche. Sans l'algorithme de détection d'occultation, dans les même conditions, le taux de remplissage vaut $200 \acute{e}crans$ (soit un facteur

) !! Clairement, le jeu en vaut la chandelle.

Néanmoins, un taux de remplissage de

peut être jugé trop élevé. Nous estimons que les heuristiques utilisées pour décider de l'exécution ou non du test de détection d'occultation sont actuellement très basiques. Une étude plus poussée améliorerait sans aucun doute ces résultats.

Le plus surprenant vient du fait que, d'une part, ce taux de remplissage énorme ne nuit pas à un affichage interactif. Ceci est certainement dû au fait que l'affichage des boîtes englobantes et très élémentaire (aucun éclairage, géométrie grossière). Il est possible que des techniques de early Z test (cf. [WW03]) accélèrent très sensiblement les calculs. De plus, il est clair que la puissance des cartes graphiques actuelles joue un rôle décisif.

Les performances de cet algorithme dépendent du type de scène affiché. Actuellement, seul une dizaine de modèles relativement simples ont été réalisés. Pour chacun d'eux, le gain est évident. Il est difficile de prédire les résultats dans le cas général. Il est pourtant clair que plus le taux de remplissage de la scène est grand, plus les performances seront bonnes. Par conséquent, plus la scène est complexe et volumique, plus le gain sera marqué. Quant à la comparaison de cet algorithme avec les algorithmes existants, le constat est simple : plus la scène affichée sera vaste, précise, chaotique et animée, plus l'algorithme présenté ici montrera sa supériorité.

**Figure 6.27:** Les mesures sont effectuées en fonction de l'échelle d'observation (plus précisément, en fonction de la distance à l'objet le plus proche). Le modèle utilisé est le cube de Sirpienski. À gauche, la courbe représente le taux de remplissage engendrée par *les boîtes englobantes uniquement*. À droite, des mesure du *frame-rate* avec et sans l'algorithme de visibilité ont été effectuées.
$\begin{figure}\begin{center} \input{occ_mesure.pstex_t}\end{center}\end{figure}$

6.3.4.4 Transparence

La transparence n'est actuellement pas permise en même temps que l'utilisation de l'algorithme de visibilité. Cela est dû au fait qu'il est actuellement impossible de mettre à jour le Z-buffer en utilisant la fonction glBlendFunc avec un rendu de l'avant vers l'arrière. Suite à une discussion avec Fabrice Neyret, il semblerait qu'une extension très simple puisse remédier à ce problème. Il suffirait d'ajouter une nouvelle sorte de test $\alpha$ du type :

La valeur $A_{threshhold}$ détermine la valeur à partir de laquelle on considère le pixel comme opaque. Cette extension est simple et prometteuse mais reste à être implémenter en hardware.

6.4 Bilan

Les entrailles de la bête sont désormais connues, voyons comment on peut la dompter.

6.4.0.1 Une structure souple, dynamique et performante

Dynamic Graph offre une structure très dynamique régénérée à chaque pas de temps. Néanmoins, contrairement à la plupart des méthodes procédurales ``à la volée'', des mécanismes permettent d'accéder aux valeurs des pas de temps précédent.

La forme affichée est une fonction de l'observateur, en perpétuelle adaptation aux variations de ce dernier. Des critères de précision et de visibilité assurent que seule l'information nécessaire à l'observation est générée.

La structure en pipe-line de la carte graphique influe notablement l'architecture de Dynamic Graph. Des méthodes de parallélisme dédiées permettent au processeur central d'utiliser la puissance de ces dernières sans pour autant nuire aux performances.

6.4.0.2 Vers la modélisation

Il peut paraître un peu ambitieux de proposer une solution recouvrant tout le processus de création. Généralement, un travail de recherche est plus local et s'attarde exclusivement sur la modélisation ou l'animation ou le rendu, mais pas sur tous ces domaines à la fois !

Tout d'abord, précisons que le processus de création que j'ai développé dans Dynamic Graph est très simpliste. Notamment, comme nous le verrons bientôt, la phase de modélisation est réalisée essentiellement par une interface textuelle. J'aimerais préciser aussi que j'aurais aimer me raccrocher à des outils existants. Mais l'originalité du langage descriptif de Dynamic Graph impose, en amont et en aval du processus de création, des outils très spécifiques. Nous venons de voir les particularités de l'algorithme de rendu (en aval). Voyons maintenant les particularités de l'algorithme de modélisation (en amont).

Dynamic Graph propose une représentation plus fondamentale dans laquelle l'affichage ne joue finalement qu'un second rôle. La modélisation revient essentiellement à décrire le modèle de façon minimaliste par des paramètres pertinents : plutôt que la surface, c'est le ``squelette'' qui est décrit. Le créateur manipule ensuite ces paramètres pour les animer ou les rendre plus précis.

Voyons maintenant, dans le chapitre suivant, comment aborder cette modélisation complexe.